Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

232 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

Turbulent core

Buffer layer

Viscous sublayer

Laminar

Transition

Turbulent

)

(y)

)

(y)

(r)

Fully DevelopedEntrance Length

)

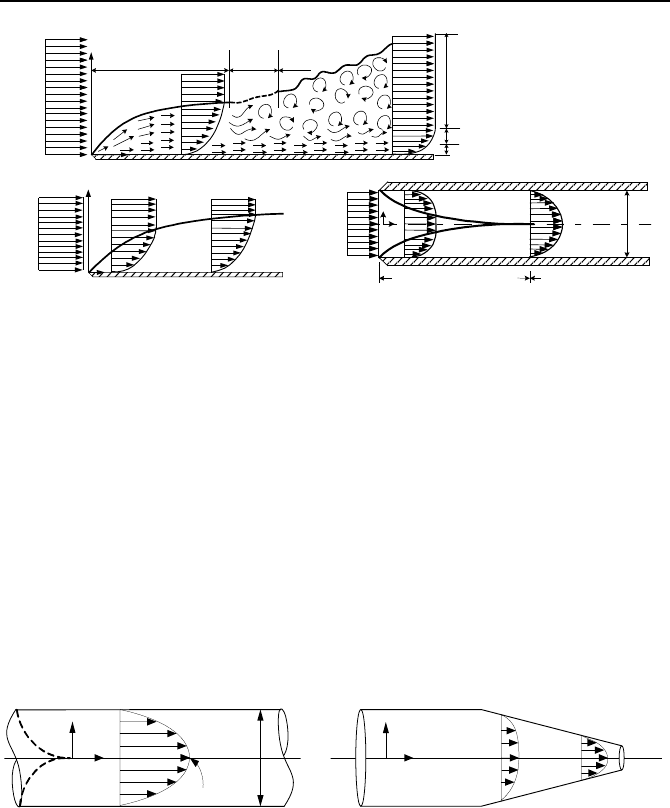
Figure IIIa.1.6. Comparison of boundary layers over a flat plate and in a pipe

Thickness of the boundary layer over a flat plate is a function of the distance

from the leading edge and the Reynolds number. For example, for flow of air

over a flat plate at 2 m/s and 27 C, the boundary layer thickness at 0.5 m from the

leading edge is about 1 cm or 0.4 in.

Flow dimensions refer to the number of velocity components in a given coor-

dinate system. Fluid flow, in general, is three-dimensional such as the plume from

a cooling tower. However, in some applications, flow may be considered two or

even one-dimensional, which greatly simplifies analysis. An example for the one-

dimensional flow includes the fully developed region of viscous flows in a pipe as

shown in Figure IIIa.1.7(a). Figure IIIa.1.7(b) shows the two-dimensional flow of

a viscous fluid in a nozzle (variable flow area). Another example for a two-

dimensional flow includes the developing flow of viscous flows in the entrance

region of a pipe.

=f (r,x)

=f (r)

)

max

(a) (b)

Figure IIIa.1.7. Examples of (a) one-dimensional and (b) two-dimensional flow

External and internal flows refer to conditions where a solid boundary is im-

mersed in the flow or contains the flow, respectively. Analysis of external flow is

essential for such engineering applications as tube banks, airfoils, ship hull, or

blunt bodies. Lift and drag are phenomena pertinent to external flow. Analysis of

internal flow is essential for such engineering applications as flow of fluids in

pipelines, pumps, turbines, and compressors.

2. Fluid Kinematics 233

Separation point

Boundary layer

Wake

(a) (b)

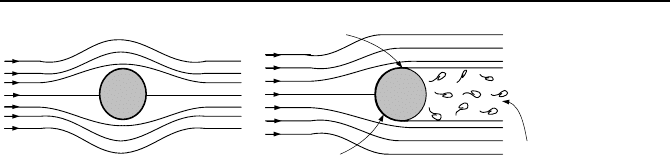
Figure IIIa.1.8. External flow over cylinder (a) ideal flow and (b) real flow

Shown in Figure IIIa.1.8 is a cylinder exposed first to an ideal flow and then to

a real flow. In either case, the flow far from the body can be considered ideal,

even in the case of the real flow. This is because far away from the cylinder, fric-

tion in the real flow is negligible especially for low velocity flow. As the flow ap-

proaches the cylinder (in the case of an ideal flow) the streamlines are squeezed to

accommodate the cylinder and there is no friction. In the case of real flow, the

boundary layer is developed in which flow velocity at the wall is zero. The veloc-

ity profile inside the boundary layer depends on the flow Reynolds number (i.e.,

laminar or turbulent). For ideal flow, the streamlines recover downstream of the

cylinder to produce a symmetric pattern. Hence, pressures upstream and down-

stream of the cylinder are equal (i.e. there is no drag acting on the cylinder). This

did not conform to the results obtained in experiments. Therefore, in the early

days of fluid dynamics, this phenomenon was known as the d’Alembert’s Para-

dox. With the introduction of the boundary layer by Prandtl in 1904, the existence

of drag in real fluids was confirmed and the paradox resolved. Division of the

flow by Prandtl into two regions of free stream with negligible friction and bound-

ary layer where frictional effects are important is one of the most important con-

tributions to the field of fluid mechanics.

Boundary layer separation. In real fluids, as flow passes the cylinder, there is

a region in which a fluid particle moving in the boundary layer lacks sufficient ki-

netic energy to convert to enthalpy. The particle cannot then move into the

higher-pressure region and the external pressure causes the particle to move in the

opposite direction of the velocity profile. When this happens, separation of the

boundary layer ensues. A vortex created as the result of this reverse flow is even-

tually detached from the surface to drift downstream of the cylinder to produce a

turbulent wake behind the cylinder. This leads to the appearance of a wake behind

the cylinder. The subsequent pressure drop gives rise to a drag acting on the cyl-

inder. To reduce drag, the object must be streamlined. That is to say that if the

cylinder is replaced with an airfoil, the gradual tapering of the trailing edge pre-

vents separation of the boundary layer to a large extent, which then substantially

reduces drag.

2. Fluid Kinematics

Earlier we defined the continuum hypothesis, allowing us to treat a fluid as a con-

tinuous matter and using such terms as fluid element and fluid particle. We shall

234 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

use this hypothesis to derive the conservation equations of mass, momentum, and

energy. However, before we embark on the derivation, we need to define the

frame of reference. In fluid mechanics, there are two frameworks. A flow field

can either be described based on the motion of a specific fluid element or the mo-

tion of the fluid through a specific region in space. These frameworks are referred

to as Lagrangian and Eulerian descriptions, respectively. In the Lagrangian ap-

proach, the trajectory of an individual particle is followed. In the Eulerian ap-

proach, the flow at every fixed point as a function of time is described. These

frameworks are further described in the context of acceleration for a fluid element.

2.1. Fluid Acceleration

Prior to studying the dynamics of the fluid flow, we begin by deriving the accel-

eration of a fluid element in a flow field. Other aspects of fluid kinematics, such

as fluid rotation, are discussed later in this chapter. The velocity of an infinitesi-

mal fluid element in the Cartesian coordinate system based on the Eulerian

descrption is expressed as:

kttztytxVjttztytxVittztytxVtrV

zyx

]),(),(),([]),(),(),([]),(),(),([),( ++=

IIIa.2.1

In Equation IIIa.2.1

kji

and,, are the unit vectors of Cartesian coordinates. Also

x, y, z, and t are four variables representing space and time. Finally, V

, V

, and

are the components of the velocity vector in the x, y, and z directions, respec-

tively. In Figure IIIa.2.1, vector

),( trV

represents the velocity of a fluid element

at location

at time t, while vector ),( dttrdrV ++

represents the velocity of the

same fluid element, which has moved in time dt by

. According to the La-

grangian approach, the acceleration of the fluid element is given by

dtVda /

= .

Using the chain rule for differentiation (Chapter VIIa):

∂

IIIa.2.2

Fluid element

at time t

The same fluid element

but at t + dt and r + dr

V(r, t)

V(r, t) dV

V(r + dr, t + dt)

Figure IIIa.2.1. Velocity of a fluid element in Cartesian coordinates

By substituting for

Vdtdx =/ ,

Vdtdy =/ , and

Vdtdz =/ , Equation IIIa.2.2

can be rearranged to obtain:

2. Fluid Kinematics 235

∂

zyx

IIIa.2.3

Equation IIIa.2.3 is a vector equation. Therefore, it has three components for

kajaiaa

zyx

++= . Also the term in the first parenthesis represents the local

acceleration, due to the change of flow velocity with time. This is because the lo-

cal derivative (

∂/∂t), is the rate of change of a fluid flow property as seen by an

observer at a fixed position in space. Term d/dt is the total derivative.

Terms in the second parenthesis represent the convective acceleration due to

the change of flow velocity in space

. The above relation can be simplified by no-

ticing that the last three terms in the second parenthesis are dot products of the ve-

locity vector and the gradient operator (see Chapter VIIc for the definition of the

gradient operator in the three coordinate systems). Thus, in Cartesian coordinates

we write:

()

tDt

∇⋅+

∂

IIIa.2.4

Note the change of notation in the left side of Equation IIIa.2.4 from d/dt to D/Dt,

which is referred to as the substantial derivative (since one moves with the sub-

stance). Thus the substantial derivative (D/Dt) refers to the time rate of change of

a fluid flow property as viewed by an observer at the origin of the coordinate sys-

tem, which is moving at the flow velocity

. Also note that in the right-hand side

of Equation IIIa.2.4 the derivative terms are placed in a bracket. This allows us to

express the substantial derivative as a mathematical operator:

()

∇⋅+

∂

Calling the substantial derivative an operator implies that it can operate on all the

flow field properties such as pressure, temperature, velocity, density, etc. This is

described later in this section.

Example IIIa.2.1. Find the acceleration of a fluid particle in the Cartesian coor-

dinate system.

Solution: We substitute Equation IIIa.2.1 into Equation IIIa.2.3 and evaluate each

term as follows:

ijk

tt t t

∂

=++

∂∂ ∂ ∂

If the observer’s reference is accelerating then the acceleration of a particle with respect to a fixed

reference is given in Chapter VIb by Equation VIb.3.9.

236 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

∂

Summing up terms, fluid acceleration in the Cartesian coordinates may be written

as:

∂

IIIa.2.3-1

Example IIIa.2.2. Find the acceleration of a fluid particle at x = 1 cm, y = 2 cm,

and z = –1 cm at t = 3 s in a flow field with Eulerian velocity in the Cartesian co-

ordinates given as kztjyixtV

)1( −+−= cm/s.

Solution: We first note that V

= xt, V

= –y, V

= (1 – t)z. We then carry out de-

rivatives as follows:

For V

: ∂V

/∂t = x, ∂V

/∂x = t, ∂V

/∂y = 0, and ∂V

/∂z = 0.

For V

: ∂V

/∂t = 0, ∂V

/∂x = 0, ∂V

/∂y = -1, and ∂V

/∂z = 0

For V

: ∂V

/∂t = -z, ∂V

/∂x = 0, ∂V

/∂y = 0, and ∂V

/∂z = (1 – t)

Substituting into Equation IIIa.2.3-1, we obtain: ktztjyitxa

)2()1(

−+++=

cm/s

. For the specified point at the specified time, the acceleration becomes:

kjia

3210 −+= with

2222

cm/s63.10)3(210 =−++=a

Example IIIa.2.3. The flow velocity in a flow field is given as V

(x) = V

[1 –

(2x/3L)]. Find the flow acceleration of a point located at x = 0.75 m. Use L = 1 m

and V

= 3 m/s.

Solution: This is a one-dimensional, steady flow hence the local acceleration is

zero. We can find the convective acceleration from

= V

(dV

/dx) = V

[1 – (2x/3L)][–2V

/3L] = –2

V [1 – (2x/3L)]/3L

For the specified location, we find a

= –3 m/s

. The minus sign indicates that

flow decelerates.

2. Fluid Kinematics 237

We now further elaborate on the two types of accelerations defined earlier.

Let’s generalize the discussion by using a flow property c

, being a function of

both space and time

),( trfc

= where c may represent P, T, V,

, etc. Equa-

tion IIIa.2.4 for the flow property c is then written as:

()

∇⋅+

∂

IIIa.2.5

If the property

c of the flow field is being observed from a fixed point with respect

to the flow field, we show the time rate of change of property

c by the partial de-

rivative

tc ∂∂ , which we referred to as the local acceleration when c = V. An ex-

ample for the case where c represents velocity, c = V includes acceleration of

stagnant water in a constant diameter pipe when a pump is turned on. Similarly,

an example for the case that c represents temperature, c = T is when we place a

container of cold water in a warm room.

Regarding the convective acceleration, an example for c = V is when fluid

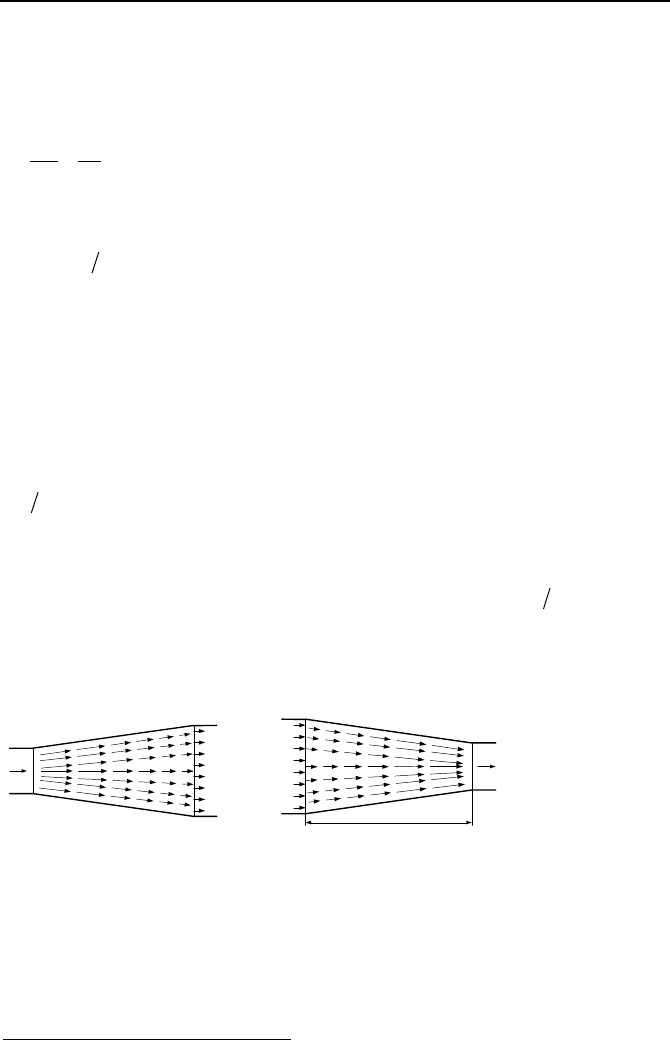
steadily flows through a converging or diverging channel as shown in Fig-

ures IIIa.2.2(a) and IIIa.2.2(b), respectively. From the point of view of a station-

ary observer, for this steady state fluid flow, velocity at any point along the chan-

nel is independent of time. Hence, according to the Eulerian approach we have

0=∂∂ tV . However, from the point of view of an observer moving with the

flow, velocity at any point along the channel is changing with time because the

flow area is changing. If the observer moves at the same velocity as the flow ve-

locity, according to the Lagrangian approach, DV/Dt is not zero

. Using the sub-

stantial derivative, Equation IIIa.2.5 for this case predicts that

(

)

VVDtDV

∇⋅= .

As a result, in Equation IIIa.2.5, the left side describes the rate of change of flow

property in the Lagrangian and the right hand sides describe the rate of change of

flow property c in the Eulerian framework.

(a) (b)

Figure IIIa.2.2. 1-D velocity vectors in a steady ideal flow field. a) decelerating flow and

b) accelerating flow

So far we discussed the case that the observer is either fixed or moves in the

flow with the same velocity as the flow velocity. But what if the observer is mov-

ing in the flow field at a velocity

, which is different than the flow velocity

Try an example in which c =

. For solution, search for “acceleration pressure drop” in

Chapters IIIb and Va.

238 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

( VV

≠ )? In this case, we use the same chain rule as given by Equation IIIa.2.2

but the derivatives of the location become the components of the observer velocity

vector:

ozoyox

∂

where we used d/dt in the left side to distinguish this case from the case that the

observer is moving at the flow velocity. This derivative is referred to as the total

time derivative. Similar to the substantial derivative, we can write the right side in

a more familiar manner:

()

tdt

∇⋅+

∂

IIIa.2.6

By canceling the partial derivative tc ∂∂ between Equations IIIa.2.5 and IIIa.2.6,

we find the relation between the total and the substantial derivatives as:

()

cVV

∇⋅−+=

IIIa.2.7

The substantial derivative is equal to the total derivative when the observer veloc-

ity is equal to the flow velocity.

The Lagrangian approach is well suited for solid mechanics where the focus is

on the motion of individual particles. The continuum hypothesis also makes the

Lagrangian approach useful for the derivation of the conservation equation in fluid

mechanics. For example, the conservation equation of mass, using the Lagrangian

framework simply becomes m = constant (Dm/Dt = 0). Similarly, the momentum

equation for fluids as given by Newton’s second law of motion has its simplest

form when written in the Lagrangian framework;

= D(mV

)/Dt. Finally, the

simplest form of the conservation equation of energy is the one written for a

closed system, using the Lagrangian description, as given by Equation IIa.6.1. As

described in the next section, we can either use the Lagrangian approach to derive

the set of conservation equations and then substitute from the Eulerian equivalent

(Equation IIIa.2.5) or directly derive the Eulerian formulation by observing flow

entering and leaving a stationary control volume (the Lagrangian free-body dia-

gram).

Example IIIa.2.4. Find the framework that, from the fluid mechanics point of

view, best describes the following situations: a) a lion chasing a deer in a herd,

b) a traffic engineer surveying the traffic pattern at an intersection, c) a bird carry-

ing a tag to study the migration pattern of a flock of birds, d) a cameraman filming

a school of fish entering and leaving a coral reef, and e) a chemist sampling river

water for pollution.

Solution: The answers are a) Lagrangian, b) Eulerian, c) Lagrangian, d) Eulerian,

and e) Eulerian.

3. Conservation Equations 239

Next, we solve an example for convective acceleration in a fluid flowing at

steady state condition.

Example IIIa.2.5. Consider the conduit shown in Figure IIIa.2.2(b). The conduit

has a width of 1 ft (3.28 m). The flow area at x = 0 is 2.5 ft

(0.23 m

) and at x = L

= 6 ft (1.83 m) is 1 ft

(0.1 m

). Fluid flows steadily at a volumetric flow rate of



= 12 ft

/s (0.34 m

/s). Find the acceleration of a point located at x = 3 ft.

Solution: To find acceleration, we first need to find velocity. Since we are given

the volumetric flow rate, we find velocity from V

= V



/A(x). The flow area be-

tween x = 0 and x = L is a function of x and can be found as A = A

+ (A

– A

)x/L.

Substituting values, we find A = 2.5 – 1.5x/L. Hence, V(x) = V



/A = 12/(2.5 –

1.5x/L). For the one-dimensional flow, V

= V

= 0 and acceleration from Equa-

tion IIIa.2.2 is found as:

∂

Since fluid flows steadily 0/ =∂∂ tV

. We find dV

/dx = (18/L)/(2.5 – 1.5x/L)

Therefore,

= [12/(2.5 – 1.5x/L)](18/L)/(2.5 – 1.5x/L) = (18/L)/(2.5 – 1.5x/L)

= (216/6)/(2.5

– 1.5/2)

= 6.72 ft/s

In the next example, we find the total acceleration due to the presence of local

and convective accelerations.

Example IIIa.2.6. Find the acceleration in Example IIIa.2.5 if the flow is increas-

ing at a rate of 2.5 ft

Solution: The convective acceleration remains the same. The local acceleration

must now be calculated from ∂V

/∂t. We found V

= V



/A(x). Thus, ∂V

/∂t =

∂[ V



/A(x)]/∂t = 2.5/A(x). At x = 3, ∂V

/∂t = 2.5/1.75 = 1.43 ft/s

. Total accelera-

tion is then found as a

= 1.43 + 6.72 = 8.15 ft/s

3. Conservation Equations

Information about a flow field can be obtained from the solution to the conserva-

tion equations, which can be derived either in an integral form for a finite control

volume or in differential form for an infinitesimal control volume. The latter ap-

proach is necessary if the goal is to obtain detailed information in the flow field

such as determination of pressure, temperature, or velocity distributions. Addi-

tionally, there is dimensional analysis. Therefore, we may say that in general,

there are three types of analyses for solving the single-phase fluid flow problems

namely, differential, integral, and dimensional. Each type of analysis has its own

benefits and drawbacks. For example, in the differential analysis, the three con-

240 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

servation equations of mass, momentum, and energy are applied to an infinitesi-

mal element of the flow field. These three differential equations are then inte-

grated over the specific region of interest with specified boundary conditions pe-

culiar to that region. The integrated equations in conjunction with the thermo-

dynamic equation of state provide sufficient number of equations to find such key

flow parameters as pressure, temperature, velocity, and density. The advantage of

the differential analysis is the detailed information it provides about the region be-

ing analyzed. This includes distribution of pressure and velocity in the flow field.

The disadvantage of this method is the intensive computational efforts required for

solving the problem. This is due to the fact that, except in special cases, analytical

solutions in closed form cannot be obtained hence, seeking numerical solutions is

inevitable. Depending on the extent of details desired, such numerical solutions,

even with today’s computational abilities, remain labor intensive and are used

only if no other method provides the required information.

In integral analysis, a control volume of finite size is assigned to the region of

interest and the three conservation equations are applied. These equations already

include the boundary conditions. The advantage of this method is the ease in set-

ting up and solving the integral equations. The obvious disadvantage is the loss of

details within the control volume. However, depending on the case being ana-

lyzed, the analyst may not require such details, average values representing the re-

gion may be quite sufficient.

Finally, in dimensional analysis we try to find relevant dimensionless parame-

ters without knowing the related differential equations. In this chapter we discuss

only the integral and the differential analyses.

3.1. Integral Analysis of Conservation Equations

This method is applied to control volumes with finite size. We take advantage of

the Lagrangian approach to set up the conservation equations and by using the

Eulerian approach, we then convert these equations to suit fluid flow applications.

Since the Lagrangian approach is applied to a closed system (an entity having a

constant mass), the Reynolds transport theorem is used to relate the rate of change

of properties of the system to that of a control volume. As was discussed in Chap-

ter IIa, if Y represents an extensive property of a system, then y represents the in-

tensive property so that y = dY/dm. According to the Reynolds transport theo-

rem

, we can write:

()

³³³³³

⋅+

∂

....

)(V

SCVC

System

SdVydy

ρρ

IIIa.3.1

where dV is the differential volume and dS is the differential surface area encom-

passing the control volume. As was discussed in Section 2, the left side in Equa-

This theorem is derived in Chapter VIIc from the general transport theorem and the Leib-

nitz rule for the differentiation of integrals. See Equation VIIc.1.31 for the Reynolds

transport theorem as applied to a fixed control volume.

3. Conservation Equations 241

tion IIIa.3.1 represents the Lagrangian definition and the right side represents the

Eulerian equivalent. We use Equation IIIa.3.1 to derive the integral form of the

conservation equations of mass, momentum, and energy as discussed next.

Conservation Equation of Mass, Integral Approach

In the case of conservation equation of mass, Y = m and y = dY/dm = 1. These can

be substituted in Equation IIIa.3.1 noting that the left side becomes zero, as the

system mass is constant:

0)( =

System

Therefore, Equation IIIa.3.1 simplifies to:

0)(V

....

=⋅+

∂

³³³³³

SCVC

SdVd

ρρ

IIIa.3.2

Equation IIIa.3.2 is the Eulerian description of the conservation equation of mass.

It expresses the fact that the rate of change of mass in a control volume is due to

the algebraic summation of mass flow rates entering and leaving the control vol-

ume. For steady state and incompressible flow, Equation IIIa.3.2 becomes:

³³

0)()()(

=−=−=⋅

¦¦¦¦

PortsInlet PortsInlet

PortsExit

ein

PortsExit

mmVAVASdV



ρρρ

IIIa.3.3

Note that for incompressible fluids at constant temperature, density remains the

same in the flow field hence, it cancels out in the above equation.

Conservation Equation of Momentum, Integral Approach

In the case of conservation equation of momentum, Y = mV and y = V. These can

be substituted in Equation IIIa.3.1 to obtain:

()

³³

⋅+

³³³

∂

....

)(V

SCVC

System

SdVVdV

KKKK

ρρ

IIIa.3.4

The left-hand side is the Lagrangian description of momentum of the system. Ac-

cording to Newton’s second law, the system momentum is related to the algebraic

summation of all forces acting on the system:

()

¦¦¦

+==

ForceSurfaceForceBody

System

FFFVm

IIIa.3.5

The conservation equation for momentum can then be written as: