Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

Questions and Problems

221

a) the atmosphere components are uniformely mixed and in thermodynamic equi-

librium,

b) air can be treated as an ideal gas,

c) no heat loss from the reactor to the drywell atmosphere,

d) no steam condensation on the drywell walls,

e) blowdown takes place at a constant reactor pressure of 500 psia (3.45 MPa) for

the duration of interest

f) no heat loss from drywell through the walls

g) steam may be treated as an ideal gas so that u

Steam

= u

+ c

v,Steam

(T – T

sat

) and

Steam

= h

+ c

p,Steam

(T – T

sat

), where u

= 1098 Btu/lbm (2554 kJ/kg), h

= 1180

Btu/lbm (2744 kJ/kg), and T

sat

= 776 R (431 K).

[Ans.: t = 89 s, P

= 70 psia, T

= 475 F (246 C),

= 12%, m

= 35,439 lbm

(16,286 kg)].

Drywell

Suppression

Pool

23.2 ft

10 ft

Duct

Rupture

Disk

Secondary

Containemnt

Break

Reactor

Vessel



Pool

Steam, air, and

nitrogen

Figure for Problem 20 Figure for Problem 21

21. A large containment is filled with steam, air, and nitrogen. The containment also has a

pool of water, which is sprayed in the containment atmosphere. Heat is added to the con-

tainment at a specified rate. Use the given data to find a) the initial containment pressure

and b) the time it takes for the containment pressure to reach the pressure limit of 145 psia

(1 MPa).

Total mass of water (water in the pool and steam) m

= 3.42E6 lbm (1.55E6 kg)

Water-steam quality x = 0.03

Air mass m

= 0.132E6 lbm (6E4 kg)

Nitrogen mass m

= 2200 lbm (998 kg)

Containment initial temperature T

= 688 R (109 C)

Initial relative humidity

= 100%

Rate of heat addition to containment atmosphere



= 1.02E8 Btu/h (30 MW)

[Ans.: 7.66 h].

III

. Fluid Mechanics

Topics in single-phase flow range from such simple phenomena as the flow of wa-

ter in a pipe to such exotic phenomena as supersonic flow and shock waves. The

study of fluid mechanics is based on thermodynamic principles and Newton’s

second law of motion. Fluid mechanics is the basis for such diverse fields as

acoustics, aerodynamics, biofluids, combustion, fire protection, magnetohydro-

dynamics, meteorology, and oceanography. Since the field of fluid mechanics is

vast, it is traditionally divided into several categories to facilitate the study of its

related topics. Here we briefly discuss the various categories involved in the study

of fluid mechanics. The unfamiliar terms used in this discussion are defined and

dealt with as we pace through the chapter.

One way to categorize the field of fluid mechanics is to consider the number of

phases involved in the flow. Single-phase flow considers only the flow of one

fluid such as water, air, steam, etc. On the other hand if water and steam for ex-

ample coexist in the flow, we then need to use the two-phase flow principles to

study such a condition. Single-phase flow is discussed in Chapter IIIa through IIIc

and two-phase flow in Chapter Va.

Another way to categorize the study of fluid mechanics is to consider whether

the flow of fluid is confined to a conduit or whether the fluid is flowing over an

object placed in the flow field. If the flow is confined to a conduit we are dealing

with internal flow. In such cases, we may be interested in determining the pump-

ing power required to establish certain flow rate. If the conduit is a piping net-

work, flow distribution in the network is of interest. On the other hand, if fluid

flows over an object, the condition is known as external flow such as the flow of

air over an airplane or the motion of a boat in water. External flow covers such

topics as lift and drag as well as flow of fluids in open channels. Chapter III is

mostly concerned with the internal flow of fluids. Some aspects of external flow

are discussed in Chapter IV.

Further categorization may be based on such physical properties of the fluid as

density and viscosity. As discussed later in this chapter with regard to density,

fluid may be considered incompressible like flow of liquids in a pipe or a fluid

may be compressible like flow of a gas in compressor. With regard to viscosity,

we consider two cases of real and ideal fluids also referred to as viscous and invis-

cid, respectively. Viscous effects are associated with friction. The advantages in-

herent in the ideal flow assumption enable us to obtain analytical solutions in

closed form to describe the flow behavior in certain conditions. Unlike ideal flu-

Sir Issac Newton (1643–1727) also contributed to calculus, optics, astronomy, fluid me-

chanics, and heat transfer

224 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

ids, which are incompressible and inviscid, dealing with real fluids involves pipe

roughness and such topics as unrecoverable frictional pressure drop. Chapter III

deals primarily with the flow of real fluids.

All of the above categories may be analyzed under steady state or transient

conditions. At steady state, there is no change in flow properties such as pressure,

velocity, and density with time. Transient analysis on the other hand is required

when there is a change in flow conditions. Examples of flow transients include

throttling a valve on a pipe carrying flow, turning off a running pump, or draining

a vessel. Chapter IIIb deals with both steady state and transient analysis of vis-

cous incompressible internal flows.

There are still other categorizations such as hydrostatics versus hydrodynamics

and the type of flow regime, (i.e. laminar versus turbulent). In this book, fluid

mechanics is divided into four chapters. In Chapter IIIa, we first discuss the fun-

damentals that are applicable throughout fluid mechanics. This includes deriva-

tion of the conservation equations for single-phase flow. The conservation equa-

tions for linear momentum and energy are used in conjunction with multiple

simplifying assumptions to derive the Bernoulli equation. This is followed by the

discussion on the concept of “head loss”. Chapter IIIb deals with incompressible

viscous flow through pipes, fittings, and in piping networks. Chapter IIIb is then

concluded with the study of unsteady flow of incompressible fluids. This includes

the discussion of such topics as tracking liquid level in surge tanks, time to drain

vessels, time to fill drained pipelines, and learning the fundamentals of such fast

transients as “waterhammer”. Flow of compressible viscous fluids including criti-

cal flow through pipe breaks is discussed in Chapter IIIc and the fundamentals of

two-phase flow in Chapter Va.

III

. Single-Phase Flow Fundamentals

1. Definition of Fluid Mechanics Terms

Stress is the result of applied force per unit area. The applied force acting on a

surface consists of two components one normal to the surface and the other paral-

lel or tangent to the surface. The component normal to the surface if divided by

the surface area is referred to as normal stress (

). A shear stress (

) is developed

due to the action of the tangential component on a surface.

Fluid is a substance that, under an applied shear stress deforms continuously.

A deformation always exists regardless of how small the applied stress might be.

There is no shear stress only when fluid is at rest. Depending on the magnitude of

the acting shear force, solids would initially deform. However, unlike fluids, such

deformation is not continuous. Any substance that is not fluid may be considered

solid. Fluids we are familiar with include liquids and gases. There are a few sub-

stances, such as toothpaste categorized as fluid even though they are neither a

fluid nor a solid. These are known as Bingham Plastic.

1. Definition of Fluid Mechanics Terms 225

Continuum hypothesis is the fundamental principle in thermofluids. In most

cases, it is impractical to study fluid behavior on a molecular basis. Therefore, we

use a macroscopic approach, defining a differential volume to represent a point in

the fluid. By using the average values for each point, fluid properties then vary

continuously throughout the fluid. Thus by ignoring the behavior of individual

molecules of the fluid and assuming that the fluid consists of continuous matter

we can define unique values for the flow variables; P, T, V,

, etc. For example,

we define density at a point for fluid as a continuum according to:

)V/(lim

'VV

δδρ

δδ

→

= IIIa.1.1

where

is a differential volume yet contains sufficient number of molecules to

make statistical averages meaningful. For all liquids and for gases at atmospheric

pressure, the limiting volume is about 10

–9

. Having defined flow field vari-

ables at a point, we use partial derivatives to determine the change in such vari-

ables between two points separated by elements of length. For example, if pres-

sure at point x, y, z is P, pressure at a point located dx, dy, and dz apart is P + dP

where dP = (∂P/∂x)dx + (∂P/∂y)dy + (∂P/∂z)dz.

Field refers to the flow variables (or parameters), such as pressure, velocity,

temperature, or density, as a function of position in a given region, which may

also be a function of time. For density for example, this is shown as

),,,( zyxt

ρρ

= .

Coordinate systems are used to represent the properties of a flow field in space

at any point in time. A fluid element in the flow field is determined by its position

vector. The position vector in Cartesian coordinates for example is expressed as

krjrirr

zyx

++= where i

, j

, and k

are the unit vectors. Similarly, the ve-

locity vector in Cartesian coordinates is comprised of three components; V

, V

and V

. In the literature, these are often represented with u, v, and w. The compo-

nents of flow velocity in cylindrical and spherical coordinates are represented by

, V

and V

, V

, respectively.

(x, y, z)

(x + dx, y, z)

(x + dx, y+dy, z)

(x, y+dy, z + dz)

(x, y, z)

(x , y, z + dz)

(x + dx, y + dy, z + dz)

(x , y+dy, z)

Figure IIIa.1.1. Position vector, velocity vector, and a differential volume in Cartesian co-

ordinates

A statistical approach is used for special cases to which the continuum assumption does

not apply. An example of such cases includes the passage of a rocket through the outer

layer of the atmosphere.

226 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

Body and surface forces are encountered in fluid statics and fluid dynamics.

Body forces consist of all forces that are developed in the fluid without physical

contact. Body forces are distributed over the volume of the fluid. Electromag-

netic and gravitational forces are examples of body forces arising in a fluid. Sur-

face forces such as shear and normal stresses on the other hand act on the bounda-

ries of a fluid through direct contact. A body force therefore is proportional to the

volume or mass, whereas surface forces, such as pressure and shear stress, are

proportional to the area. An element of a fluid in the Cartesian coordinate system

consists of six boundaries. Each boundary experiences two shear stresses tangent

to the boundary and a normal stress perpendicular to the boundary. These are

shown with two-letter subscript. The first index in the subscript refers to the axis

to which the boundary is perpendicular and the second index in the subscript re-

fers to the axis to which the stress component is in parallel. Hence,

refers to

the shear stress in the boundary the plane of which is perpendicular to the y-axis

and the direction of the stress, which is parallel to the z-axis. The nine component

stress tensor, also referred to as the stress matrix, is also shown in Figure IIIa.1.2.

Note, that

= – P +

, and

= – P +

where

implies normal

to the plane of its associated index.

Figure IIIa.1.2. Normal and shear stress components of an elemental control volume

Fluid kinematics and fluid dynamics both describe a flow field. The motion

of a fluid in a flow field is the basis of fluid kinematics. The effects of forces on

fluid motion are studied in fluid dynamics.

Kinematic properties refer to such quantities as linear velocity, angular veloc-

ity, vorticity, strain rate, and acceleration. Note that these are properties of the

flow field rather than the fluid. Thermodynamics and transport properties as well

as extensive and intensive properties were discussed in Chapter II.

Shearing strain is described below by comparing the response of a piece of

solid to an applied shearing force with the response of a liquid to the same applied

force. Shown in the left side of Figure IIIa.1.3 is a solid such as steel, firmly at-

tached to two plates. The lower plate is fixed while the upper plate is allowed to

move. If we now apply force F to the upper plate, in the case of steel we cause

point B to move a small distance to point B’. The application of force F also

causes shear stresses to be created at the interface between the steel and the upper

1. Definition of Fluid Mechanics Terms 227

plate to resist the applied force. The free-body diagram of the moving plate shows

(the center figure) that at equilibrium, F =

A. The angle

δα

is referred to as the

shearing strain (

= lim(į

/įt) as įt approaches zero). If we now apply the same

force to the plate in the right side of the Figure IIIa.1.3, it moves continuously.

In solids, the shear stress (

) is related to the shearing strain,

= f (

). For vis-

cous fluids,

δα

is a function of time as the upper plate is moving continuously due

to the applied force. In fluids, we therefore relate the shear stress to the rate of

change of the shearing strain (



) also known as shear rate, )(

γτ



f= . From the

linear velocity profile we can easily show that the rate of strain is equal to the

slope of velocity



= dV

/dy.

Moving Plate

Fixed Plate

Steel

δα

Water

= V(y) = V

y/H

= 0

= V

Figure IIIa.1.3. Shear stress as a function of velocity gradient

On the other hand, we also know that the rate of shearing strain is proportional

to the shear stress (



∝

), which in turn is proportional to the applied force F,

(

A = F). Thus



increases as

increases. Therefore, the shear stress is propor-

tional to the slope of the velocity profile

dydV

/∝

. For this relation to be

equal, we need a proportionality factor as discussed next.

Dynamic viscosity is the proportionality factor for shear stress and the velocity

profile. The dynamic viscosity, also referred to as molecular viscosity or simply

viscosity, is the most important property of a fluid. It is a measure of the response

of a fluid to an applied shear force. Mathematically we can write:

dydVT

)(

µτ

= IIIa.1.2

where

is viscosity and V

is the component of velocity along the x-axis. In this

case, shear stress acts on a plane normal to the y-axis. This mathematical relation

is a statement of Newton’s law of viscosity, showing that the velocity gradient is

the driving force for momentum transfer. Viscosity, similar to density, is a func-

tion of temperature. Change of viscosity versus temperature depends on the type

of fluid. For gases, viscosity increases with temperature. For liquids, viscosity

decreases as temperature increases.

Units of viscosity can be obtained from the definition of viscosity. Using shear

stress as force per area and velocity gradient as the inverse of time, units of viscos-

ity can be found as FT/L

. In British units, viscosity is expressed as lbf⋅s/ft

228 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

However, in most cases, viscosity is multiplied by g

to obtain units of lbm/ft·s. In

SI units, viscosity is generally given in centi-poise where 1 poise = 1 g/s·cm or in

units of Pa·s. Note: 1 centi-poise = 2.419 lbm/ft·hr.

Kinematic viscosity is defined as the ratio of dynamic viscosity to density,

ρµν

/= . Kinematic viscosity has units of ft

/h or m

/s. Note: in SI units, 1 Sto-

ke = 1 cm

/s. Hence, 1 ft

/s = 92,903 cs (centistokes).

Viscous and inviscid fluids are identified in the context of friction. A viscous

fluid causes friction when it flows. If the friction is negligible, then the fluid is in-

viscid and the flow is considered to be ideal.

Ideal gas versus ideal fluid. To avoid any confusion, recall that we used the

term “ideal gas” in Chapter IIa for any gas that conforms to the ideal gas rules. In

this chapter, we use the “ideal fluid” term for any fluid which is incompressible

and inviscid. Therefore while ideal gases at certain conditions may also behave as

an ideal fluid, ideal gases are generally not ideal fluids. Conversely, many liquids

under certain conditions may behave as an ideal fluid but they are clearly not ideal

gases.

Newtonian fluid is a type of fluid where the rate of deformation due to the act

of a shear stress is linearly proportional to the magnitude of the acting shear stress.

Therefore, all fluids that obey the above relation for shear stress are Newtonian

fluids. For example, water, benzene, alcohol and air are Newtonian fluids.

Strictly speaking, for a fluid to be Newtonian, four criteria should be met. These

criteria are discussed following the definition of the non-Newtonian fluids.

Non-Newtonian fluid is a fluid that does not conform to Newton’s law of vis-

cosity, in that viscosity for these fluids is a function of shear rate,

(



)dV

/dy. Non-Newtonian fluids include pseudo plastic, Bingham plastic, and

Dilatants. Pseudo plastic materials include polymer solutions, most slurries, mud,

and motor oil. Bingham plastic may indeed be considered Newtonian as they tol-

erate shear stress until the magnitude of the shear stress is equal to the yield stress

of the fluid. Then the fluid flows. Examples of Bingham plastic include tooth-

paste, jellies, some slurries, bread dough, blood, and mayonnaise. Dilatant fluids

are rare. The viscosity of such fluids increases with the increasing rate of defor-

mation. The suspensions of starch and sand serve as an example of dilatant fluids,

also referred to as shear thickening fluids. Finally, some non-Newtonian fluids

demonstrate a transient period before reaching the intended velocity. These are

known as viscoelastic materials, such as molten low-density polyethylene. Vis-

coelastics return only partially to their original configuration after being subjected

to shear stress.

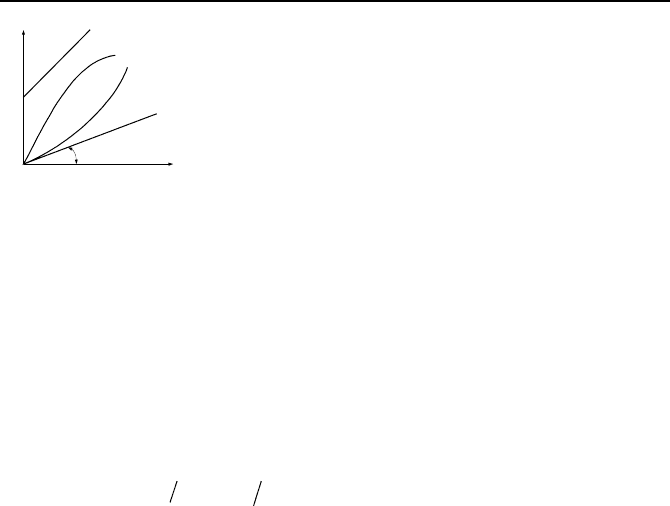
1. Definition of Fluid Mechanics Terms 229

/dy

Figure IIIa.1.4. Shear stress versus the deformation rate for Newtonian and non-New-

tonian fluids

Newtonian fluid criteria. Newtonian fluids meet four criteria. a) As dis-

cussed earlier, the stress is linearly dependent on the velocity gradient. b)

Stresses due to an applied force are symmetric. Before discussing the other crite-

ria let’s elaborate. We derived a relation between flow velocity in the x-direction

and the shear stress in a plane normal to the y-axis and parallel to the x-axis. The

first criterion requires that

/dy =

. We also note that if the fluid flows

in the direction of the y-axis, we can similarly write

/dx =

. In gen-

eral, a fluid can flow in any arbitrary direction in the xy-plane. Hence, in general

we should write:

= )( dxdVdydV

We can also write similar relations for flow in the xz- and yz- planes. In tensor no-

tation;

(

)

ijjijiij

dxdVdxdV // +==

µττ

IIIa.1.3

c) Shear stress is related to the instantaneous value of the derivative of velocity.

This criterion rules out the effect of some non-Newtonian fluids such as viscoelas-

tic materials. d) For stationary fluids stress is isotropic. This is to exclude such

other non-Newtonian fluids as Bingham plastic. Figure IIIa.1.4 shows the behav-

ior of shear stress for various materials.

No-slip condition for Newtonian and non-Newtonian viscous fluids is an im-

portant concept in that a fluid does not have any motion relative to the solid

boundary in contact with the fluid. Hence if the solid boundary is at rest, fluid ve-

locity is zero. Likewise, if the solid boundary is a plate in motion, the fluid parti-

cle at the surface also moves at the same speed as the plate. Thus, as a boundary

condition (V

fluid

)

surface

= V

surface

Surface tension is a liquid property. There are inter-molecular forces in the in-

terior of a liquid, which result in no net force applied to a molecule as the mole-

cules are equally attracted to each other. However, for the molecules on the liquid

surface, while the inter-molecular forces act towards the interior of the liquid,

there are no forces to counter act. Hence, there is a net unbalanced cohesive force

towards the interior of the liquid. Considering a semi-hemispheric drop of a liquid

of radius R, we can represent the net unbalanced force as

∆P acting on the cross

sectional area,

. Where ∆P = P

interior

– P

exterior

. This force gives rise to surface

230 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

tension (

) acting on the perimeter, 2

R. Thus, the surface tension becomes

∆P(

)/2

R = ∆PR/2.

Bulk modulus is an indication of the fluid compressibility (i.e., density varia-

tion within a flow) and is defined as E

= dP/(d

). High values of bulk modulus

indicate the fluid is nearly incompressible. Liquids have generally high bulk

modulus hence, liquids, for most practical purposes, can be considered incom-

pressible. Per above definition, the bulk modulus has the same dimensions as

pressure. In British Units it can generally be written as psi and in SI units as Pa.

Speed of sound is a measure of propagation of disturbances in a fluid. The

speed of sound is related to the fluid properties in which the disturbance is propa-

gating. This relationship is expressed as

ddPc /= . It can be shown that for

ideal gases undergoing an isentropic process, the speed of sound is given as

cRT

= where T is the absolute temperature of the fluid and

= c

. The

ratio of the speed of an object to the speed of sound in the same medium as that of

the object is called the Mach number (Ma). If Ma is less than, equal, or greater

than 1.0, the object is moving at a subsonic, sonic, or supersonic speed,

respectively.

Streamlines are useful in relating the fluid flow velocity components to the ge-

ometry of the flow field. A streamline is defined as the line drawn tangent to the

velocity vector at each point in a flow field. By definition, there is no flow across

a streamline.

Steady and unsteady flows depend on the frame of reference. In the Eulerian

approach, as described in Section 2, if flow at every point in the fluid is independ-

ent of time, then the flow is steady, otherwise it is unsteady (Figure IIIa.1.5).

Laminar and turbulent flows are applicable only to viscous fluid flow and are

identified based on the streamlines. The laminar or purely viscous flow moves

along laminas or layers. In laminar flow, there is no microscopic mixing of adja-

cent fluid layers. Turbulent flow has velocity components with random turbulent

fluctuations superimposed on their mean values. The Reynolds number, after Os-

borne Reynolds (1842-1912), is a dimensionless variable whose value determines

whether flow is laminar or turbulent. The Reynolds number is defined as Re =

V∆/

where in this relation ∆ is an element of length. For flow over a flat plate

for example,

∆ = L and for flow inside pipes, ∆ = D where D is the pipe diameter.

For external flow over flat plates, flow remains laminar as long as Re < 5E5 and

for internal flow inside conduits flow remains laminar as long as Re

≤ 2000.

Turbulent flow viscosity is of two types; molecular,

as defined earlier, and

eddy as defined in Chapter IIIb. The molecular viscosity of Newtonian fluids is

independent of location, boundaries, and the flow regime (i.e., laminar or turbu-

lent). The eddy viscosity on the other hand depends on all of these factors.

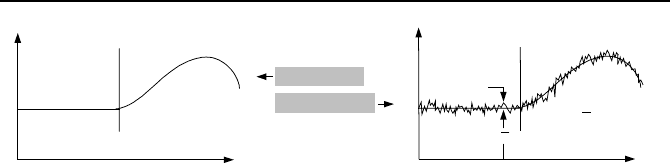
1. Definition of Fluid Mechanics Terms 231

Steady Flow

Unsteady Flow

Steady Flow

Unsteady Flow

V = V + V'

Laminar Flow

Turbulent Flow

Figure IIIa.1.5. Variation of axial velocity with time for laminar and turbulent flows

Compressibility and incompressibility are flow properties in addition to be-

ing fluid properties and are based on the variation in fluid density. In an incom-

pressible flow, the variation of density within the flow field is negligible. Gener-

ally, liquids may be considered incompressible, whereby density is a function of

temperature and a weak function of pressure (hence, according to Equation IIa.6.7,

∆h ≈ v∆P). For water, the bulk modulus is about 3E5 psi (2 GPa) and as predicted

by dP = E

, it requires very high change in pressure to obtain a slight change

in density. Therefore, in most cases flow of water may be considered incom-

pressible. However, there are special cases (such as waterhammer, discussed in

Chapter IIIc) that the compressibility of the liquid must be accounted for and the

flow must be analyzed as compressible.

Compressibility in gases is more subtle. While gases are easily compressed

(such as gas pressurization in compressors), in many applications gases may be

treated as incompressible flow. Generally speaking, the compressibility effects for

gases may be neglected as long as the flow velocity remains below 30% of the

sonic velocity in the fluid. If a fluid is compressible, an abrupt change in pressure

is not felt instantaneously throughout the flow field. In contrast, for incompressi-

ble fluids, such pressure disturbances are propagated at very high sonic wave ve-

locity.

Boundary layer is a thin layer of fluid, developed whenever a flowing viscous

fluid comes in contact with a solid. Velocity within this layer drops from the bulk

fluid velocity, (V

)

to zero at the surface of the solid. Laminar and turbulent

boundary layers are compared in Figure IIIa.1.6. This figure also shows the com-

parison between the flow over a flat plate and inside a pipe. In both cases, flow

velocity at the surface of the solid is zero and at the edge of the boundary reaches

practically the velocity of the bulk stream. Hence, inside the boundary layer, vis-

cous effects are present as the shear stress retards the flow. In the free stream, the

viscous flow behaves as if it is inviscid. In the case of the flow inside a pipe, the

region from the entrance to the pipe where the boundary layer is developing is

known as the entrance length or entrance region. Subsequently, the boundary

layer is established where flow is fully developed and a unique velocity profile ex-

ists. For flow over flat plates, transition from laminar to turbulent flow most

likely occurs at Re

≅ 5E5. For flow inside tubes, transition begins at Re = 2000

and flow becomes fully turbulent at Re

≥ 4000.