Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

292 IIIb. Fluid Mechanics: Incompressible Viscous Flow

∂

−=

)(

max

Therefore, the velocity profile in terms of maximum velocity at any axial location

can be written as:

max

)(

−=

IIIb.2.2

The volumetric flow rate can be obtained by using its definition:

drVrAdV

∆

∂

−==⋅=

³³

128128

)2(V



IIIb.2.3

where the differential pressure

∆P over length L due to friction is defined as ∆P =

– P

Wall Shear Stress In Terms of Average Velocity

To obtain a relationship between shear stress at the wall and flow average veloc-

ity, we first note that:

rxw

∂

−===

)(

ττ

All we need to do is to relate the pressure gradient to the average flow velocity.

This can be accomplished by using the results obtained in Example IIIb.2.1 by

substitituting for c

from Equation IIIb.2.1 to obtain:

∂

−=

Later in various chapters, the average flow velocity is also shown by V. Solving

for pressure gradient, we find:

µµ

−=−=

∂

To write P/ x in terms of K.E., we divide and multiply by 2/V :

−=−=

∂

164

µµ

IIIb.2.4

The first bracket can be written as (64/Re) and shown as f = 64/Re, where f is

known as friction factor or the Darcy-Weisbach resistance coefficient. We discuss

2. Steady Internal Incompressible Viscous Flow 293

the friction factor in more details later in this chapter. Substituting the result ob-

tained for

∂P/∂x in the relation for

, the wall shear becomes:

∂

−=

242

IIIb.2.5

Fully Developed Turbulent Flow Inside Pipes

Similar to the laminar flow, once past the entrance region, the steady turbulent

viscous flow inside pipes becomes fully developed. In most engineering applica-

tions, flow is generally turbulent and the profile for shear stress distribution re-

mains the same as derived in the previous section. However, unlike laminar flow,

we can not use the Newton law of viscosity to derive the velocity distribution from

shear stress.

As discussed in Section 1, in turbulent flow, shear stress is enhanced by addi-

tion of the Reynolds shear stress to the Newton law of viscosity:

−=

where y is the distance from the pipe wall. To determine a velocity profile for tur-

bulent flow, we would have to use the experimental data obtained for a smooth

pipe, as shown in Figure IIIb.2.3.

To simplify the task of model making using the experimental data, Hinze iden-

tifies two major regions in the velocity profile. The first region is located close to

the wall. In this region, viscous forces are dominant and the flow is laminar. This

region is referred to as the viscous wall layer or viscous sub-layer. The second re-

gion includes the bulk of the flow and is referred to as the turbulent core. In this

region, turbulent shear is dominant. The overlap or the buffer layer is located be-

tween the above regions. In the buffer layer both turbulent shear and viscous

shear exist. Prandtl, von Karman, and Millikan used the experimental data to for-

mulate the velocity profile in the viscous sub-layer, the turbulent core, and the

buffer layer, respectively. These profiles are expressed in terms of dimensionless

velocity versus dimensionless distance from the wall. To obtain non-dimensional

values, a factor called the friction velocity,

V , is used:

ρτ

V =

Note that

V is not actually a flow velocity, rather it is a term that has dimensions

of length per unit time. Defining

xxx

VVV =

and

yVy =

where

ρµν

/= is the kinematic viscosity, we get a plot of

V versus y

as shown in

the semi-log scale of Figure IIIb.2.3. The velocity profiles that best fit data for

each region are given as:

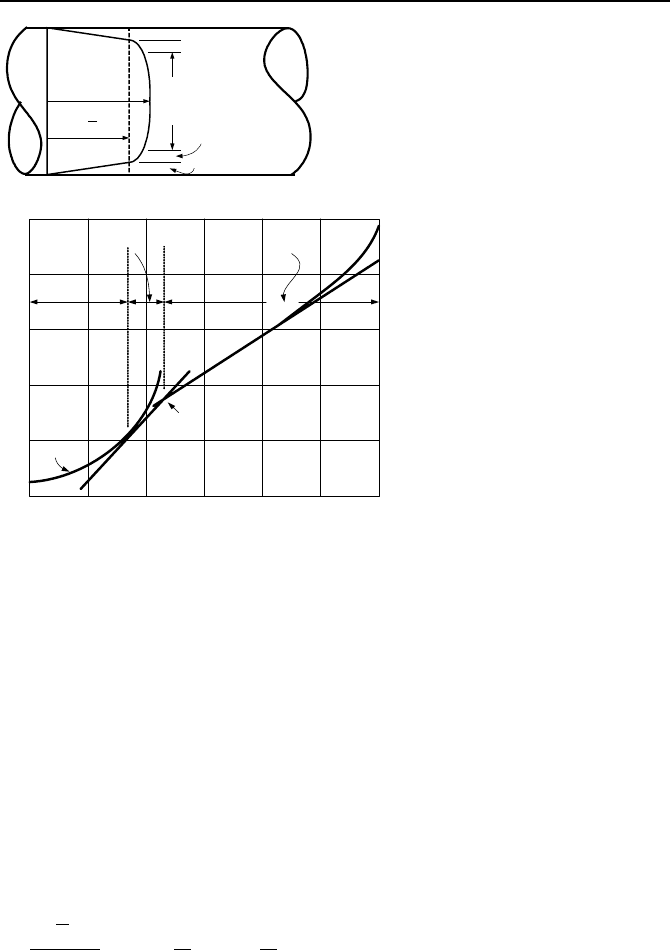
294 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Turbulent

Core

Buffer Layer

Viscous Sublayer

max

Molecular

Eddy Viscosity

Molecular &

Eddy Viscosity

Laminar

Sublayer

Constant

Shear

= y

= 2.5 ln y

+ 5.0

= 5.0 ln y

-3.05

Turbulent

Core

30 1000100105

Figure IIIb.2.3. Universal turbulent velocity distribution

= yV

3)ln(5 −=

305 ≤≤

5)ln(5.2 +=

30>

While these profiles are representative of flow inside pipes they have two disad-

vantages for practical applications. First, a three-region model would need to be

used to represent the flow. Second, there is a discontinuity between the formula

for one region and the formula for another region. This results in a system of

equations with discontinuities in the derivatives. Therefore, it is preferable to find

a single velocity profile that reasonably describes turbulent flow in pipes. Pai rec-

ommended a profile in the form of a power series:

)()(1

)(

max

++=

for both laminar and turbulent flows. Brodkey extended this solution to non-

Newtonian fluids. An even simpler profile originally suggested by Nikuradze for

the turbulent core region is:

3. Pressure Drop in Steady Internal Incompressible Viscous Flow 295

/1/1

max

)(

−=

= IIIb.2.6

where R is pipe radius. Hinze showed that the exponent n is a function of the Rey-

nolds number, ranging from 6 to 10. In most applications, a value of 7 is used for

the exponent n. Hence, the profile for fully developed turbulent flow is referred to

as a one-seventh power profile. Although the one-seventh power profile is very

easy to use, it has its own drawbacks. For example, a simple profile is not appli-

cable close to the wall nor does it give zero slope at the pipe centerline.

Now that velocity profiles of laminar and turbulent flows were discussed, we

return to Equation IIIb.2.3 to derive a very important relation in fluid mechanics

applications namely, the calculation of pressure drop in pipes for the flow of vis-

cous fluids.

3. Pressure Drop in Steady Internal Incompressible Viscous Flow

Here we are primarily concerned with one-dimensional flow. As discussed in

Section IIIa.3.3, the unrecoverable pressure drop is intrinsically associated with

the flow of viscous fluids. For comparison, recall from the Bernoulli equation that

any change in pressure in the flow of an ideal fluid occurs only due to a change in

flow area or elevation. This is referred to as recoverable pressure drop. Con-

versely, the flow of viscous fluids is associated with pressure drop even if both the

flow area and the flow path elevation remain the same. This is referred to as unre-

coverable pressure drop. Therefore, the goal here is to calculate the unrecoverable

pressure drop for both fully developed laminar and turbulent flows in pipes. Ex-

pectedly, we should be able to derive an analytic relation for pressure drop in

laminar flow whereas the turbulent flow pressure drop would have to be obtained

from experimental data.

Pressure drop is either due to the surface condition of the conduit wall carrying

the fluid or due to the presence of fittings and valves. We begin with the study of

pressure drop in straight pipes.

Pressure Drop in Fully Developed Laminar Flow

Pressure drop in steady, incompressible, fully developed laminar flow inside pipes

was obtained from the solution to the conservation equation for momentum in

Section 1. The pertinent relation to this discussion is Equation IIIb.2.3, which

may be rearranged to obtain a relation for pressure drop:

DVL

PPP

πµ

)4/(128

==−=∆

which states that pressure drop in a pipe depends on three factors, type of fluid

(appears as viscosity), pipe dimensions (appears as the ratio of pipe length over

pipe diameter), and average flow velocity. As discussed in Chapter IIIa, to com-

296 IIIb. Fluid Mechanics: Incompressible Viscous Flow

ply with tradition in hydraulics, the pressure drop may be expressed in terms of

height of fluid or head. This loss in fluid head between two points is due to fluid

viscosity. Hence, the pressure drop associated with friction head, h

, is given as:

gPP h

=− IIIb.3.1

Substituting for pressure drop, the frictional head loss becomes:

)(64

where two times the average flow velocity is multiplied in both numerator and de-

nominator. The terms are then grouped in separate ratios. There are two advan-

tages for the multiplication by twice the average flow velocity. First, if density is

positioned in the denominator of dynamic viscosity, this ratio constitutes the di-

mensionless Reynolds number, accounting for the inertial to viscous effects. The

second advantage is that the square of velocity divided by 2 provides the specific

kinetic energy associated with the flow of fluid. The net results can be summa-

rized as:

2Re

64)(h

Laminar

IIIb.3.2

This relation applies to laminar flow i.e. as long as the Reynolds number stays be-

low 2200. Recall that the ratio of (64/Re) is referred to as the friction factor (i.e.

Laminar

= 64/Re) and the Reynolds number is the ratio of inertial to viscous forces:

DmVD

νπµµµ





==== IIIb.3.3

Pressure Drop in Fully Developed Turbulent Flow

An analogy with laminar flow head loss can be used to derive a formula for turbu-

lent flow to get:

TurbulentTurbulentf

)h(

= IIIb.3.4

Expectedly, the friction factor in turbulent flow depends not only on fluid viscos-

ity but also on the pipe wall roughness. Colebrook used the experimental data ob-

tained by Prandtl’s student Nikuradze to develop a correlation for friction factor as

an implicit function of pipe roughness and Reynolds number. Subsequently,

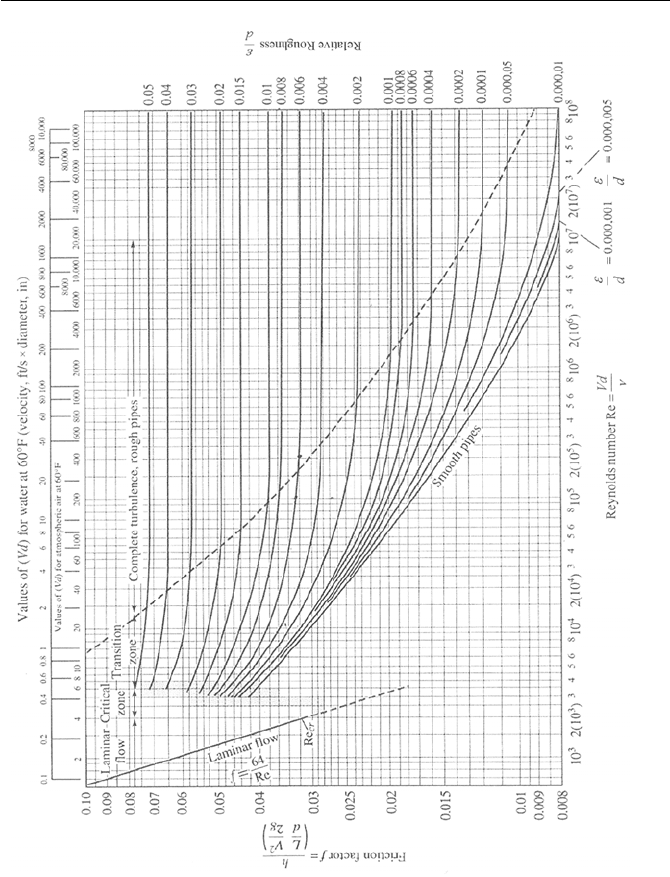
Moody plotted the correlation in a semi-log chart, which has become the well-

known Moody diagram, as shown in Figure IIIb.3.1 (Moody 44). The Colebrook

correlation is given as:

+−=

ColebrookColebrook

51.2

7.3

log0.2

IIIb.3.5

3. Pressure Drop in Steady Internal Incompressible Viscous Flow 297

In this correlation, D is the pipe inside diameter and

is the roughness of the pipe

wall. Typical values for pipe roughness for some commercial pipes are shown in

Table IIIb.3.1. Equation IIIb.3.5 is implicit in f. Hence, it requires iteration to

solve for the friction factor. An example for such iteration is provided in Chapter

VII. Haaland suggested an explicit formulation for friction factor as a function of

pipe roughness and Reynolds number:

+−≈

11.1

2/1

Haaland

7.3

9.6

log8.1

1 D

IIIb.3.5-1

As shown in Table IIIb.3.1, the pipe roughness (

) is on the order of 0.00085 ft

for cast iron pipes, 0.0005 ft for galvanized iron, and 0.00015 ft for commercial

steel. Churchill suggests the following explicit formula:

29.0

Churchill

)]Re/74.57.3/[ln(

325.1

IIIb.3.5-2

The friction factor calculated from Churchill’s formula is within 1% of that calcu-

lated from the Colebrook correlation and at the same time prevents iteration.

Moody has recommended a similar friction factor:

+×+=

333.0

10210055.0

Moody

IIIb.3.5-3

Table IIIb.3.1. Typical values of average roughness of commercial pipes

Material

(ft)

(mm)

C Hazen-Williams n Manning

Asbestos cement

Asphalt cast iron

Cast iron

Commercial steel

Concrete

Copper tube

Drawn tubing

Galvanized iron

Glass

PVC, plastic

Riveted steel

Welded Steel

Wood stave

Wrought iron

–

0.0004

0.00085

0.00015

0.001 – 0.01

smooth

0.000005

0.0005

smooth

0.003 – 0.3

0.00015

0.0006 – 0.003

0.00015

–

0.120

0.260

0.046

0.3 – 3.0

smooth

0.0015

0.15

smooth

0.9 – 9.0

0.046

0.18 – 0.9

0.046

140

–

130

–

120 – 140

150

–

150

110

120

–

120

0.011

0.013

–

0.011 – 0.014

0.010

–

0.016

0.010

0.009

0.013 – 0.017

0.012

–

0.012

298 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Figure IIIb.3.1.

Friction factor for fully developed flow in pipes and tubes

3. Pressure Drop in Steady Internal Incompressible Viscous Flow 299

In most engineering applications, especially in nuclear engineering, smooth pipes

are used. McAdams recommends the following friction factor for fully developed

turbulent flow in smooth pipes:

2.02.0

McAdams

)/(

184.0

(Re)

184.0

µρ

f ==

IIIb.3.6

For fully rough (wholly turbulent flow) and high Reynolds number, the frictional

effects are produced by roughness alone without the viscous action. For this re-

gion, Vennard derives the friction factor as:

[]

10Vennard

)/(log214.1

−

Having f, we can find pressure drop. To do this we note that the Reynolds number

is dimensionless, density in British Units is in lbm/ft

, velocity in ft/hr, diameter in

ft, and dynamic viscosity in lbm/ft·hr. Having the head loss associated with inter-

nal flow of fluids, pressure drop can be readily found by back substitution of

Equations IIIb.3.4 into Equation IIIb.3.1. Therefore, pressure drop corresponding

to the frictional head loss for a viscous fluid flowing between two points can be

calculated as:

fPPP

ρρ



=−=∆

IIIb.3.7

To have pressure drop in British units expressed as lbf/ft

, the pipe length and di-

ameter should be in ft, density in slug/ft

, and velocity in ft/s. Equation IIIb.3.7 is

known as the Darcy formula. This equation is used in pipe sizing, in a pump se-

lection analysis, and other engineering applications. It must be emphasized that

Equation IIIb.3.7 should be used to calculate pressure drop due to flow friction be-

tween two points located on a straight piece of pipe. Should there be an exception

to this limitation, additional pressure drops may need to be considered, as dis-

cussed later in this chapter.

Example IIIb.3.1. Fluid flows into a 3 in pipe with Re = 200,000. Compare the

friction factor if the pipe is smooth with the friction factor if the pipe is made of

cast iron.

Solution: First, for the smooth pipe, we can get reasonably accurate values by us-

ing correlation IIIb.3.7:

f = 0.184Re

-0.2

= 0.184(200,000)

-0.2

= 0.016

For the cast iron pipe, we get a reasonably accurate value from the Churchill cor-

relation without any need for iteration:

29.0

)]Re/74.57.3/[ln(

325.1

028.0

]}000,200/74.5)12/37.3/(00085.0{ln[

325.1

29.0

≈

+×

The corresponding pressure drop for the cast iron pipe is almost twice that of the

smooth pipe.

300 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Example IIIb.3.2. A pipeline, made of commercial steel, carries oil at a rate of

0.5 m

/s. The pipe length and diameter are 1 km and 300 mm, respectively. Find

pressure drop in this pipeline. Oil properties:

oil

= 850 kg/m

and v

oil

= 1.5E–5

/s.

Solution: We use the Churchill correlation to find f to be used in Equa-

tion IIIb.3.7. This in turn requires us to calculate the Reynolds number:

Re = VD/v = VDA/(vA) = V



D/vA

Pipe flow area is A =

/4 = 3.14(300/1000)2/4 = 0.0707 m

Hence, Re = 0.5(300/1000)/(1.5E-5 × 0.0707) = 141,443

29.0

)]Re/74.57.3/[ln(

325.1

0177.0

]}444,141/74.5)3007.3/(046.0{ln[

325.1

29.0

≈

+×

MPa25.1

)0707.0(8502

)5.0850(

)

3.0

1000

0177.0(

)(

××

==∆



Example IIIb.3.3. The riser of a containment spray system carries water at a rate

of 1250 GPM (78.86 lit/s) to the spray header located 190 ft from the pump center

line. The riser is an 8 in (20 cm) smooth pipe. Find the pump pressure rise to off-

set the pressure drop in the riser due to friction and elevation. Water is at 60 F.

Solution: We find the pressure drop due to friction and elevation by following the

steps outlined below:

D = 8/12 = 0.667 ft (20.32 cm)

A =

(0.667)

/4 = 0.349 ft

(0.0324 m

)



= 1250 (60/7.481) = 10,025 ft

/h = 2.785 ft

/s (78.86 lit/s)

(60 F) = 2.76 lbm/ft·h,

(60 F) = 62.35 lbm/ft

, v(60F) = 0.0443 ft

/h (1.143E-6

/s)

Re = V



D/vA = [10,025 × 0.667] / [0.0443 × 0.349] = 432,608

f = 0.184/Re

0.2

= 0.0137

= f(L/D)(



/2gA

) = 0.0137(190/0.667) ×(2.875

/2× 32.2×0.349

) = 4 ft

Equation IIIa.3.31 is applicable:

fsei

hh)()

(

)(

+−=−+−+−

We simplify this equation for the following reasons. First, the kinetic energy

terms cancel out since V

= V

. Next, we note that there is no pump between point

i and e hence, h

= 0. This is because the control volume includes the pipe run

from the discharge of the pump to the spray header. Also noting that Z

– Z

= H,

thus:

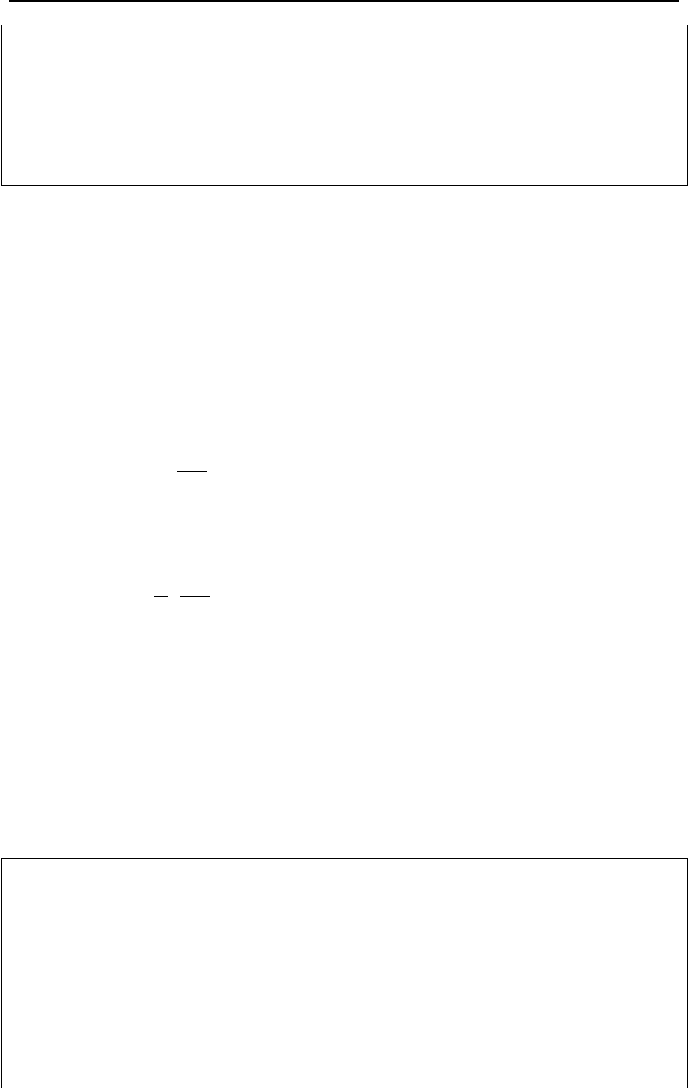
3. Pressure Drop in Steady Internal Incompressible Viscous Flow 301

gPP

fei

)hH( +=−

Substituting

– P

= 62.35(190 + 4) 32.2/32.2 = 84 psi (0.58 MPa)

In this problem, we did not consider frictional losses due to valves and fittings.

These are included in the so-called minor losses, which are discussed later in this

chapter.

Other Pipe Friction Models

The Darcy formula, also known as Darcy-Weisbach, is the most widely used

model for the calculation of pipe friction. An empirical equation known as Hazen-

Williams is often used in the calculation of frictional losses in piping networks for

water. Another empirical equation, known as Manning is an adaptation of open-

channel equation applied to the flow of water in rough pipes. The Darcy-

Weisbach formula is given in Equation IIIb.3.7. The Hazen-Williams formula is

given as:

54.0

63.0

55.0

CDV

IIIb.3.8

and the Manning formula as:

2/1

3/2

59.0

IIIb.3.9

where constants C and n are given in Table IIIb.3.1. Note that in the Hazen-

Williams and Manning formulae D is in ft and V in ft/s. Vennard shows that both

the Hazen-Williams and Manning models can be cast into the Darcy formula if f is

expressed as

)Re/(1090

15.085.1

−

and as

3/12

/185 Dnf

= , respec-

tively. The advantage of the Hazen-Williams and Manning formulae is that to

find the pipe diameter for a given head loss, no iteration is needed. This is dem-

onstrated in the following example.

Example IIIb.3.4. Two water reservoirs are located 5 miles apart and have an h

= 250 ft. Find the pipe diameter to carry a steady flow of 25 ft

/s. The pipe is

welded steel.

Solution: We first use the Hazen-Williams formula. From Table IIIb.3.1, C =

120 hence,

[25 / (

/4)] = 0.55 × 120 D

0.63

[250/(5 × 5280)]

0.54

Solving for D, we find, D

H-W

= 1.973 ft or 23.7 inches. We next use the Manning

formula: