Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов

Подождите немного. Документ загружается.

где

F(r) = fdr'/o(r')*(r'->r) +

+ jdr

V(rr)

Г —Гг

К(гг-+т)\

(5.4.13)

J((f4f) = l ехр(-т(г'->г))

4я |r—r'|

т(г'->г) = ^ ' 2(r-£0)dg.

Величина т (r' ->r) называется оптическим расстоянием от точки

Р'

(г') до точки Р (г).

До сих пор предполагалось, что внешние источники нейтронов изо-

тропны. Если предположить, что / = / (г, й) и V = V (г, Q), то снова

придем к интегральному уравнению (5.4.12), где функцию F (г) не-

обходимо заменить следующей:

\dtrvU

J^^||^^nU(r

^r). (5.4.14)

? \

r|/l l

Более подробные сведения о постановке задачи о диффузии нейтронов

в случае неизотропной индикатрисы рассеяния можно найти в книге

Б.

Дэвисона [81].

Интегральное уравнение (5.4.12) запишем для простейших геоме-

трий. Предположим, что среда, заполняющая область Z), однород-

на.

Рассмотрим сначала случай плоскопараллельной геометрии. Будем

считать, что на слой толщиной Н падает изотропный поток нейтронов

интенсивностью V+ при z = 0 и V" при z = Я. Внутри слоя источ-

ники распределены по закону /

(г). В таких предположениях, оче-

видно, решение задачи ф

будет только функцией z.

Полагая х =

у = х

\ z =

лг

;

dx' =

dx'dy'dz'\

dr? = dxdy\

г—г

= COS

0 =

z-z'

+{z

интегральное уравнение Пайерлса запишем в следующем виде:

q>o(z)~2

\<po(z')K(Z\z-z'\)dz' +

F(z),

(5.4.15)

где

F(z) = §dz'f

{z')K(Z\z-z'\) +

+ V+P(2

) + V-P(2{H-z));

K(2|z-

'|)=— f dx' f ^exp(-Sr)

4я J J r

00 —oo

;

г»

— 00 —00

(5.4.16)

Вычислим интегралы в правой части последних равенств в (5.4.16).

С этой целью положим х — х' = р cos а, у

—

у' = р sin а. Тогда

ка\

='[\-

p(-

P .

' '' 2 J

(г_г')2

riiz)-

ех

р(-

Ур

гг

)рф

2 J

(р2+г2)

з/2

(5.4.17)

Перейдем к новой переменной интегрирования t по формуле 1=2 X

X Т^Р

+ (z

—

z')\ В результате получим

Я(2|г-г'|) = у ?

-^^;

Р(2*)

= ^ JH£iz£> <*/.

S\z-z'\ Sz

(5.4.18)

exp (—t)

Учитывая, что J df = £

(л;), имеем

/С (21

г—г'

£*!

(21

г—г'

|)/2;

P(2z) = 2z£

(2z)/2. (5.4.19)

В заключение вычислим функцию F

(z)

в том предположении, что

источник единичной интенсивности сосредоточен в плоскости 2 = 0,

а потоки нейтронов из вакуума отсутствуют, т. е. V

= 0. Тогда

(г)

= (1/2) Е

(2z). В этом случае интегральное уравнение Пайерл-

са (5.4.15) примет вид

Фо

(z)

= ^jdz'Mz')E

^\z-z'\) + -^-E

(2z). (5.4.20)

Если среда бесконечна, то (5.4.20) переходит в следующее:

Фо

(2) =

Т"

Лгщ

} El (S

|} +

El(Ег)

21)

Следует отметить, что та часть решения, которая представлена функ-

цией В

(z) = (1/2) Е

(2z), описывает полное число нейтронов, ко-

торые не испытали ни одного соударения при движении от источника

до плоскости z = const. Эти ней-

троны называют нерассеянными.

Рассмотрим далее случай сфери-

ческой геометрии. Будем считать,

что область D представляет собой шар

радиусом R. На внешнюю границу

шара со стороны вакуума падает

изотропный поток нейтронов плот-

ностью VQ. Внутри шара заданы

источники нейтронов /

(г).

В указанных предположениях ре-

шение задачи ф

будет функцией

только г.

Учитывая соотношения (рис. 5.2)

Рис.

5.2. Система координат для

сферически-симметричной обла-

сти

г—rf

г|

= cos

R—г

cos

yfl2

2_2/?r'cosfl

имеем

Фо (г)

= S

(г') К

(г'

г)

dr' +

(г),

(5.4.22)

где

F(r)=]h{r')K(r'-+r)dr' +

VoP(r\,

ехр(~-2 Уг'2 + r*—2/т>)

-1

' 2 J/ r'*+r*-2rr'у.

—e. jd^R-r^

zVR2+r2

]

—

(5.4.23)

Здесь мы перешли к новой переменной интегрирования [г = cos ft

и произвели интегрирование по азимуту г|). С помощью замены пере-

менной интегрирования

\х

на t = 2]/7'

+ г

—

2гг'\л

второе и третье

соотношения системы (5.4.23) приведем к виду

2|г+г'|

"'-'>-77 1

ехр(—0

Л;

Я(Г):

4г

2|г-г' |

2(Я + г)

ех|)(-/)

2(7? + /')

Л-

4г2

2(Я-г)

Г ехр(—f)d/.

(5.4.24

2(Я-г)

С учетом соотношения (5.4.19) будем иметь

К(г'-»г) = (г'/г)1Е

(1 |r-r'|)-£i(2|r + r'

|)]/2;

(г)

= 2 (Я

-г

) [£

(2 (Я-г))-£

(S (/? + г))]/4г+

[ехр

(-2 (#-r))-exp (-2

+ г))]/4г2.

Полезно обратить внимание на следую-

щий факт. Если предположить, что поток

нейтронов, падающих на шар со стороны

вакуума, отсутствует, т. е. V

= 0, то с

помощью соотношений лр

(г)

ср

(г) и

rfo (

) = / (

) уравнение (5.4.22) пребра-

зуется к виду

(5.4.25)

Ф(Г) =

"Т |ф(0^(2|г-г'Нг' +

+ Y j/(r')£i(2|r-r'|)dr\

-R

Таким образом, в этом случае интег^

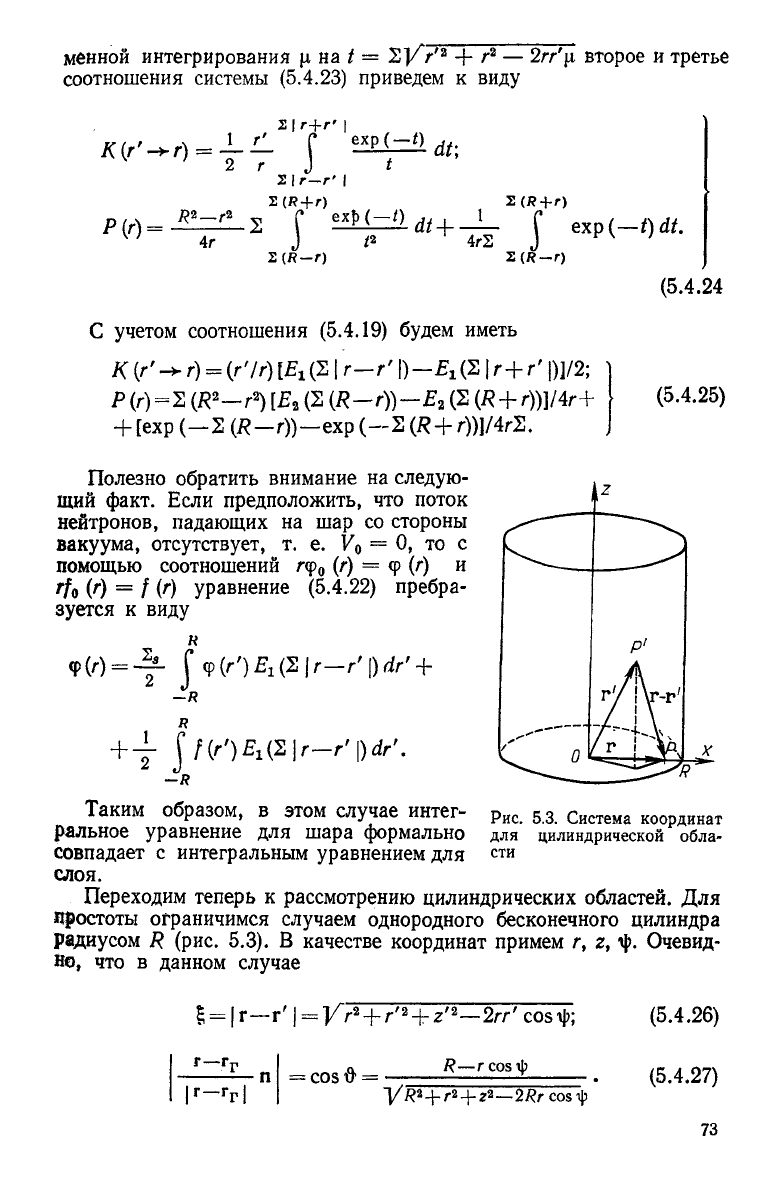
Рис> 5>3

. система координат

ральное уравнение для шара формально для цилиндрической обла-

совпадает с интегральным уравнением для

сти

слоя.

Переходим теперь к рассмотрению цилиндрических областей. Для

простоты ограничимся случаем однородного бесконечного цилиндра

радиусом R (рис. 5.3). В качестве координат примем г, г, ij). Очевид-

но,

что в данном случае

г—r'| = }/r

+ r'

+ z'

—2rr'cos\|>;

Г—r

г|

: cos

ft =

/?—rcosxp

У Я

—2Rr

cos \|з

(5.4.26)

(5.4.27)

Поскольку решение интегрального уравнения есть функция только

г, перейдем

интегральному уравнению (5.4.22),

где

- ехр(-~2 Уг2 + г

+ г

—2/т' cost|?)

+ г'

—2/т'

cosip

О —оо

F(r) = J f{r')K(r'-+r)dr +

VP(r)\

(5.4.28)

2я оо

О —оо

2я оо

Р(г)

= — f Л|> f

&(/?—rcos^)x

О —оо

exp(—Z y^2 4-r

—2/?rcos\|?)

(5.4.29)

Преобразуем ядро интегрального уравнения.

Для

этого представим

выражение

для К

{г'

->г) в

виде суммы двух членов:

> + r) = !-[[ dj[dz exp(~sVr

+ r-

+ e

^2rr-cos^)

2я U

+ г'

+ г

— 2/т' cosip

+ f <ty

Л exp(^Vr

+ r-

+ 2

+ 2rr-cos

)\ ^

J J r

+ r'

+ *

+ 2rr'cos\|) /

Примем далее

во

внимание следующие соотношения:

в(

*г)

Ы=0ЕЮ

Л;

Г Ко(хг)dx =

«Р

(-«?*+*)

dt.

(5.4.31)

С учетом выражений (5.4.31) получим

к (Г

г)=

ЙГ

Ко (ах)

/<о

(foc)

•

(5Л32)

где

a = |/>2-f

—

2rr'cos^; ^уУ +

г^Ч-2/T'COSI|>.

Выражение (5.4.32) преобразуем

виду

'-">=т„(|^J«.w<

p+f

[*.<Р>«

Р).

(МЛЧ

В первом слагаемом перейдем от переменной гр к а по формуле

cos

г|)

= (г

+ г'

— а

)/2/г', а во втором слагаемом осуществим за-

мену cosi|> = (б

— г

— г'

)/2/г'. Тогда окончательно приходим к вы-

ражению

* (г'-*г)=

7 * х

x$VoW<tt.

§ 5.5. НАХОЖДЕНИЕ ЭЛЕМЕНТАРНЫХ РЕШЕНИЙ ОДНОРОДНЫХ

ЗАДАЧ

Рассмотрим сначала однородное кинетическое уравнение в плоской

геометрии

n|e+2<p=^j<p(z

i')^'.

Пусть 2, 2

постоянны. Перейдя к безразмерной переменной

х = 2 г, запишем:

где с= 2

. Ниже получим семейство решений уравнения (5.5,1)

методом Фурье: решение ищем в виде

Ф = ехр (— x/v) O

(\i), (5.5.2)

где v — некоторый числовой параметр.

Решения такого вида назовем элементарными. Описанный способ

получения решений (5.5.2), которые можно интерпретировать как соб-

ственные функции уравнения (5.5.1), давно известен (см. по этому по-

воду библиографические ссылки в монографии Б. Девисона [81]).

Ван Кампен [340] заметил, что сингулярные собственные функции,

которые возникают в рассматриваемой задаче, могут быть интерпре-

тированы как обобщенные функции в смысле Соболева—Шварца [218,

57].

Эта концепция была перенесена К. Кейсом [266] на односкорост-

йую изотропную задачу. Он доказал полноту и ортогональность си-

стемы найденных собственных функций, нашел представления реше-

ний некоторых краевых задач через найденную систему функций. Ра-

бота [266] явилась основополагающей для большого числа работ, обоб-

щающих результаты Кейса на плоскую геометрию с неизотропным рас-

сеянием и зависимостью от скорости (см., например, работы Дж. Мит-

шса

[315],

Р. Желязны [83], Р. Беднажа и Я. Мика [257] и др.).

Подставляя (5.5.2) в (5.5.1), получаем уравнение для

(\i)

(l-|i/v)O

(|i) = -|- JOvOiVl*'- (5.5.3)

He уменьшая общности, можно потребовать, чтобы

$Ov(|i')V=l- (5.5.4)

—1

Учитывая это, из (5.5.3) получаем

Ov(|A) = cv/(2(v-|i))

(5.5.5)

или, интегрируя (5.5.5) по отрезку —

< \i < 1, имеем

|ф

у((

г)^=1 = -|-|^. (5.5.6)

Таким образом, получили уравнение для v:

= — In—

—. (5.5.7)

2 v—1

Известно

[266],

что существуют два корня уравнения (5.5.7): ± v

для всех с > 0. Известно также, что Im v

= 0, | Re v"

при

0<c<lHRev

= 0 при с > 1. Итак, мы нашли два решения урав-

нения (5.5.1) вида (5.5.2) с v = ± v

. Но этими решениями не исчер-

пывается все многообразие решений типа (5.5.2), ибо функция O

(|х)

может быть и обобщенной функцией. Уравнение (5.5.3) будет удовлет-

ворено, если решение

(ц) запишем в более общем виде:

Фу(р)~Р-^— + Mv)6(|i-v),

(

)

Z V — [А

где под Р/ понимается регуляризованное значение функции /, а б (*)

—

одномерная б-функция [57].

Число X (v) в формуле (5.5.8) определяется из равенства (5.5.4):

1 1

l =

\-^~

+Х{у)

(^-

)^.

(5-5.9)

-1 -1

Имеются две возможности нахождения элементарных решений урав-

нения (5.5.1).

Пусть v ( [— 1,1]; тогда второе слагаемое в (5.5.9) равно нулю

и имеются лишь два решения уравнения (5.5.1) с v = ± v

, которые

согласно (5.5.2) запишутся в виде

Фо±

(х,

\i)

= Ф

± (|i)

exp (=F

x/v

)

(5.5.10)

где

OO±(|I) = CVO/(2(V

=F|A)). (5.5.11)

Пусть v £ [— 1, 1]; тогда из (5.5.9) следует, что

1==

f^r+^

5Л2)

-1

Уравнение (5.5.12) послужит нам уравнением для выбора функции

(v). В этом случае элементарные обобщенные решения существуют

для всех v £ [— 1, 1] и выражаются формулой

<Pv

(х,

t*>)

= Фу (ц) ехр (— x/v), (5.5.13)

где обобщенная функция

(ц,) задается формулой (5.5.8), в которой

Mv)=l-2iln-}±2-. (5.5.14)

2 1—v

Таким образом, существуют два дискретных решения (5.5.10) и

континуум обобщенных решений (5.5.13). Справедлива

Теорема

5.5.1.

(\i<D

>{\L)G)

(\i)dii

при v=j£v\ (5.5.15)

-1

Для доказательства теоремы 5.5.1 будем рассуждать следующим

образом. Согласно равенству (5.5.3) для функций Ф

(ц), Фу' (ц)

должны быть выполнены уравнения:

(1 — |i/v) <D

(|i) =

с/2;

(1 — |*/v')

OV'

(|i) = с/2.

Умножая первое из них на O

> ([i), а второе

—

на Ф

((А),

вычитая

полученные уравнения друг из друга и интегрируя результат по

—

< \i <

находим

[(v

^-i_

-i] f©

,(,i)o

Gi),id,i=o.

Поскольку v' Ф v, из последнего равенства убеждаемся в справедли-

вости теоремы

5.5.1.

Используя формулы для Ф

, получаем следующие значения инте-

гралов:

j^l

^)d^N

0±

= ±^f^

~^j-, (5.5.16)

J|iO

'(|*)Ov(rtrf|A = iVve(v-v')

(5.5.17)

—i

где

= v [Я

(v) + JtW/4].

Теорема 5.5.2. Функции Ф

±(^) и Фу(^), v £ [— 1,

— яол-

ная

в L

[— 1,1]

система

функций.

Для доказательства теоремы требуется показать, что любую сум-

мируемую на [— 1, 1] функцию гр (|ы) можно записать в форме

г|)

М = а

Фо+

(|А)

+ во- Фо- (ц) + j A

(v)

([*)

d v. (5.5.18)

-l

Для этого конструктивно построим представление (5.5.18). Сначала

допустим, что представление (5.5.18) возможно. Из этого допущения

определим, чему должны быть равны коэффициенты #о±, A (v). Из

теоремы 5.5.1 и равенства (5.5.16) следует, что

o± = ^i ||*ФО±0А)Ш^. (5.5.19)

-1

Значит, достаточно рассмотреть функции г|/ (|и) вида

г|)'

(|х) =

я])

(j.i)—а

Фо+

(|А)

—

До-

Фо-

(\*)>

где #о± определены формулой (5.5.19), и показать, что i|/ (fx) может

быть представлена в виде

я|>'(|г) = Ji4(v)<D

Gi)dv, (5.5.20)

—1

где A (v) — некоторая функция. Подставляя в (5.5.20) выражение для

Фv(fx) по формуле (5.5.8), получаем сингулярное интегральное урав-

нение

*»

*<l*M<|i)+f

f^,^'-

(5.5.21)

Существование решения этого уравнения докажем, используя ме-

тоды решения сингулярных уравнений, развитые Н. И. Мусхелишви-

ли

[187].

Для этого рассмотрим функцию N

(г)

комплексного перемен-

ного г:

tf(z) = _!_-l Г

v)rfv

, (5.5.22)

2я i 2 J v — z

-1

Она стремится к нулю при | z | -^оо и аналитичиа в комплексной пло-

скости с разрезом вдоль действительной оси от —

до 1.

Пусть Ы

([х) = N (|я ± Ю) при (л g [— 1, 1]. Тогда из формул

Сохоцкого—Племеля [112] следует, что

Д1 2 J V — \i 22

Следовательно,

+ N

-=±p f^

^^A/+-Af-=yMM> (5*5.23)

и уравнение (5.5.21) приводится к виду

(с/2) ДО' (\i) =

[A,

([i)+nc^/2]

N+

(и-)—[А,

([*)

—i«qx/2] ЛГ(ц). (5.5.24)

Введем в рассмотрение функцию Q (г):

)=-!-f Г-^

2я

2 J jx —-2

Она имеет те же свойства, что

функция

N(z),

но стремится к

—

с/(2л\)

при |z| -►оо, а при ц £ [— 1, 1]

Q(v>±iO)

= ——— \iP [-*£-±±-°-р

ч vr/ ^vr-L> у

2п

г j ^,_^ J.

2 2

л i 2

|л'—fx

Из (5.5.14) следует, что

(|г) = 1 + ш (Q+ + Q-); Jiiqx/2 - ш (Q+

—

Q-),

Поэтому интегральное уравнение (5.5.24) превращается в уравнение

-J-H» = [l + 2niQ+(|i)]iV+((i)—[l+2KiQ-(^)]yV-(fx). (5.5.25)

Наконец, рассмотрим функцию

) = [l + 2niQ(

)]^V(

) L_ f^jOi^iJil.

2я i J 2

JA'—z

Она стремится к нулю, при |z| ->-оо и является аналитической во

всей плоскости комплексного переменного, исключая, может быть, от-

резок действительной оси —l^z^l. Но согласно (5.5.25) при

И € [-1, И

F+ (ii)

= F- (ц) = [1 + 2riiQ+] iV+ —

+ 2mQ~] Л/- —

(с/2)

до' (ц) = о,

поэтому функция F

(г)

аналитична всюду. А поскольку на бесконеч-

ности она равна нулю, F

(г)

= 0. Следовательно,

(г)

+2л

i Q (г))-1

-V f -£- HWW .

.5.2б)

—1