Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов
Подождите немного. Документ загружается.


В этом случае
v при 1ф0\
Л/(%
/) =
h
2
(v)+ -2^1v
2
|v при vet
—1,
1]; / = 0;
(—-
— )
при
v
=
v
0
,
/
= 0.
V
vg —1 vl )
cvl
§ 5.7. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ САМОСОПРЯЖЕННОГО
УРАВНЕНИЯ
Найдем [121] решение
и(х
у
Я, й
0
) типа функционала, удовлетворяю-
щее уравнению
— [lQV]
2
u
+
u
=
Su
+ 8(Q, й
0
)б(х). (5.7.1)
Здесь Й
0
£й, б (й, Й
0
)
—
б-функция на Q, нормированная условием
S[/(Q')6(Q',Q
0
)W(Qo),
з
б (х) = П б (xt), где б (xt)
—
одномерные б-функции.
Пусть Su = S[g (Й, Q') и (х, О')] и 0 < g (Й, Й') < 1. Удобно
находить не само фундаментальное решение (5.7.1), а его преобразо-
вание Фурье.
Пусть функция
>(v,
Й)
=
Ф*/
=
Г
и ехр(
—
ivx)d#
является преобразованием Фурье для и. Тогда, умножая (5.7.1) на
exp (— ivx) и интегрируя по R
3t
убеждаемся, что w удовлетворяет
уравнению _
[l + (^v)
2
/
2
]^ = S^+6(Q, Й
0
). (5.7.2)
Решение (5.7.2) ищем в виде
w{v, Й,
Й
0
)
= (1+(Йу)
2
/
2
)"
1
(5(у, Й,
Й
0
)
+ б(Й,Й
0
)), (5.7.3)
где В = В (v, й, й
0
) — неизвестная функция. Подставляя (5.7.3)
в (5.7.2), находим, что В должна удовлетворять интегральному урав-
нению
B(v, Й,
Q
0
)
= S[g(Q, fi')(l+(vft')
2
/
2
)-
1
5(v, Й',
Й
0
)]
+
+ g(Q,Q
0
)[l+(vQ
0
)4*]-\ (5.7.4)
в которое величины v, й
0
входят в качестве параметров. Вследствие
наложенных ограничений на g (й, й
0
) уравнение (5.7.4) для всех
v 6 #з> ^о 6 й имеет, и притом единственное, решение. В случае,
когда функция g (й, Й') имеет вид
вг(0,о')= S
МО)
мщ.
/= 1
90
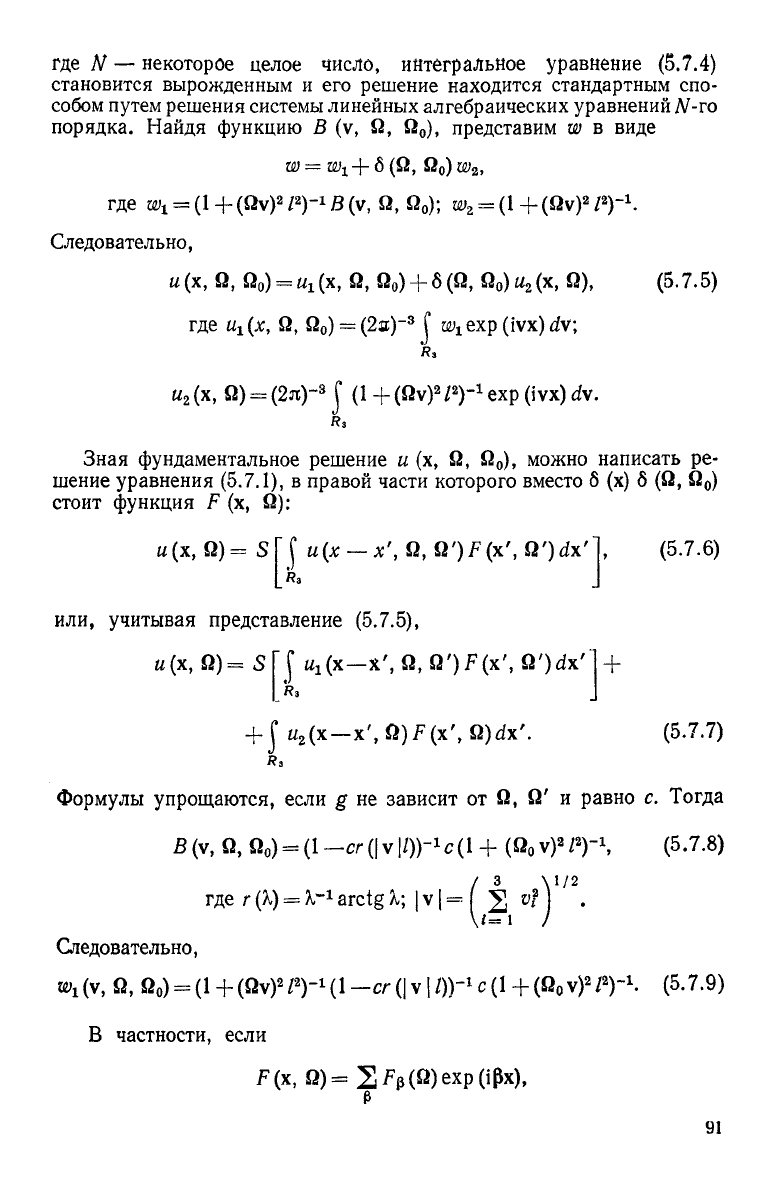
где N — некоторое целое число, интегральное уравнение (5.7.4)
становится вырожденным и его решение находится стандартным спо-
собом путем
решения
системы
линейных алгебраических уравнений
N-TO
порядка. Найдя функцию В (v, й, й
0
), представим w в виде
w=w
1
+8(ii
y
й
0
) w
2
,
где щ =
(1
+
(Йу)
2
Z
2
)-
1
В
(v,
й, Й
0
);
w
2
=
(1
+
(Йу)
2
Р)'
1
.
Следовательно,
и(х, й,
Й
0
)
= ^(х, Й, й
0
) +
б(Й,
Й
0
)и
2
(х, Й), (5.7.5)
где и
г
(х, Й,
Й
0
)
=
(2я;)-
3
Г
w
t
exp
(ivx)
dv\
Яз
и
2
(х,
Й)
=
(2я)~
3
J
(1
+
(ЙУ)
2
Z
2
)-
1
exp
(ivx) dv.
Зная фундаментальное решение и (х, й, й
0
), можно написать ре-
шение уравнения (5.7.1), в правой части которого вместо б (х) б (Й, й
0
)
стоит функция F (х, й):
и(х, Й)= S
f и(*
—
х\ Й, й')^(х', Й')<*х'
(5.7.6)
или, учитывая представление (5.7.5),
*/(х,
Й)= S
+
(5.7.7)
*f ^(х—x'
f
G,Q')F(x'.
°')^х'"
+ f «
2
(х—х', Q)F(x\ Q)dx'.
Rs
Формулы упрощаются, если g не зависит от Й, Й' и равно с. Тогда
В
(v,
Й,
Й
0
)
=
(1
-сг
(|
v
Ю)-
1
с (1
+
(Йо
v)
2
Р)~\ (5.7.8)
rAer(X) = ^arctgX;|vH^2 ^У"-
Следовательно,
щ(у, Й, Й
0
) = (1+(ЙУ)
2
/
2
)-
1
(1-^(^|/))""
1
С(1+(Й
0
У)
2
/
2
)-
1
. (5.7.9)
В частности, если
F(x
f
Q)=2^Wexp(iPx)
f
91

где
р _ некоторая последовательность трехмерных векторов, то
и(х,
О)
= 2 (I +
/"
(OP)
1
)"
1
[c/?J (1 —сг
(/1
р
|))-i +
э
+ F|,(Q)]exp(ipx), (5.7.10)
где П = 5[^(Й')(1+/
2
ФЙТГ
Х
]-
В работах [121, 130] аналогичные формулы получены для много-
групповых задач в ^-мерных пространствах.
§ 5.8. 2яГ-ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
Получим формулы для решения в ячейках различной формы
[121].
Такие решения формально можно Описать следующим образом. Пусть
Т
—
трехмерная матрица и det Т Ф 0. Обозначим п = (п
ъ
п
ъ
п
3
) —
вектор с целочисленными компонентами; пусть х = 2дГу, где х,
у £ R
3
. В R
3
отождествим все точки, отличающиеся друг от друга на
векторы вида 2яГп. Полученное многообразие всех эквивалентных
то-
чек представляет собой трехмерный тор Г
3
, который называется фун-
даментальной областью для 2яГ-периодических функций. Так назы-
ваются функции ф (х), для которых при любом х и любом целочислен-
ном п справедливо равенство ф (х)= ф (х + 2пТп). При помощи раз-
резов тор Т
3
может быть превращен в односвязную область, и притом
разными способами, например, в куб— 1/2 ^ y
t
^ 1/2, i = 1, 2, 3.
Нахождению 2яГ-периодических решений для полигармонических
уравнений посвящены исследования С. Л. Соболева
[220].
Найдем на Т
3
решение уравнения
—
[/«Vl
2
и + и = cSu + F (х, Q), (5.8.1)
в котором для простоты считаем / и с <
1
постоянными. Эта задача
является идеализированной для ячеек реактора, форма которых
определяется матрицей Т (например , плоских, кубических, шести-
гранных). Для нахождения решения 2я7'-периодической задачи ис-
пользуем метод, изложенный в работе
[121].
Условимся в формулах
суммирования по п не ставить индекс суммирования. Пусть Т* обоз-
начает сопряженную к Т матрицу. Предположим, что функция F (х, Q)
разлагается в ряд Фурье:
F(x,Q) = 2F
n
(Q)exp(i$
n
x), (5.8.2)
где р
п
= (Г""
1
)* п; пусть
^n^lPnl/^^r^J^^^arctg^; О
п
(Й) = (1+(Р
п
Й)
2
/
2
)"
1
. (5.8.3)
Решение задачи (5.8.1) имеет вид
a = 2g
n
(Q)exp(ip
n
x). (5.8.4)
Подставляя (5.8.4), (5.8.2) в (5.8.1) и приравнивая коэффициенты
при функциях exp (iP
n
x), получаем для определения g
n
(£i) уравнения
(1 + (№)
2
l
2
)gn(®) =
cSg
n
+
F
n
(Q).
(5.8.5)
92

Решение (5.8.5) ищем в виде
g
n
(Q)
=
(1
+
<р
п
О)»
l*)-
1
(В
п
+
F
n
(Q)).
(5.8.6)
Обозначая
/
7
J=S[(l + (p
n
й')/
2
)-
1
^
7
n(^
,
)]
и учитывая, что
S[(i+(p
n
a')
2
/
2
)-4=r(lp
n
|/),
из (5.8.6) получаем
Sg
n
= г
п
В
п
+ П, (5.8.7)
или,
подставляя (5.8.7) и (5.8.6) в (5.8.5), В
п
= с (r
n
B
n
+ FJ), т. е.
B
n
=(l-crJ-*cFl
Далее, поскольку в обозначениях (5.8.3) и записывается в виде
и = 2G
n
(Q) (B
n
+ FJ ехр (ф
п
х),
имеем
а = SG
n
(Q) (1
-crj-
1
cFJ +
F
n
)
ехр (ф
п
х).
(5.8.8)
Применяя к и операцию S, нетрудно убедиться, что
Su = 2
((1
-crj-
1
F£ ехр (ф
п
х),
(5.8.9)
где для изотропного источника
F\ =
r
n
F
n
.
(5.8.10)
Полученная формула (5.8.8) при {$ = {0
П
} совпадает с формулой
(5.7.10).
Заметим, что в (5.8.8) отсутствуют члены, являющиеся реше-
ниями однородной задачи (5.8.1). В работе [121] получены решения
периодических многогрупповых задач в случае, когда элементы ма-
трицы с зависят от х.
Приведем примеры матриц Т: единичная матрица определяет квад-
ратную ячейку, а матрица
(УШ ° о
Т =
Щ
1/2 10
\ 0 0 1
— шестигранную (рис. 5.4).
На рис. 5.5 приведены качественные результаты расчета В.И. Агош-
ковым шестигранной ячейки при / = 0,92, с = 0,7 и единичном ис-
точнике в центре. Другие способы расчета четырех- и шестигранных
ячеек описаны в §6.6, 6.7, 6.9.
Мы получили в явном виде решения ряда задач. На некоторых
из этих задач будем проверять эффективность аппроксимации разност-
ных методов и эффективность итерационных методов решения задач
93

переноса. В этом отношении особенно удобна 2я-периодическая зада-
ча с постоянными /, с, ибо для разностных методов в таком случае уда-
ется получить неулучшаемые по порядку малости оценки погрешности
решений разностных уравнений. А для итерационных методов эта кра-
евая задача удобна тем, что для нее простые итерации сходятся
*2>У2
Рис. 5.4. Шестигранная ячейка Рис. 5.5. Общий вид нейтронного
поля и
0
(х)
наиболее медленно и, следовательно, эффективность многих методов,
ускоряющих процесс простой итерации, наиболее четко определяет-
ся именно на периодических задачах.
Решения, полученные в данной главе, целесообразно использовать
в различных приближенных методах (типа Галеркина и др.) по реше-
нию задач с переменными коэффициентами (см. §6.9).
§ 5.9. КВАДРАТУРНЫЕ ФОРМУЛЫ ДЛЯ СФЕРЫ
При решении задач переноса в общей геометрии необходимо иметь
достаточно точные квадратурные формулы для сферы с положитель-
ными весами для аппроксимации интегральных операторов уравнения
переноса. Изложим кратко описание метода получения квадратурных
формул типа Гаусса для единичной сферы, инвариантных относитель-
но группы вращения октаэдра с инверсией GI и точных для всех мно-
гочленов степени п включительно
[138].
Максимальная алгебраиче-
ская точность п таких квадратур достигается путем специального вы-
бора узлов и весов. Очевидно, что такие квадратуры будут обладать
меньшим по сравнению с обычным числом узлов N.
Пусть в R
3
(х, у, г) задана единичная сфера Q: х
2
+ у
2
+ z
2
= 1,
а V — вписанный в нее октаэдр, вершины которого лежат на осях
координат. Пусть
J(/)=
i!rI
/(Q)da
(5.9.1)
94

Квадратуру для интеграла (5.9.1) будем искать в инвариантном отно-
сительно группы GI виде:
5(/) =
Л 2 f(flt) +
A
t
2 f(a?) +
A
3
2 /(<*?) + S
5
" 2 /(#) +
<=i г=1 /=i k=i t=i
N
'
2i
С, Ьч
N
»
48
/ Ьч
+ 2
с
* 2
;
(
с
*)+ 2^11
/(<#).
(5.9.2)
где Л
fe
, Вь, Ch, D
fe
— веса квадратурной формулы, а координаты на
Q характерных узлов квадратуры каждого типа имеют вид
а\ = (1,0,0); af = (2-
1
/
2
,2-
1
/2
i
0); a? =
(3~
1
/
2
,
3"»/^ 3^/2);
*i =
Слэ
/л» m
h
)\ c\ = (p
ft
, ^ft, 0); d\ = (r
fe
,
s
fc>
w
h
)
(2ll + ml^U pl + ql=U r
k
+ sl + w%=\).
Остальные узлы каждого типа получаются из приведенных переста-
новкой координат или изменением у них знака.
Веса и узлы в формуле (5.9.2) подберем такими, чтобы равенство
J(f) = S (/) (5.9.3)
выполнялось для всех многочленов / до возможно наибольшей степе-
ни п. Согласно теореме С. Л. Соболева
[221],
для этого достаточно тре-
бования, чтобы равенство (5.9.3) было выполнено лишь для всех ин-
вариантных относительно группы GI многочленов. А так как любой
инвариантный относительно
G%
многочлен представим на й в виде
многочлена от а
2
=
х
2
у
2
+ x
2
z
2
+
y
2
z
2
и а
3
= x
2
y
2
z
2
, то достаточно
потребовать, чтобы равенство (5.9.3) было выполнено для всех много-
членов Q (а
2
, а
3
) из множества Т
пу
которое определено требованием,
чтобы степень Q в переменных х, у, z не превышала я. Подставляя в
(5.9.3) все линейно-независимые многочлены Q £ Т
пу
получаем си-
стему нелинейных алгебраических уравнений для определения весов
и значений o
2k
,
a
3ky
соответствующих узлам квадратуры. Методы
решения таких систем описаны в работах [138, 139].
Приведем таблицы нескольких квадратур типа (5.9.2); в них N —
общее число узлов, а п
—
алгебраическая точность.
м= 11
N = 50, Nx = 1, N
2
= N
3
= 0 (слагаемые с C
h
и D
k
отсутствуют),
А
г
= 4/315, А
2
= 64/2835, А
3
= 27/1280,
В
г
= 11
4
/725760, т
г
=
3/J/Tf,
h =
1/]/ТТ.
п= 15
# = 86,^ = 2, W
2
=l, N
3
= 0
y
Л
2
= 0,
А
г
= 1,1544011544Ы0"
2
, А
3
= 1,19439090859 . 10~
2
,
В
г
= 1,11105557106 • Ю-
2
, В
2
= 1,18765012945. Ю-
2
,
С
г
= 1,18123037469-Ю-
2
,
1
г
= 0,369602846454, т
1
= 0,852518311701,
/
2
= 0,694354006603, т
2
= 0,189063552885,
Рх = 0,927330657151, ?i = 0,374243039090.
95

Веса этой квадратуры хорошо выравнены.
п
= 17
N
=
ПО,
^ = 3,
JV
2
= 1,
А
х
=
3,82827049494-Ю-
8
,
А
8
=
В
х
= 8,21173728319-10"
8
, 5
2
=
В
8
= 9,94281489118-Ю-
8
, С
х
=
/
2
= 0,185115635345, т
х
=
/
2
= 0,395689473056, т
2
=
/
3
= 0,690421048382, т
3
=
Pi = 0,878158910604, ft =
#
3
= 0, Л
2
= 0,
9,79373751249-Ю-
3
,
9,59547133607-Ю-
3
,
9,69499636166- Ю-
8
,
0,965124035087,
0,828769981253,
0,215957291846,
0,478369028812.
п = 23
JV
= 194,
ЛГ!
= 4, JV
2
Л
х
= 1,78234044724-Ю-
8
,
Л
2
;
А
з
==
5,57338317884
•
10"
8
,
C
t
--
В
х
=
5,51877146727-10"
3
,
5
2
=
5
3
=
5,60870408259-Ю-
3
,
В
4
Dj
=
5,53024891623
•
10"
3
,
г
г
=
«!
=
0,159041710538,
^
=
Рх
=
0,938319218138,
^
/
х
=
0,444693317871,
т
х
/
2
=
0,289246562758,
от
2
■■
1
г
=
0,671297344270,
от
3
U
=
0,129933544765,
от
4
=
=
1,
N
s
=l,
=
5,71690594998-Ю-
3
,
=
5,05184606462-Ю-
3
,
= 5,15823771181-Ю-
8
,
= 4,10677702817-Ю-
8
,
= 0,836036015482,
= 0,525118572443,
= 0,345770219761,
= 0,777493219315,
= 0,912509096867.
= 0,314196994183,
= 0,982972302707.
В работах
[139]
опубликованы квадратура 29-го порядка,
для нее
N
=
302,
и
35-го порядка,
для нее N =
434.
Узлы квадратур
для
п
= 11, 17, 23, 29, 35
правильно триангулируют поверхность сферы.
Для некоторых задач теории переноса при решении могут нарушать-
ся условия гладкости вдоль некоторых поверхностей, например,
в за-
дачах,
в
которых коэффициенты
и
источник терпят разрывы
на
поверх-
ностях, параллельных координатным плоскостям.
В
этом случае
в
разностной схеме желательно
не
употреблять угловые направления,
вдоль которых распространяются разрывы
в
решении.
В
работах
Карлсона
[94] был
предложен способ построения квадратур этого типа
для 5
т
-метода, однако алгебраическая степень точности
п
таких квад-
ратур сравнительно невелика.
Ее
можно существенно улучшить,
не
меняя общего числа узлов квадратуры, если искать квадратуры типа
Маркова—Гаусса вида (5.9.2), считая
в ней Л
х
= Л
2
= C
h
= 0, а
другие параметры
—
подлежащими определению.
Приведем таблицы узлов
и
весов квадратур такого типа.
N
= 48, Nt = 2, N
2
= N
a
= 0, A
s
= 0,
B
x
=
2,22694087831
•
Ю"
2
,
В
г
=
1,93972578836-10~
2
,
/
х
=
0,68177989763,
/Пх
=
0,265240161182,
/
2
=
0,241542018852,
от,
=.0,939848342159.
96

п = 11
N = 56, N
t
= 2, N
2
= N
3
Bx = (122 — 9J/3)/(2
e
-105), B
a
=
/
x
= (3 + 4//3)'/
2
/KH, /
2
л = 19
= 0, Л
3
= 9/560,
= (122 + 9l/3j/(2
e
-105),
= (3
—4/^3)'/
2
/11.
= 0, N
3
=l,
= 7,66142612552-10"
3
,
6,07598203150XlO"
3
,
=
6,99108735330-lO"
3
,
=
0,975843959536,
=
0,810512740174,
0,330816636714,
0,101617454410,
0,882270011260,
между n и N для квадратур
N = 152, Ni = 4, #
a
A
3
= 6,15916486467-lO"
3
, B
t
=
B
2
= 6,63204497655-
lO"
3
,
B
3
=
B
4
= 5,26198387161
•
10"
3
, D
r
=
/x = 0,154480689145, m
x
=
l
%
= 0,414167295917, от
2
=
l
3
= 0,667293171280, m
3
=
U = 0,703446477338, m
t
=
r
x
= 0,449332832327, s
t
=
a»!
= 0,140355381171.
Для сравнения укажем соотношения
Sm-метода: если
от = 8, то п = 9, JV = 80;
от = 10 — л = 11, N = 120;
т
= 12 — л = 11,
W
= 168;
от = 24 — п = 19, # = 624;
от = 26 — п = 19,
JV
= 729.
Для от ^ 24 у этих квадратур появляются отрицательные веса. Как
видно из приведенных данных квадратуры типа Маркова—Гаусса,
при заданной алгебраической степени точности л имеют существенно
меньшее число узлов.
В дальнейшем изложении удобнее будет не дифференцировать веса
и узлы квадратуры по типам, как это сделано в формуле (5.9.2), а вве-
сти единые для них обозначения w
m
и
Q"»
соответственно. Тогда квад-
ратурная формула (5.9.2) запишется в виде
S(f)
=
N
ет=1
w
m
f(Q>"). (5.9.4)
97

МЕТОДЫ АППРОКСИМАЦИИ
Глава
МЕТОД СФЕРИЧЕСКИХ
ГАРМОНИК, МЕТОД
ГАЛЕРКИНА
§ 6.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕТОДА СФЕРИЧЕСКИХ
ГАРМОНИК
В настоящей главе изложен один из эффективных методов решения
кинетических уравнений — метод сферических гармоник. В разра-
ботке метода сферических гармоник принимали участие С. Чандра-
секар
[238],
Вик [344, 345], Р. Маршак [310, 311], Г. Бете, Л. Тонкс,
Г. Гурвитц
[259],
Б. Дэвисон [81], Дж. Марк
[308],
В. С. Владимиров
[41] и другие [162, 169]. Метод сферических гармоник является по
существу методом Галеркина при специальном выборе базисных функ-
ций и состоит в том, что приближенное решение (Р
п
-приближение)
ищется в виде
ф
(">(х,Й)= 2(2*+1) S Фм(х)П|(0). (6.1.1)
где ум (х) — неизвестные функции. Выражения для ф
(п
> подставля-
ем в кинетическое уравнение (5.1.4), затем полученное выражение по-
следовательно умножаем на Y
lm
, т = 0, ± 1, ..., ± /; / = 0, 1,..., я,
и к результату применяем оператор S. В итоге получаем, вообще го-
воря, (п + I)
2
уравнений в частных производных относительно функ-
ций
<p
ki
(х). Система уравнений дополняется граничными условиями,
которые приближенно учитывают граничные условия исходной зада-
чи.
Выясним структуру получающейся при этом системы дифферен-
циальных уравнений. Оператор 5ф
(п)
можно вычислить непосредствен-
но,
пользуясь формулой (5.1.36):
S<peo = S*q><«>= S(2A+l)**(x) S Vki(x)Y
hi
(Q), (6.1.2)
&=o
/=—
k
где
l
gh =
gk
(x) = у J g (x,
\i)
P
h
(Ц)
d|x. (6.1.3)
—
i
Поэтому
S[{X<fW-2
8
SifW-f)Y
lm
] =
= (2/+l)S, „J-^ll . <Ptm(x)-/|
m
, (6Л.4)
(/
+ |m|)!(i-|-o
om
)
где f
lm
= S
(fY
lm
);
2, = 2-g,2
s
.
98

Обозначая ср, /совокупность функций
{ф^
ш
},
{Am}, / = 0, 1, ..., я,
№
= — /,..., О, ..., /, систему дифференциальных уравнений можно
записать в матричном виде
з
/==1
2^-^7 +
£>(х)
Ф
=
/.
(6.1.5)
Здесь матрицы L,-, i = 1, 2, 3, не зависят от координат х, a D — диа-
гональная матрица с элементами, определяемыми формулой (6.1.4).
Выясним структуру матриц L
u
которые получены в результате вы-
числения следующей величины:
K--=S(Y
lm
SlVq^) =
= 2
2<
2
*
+ 1)
2
S(Y
im
Y
hJ
Q
t
)*>$l£L.
t= 1/2 = 0 /=_fe ^
l
Пользуясь ортогональностью сферических функций, получаем
ffl
L
jj\-l
axi
+ (2/+l) 2 S(K
jM
y
w
Q,)-2!^- +
+
(2/
+
3)
^ 5(r
im
7
w
,
7
.Q0^HiiW.]. (6.1.6)
/=-/-1 ** '
Поскольку 5 (Y
lm
Yu^i) = 0, второй суммы в (6.1.6) не будет.
Следовательно, матрицы L
t
являются блочно-двухдиагональными ма-
трицами с нулевой диагональю. В работе И. А. Адамской [11] подроб-
но исследована структура блоков матрицы L
t
и получен вид (6.1.6)
для ортогональных криволинейных координат.
В.
С. Владимиров показал для нечетных я, что при выполнении
(5.1.6) для произвольной невогнутой области D в качестве граничных
можно принять следующие условия:
J dQQncpW (г, Q)
Y
2ky
m
(О) = 0 на Г, (6.1.7)
Qn<0
= 0, 1, 2, ...; т = 0, ± 1, ± 2, ..., ± 2k.
Граничное условие (6.1.7) получено из вариационного принципа
для случая четной индикатрисы рассеяния [41, 42]. В дальнейшем
будем пользоваться аналогичным принципом для произвольной инди-
катрисы рассеяния и условий (5.3.6). Математическое обоснование ме-
тода сферических гармоник, вопросы сходимости его рассмотрены в
работах В. С. Владимирова [41].
99
