Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов
Подождите немного. Документ загружается.


§ 6.2. ПЛОСКОПАРАЛЛЕЛЬНЫЕ И СФЕРИЧЕСКИ-СИММЕТРИЧНЫЕ
СИСТЕМЫ
Рассмотрим кинетическое уравнение переноса нейтронов (5.2.8)
в плоскопараллельной геометрии; предполагается, что в нем функции
/ (z, fi) и
ф
(z, \i) не зависят от азимута
i|).
Решение будем искать в виде
ряда
Ф(*.
rt= 5 (2A+l)<Pik(*)P*(|i). (6.2.1)
Подставим (6.2.1) в уравнение (5.2.8) и воспользуемся первыми
рекуррентными соотношениями (5.1.31) и формулами (6.1.2), (6.1.3),
умножая затем полученное выражение на Р
т
(\i)
и интегрируя ре-
зультат по [—
1
^ |х ^ 1], получаем для функций ф
т
(г) систему ли-
нейных дифференциальных уравнений
m
^i
+
(m+1)
*^i
+ (2/n+1)S ф
dz dz
= (2m+l)/
M
(z)
(от
=
0,
1,...),
(6.2.2)
где
I
fm (Z)
= у J /
(Z,
V)
P
m
((I)
<*|i.
(6.2.3)
— 1
Введем в рассмотрение вектор-столбцы
Ф
=
[ф2го1>
^=[?Sm+l].
/ = [(4т +
1)
/
2т
],
F
= [(4т +
3)
/,
т+1
]
(т =
0,
1,2,...),
(6.2.4)
матрицы
а
/1 0 0 0
' 2
1
+
2
0
0
=\ 0 2-2
1
+ 2-2 0
1
0 0
2-3
1
+ 2-3 ...
/1 2 0
0
/0
1
+
2
2-2
0
р=
= 1
0 о
1
+ 2-2
2-3 ...
10 0 0
1
+ 2-3 ...
(6.2.5
и диагональные матрицы
а = diag
[(1
+ 4m) 2
2
J; b = diag [(3 + 4m)
2
2m+1
].
(6.2.6)
Тогда система уравнений (6.2.2) в матричной форме примет вид
adJIdz + аф = /; p^p/dz + bJ = F. (6.2.7)
100

Рассмотрим вопрос
о
граничных условиях
в
приближении метода
сферических гармоник. Пусть точное граничное условие имеет
вид
Ф
(0, |я) = 0 при ц > 0;
(6.2.8)
Ф
(Я, [х) = 0 при |л< 0.
(6.2.9)
Р.
Маршак
[310, 311]
предложил
для
получения требуемых гра-
ничных условий заменить, например, (6.2.9) системой интегральных
соотношений
[см.
также
(6.1.7)1:
о
f Л*т(ц)Ф^
=
0
при
z=H{i
=
0,
1,2,...).
(6.2.10)
-
J
i
Подставляя решение
в
виде ряда (6.2.1)
в
соотношения (6.2.10),
приходим
к
бесконечной системе алгебраических выражений
S
a
i»<?m
= ° (/ =
0,1,2,...), (6.2.11)
m = 0
где
о
а
гга
=
(2т+1)
J
P„+i0i)/>™0i)d|i
(/ =
0,1,2,...). (6.2.12)
— 1
В.
С.
Владимиров показал,
что
этот способ аппроксимации граничного
условия (6.2.9)
в
известном смысле является наилучшим
[41].
Однородную систему уравнений (6.2.11) запишем
в
векторно-ма-
тричной форме
Жр
+
C
J = 0 при z = Я,
(6.2.13)
где
m
=
0,2,
4,... J
lm
m=l,3,5,...
j
Точно
так же
граничное условие (6.2.8) заменяется равенствами
1
^21+1(^)ф^
= 0 при
z
=
0
(t =
0,1,2,...).
о
Если область
D и
источники симметричны относительно плоскости
z
= 0, то на
этой плоскости необходимо поставить условие
d(t>/dz
= 0 при 2 = 0.
(6.2.14)
Аналогично изложенному аппроксимируются краевые условия
(5.2.11).
Отметим,
что нас
интересует только непрерывное
во
всем объеме
D решение задачи.
Это
значит,
что при
переходе
из
одной зоны
в
дру-
гую
с
разрывом физических констант
на
границе раздела имеет место
непрерывность всех компонент решения
ф
т
(г).
101

Переходим к рассмотрению сферически-симметричных задач. Со-
ответствующее кинетическое уравнение
в
этом случае имеет
вид
(5.2.16).
Пусть
Ф
(R,
\х)
= 0 при
\х
< 0. (6.2.15)
Решение уравнения (5.2.16) будем искать в виде
Ф(М*)= 2 (2*+1)Ф*(г)Р*(|1).
(6.2.16)
fc
= 0
Подставим (6.2.16) в уравнение (5.2.16), воспользуемся вторым рекур-
рентным соотношением (5.1.31) и равенствами (6.1.2), (6.1.3). После
этого, умножая полученное выражение на Р
т
(\i)
и интегрируя ре-
зультат
по
[—
1
< \i < 1], получаем для функций ф
т
(г)
систему обык-
новенных дифференциальных уравнений:
dr г
+ (2т+1)2
т
ф
т
= (2т+1)/
те
(г),
(6.2.17)
где /
т
(г) — коэффициенты Фурье функции / (г, |i), определяемые ра-
венством (6.2.3).
Систему уравнений (6.2.17) преобразуем к виду
mr
m-l JLJ!2!zi. + (m+l)
l
,m—1
r
m+2
<Pm+i +
+ (2m+l)2
m
cp
m
= (2m+l)/
ro
. (6.2.18)
С помощью векторов ф, J,f,Fu матриц а и
Ь,
определенных выше,
систему уравнений (6.2.18), запишем в векторно-матричной форме:
KJ +
а<р
= /; L(f + bJ = F, (6.2.19)
где К и L
—
операторы, определенные следующим образом:
1
К
=
L =
\
1 а 2
0 0 0...
2гА-±
dr г
3
Г
4
0
0...
0
4/-з
d J_
dr r
3
5 d
re dr
-r
6
0...
d 2 d
dr г
3
dr
г
3
0
0
-1
0
3r
2
—
dr
1
Г*
r* dr
-r
5
0
...
0 0
5r*-A_
dr
1 _6_
r
4
r
7
d
dr
r
7
...
... ... ••
*'* _
102

К системе уравнений (6.2.19) необходимо присоединить граничные
условия. Именно, в центре сферически-симметричной области / = О
при г = 0, на внешней границе области из условия (6.2.10) получаем
dtp
+ cJ = 0 при г = R.
§ 6.3. БЕСКОНЕЧНЫЕ ЦИЛИНДРИЧЕСКИЕ СИСТЕМЫ
Рассмотрим бесконечные осесимметричные цилиндрические систе-
мы.
Пусть ось z совпадает с осью симметрии цилиндра. Тогда основное
кинетическое уравнение переноса нейтронов запишется в виде (5.2.21),
а граничное условие — в виде (5.3.6).
Решение этой задачи представим в виде ряда по сферическим функ-
циям
ф(г,Ч>,*)= 2 (2л+1)Ф„о(г)Р„(т) +
+ 2 У У (2/2+1)-£^L
фпт
(г)cosтф/tf(
7
), (6.3.1)
где Рп (у) —присоединенные функции Лежандра, у = cos*.
В разложении (6.3.1) учтено, что функция ф (V, if, ft) четная отно-
сительно угла1|?. Подставим ряд (6.3.1) в уравнение (5.2.21) и преобра-
зуем слагаемые полученного выражения. Так, сначала преобразуем
первое слагаемое
sin ft cos
i|)
— = V
(2м
+
1)
ф„
0
(r) cos
г|э
sin ftP„ (cos ft) +
/г = 0
00 tl
+ У У(2п + 1) i"~
m
||
Ф™
(r)
[COS
(m-1)
Ч>
+ cos
(m
+
1) ф]
x
X sinftP,7(cosft). (6.3.2)
Принимая во внимание соотношение
sin
ftP™(cos
ft)
= ! [P^i (cos ft)-P^i
1
(cos ft)] =
2я+1
[(/i +
m) (n
+ m—
1) P™+
i
l
(cos
i
-{n—m+l)(/i—m + 2)P
/
T4T
1
1
(cosft)], (6.3.3)
выражение (6.3.2) приведем к следующему виду:
<*L
-= V V m' . м (я—m)!
х
(п + т —
2)!
sinftcosi|)-^.= 2 2фп~1.ш-1(0~
оо /t-f-2
xP*(cos<>)cos/m|>— ^ 2
*« +
1
-«-iW
(я-т +
2)!
х
(я +
т)!
я =
— 1
щ =
1
103
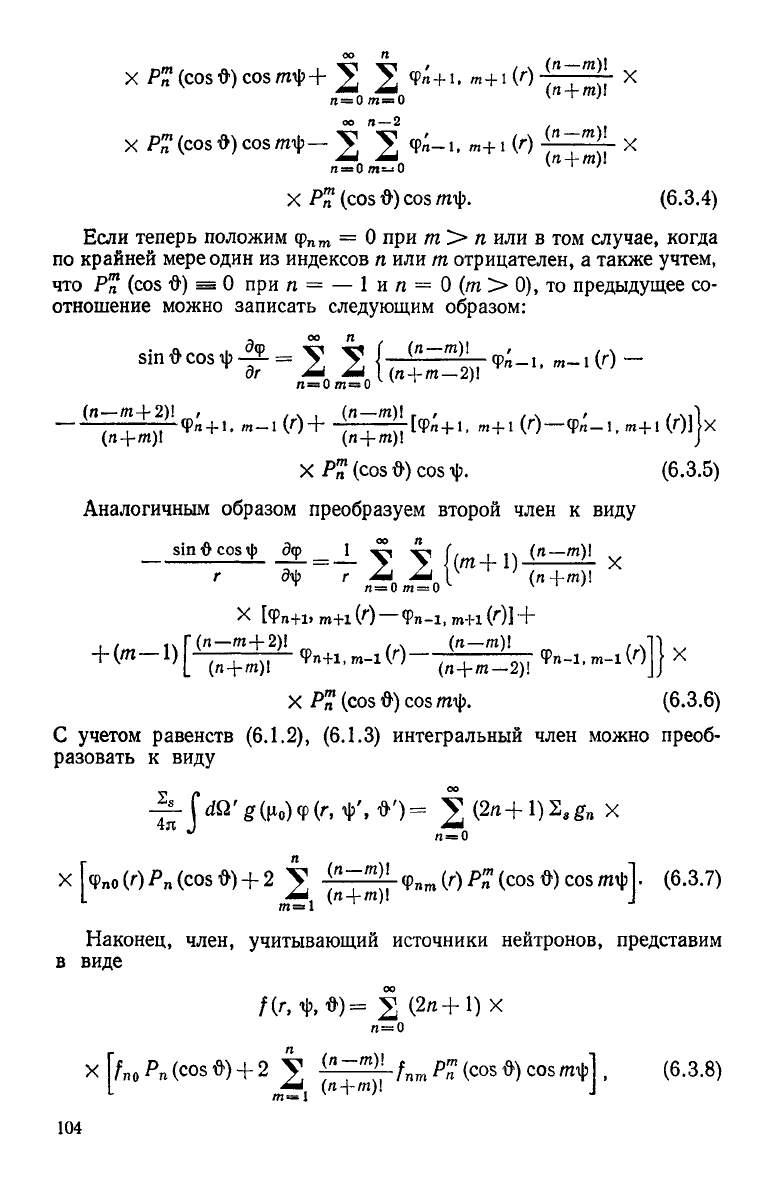
x Pj?(cosd)cosmt|> + 2 2
ф
"+
1
'
т+х{г)
^Ь^
Х
оо Л —2
(л
—
т)\
X Р*
(cos Ф) cos
тф. (6.3.4)
Если теперь положим
cp
nm
= 0 при т> п или в том случае, когда
по крайней
мере один
из индексов п или т отрицателен, а также учтем,
что Рп (cos #)s0 при п = —
1
и я = 0 (т >0), то предыдущее со-
отношение можно записать следующим образом:
фА
+
1.
m-1 (0+ ^T^l [Фп+l, т+1
(Г)
—фя-1,
«+I (
Г
)]]х
(п +
т)!
X/^(cos#)cos\|). (6.3.5)
Аналогичным образом преобразуем второй член к виду
sinЬcosi|? ^Ф
=
J_ V< у f/
m
|
п
(я—m)l
г дф г Л
п
^Д (я+т)!
X [ф
п
+1,«+х(0 — Фп-1,т-ы(0] +
, /
1\Г(
Я
—яг
+
2)!
/ч
(м—т)! ,
Ч
"П
w
xP»(cos#)cos/m|). (6.3.6)
С учетом равенств (6.1.2), (6.1.3) интегральный член можно преоб-
разовать к виду
4я
J
п = 0
Х[Ф„О(Г)РП(СО
8
*)
+ 2 У il^
Vnm
(r)/>?(cos*)cosm4
(
6
-
3
-
7
)
Наконец, член, учитывающий источники нейтронов, представим
в виде
/(',*.*) = 2(2rt+l)X
л=0
хГ/
пв
Р
Л
(со8*) +
2
У ^^/nm^lcos^cosm*], (6.3.8)
104

где
2я
f
nm
= _L Г cos
m^dyp
f /
(г,
г|>, ф) P* (cos 0) sin fldft. (6.3.9)
о о
Собрав все члены, объединив их под знаком сумм и приравняв нулю,
получим бесконечную систему уравнений:
при т =
О
1 d
/•(Фп
+1
.1-Фп-1,1) + (2п+1)2
п
ф
п0
:=(2Аг+1)/
п
о; (6.3.10)
г dr
при
т
^
1
г"-
1
-^-г«-*[(я + т+1)(» + т + 2)ф
п
_
1|Ж
.
1
-
—(я—т + 1)(л—т+2)ф
п+1
,
т
_
1
] +
+ Г"-> -£-
г
1
+«(ф
п+1
,
т+1
-ф
п
-
1(
ro+
i) +
ах
+ 2(2л+1)2
Л
ф
пт
=2(2я+1)/
пт
. (6.3.11)
Учтем тот факт, что при нашем выборе системы координат функ-
ция ф (г, i|), ft) симметрична по переменной у = cosft. Это значит, что
присоединенные функции Лежандра должны быть четными и, следо-
вательно, сумма индексов п + т всегда должна быть четной.
Для одномерной цилиндрической геометрии, положив
dQ = sin ftdftdty; Qn = sin
О
cos
tj);
(6.3.12)
Y2k,
m
(
Q
) = P& (cos ft) cos
/m|>;
(6.3.13)
Ф (г|>, О) =
q>
(Я, o|>, ft) — x [a — (4 (1 — a)/n) cos\|)] 7ф—
-V
(♦,*),
(6.3.14)
по аналогии с (6.1.7) приходим к граничным условиям
Я Я/2
J dtp j ф(г|), d) P^(cosfl)sin
a
dcosA|>cosi|>dd = 0, (6.3.15)
Я/2 Я
* = 0, 1, 2, ...; / = 0, 1, 2 2й.
Подставляя (6.3.1) в граничное условие (6.3,15) и выполняя вы-
числения, приходим к соотношениям
2в&Фпт = У«П
Р
ИГ =
Я,
(6-3.16)
п,
т
где
ctmn,
V
kt
— некоторые числа.
Система уравнений (6.3.10), (6.3.11) позволяет сформулировать лю-
бое приближение метода сферических гармоник. Для практических
Целей достаточно ограничиться Р
3
-приближением, полагая ф
пт
= 0
105

при п ^ 4. В этом случае будем иметь взаимосвязанную систему для
четных моментов
— гфп + 2
0
Фоо
=
/ось
г dr
г dr
1 d
i
г dr
J_ _£_ фп
г d
2 dr г 12 dr
+ —
2
2Ф22 =
" 12
/22
и для нечетных
dy
00
d(p20
.1 ,
l
— гф
и
+ 5Е
2
ф
20
= 5/
20
;
ф31
1
24r
3
dr
Гфзз+
^ф
2
р
dr
d
2r
2
dr
г
2
ф22
+
32
1ф11
=3/
11;
dr
1 d
9
, 7 YI 7 r
1^^г
г
^
+
Т
2зФз1==
Т
/з1;
^^-^+-^-2
3
Фзз= —/33.
24 dr r
2
360
3Y33
360
/33
Введем в рассмотрение вектор-столбцы
Ф = (фоо, Ф20, Ф22); J = (фш Фзь Фзз)
и операторы
К =
1 d
Tlr~
r
1 d
г dr
г d 1
2 dr г
d
dr
0
0
0
1 d
0
1 d
•r
2
r dr
r d 1
~~ 12 dr r 24r
8
dr
_d_ _J d_
dr 2r
2
dr
d_ ___J d_
2
dr "" 12r
2
dr
Г
r
2
J d 1
24 dr r
2
0
(6.3.17)
(6.3.18)
(6.3.19)
Тогда система уравнений (6.3.17), (6.3.18) в векторно-матричной
форме принимает вид (6.2.19), где
а= diag[s
0
, 52
2
, JL 2
2
]; Ь = diag [32
Х
,
-^-2
3
,
-JL Ц А
f =(/оо> 5/
2
о, —^ /22j"» ^=(3/и> "^г/з1>
~£jjjjj"
/зз|.
(6.3.20)
106

(6.3.21)
Переходим теперь к обсуждению вопроса о граничных условиях.
Полагая в (6.3.15) k = 0, / = 0, а затем k = 1, / = 0,2, получаем,
что при г = R
—(1—х)(16ф
00
—
10ф
2
о
+
5гр
22
)
+
32(1
+
х)
ф11
=
8Уоо;
5
(1-х) (8ф
00
-"50ф
2
о+5ф
22
)
—128
(1
+
х)
(q>
u
—
Фз1
)
= 320У
10
;
—30(1—
v)(4q>
00
—5q>
20
)
—175(1—
5v/21)
ф
22
+
+
64
(1
+
2v/3)
(бфц-фя) +
31
Фзз
= 160V
12
,
где
Я Я/2
v
= — (3—a), V
kl
= — Г
cos /ip cos
o|?di|?
Г
VPik
(cos
ft)
sin
2
Mft\
Я/2 *0
a
—
скаляр, входящий в краевое условие (5.3.6),
—
переобозначен а.
При х = 0, V = 0 уравнения (6.3.21) превращаются в уравнения,
полученные В. С. Владимировым [41]. Вместо третьего уравнения в
(6.3.21) можно взять уравнение (6.3.15) при k = 1, / = 1:
-~(1-ха)ф
00
+^(^-у^ф
22
-
3/8 яи <-Л/ 1 \ 1
т/11
которое лучше выражает характер зависимости по ft и хуже — по
1]э.
Остальные три граничных условия определим при г = 0 следующим
образом:
Фп = Фз1 = Фзз = 0. (6.3.22)
Условия (6.3.22) являются следствием требования ограниченно
сти решения при г = 0. Получим соответствующие (5.3.6) граничные
условия на внешней границе круговой цилиндрической ячейки ге-
терогенного реактора при г = R.
Полагая в (6.3.21) к = 1, V = 0, получаем при г = R:
Фп = Фа = 0;
Фзз
= —~~ 0 —я)(4фоо — 5ф
20
) + ^ Ф22-
(6.3.23)
Если решение Р
3
-уравнений является самостоятельной задачей,
то можно находить а как результат минимизации М^-
0
'
r=R
§ 6.4. Pi-ПРИБЛИЖЕНИЕ. УРАВНЕНИЕ ДИФФУЗИИ
При решении многих задач, связанных с прохождением излучения
через вещество, зачастую бывает достаточно ограничиться Рх-прибли-
жением. В этом случае вектор-функции и матрицы, введенные в рас-
смотрение в предыдущих параграфах, будут иметь только по одной
компоненте.
107

} (6.4.2)
Ч
Ввиду того что нам потребуются уравнения (6.1.5) в Pi-приближе-
нии для любой геометрии, приведем отдельный вывод соответствую-
щей системы уравнений.
Рассмотрим кинетическое уравнение (5.1.4); решение его будем
искать в виде разложения (6.1.1) по сферическим функциям, ограничи-
ваясь лишь двумя членами разложения (при k = О, 1):
Ф
(х,
Й) = ф
0
(х) + ЗЙф
1
(х), (6.4.1)
где
Фх
=
Ф^
1}
i
+
Ф
(
1"
1}
j +
Ф1
к;
И
= sin
в
cos i|)i + sin9sini|)j + cos Эк.
Очевидно, имеют место соотношения
Фо(х) = (1/4я) JdQ9(x, Q); ф
х
(х) = (1/4я) fdQityfx, Q). (6.4.3)
Уравнение (5.1.4) проинтегрируем по Я. Тогда получим
?Ф
1
+ 2
0
ф
0
= /
0
, (6.4.4)
где
/
0
(х) = (1/4я)/ДУ (х, Q); 2
0
= 2-2
5
. (6.4.5)
Для получения второго уравнения подставим соотношения (6.4.1)
и (6.4.2) в уравнение (5.1.4), результат умножим на Q и проинтегри-
руем по всем телесным углам единичной сферы. Тогда будем иметь
(l/3)Vq>o + 2iih = fi, (6.4.6)
где
fi=(l/4«)JdQQ/(x,fl); S^S-S,^; Й>=у J g(x,h>)<K
Итак, получена система уравнений переноса излучения в Pi-при-
ближении для областей произвольной геометрии
Уф1
+ 2
0
фо-/о; О/З^Фо + ^ф^. (6.4.7)
Для одномерных плоской, сферической и цилиндрической геоме-
трий систему уравнений (6.4.7) можно упростить, если учесть симме-
трию.
Так, поместив начало системы координат в центр симметрии,
от векторной функции ф
х
можно перейти к скалярной фх на основе
равенства ф
х
= фх-п, где п — нормаль к поверхности Г. В этом слу-
чае система уравнений (6.4.7) приобретает вид
div (
ф1
п)
+ 2
0
ф
0
= /
0
;
(1
/3) grad„
Фо
+ 2
Х ф1
= f
v
(6.4.8)
Очевидно, что система уравнений (6.4.8) для плоскопараллельной,
сферической и одномерной цилиндрической геометрий совпадает с со-
ответствующими уравнениями, полученными из общих систем урав-
нений сферических гармоник (6.2.2), (6.2.18) и (6.3.10), (6.3.11) в Pi-
приближении.
108

Для полной определенности системы уравнений (6.4.7) к ней не-
обходимо присоединить граничные условия на поверхности Г. При
этом для простоты будем исходить из граничного условия (5.1.6). Для
получения приближенных граничных условий в соответствии с (6.1.7)
заменим (5.1.6) следующим:
fdQ|Qn|q>(x, О) =
0
на Г, (6.4.9)
где интегрирование ведется по единичной полусфере, образованной
концами вектора ft, направленными внутрь области D, и ограничен-
ной касательной плоскостью к выпуклой поверхности Г. Соотношение
(6.4.9) указывает на тот факт, что односторонний интегральный поток
нейтронов через поверхность Г со стороны вакуума в область D ра-
вен нулю.
Если предположить, что ось z совмещена с направлением внешней
нормали к поверхности Г в точке с радиус-вектором х, то условие
(6.4.9) запишется следующим образом:
2Я Я
f
dyp
f ф(х,
Q)
cos
О
sin МЪ = 0 на Г. (6.4.10)
0 Я/2
В соотношение (6.4.10) подставим функцию ф (х, ft), определенную
формулой (6.4.1), и проинтегрируем. В результате получим
2(ф1)
Л
-фо = ОнаГ, (6.4.11)
где (<Pi)n — проекция вектора ф
х
на внешнюю нормаль п к Г.
Для одномерных геометрий соотношение (6.4.11) приобретает
иростой вид
2
ф1
—
фо
= 0 на Г. (6.4.12)
Соотношения (6.4.11) и (6.4.12) будут требуемыми граничными
условиями для системы уравнений (6.4.7) на внешней границе.
Когда источники нейтронов изотропны, т. е. / (х, ft) = /
0
(
х
)> тогда
в Р
х
-приближении приходим к следующей системе уравнений:
Vф
1
+
2oФo
=
/o;
(l/3)V9o + 2i4)
1
= 0. (6.4.13)
Разрешив второе уравнение системы (6.4.13) относительно функции
ф
ъ
получим
ф1
=-£>Уф
0
, (6.4.14)
где D — коэффициент диффузии, равный D = l/(3Si). Подставляя
выражение (6.4.14) в первое из уравнений (6.4.13), приходим к урав-
нению диффузии
УЯУф
0
-2оФо = -/о. (6.4.15)
Граничные условия для функции ф
0
найдем с помощью соотно-
шения (6.4.11). Подставив в него ф
х
в виде (6.4.14), получим
2Я(Уф
0
)п + Фо = 0 на Г. (6.4.16)
109
