Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов

Подождите немного. Документ загружается.

Классическое решение задачи (6.4.15), (6.4.16) ищется в классе

функций {ф

}, непрерывных вместе с потоком ср

= — DV ф

и имею-

щих кусочно-гладкие производные от потока. Задачу (6.4.15), (6.4.16)

будем называть диффузионным приближением. Диффузионное при-

ближение совпадает с Pi-приближением при f

= 0. Если f

Ф 0,

то диффузионное приближение будет более грубым, чем Р

§ 6.5. МЕТОД ПОВЕРХНОСТНЫХ ПСЕВДОИСТОЧНИКОВ

В основе предложенного Н. И. Лалетиным [115] метода поверх-

ностных псевдоисточников лежит использование функции Грина для

получения решения в подобластях, из которых составлена вся об-

ласть D. Пусть область D составлена из подобластей D

(зон), внутри

которых коэффициенты уравнения (5.1.4) и индикатриса не зависят

от х; значения этих величин как постоянных, а также источник про-

должим на все пространство и снабдим индексом i. Границу области

обозначим S

. Решение в области D

будем искать в виде

*(х,

Q) = f jG,(x, Х', Й, 0')/,(Х', Q')dQ'dx' +

+ j j <jf'(x

Q')G,(x, x,'

Q')dQdS

(6.5.1)

h s

Здесь Gt (x, x', Q, Q') — функция Грина для однородной бесконеч-

ной среды, сконструированная по параметрам i-й зоны; x

£ S

, Q') — подлежащая определению функция, описывающая ин-

тенсивность поверхностных источников. Представление (6.5.1) удоб-

но для ряда задач ввиду существования достаточно простых аналити-

ческих выражений для угловых моментов функций б^.Для решения

неплоских задач функцию q

, Q) удобно задавать в виде

9Чг

в>

0)=-<7'(г., -О).

Поскольку решение исходной задачи ф (х, й) — непрерывная

функция вдоль каждой характеристики, то, приравнивая представле-

ние (6.5.1) на границах смежных зон и подставляя в граничные условия

представление (6.5.1), получаем систему интегральных уравнений для

определения функций q

, Q). Приближенный метод решения этой

системы, названный Ом-приближением, был предложен Н.И. Лалети-

ным

[115].

В нем функция Грина G

представляется в виде (5.6.9):

Gi =22^п(Й)П'(Й')0п^(х, х'), (6.5.2)

п п'

где Y

— сферические функции. Выражения для функций Грина для

одномерных геометрий приведены в гл. 5.

Использование выражения (6.5.2) после интегрирования уравне-

ний для ^(x

, Q) по направлениям приводит задачу к следующим

110

уравнениям (запишем их для частного случая двухзонной за-

дачи):

2Х(0)2

п п'

п'

f ^(x.)Gi

'(x

)dS

+QJ

= 2^п(«)Х

?S(x

)GJ^(x

)dS

+ Ql

(6.5.3)

где ^ (х

) = /?'(х

, Q') К* (Q') dQ'; Q£ — угловые моменты рас-

пределений нейтронов, создаваемых на границе зон объемными ис-

точниками ft (х, Я), а индекс суммирования п' пробегает лишь нечет-

ные значения в силу нечетности функций q

, Я). Из (6.5.3), при-

равнивая величины при Y

(Q), получаем бесконечную систему инте-

гральных уравнений для определения q

Для пространственно-одномерных задач (задачи с плоской, сфери-

ческой или цилиндрической симметрией) система (6.5.3) превращается

в бесконечную систему алгебраических уравнений. Полагая, что в раз-

ложении функции qt(Q) по сферическим гармоникам можно сохра-

нить лишь моменты с номерами п' ^ N (GN-приближение), оставляем

из этой системы лишь необходимое количество уравнений с малыми п,

В простейшем случае достаточно взять уравнения cn<iV. Отметим,

что в любом Gjv-приближении получается решение, точно удовлет-

воряющее кинетическому уравнению внутри зон. Ошибки метода воз-

никают от приближенного выполнения условий сшивки решения на

границах зон. В такой трактовке этот метод родствен методу Треффца

[25].

В работе Н. И. Лалетина и И. В. Султанова (см. в [116]) показа-

но,

что предпочтительнее получить уравнения типа (6.5.3) из требова-

ния непрерывности моментов функции (Q, п) ф (х, Q). Этот метод

можно трактовать и как вариационный, если уравнения для определе-

ния моментов

получать как уравнения Эйлера в задаче миними.

зации квадратичного с весом функционала, определенного на грани-

це зоны:

(Ф1.

Ф2> Р

(х

, О)) = j J

(Ф1—ф

)

(х

О)

dQ.

В частности, за вес р целесообразно взять функцию | (Q, п) |.

§ 6.6. РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА МЕТОДОМ СФЕРИЧЕСКИХ

ГАРМОНИК ПРИМЕНИТЕЛЬНО К КВАДРАТНОЙ И ШЕСТИУГОЛЬНОЙ

ЯЧЕЙКАМ ГЕТЕРОГЕННОГО РЕАКТОРА

Излагаемый ниже прием расчета ячеек квадратной и шестиуголь-

ной формы в рамках метода сферических гармоник был в диффузион-

ном приближении впервые опубликован В. П. Кочергиным и Г. И. Мар-

чуком [166] и распространен позднее В. В. Смеловым и Г. А. Илясо-

вой на случай Р

-приближения

[214].

В окончательном виде метод

излагается в формулировке В. В. Смелова.

Ill

Постановка задачи

В односкоростном приближении поток нейтронов в бесконечной по

высоте цилиндрической ячейке описывается уравнением:

VTr^cos^ +

i^i-^j

+ ^r, G)-

's,g(r,a'^a)q.(r,Q')<(a'=nr, а), (6.6.1)

где г = (г, со); Й = (г|), G); у = cos 0.

Ввиду симметрии ячеек относительно линий ОМ и ON (рис. 6.1)

достаточно найти решение уравнения (6.6.1) в области OMN; при

этом угол со меняется в пределах 0 ^

со

^ /, где / = я/4 для

квадратной ячейки и / = л/6

для шестиугольной.

Из симметрии ячейки, а так-

же из бесконечной протяжен-

Jj ности ее вдоль оси z следует, что

Ф^, со,г|),

y) =

q>{r,

со

2/, *ф,

Т)

ф(Л— со,

—

г|),

у) =

Ф(г, со,

-ф,

—

Y)-

(6.6.2)

Рис. 6.1. Модели двумерных ячеек

Для решения задачи методом сферических гармоник базисную си-

стему сферических функций можно сформировать с использованием

присоединенных функций Лежандра

P«

(Y)-

Пусть

9>w

{y)==i

(у)/(п

т)\

^(m)^

= g&(-m)(

)

;

^(m)(

)-o при п<0; &w

(у)

при \т\>п.

Рассмотрим теперь следующие функции:

Sfti

(<°.

*•

т)

(Т) exp [i

(т * +

со)], A

= jiv//

= 0, 1, 2, ...; т = 0, ± 1, ±2, ..., ± п\ v = 0, ± 1, ±2, ...

Нетрудно убедиться, что S

{

nm (со, г|), у)

—

собственные функции

уравнения

п 2Ч

6S , 1 ass , ^2S

—

(1—

у)—\

ду

v r ;

i—7

df*

f^. +

отвечающие собственным значениям и = п (п + 1) +

Я*.

Эти функ-

ции ортогональны в области — /^co^Z; 0^о|)^2я; —

<1у^ 1;

/ 2Л 1

jdco jd^j dyS^(^^y)S^{co

%y)==

8я/

—1

' (2п+\)(п + т)\(п—

т)\

при п

= я

» Щ

т\ v

= v

;

в остальных случаях.

112

Приближенное решение

Ф(/\^СО,

ф, у)

уравнения (6.6.1) будем

ис-

кать

виде

2N+1 п 8

Ч{г,<о,Ы)=± ^ 2 2 (2«+l)(n +

m)!(n-m)!

xCW(r)S(v

)

(

co^,

), (6.6.3)

где

/ 2Л 1

^(0 = ~- jdcofdt|) |ауф(Лсо,г|),

)5^((о,ф,

Представление (6.6.3) обеспечивает выполнение первого

из

условий

(6.6.2),

остальные из этих условий (с учетом вещественности искомой

функции

ф)

приводят

тождествам:

qv> (г)

СМ (г).

lyn q

(г);

СМ (г)_

при

т нечетном.

(6.6.4)

Тождества (6.6.4) позволяют сократить число дифференциальных урав-

нений, связывающих функции

Спт

{г)- Отметим,

что

функции Спт

вещественны.

Подставив разложение (6.6.3)

уравнение (6.6.1), проинтегрируем

его по всем переменным у, г|>, со

весом S

(со,

if, у). В

итоге неслож-

ных преобразований [213] для каждого

из

значений

v =

О,

1,2, ..., s

получим систему обыкновенных дифференциальных уравнений отно-

сительно фуНКЦИЙ Спт

(&-

(«

+ m +

l)(» + m+2)[i%^+^

[

7 4-l.m+lJ-

(

„_

m+1)(n

m+2)

[<^_(^zbLqv

, ^]

-2(2n-f-l)(

„C^_Q(v^

0, (6.6.5)

где

— коэффициенты Фурье функции источников;

= 2 - 2 я

(л!)

f g

(r,

-*Q)^

(fi

)

d|A

h» = "

; * =

0, 1, ..., 2 N + 1; m = 0, ±1, ..., ±я. В

силу (6.6.4) достаточно

считать, что

v = 0, 1, ..., 5, а

параметр

при заданном значении

пробегает

тот

набор

из

чисел

0, ±1, ..., ±я,

когда

п + т

— четное

число.

113

Систему (6.6.5) дополним граничными условиями.

Центр ячейки.

При г =

функции

С^

подчиним следующим тре-

бованиям:

Ж(0)

Кфт\

dC?J

r=0

0 при

|A,

— т\ф!

(

)

= nv/l

— целочисленный параметр.

Граница

зон

ячейки. Потребуем непрерывности потока нейтронов

йпф

(/?,

со; г|),

у)

через границу раздела двух сред

г = R. Из

непрерыв-

ности

его и на

основе разло-

/V жения (6.6.3) устанавливаем

\^u?/Q^np(r,(j)Q непрерывность следующих

ком-

бинаций:

(п+т+1) (д+т+2)

СЭД

w+1

— (я —т + l)(/i—т +

х^,,

■C<

(6.6.7)

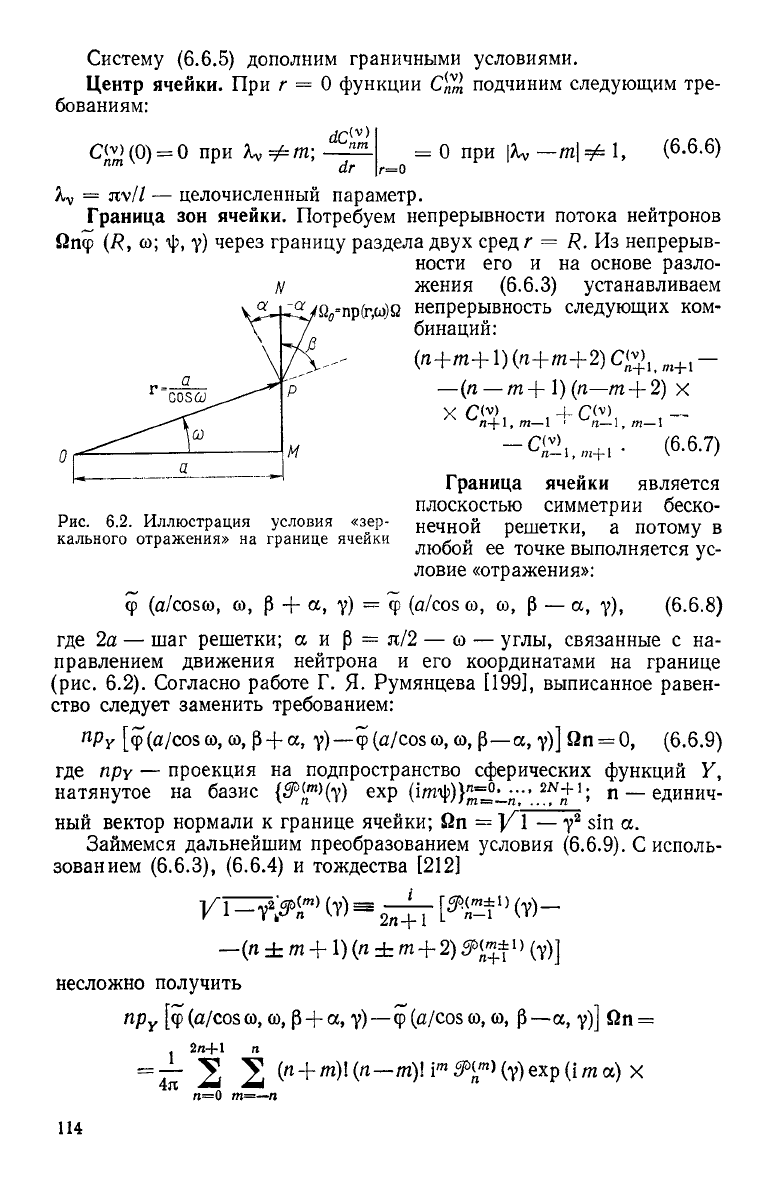
Рис. 6.2. Иллюстрация условия «зер-

кального отражения» на границе ячейки

Граница ячейки является

плоскостью симметрии беско-

нечной решетки,

потому

любой

ее

точке выполняется ус-

ловие «отражения»:

Ф (a/cosco,

со, р + а, у) =

ср (а/cos

со,

со, р

—

а, у),

(6.6.8)

где

2а

— шаг решетки;

а и р = я/2

— со — углы, связанные

с на-

правлением движения нейтрона

и его

координатами

на

границе

(рис.

6.2).

Согласно работе

Г. Я.

Румянцева

[199],

выписанное равен-

ство следует заменить требованием:

Ру

[Ф

(a/cos

со, со,

+а, 7)—Ф (a/cos

со, со,

р—а, у)] йп

0, (6.6.9)

где

пру —

проекция

на

подпространство сферических функций

натянутое

на

базис

{№

{

™Цу)

exp

(imi|?)}^^"

;

— единич-

ный вектор нормали

границе ячейки;

йп = Y\ —у

sin a.

Займемся дальнейшим преобразованием условия (6.6.9). С исполь-

зованием (6.6.3), (6.6.4)

тождества

[212]

УГЧ'У

т)

(V)

- ^ [9£Lt> (V)-

—(п±т + 1){п±т + 2)&^)(у)]

несложно получить

[ф(a/cosсо,

со,

сх,

у)—<р(a/cosсо,

Р—а, у)]

ftn =

2/i-H п

= 7" j 2 (» + «)>(«—«Mi"^"

(Y)exp(ima) X

4JC ^~ ^**

п=0 m=—n

114

v=—s

-<-

ЫЫ

cos

[-7+(

)

]}

•

10)

где

l^) =

+ m+l){n +

+ 2)C^

Um+2

(r)-C^

m+l

(ry,

r\M(r)

= {n-m+l){n-m + 2)C^

(r)-C£>

lt m

(r).

Общее решение системы обыкновенных дифференциальных урав-

нений (6.6.5) содержит конечное число свободных параметров, ни

одной из комбинаций которых невозможно удовлетворить требованию

(6.6.9) тождественно во всех точках MN границы ячейки (см. рис. 6.2).

Таким образом, условию (6.6.9) можно удовлетворить лишь при-

ближенно. В предлагаемом алгоритме выбор свободных параметров

будет основан на минимизации нормы невязки граничного условия

в метрике L

J dL fdQ {[ф (Р, р + а, у) -

(Р, р - а,

у)]

Qn}

= min (6.6.11)

(где dL

—

элемент длины вдоль границы MN, dQ =

dyda)

при усло-

вии выполнения баланса по всей длине MN:

{dL 2

C[V

Wco8(iv-1)(D==0, (6.6.12)

MN V—в

Pi-приближение

Полагая в разложении (6.6.3) N= 0, приходим к Р

приближению

Система уравнений (6.6.5) примет вид*

•

rfr r

1,-1

00 / v0>

{v)

dtf

(6.6.13)

Исключая в полученной системе С

(

п и C^Li, получаем уравнение

диффузионного типа относительно функции

Соо:

1 d г dCffl , ( \ Ч

г dr 32

(-^4

+20

)

С<Л)==/б

(

6Л4

* Система (6.6.13) записана в предположении, что функция источников /

изотропна и не зависит от пространственных координат в каждой из зон ячейки.

Это предположение будет использовано и ниже в Р

-приближении.

115

В Рх-приближении запишем теперь краевые условия и условия сшив-

ки.

В центре ячейки из (6.6.6) находим

= 0.

(6.6.15)

dr |г=о

На границах зон из (6.6.7) устанавливаем непрерывность величин

ОД и —

№

dr '

(6.6.16)

На границе ячейки соотношения (6.6.11) и (6.6.12) с использованием

формулы (6.6.10), а также с учетом связи элемента длины с элемен-

том угла (dL = adco/cos

(o) превращаются в следующее требование:

еде

cos (h

-l)coJ

d(D

= min

COS

при условии

Л I dC(y)

^С!

I / 00

ddd

COS

C[V(r)\

cos(Xv

—

l)co x

(6.6 Л 7)

Для решения задачи (6.6.14)—(6.6.17) ячейку удобно дополнить

до круговой, внешняя граница которой представляет собой описан-

ную около реальной ячейки окружность. Обозначим #

эф

= a/cos/

радиус этой окружности. Метод решения состоит из следующих двух

этапов.

Получение «общего» решения* (6.6.14) при каждом значении

v = 0, 1, 2, ..., s; оно может быть записано в виде

qV(r) = x(v)

(v)(

)

o(r),v = 0, l,...,s.

(6.6.18)

Здесь ф

(г) — частное решение неоднородного уравнения (6.6.14)

при v = 0, удовлетворяющее в центре ячейки и на границах зон ус-

ловиям (6.6.15) и (6.6.16); cp

(v)

(г) — решение однородного уравнения,

соответствующего уравнению (6.6.14), которое удовлетворяет ус-

ловиям (6.6.15) и (6.6.16), а при г = Я

эф

— условию (p(

> (#

эф

) = 1.

* Здесь под общим решением понимается то многообразие решений, зави-

сящее от одного произвольного параметра, из которого может быть получено

любое частное решение, удовлетворяющее условиям (6.6.15), (6.6.16).

Численные методы расчета функций ср

(г), cp

(v)

(г)

хорошо извест-

ны

[162].

Определение констант x<

общих решениях (6.6.18) на основе

требований (6.6.17). Подставляя (6.6.18)

(6.6.17), приходим

к си-

стеме алгебраических уравнений относительно коэффициентов x<

Рз-приближение

Рассмотрим более высокое Р

-приближение, когда

(6.6.3)

N = 1.

Поскольку вся идейная сторона метода изложена

п. 2, здесь приве-

дены только основные результаты без дополнительных разъяснений.

В Рд-приближении система (6.6.5) состоит

из

десяти уравнений

для

каждого

Если ввести векторные функции

o<v)

[(i/2)

cft

qv)_

, qv>, бед;

(

qv)_

CJ;L,.

cft>,

ОД].

то упомянутая система может быть переписана в виде

*^L

± p(v)

i(v)

0<v)

= s

;

d^ J__

r( )ф(л;) r I(v)==0

dr r

2 3

где

P и Г

— матрицы;

— вектор источников.

В выписанной системе

—

диагональная невырожденная мат-

рица,

что

позволяет легко исключить

из

этой системы вектор

(v)

В итоге

каждой из зон ячейки, где физические параметры считаются

постоянными, получаем систему дифференциальных уравнений вто-

рого порядка:

dr»

г dr [^ г* )

= -32

S6vo,v = 0,l,...,s, (6.6.19)

где 2 = diag

ВД,52л2

,52

, 5ВД];

—(3

+ 2X

)g 2d

О (l-2Xv)Sf

117

2AV

—A (2-|-Ay ) —2Av Ay (2 —

Av)

Л = | —M2 + M

+ K)

h K(2 + K)g 0

—

2K K(2 + K)g 2%%d —l

(2 — K)g

(2—K)

0 —K(2—K)g (2—K)

В работе [213] показано, что при г = 0 условия (6.6.6) эквивалент-

ны таким:

dO>(v)/d/1

o-0,v = 0, l,...,s. (6.6.20)

На концентрических границах R раздела зон из (6.6.8) вытекают

условия

>(#—0) = <D<v>(i?-f 0);

(6.6.21)

где JV

(V)

и Л4 — матрицы четвертого порядка, получение которых не

представляет трудностей.

На границе ячейки условие (6.6.11) принимает вид

/2=0 m=—n lv=—s

+ (^-(т+1))со]-Л^

J J

i (6.6.22)

при условии (6.6.12).

Дополняя теперь реальную ячейку до круговой, решим задачу

в два этапа: найдем все линейно-независимые решения задачи (6.6.19)—

(6.6.21),

а постоянные определим из (6.6.22) и (6.6.12).

§ 6.7. РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА МЕТОДОМ СФЕРИЧЕСКИХ

ГАРМОНИК ПРИМЕНИТЕЛЬНО К ЯЧЕЙКАМ СО СЛОЖНОЙ

ГЕОМЕТРИЕЙ

Ячейки гетерогенных реакторов имеют часто более сложную

структуру, чем это описано в § 6.6. Так, минимальный элемент се-

чения ячейки, несущий всю информацию о ней, может иметь, например,

вид, изображенный на рис. 6.3 (в дальнейшем элементы ячеек, пред-

ставленные на рис. 6.3, будем называть просто ячейкой).

Излагаемый метод, разработанный В. В. Смеловым, является

продолжением материала § 6.6, а потому в нем будут использованы

полученные выше результаты. Основную идею метода разберем на

примере Р

-приближения.

118

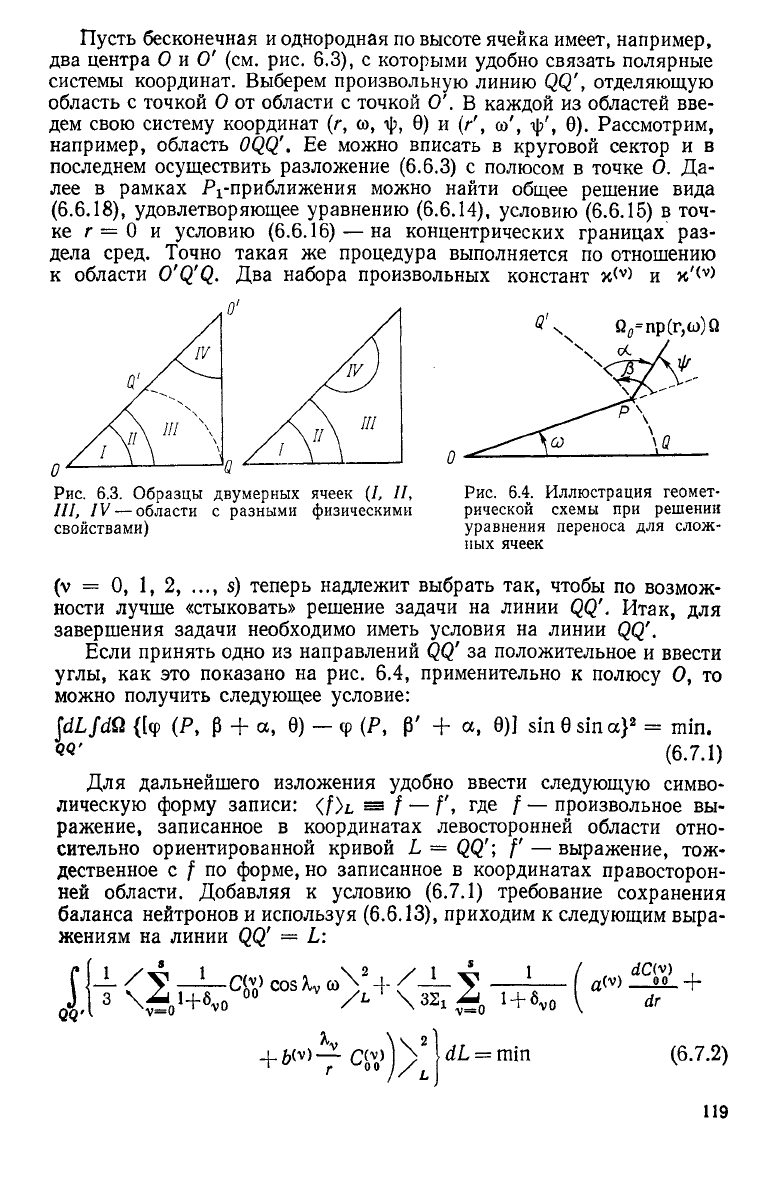
Пусть бесконечная и однородная по высоте ячейка имеет, например,

два центра О и О' (см. рис. 6.3), с которыми удобно связать полярные

системы координат. Выберем произвольную линию QQ', отделяющую

область с точкой О от области с точкой О'. В каждой из областей вве-

дем свою систему координат (г, (о, -ф, 9) и (г', со', я|/, 0). Рассмотрим,

например, область 0QQ'. Ее можно вписать в круговой сектор и в

последнем осуществить разложение (6.6.3) с полюсом в точке О. Да-

лее в рамках Р

приближения можно найти общее решение вида

(6.6.18),

удовлетворяющее уравнению (6.6.14), условию (6.6.15) в точ-

ке г = 0 и условию (6.6.16) — на концентрических границах раз-

дела сред. Точно такая же процедура выполняется по отношению

к области

O'Q'Q.

Два набора произвольных констант x<

> и x'<

Рис.

6.3. Образцы двумерных ячеек (/, //,

///, IV — области с разными физическими

свойствами)

Рис.

6.4. Иллюстрация геомет-

рической схемы при решении

уравнения переноса для слож-

ных ячеек

(v = 0, 1, 2, ..., s) теперь надлежит выбрать так, чтобы по возмож-

ности лучше «стыковать» решение задачи на линии QQ'. Итак, для

завершения задачи необходимо иметь условия на линии QQ'.

Если принять одно из направлений QQ' за положительное и ввести

углы, как это показано на рис. 6.4, применительно к полюсу О, то

можно получить следующее условие:

JdL/dQ {[ф (Р, р + а, 6) —

<р

(Р, Р' + а, 0)] sin 6 sin а}

= min.

W (6.7.1)

Для дальнейшего изложения удобно ввести следующую симво-

лическую форму записи: </>£, нз / — /', где / — произвольное вы-

ражение, записанное в координатах левосторонней области отно-

сительно ориентированной кривой L = QQ'; /' — выражение, тож-

дественное с f по форме, но записанное в координатах правосторон-

ней области. Добавляя к условию (6.7.1) требование сохранения

баланса нейтронов и используя (6.6.13), приходим к следующим выра-

жениям на линии QQ' = L:

i з V

.ЧАо

CJS>cos*

©Y

+ /

'00

\32i

v=0

'v0

a(v) oo_

wv>7>

CR))^]

dLs=min

)

119