Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов

Подождите немного. Документ загружается.

0 , А=1; |

^=iis.

-L-

ip/ii6*-

-e*.i

. л—ж.

2....J

(11.24.12)

Реализация этих формул уже не вызывает никаких затруднений и

требует дополнительно к О (Nm) арифметических действий, необхо-

димых для вычисления вектора SL~

по заданному вектору

gfe-i £ и

Ау

только О (N) арифметических действий. При этом объем

памяти ЭВМ, достаточный для реализации процесса, составляет

О (N) ячеек.

В общем случае трудности, вызванные участием в скалярных

произведениях, легко устранимы путем изменения вычислительной

схемы и использованием второго из соотношений (11.24.11). Окон-

чательные трехчленные формулы этого процесса имеют вид:

ао

= 1-

(5ф+/); Й°=1-

ИФ-Л;

S°

;

]

qh=gk-i—(Vgk) [(/—L^S) ft-i—«fc-itefc-i—ft-i)l;

10 , , k=U

(

((/-SL-i)6*-S gk-W-SL-*)l

~\g

h+2

\ k > 1;

^ = ((/-SL-*)6*-»

(/-L-^ft-iVaZ-SL-i)?*-»,^!)-

(11.24.13)

§ 11.25. МЕТОД РАСЩЕПЛЕНИЯ ДЛЯ РЕШЕНИЯ СИСТЕМЫ

СФЕРИЧЕСКИХ ГАРМОНИК

Метод сферических гармоник позволяет сформулировать краевую

задачу для системы дифференциальных уравнений относительно ко-

эффициентов в разложении искомой функции по сферическим гармо-

никам. В многомерном случае даже при низких порядках приближе-

ний матричная факторизация оказывается затруднительной из-за не-

обходимости обращения матриц высокого порядка.

Для многомерных уравнений метод сферических гармоник мог бы

удачно дополниться методом расщепления. Система уравнений сфери-

ческих гармоник в Pjv-приближении представима в виде (R + Z +

+ £) ф = /, где R — матрица с элементами, зависящими только от

r\ Z — матрица с постоянными коэффициентами; 2 — диагональная

матрица, элементы которой зависят от г и от г. Матрица R обладает

410

Тем свойством, ^то бна йвнб распаДаетРсй на Две квадратные подма-

трицы, одна из которых (R

) действует на компоненты вектора ф,

имеющие четную сумму верхнего и нижнего индексов (ф„), а другая

(/?

) действует на компоненты вектора ф с нечетной суммой индек-

сов,

т. е.

«,_Ш4-"|[Ч

°IRKJL<P»J

Матрица Z после соответствующего упорядочения компонент векто-

ра ф также представима в блочно-диагональном виде:

2ф

N-\

0 =

Г гпО"~|

где z

— квадратная матрица размерности N — т + 1; N — поря-

док приближения (PN). Следовательно, на диагонали матрицы Z

расположены квадратные блоки убывающей размерности и система

2ф =

распадается на N + 1 подсистему уравнений, не связанных

между собой. Здесь ф

—вектор с компонентами, верхний индекс ко-

торых равен т. Система краевых условий в форме (6.3.15) расщепля-

ется следующим образом. На боковой поверхности цилиндра эти ус-

ловия разбиваются на две независимые подсистемы: Л

(R, г) =

= 0, Л

(R>

z) = 0. Это позволяет при использовании метода

расщепления полностью разделить решение систем с четной и не-

четной суммой индексов при неизвестных моментах на две не за-

висящие друг от друга задачи. На торцах цилиндра система граничных

условий также разбивается на независимые подсистемы £

= 0;

т= 0, 1, ..., N— 1. Ради простоты эту методику проиллюстрируем

на примере стационарного односкоростного уравнения переноса в

Pi-приближении для конечного цилиндра без азимутальной зависи-

мости. В этом случае система уравнений сферических гармоник при-

нимает вид:

1 д

, д

— —

^Ф1

+ —

г дг дг

*» + 32,Ф1=ЗЯ;

дг

(11.25.1)

411

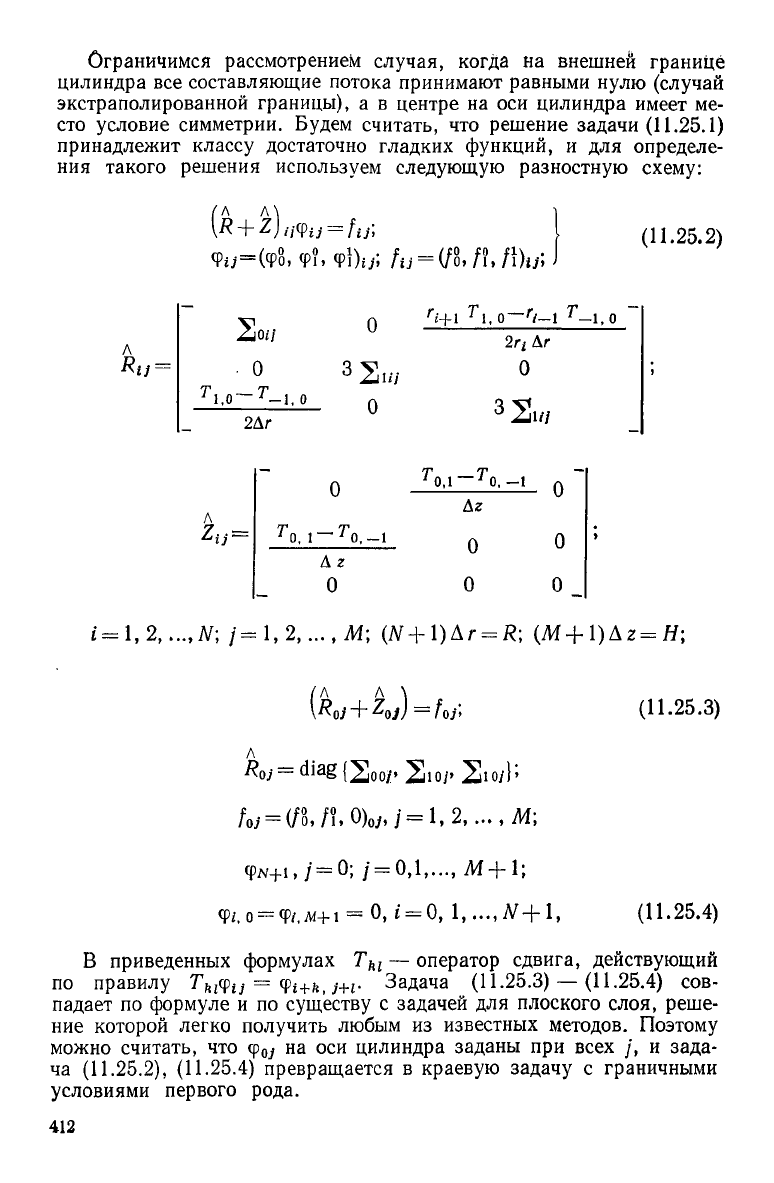
Ограничимся рассмотрением случая, когда на внешней границе

цилиндра все составляющие потока принимают равными нулю (случай

экстраполированной границы), а в центре на оси цилиндра имеет ме-

сто условие симметрии. Будем считать, что решение задачи (11.25.1)

принадлежит классу достаточно гладких функций, и для определе-

ния такого решения используем следующую разностную схему:

(А Л\

(11.25.2)

1,0~~^—1.

2Дг

2.1/

i+i

1.0"

/-1

-1, о

1//

Тр,

—

^о, —1

Дг

^o.i

—^о,

—1

0 о

*=1,

2, ...,#; /=1,2,..., М\ (N+l)kr =

+ l)Az = H;

/л л \

\#0/

oj) =

/о/»

(11.25.3)

0jf

—diag{2oo/» Si

о/»

2ю/}»

/o;

= (/°oJbOU/=l,2,...,M;

Ф*+1,/

/ =

0,1,...,

M+\\

Фло =

Флл!+1

= 0, i = 0,

1,...,#+!,

(11.25.4)

В приведенных формулах T

— оператор сдвига, действующий

по правилу

к1

i+k

ж- Задача (11.25.3) — (11.25.4) сов-

падает по формуле и по существу с задачей для плоского слоя, реше-

ние которой легко получить любым из известных методов. Поэтому

можно считать, что ф

^ на оси цилиндра заданы при всех /, и зада-

ча (11.25.2), (11.25.4) превращается в краевую задачу с граничными

условиями первого рода.

412

Для решения указанной задачи можно применить следующий ите-

рационный алгоритм:

/=1,2,...,#; /=1,2,...,М;

Ф&+1,/

= Фо/ =

°;/^

1. А1+1;

(11.25.5)

Здесь т > 0 — параметр, который можно выбирать на основе

метода минимальных невязок (см.§ 29, гл. 10). Граничные условия на

оси цилиндра учтены в f

. Следуя работе Ю. Е. Бояринцева и

О. П. Узнадзе*, введем в рассмотрение пространство и векторов

размерности N X М:

= (фн> Ф12> •••• ф1ЛЬ Ф21> Ф22> •••! ф2ЛЬ ••., фЛП , фЛГ2, • •, флш),

где,

в свою очередь, ф^ — трехкомпонентные векторы, обращаю-

щиеся в нуль на границе рассматриваемой области. Определим далее

в этом пространстве скалярное произведение [,] и норму следующим

образом:

М N

[a,v]=2 2 riivu^ii)* teA\u\\ = V[u*u\- (И-25.6)

/=i /=i

Здесь (ф^-, tytj) — евклидово скалярное произведение. В качестве

нормы оператора, действующего во введенном пространстве, будем

брать норму, подчиненную норме векторов (11.25.6).

Для доказательства сходимости итерационного метода (11.25.5)

достаточно показать, что все собственные числа оператора шага этого

процесса С = (I + rZ)"

(I + т$)~

(1 — tR) (I — TZ) ПО модулю

меньше единицы. Здесь R и Z — матрицы с элементами Rtj и Z^-.

Очевидно, что множества собственных чисел оператора С и подобного

ему оператора С = (/ + xZ) С (I +

TZ)"

совпадают. С другой сто-

роны, собственные числа оператора не превосходят его нормы. По-

этому достаточно будет доказать, что

|с|к1(/+^Г('-тк)||11(/+гГ

(/-^)|<1. (.1.25.7,

Покажем, что

I(/

+ Tz)~'(/-Tz)||=l,a||(/-bT^)(/-T^)||<l.

* Бояринцев Ю. Е., Узнадзе О. П. Об одном способе решения нестационар-

ного уравнения переноса. — ДВМ и МФ, 1967, т. 7, № б, с. 1406.

413

Действительно,

I + xz)

{l-xz)f

Аналогично

=sup [(

+^)

[l-rz)u

(l+xb)

(l^z)u]

IIMII

¥=0

|(/— %z\u

(/—TZJUI

SUp ^ - i-J- =

»*°{(l

rz)u,(l+rz)u\

sup

t«. »1"^.

»1+f

[а>Л]

(11

25<8)

,ШФ

° [и,

+ 2x[zu, «J+та [zu, Zu]

;+т

Г (/-*)!'-

sup ^ «!-*№«. «)+*№*. *«1 . (Ц.25.9)

ll«ll£o [a,

+ 2t[#w,

II]+*[/?«.

#и]

Используя определение скалярного произведения и равенство

нулю векторов ср^ на границе области, имеем

ГЛ 1 Л* N /

izii, «J =

Ф*/>

ФШ

Ar А2==

/=1 /=1

N j М

= 2 Г|Аг 2 [Го.1-Го.-1]Ф?// Фо// —

-2 (7*о.

i —

То.-0

Ф?#/Ф.8//^

(11.25.10)

/-1 /

ГЛ I М N /д \

[ЛИ,

И]

= 2 2

* 1

?иФи,Ф|^АгДг =

==2 2

*('2о//К/)

+з^

——

I \

i Ф1//Ф0// +

'°

2Ar

1,0

Фо//

ФЬ/)

2Дг

I g

(So./ Л)

+3 2u/ (Ф?//)

2w/

(Ф!//)

)

°-

(11.25.11)

Соотношения (11.25.8)—(11.25.11) доказывают неравенство

(11.25.7). Вопросы численной реализации этой схемы также освеще-

ны в работе Ю. Е. Бояринцева и О. П. Узнадзе. Этот метод распро-

страняется на случай Р^-уравнений метода сферических гармоник.

414

§ 11.26. ФАКТОРИЗОВАННЫЕ ОПЕРАЦИИ

Поскольку главную трудность для многомерных задач составляет

в операции

обращение операторов

R =

Q —

Рс>

интересно рас-

смотреть такие операторы/?, которые представимы

виде произведе-

ния одномерных дифференциальных операторов. Тогда трудность на-

хождения R~

заметно снизится. Операторы

R в

операции

приме-

няют для вычисления ошибки. Идею построения факторизованных

уравнений изложим на примере периодической задачи, когда решение

ее не зависит от л;

. Положим оператор

= /, а

операторы

R и Р

ищем

виде

(1_

)-1/2/« J^

(!_

)I/2

= !—b

k +

аЧ*

dxf

(1-е)

дх\ Ьх\

(11.26.1)

где

а,

&!, Ь

— неизвестные параметры. Можно убедиться, что при

таких операторах

R, Р

/(Рх-метод будет балансным,

спектральная

функция перехода для пробной функции вида exp [i (п

)]

имеет вид сф, где

♦('. 9)

= r(Q-[l-*4fl]

^а^ +

аЧ^т

2ф/[4(1^)]

т/ w w

-с

af*

d»/«

sin2 2ф

/[4

—с)]

(11.26.2)

а ф •-- arctg (n

//ii). Из вида функции а|э (/, ф) следует, что

max |i|)|

max (max |г|) (/, 0)|, max |\|? (/, я/4)|).

t t

Варьируя всю группу неизвестных параметров

или толь-

ко некоторые из них, находим т

= min max

|г|э|,

где O^d^

t <p,0<c<rf

Результаты расчета для некоторых значений с, близких

единице,

приведены

табл. 11.4.

ней варианты со значениями bt

= 0

соот-

ветствуют априорным предположениям относительно этих неизвестных.

Таблица 11.4

0,9

0,201 0,24

0,24

0,9

0,287

0,253 0,254

0,9 0,165 0

0,33

0,99 0,197

0,488 0,488

0,489

0,99 0,191 0

0,493 0,495

0,999

0,187 0,72 0,72 0,75

0,999

0,173 0

0,805

415

Если учесть, что скорость сходимости простой итерации оцени-

вается величиной —lnc, а скорость сходимости в излагаемом методе

есть — (In с + In m), то при применении факторизованных уравнений

получим ускорение сходимости в 1 + In m/ln с раза.

Дифференциальные операторы предложенного типа можно при-

менять и при решении основной краевой задачи для двумерной области,

составленной из прямоугольников со сторонами, параллельными осям

координат. От функции оУН-1/2 нужно тогда потребовать, чтобы она

удовлетворяла на границе области однородным условиям типа Мар-

шака—Владимирова. Метод решения разностных уравнений с рас-

щепляющим оператором изложен в работе [80].

Основываясь на результатах §11.12, можно утверждать, что

больший эффект ускорения сходимости итераций будет иметь место

при применении факторизованных уравнений в /(^-методе. В этом

случае вид операторов R, Р и спектральной функции в /(^отличает-

ся от вида операторов /?, Р и спектральной функцииг|;в КР (1), выра-

женных формулами (11.26.1), (11.26.2), только тем, что вместо вели-

чин с и r(t) в этих формулах стоят величины с

и г

(/). В табл. 11.5

приведены результаты расчетов оптимальных значений a, b

ля

Рг

(1).

Таблица 11.5

Ьх

Ьг

0,9

0,443

0,184

0,99 0,4 0 0 0,455

0,999 0,362 0 0 0,733

0,9 0,478 0 0,144 0,144

0,99 0,425 0 0,37 0,37

В рассмотренных методах АЦ = О (Л/).

Приложение 1

ПРОГРАММЫ

На протяжении ряда лет сотрудниками Института атомной энергии им*

И. В. Курчатова и Вычислительного центра СО АН СССР были созданы програм-

мы решения уравнения переноса нейтронов в различных приближениях и для

разных геометрий. В основу алгоритмов положены аппроксимации уравнения,

изложенные в гл. 6—9, и итерационные методы, описанные в гл. 10, 11. Про-

граммы оформлены в виде'препринтов, в которых содержатся подробные описа-

ния программ и перечисляются их особенности. Авторы в настоящем изложении

не ставят своей целью сделать обзор всего программного хозяйства, созданного

в Советском Союзе для решения реакторных задач. Однако среди других про-

грамм упомянем, систему «Радуга» [19], состоящую из библиотеки модулей для

решения уравнения переноса в средах с осевой симметрией.

416

§ П1.1. СЕТОЧНЫЕ ОДНОМЕРНЫЕ ПРОГРАММЫ

Плоская геометрия. Для этого случая Ю. А. Власовым составлены следую-

щие программы.

Решение одногруппового кинетического уравнения в Pi-приближении

для плоской геометрии. Препринт ИАЭ-2407, М., 1974.

Решение кинетического уравнения в Р

-приближении в плоской геомет-

рии. Препринт ИАЭ-2513, М., 1975.

Решение уравнения переноса нейтронов в плоском слое. Препринт ИАЭ-

2588,

М., 1975.

Решение кинетического многогруппового уравнения в Р

-приближении

для плоской геометрии. Препринт ИАЭ-2514, М., 1975.

Решение многогруппового уравнения переноса нейтронов в плоском слое.

Препринт ИАЭ-2562, М., 1975.

6. Программа численного решения уравнения Больцмана для плоской гео-

метрии. Препринт ИАЭ-2958, М., 1978.

Программы 1—3 находят решение методом сеток одногрупповых уравнений

^i"» -Рз-приближения и одногруппового уравнения переноса. Для уравнений

сферических гармоник использованы разностные схемы повышенной точности и

метод матричной факторизации, описанные в § 7. 4—7. 6. Решение уравне-

ния переноса находится методом характеристик с применением формул, описан-

ных в § 9.9. Для ускорения итераций применен циклический /(Р1(2)-метод, ис-

пользующий уравнения типа Р

ближения для поправки (см. § 11.16).

Индикатриса рассеяния и источник уравнения могут быть линейно-анизотроп-

ными. Краевые условия могут быть либо условиями зеркального отражения, либо

условиями Маршака — Владимирова (см. § 6.2). Для уравнения переноса можно

задавать и периодические условия.

Программы 4—6 позволяют численно решать многогрупповые уравнения.

Значения потока и тока нейтронов в каждой группе вычисляются в узлах сетки,

которая строится в каждой зоне самой программой так, что она сгущается у гра-

ниц зон (см. § 9.9). Программы позволяют решать как задачу с заданными источ-

никами, распределенными по границам и зонам, так и задачу на собственное зна-

чение (/г

ф) (см. § 1.3). Во втором случае вычисляется кроме потоков и токов про-

странственное распределение функции мощности генерации вторичных нейтро-

нов.

Эффективный коэффициент размножения я

ф вычисляется методом простой

итерации в программах 4,5 и чебышевским методом с применением Г-последова-

тельности и определением двух максимальных собственных чисел (см. § 10.32).

В программах 5,6 в качестве начального приближения к решению многогруп-

пового уравнения переноса берется решение соответствующих Р

-уравнений,

т. е. все выходные величины сначала вычисляются в Р

-приближении, а затем

в кинетическом приближении.

Цилиндрическая геометрия.

Для этого случая С. И. Коняевым составлены такие программы.

Решение кинетического уравнения в цилиндрической геометрии в Р

приближении. Препринт ИАЭ-2395, М., 1974.

8. Решение многоскоростного кинетического уравнения в Р

-приближении

в цилиндрической геометрии, Препринт ИАЭ-2396, М., 1974.

С. А. Фроловой составлена программа РЕКИНУР:

9. Программа решения многогруппового кинетического уравнения в цилинд-

рической геометрии. Препринт ИАЭ-2481, М., 1975.

По программам 7,8 вычисляются решения соответственно одногруппового и

многогруппового уравнений в Р

-приближении. Разностная аппроксимация

-уравнений в одной группе производится по формулам § 7.3; для решения

применен метод матричной факторизации (см. § 7.6). Программы позволяют нахо-

дить значения потоков нейтронов в точках сетки, которая является неравно-

мерной в каждой зоне и рассчитывается программой по формулам § 9.7. По

одногрупповой программе вычисляются все три четных момента решения, по

многогрупповой решаются задачи с заданными источниками и задачи на /г

ф-

По программе РЕКИНУР находится численное решение многогруппового

уравнения переноса в бесконечном многозонном цилиндре методом характерис-

тик (см. §9.7, 9.8) при краевых условиях (5.3.6). Для ускорения внутренних ите-

417

раций в каждой группе применен циклический КР

(1)-метод (см. § 11.14, 11.15,

11.20);

в случае рассеяния вверх по группам применены итерации по Зейделю.

Программа позволяет решать задачи с заданным источником и на &

ф; в послед-

нем случае для ускорения внешних итераций применен чебышевский метод с

Г-последовательностью (см. § 10.32). Сетка по радиусу и угловым переменным яв-

ляется неравномерной, она строится по формулам § 9.7. В качестве начального

приближения к решению уравнения переноса программа находит численное ре-

шение многогрупповых уравнений в Pi-приближении. Разностная схема для Р

уравнений строится по формулам § 7.4. Программа может выдавать не только

значения ф

(/"), q>i (/*), но и само решение

(/•, ц, у).

Сферическая геометрия.

Для этого случая С. И. Коняевым составлены следующие программы.

10.

Программа решения кинетического уравнения для сферически-симмет-

ричной области в Pi-приближении. Препринт ИАЭ-2302, М., 1973.

11.

Решение кинетического уравнения для сферически-симметричной обла-

сти в Р

-приближении. Препринт ИАЭ-2517, М., 1975.

Программы 10, 11 предназначены для нахождения приближенного решения

одногрупповых уравнений Р

- и Р

-приближения в многозонной сферически-сим-

метричной области (см. § 6.2). Решается задача с заданными источниками. Раз-

ностная аппроксимация уравнений описана в

7.2, 7.4. Программы выдают чис-

ленные яначения всех моментов решения в узлах неравномерной сетки.

Все описанные выше программы написаны на языке АЛГОЛ и могут быть

запущены на любой ЭВМ, имеющей транслятор с АЛГОЛА. При этом потребует-

ся только заменить операторы, описывающие ввод и вывод информации и распре-

деление памяти. В программах коэффициенты уравнений и задаваемые источ-

ники предполагаются кусочно-постоянными по зонам. Входная информация

(полные сечения, сечения рассеяния, источники и т. п.) вводятся с перфокарт, по-

этому программы не связаны с какой-либо фиксированной библиотекой реактор-

ных констант. Каждый упомянутый препринт содержит текст программы на язы-

ке АЛГОЛ, описание и результаты расчета тестовых вариантов, включая машин-

ную печать.

§ П1.2. ОДНОМЕРНЫЕ ПРОГРАММЫ, ОСНОВАННЫЕ НА МЕТОДЕ

ПОВЕРХНОСТНЫХ ПСЕВДОИСТОЧНИКОВ

Плоская геометрия.

Для этого случая Н. В. Султановым составлена программа.

Одногрупповая программа расчета коэффициентов использования тепло-

вых нейтронов в плоской решетке с анизотропным рассеянием, ПРАКТИНЕП

(АР).—Атомная энергия, 1973, т. 34, вып. 6, с. 450.

В.

Ф. Бояриновым составлена программа.

Программа нейтронного группового расчета плоской ячейки реактора

НЕГР-П. Препринт ИАЭ-3142, М., 1979.

Программа ПРАКТИНЕП (АР) позволяет решать одногрупповое урав-

нение переноса методом поверхностных псевдоисточников (см. § 6. 5); рассчи-

тывать средние потоки по зонам, потоки и токи на границах зон, поглощение ней-

тронов в каждой зоне и коэффициент использования тепловых нейтронов в мно

гозонной плоской ячейке. В разложении индикатрисы рассеяния по многочле

нам Лежандра учитывается до пяти членов.

Программа НЕГР-П предназначена для решения многогруппового уравне

ния переноса с изотропным рассеянием методом поверхностных псевдоисточни

ков;

позволяет рассчитывать средние потоки по зонам и потоки на границах 3oi

в многозонной плоской ячейке в б^приближении (см. § 6. 5).

Цилиндрическая геометрия.

Для этого случая Н. В. Султановым написаны следующие программы.

Одногрупповая программа расчета коэффициента использования тепло

вых нейтронов в многозонной цилиндрической ячейке, ПРАКТИНЕЦ ЗФ. Пре

принт ИАЭ-2143, ИАЭ-2144, М., 1971.

418

Многогрупповая программа расчета многозонной цилиндрической ячейки

(приближенное разделение пространственно-угловой и энергетической перемен-

ных);

МГПРАКТИНЕЦ. Препринт ИАЭ-3376/5, М., 1981.

В.

Ф. Бояриновым составлена программа.

Программа нейтронного группового расчета цилиндрической ячейки

реактора НЕГР-Ц. Препринт ИАЭ-3377/5, М., 1981.

Кроме коэффициента использования тепловых нейтронов программа 3 рас-

считывает средние по зонам потоки нейтронов, потоки и токи нейтронов на гра-

ницах зон. Решается одногрупповое кинетическое уравнение методом по-

верхностных псевдоисточников, использующим цилиндрически-симметрическую

функцию Грина (см. § 5.6). Ячейка рассчитывается в G

и Gs-приближениях

(см.

§ 6. 5).

Многогрупповая программа 4 рассчитывает многозонную цилиндрическую

ячейку путем разделения пространственно-угловой и энергетической перемен-

ных, что позволяет свести многогрупповой расчет к решению одногрупповых

задач с последующим решением системы энергетических уравнений. Програм-

ма рассчитывает средние по группам и зонам потоки нейтронов, групповые пото-

ки нейтронов на границах зон, средние по группам интегральные потоки и сред-

ние по энергии сечения.

Программа 5 решает многогрупповое уравнение переноса с изотропным рас-

сеянием, она рассчитывает средние потоки по зонам и потоки на границах зон

в многозонной цилиндрической ячейке в G

- и б

-приближениях.

§ П1.3. ПРОГРАММЫ ДВУМЕРНОГО РАСЧЕТА

Расчет прямоугольных ячеек.

В.

Ю. Пляшкевичем составлена программа:

Решение кинетических уравнений в периодических решетках. Препринт

ИАЭ-2421,

М., 1974; ИАЭ-2549, М., 1975.

По программе методом Галеркина проводится двумерный расчет потока нейт-

ронов и средних потоков по зонам в многозонной прямоугольной ячейке с

цилиндрическими и прямоугольными зонами в четырехгрупповом кинетическом

приближении при заданных источниках. Ячейка предполагается симметричной

относительно центра; граничными условиями являются условия периодично-

сти;

источник, сечения и рассеяние предполагаются изотропными и кусочно-по-

стоянными; при этом рассеяние нейтронов в верхние группы отсутствует.

Поток нейтронов находится из решения системы уравнений'переноса, запи-

санных в самосопряженной форме Владимирова (см. §5.1). Поскольку рассеяние

в верхние группы отсутствует, задача сводится к решению четырех неоднородных

односкоростных уравнений переноса, а каждое из уравнений решается методом

Галеркина, в котором пробные функции зависят только от пространственных пере-

менных (см. § 6.9). В этом случае системой уравнений Галеркина является систе-

ма вырожденных интегральных уравнений, которая решается с применением

квадратур для сферы (см. § 5.9). В качестве пробных функций взяты тригоно-

метрические и локальные функции, позволяющие лучше учесть поведение пото-

ков нейтронов вблизи неоднородностей. Подробности алгоритма содержатся в

§ 6.9.

Программа написана на ФОРТРАНЕ и пригодна для любой ЭВМ, имеющей

транслятор с ФОРТРАНА. При оперативной памяти ЭВМ не менее 32 К число

вводимых зон в программе не более 50 (общее число зон в ячейке может достигать

100);

максимальное число пробных функций в разложении в каждой группе 82,

число различных веществ в ячейке не выше 10. Количество арифметических

действий при решении задачи зависит от числа пробных функций, числа угловых

направлений, числа зон в ячейке и пропорционально числу групп. При вводе

входной информации учитывается симметрия ячейки относительно центра.

Программа RZ-1.

Программа создана Г. И. Курченковой.

Метод Галеркина для диффузионных уравнений. Часть III. Программа

RZ-1.

Препринт ИАЭ-2280, М., 1973.

Она позволяет решить методом Галеркина двумерную двугрупповую зада-

чу диффузии нейтронов в геометрии (г, г); получить &

ф, распределение нейтро-

419