Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов

Подождите немного. Документ загружается.

а при г = R вычисляем:

5+Ф

+ ^

/2 + ЗУ

/4;

5(/?) = S

+ S^9

; /

+ф

1 = У

ф1/2 + (^/

/24-^/

)/2-/

(

1L20

)

Гф

=Гф

+ Зяу

]/Г=7

/4.

Пользуясь уравнением баланса (9.7.7) и подставляя в него ф

Фо

= <Pj> ф! (0) = 0, находим ф£ (г) при 0 < г < #. Для контроля

точности расчета вычисляем величину ф£ (R) = (1 — и) /+Ф

—

— V

/4 + VV2, являющуюся приближенным значением ф! (R), и ве-

личину

e=(j/

rrfr + «(Vo/2-Vi)/2j/( |(1-с)Ф&гЛг +

+ (l-x)/R/

q> (/?)). (11.20.10)

Величины ф

(#) и б используем для оценки точности решения.

При хорошей точности должно быть: ф£ (R) « ф{ (/?), б « 1.

Описанный процесс итерации повторяется при k = 1, 2, ..., ве-

личины g в уравнениях (11.20.1) циклически меняются с некоторым

периодом N согласно формулам § 14, 15.

В качестве начального приближения ф£, ф? берут соответственно

функции w, v, получаемые в результате решения краевой задачи

(11.20.1), (11.20.4) при g= i/з, JJV =

—

/4 + VJ2, если за F

(г)

*ф

(г) взять соответственно нулевой и первый моменты функции

/ (г, |i

Y);

функции 7ф°, У

ф° вычисляют из представления (11.20.3)

Небольшая модификация описанного /СР^метода состоит в вы-

числении по особым формулам величин ф* (R), которые путем ис-

пользования краевого условия (5.3.6) рассчитываются только через

значения S

, 7\р

, представляющие конечный итог итерационного

шага. Тем самым осуществляется некоторая экстраполяция по k

изменения величины ф§ (R). Это выгодно делать, например, при ра-

счете ячеек, где результаты итераций, как правило, медленнее всего

стабилизируются на внешней границе. В свою очередь, краевое ус-

ловие (11.20.7) достаточно эффективно выводит решение при г = R

на требуемую величину, несмотря на то, что в каждой операции К

краевые условия выполняются лишь приближенно. Вариант КР-

метода с точным выполнением на каждой итерации краевых условий

зеркального отражения описан в

[119].

Разностные аппроксимации

операции К содержатся в

9.6—9.8, а разностные аппроксимации опе-

рации Р

(1)

—

в § 7.4.

Многочисленные (начиная с 1962 г.) расчеты многозонных задач

со сложным распределением свойств сред по программам, составлен-

ным одним из авторов совместно с Е. А. Григорьевой, С. А, Фроло-

390

вой,

Ю. А. Власовым и С. И. Коняевым, показали высокую эффек-

тивность /(Pi-метода. Некоторые результаты расчетов для цилиндри-

ческой геометрии докладывались в 1964 г. на Третьей международной

конференции по мирному использованию атомной энергии в Женеве

[20].

Средняя скорость сходимости итераций, как правило, близка к

расчетной, вычисленной для модельных задач.

Приведем методический, типичный в определенном смысле пример

расчета ячейки, для которого метод простой итерации плохо сходится.

Константы выберем так, чтобы они качественно соответствовали свой-

ствам реальных ячеек и имели простой вид. Пусть

# =

х=1; а=1,09;

=0; )

2 = 1/2; 2

=1/4; /

-0 при 0<г<г

=1; (П.20.11)

2 = 2

=1/5; /

= 5 при r

<r<tf = 2. )

Возьмем 127 точек по радиусу, 126 характеристик, 8 угловых направ-

лений по у, в качестве начального приближения выберем Pi-прибли-

жение. После решения задачи окажется, что max ф

(/*) « 15,76;

Це°||

= тах|е°| « 2,82; б =

1,0007;

Ш = 0.

ОТ

\r=R

Задачу (11.20.11) решим циклическим КР± (1)-методом. Параметры

N, Р выберем из следующего условия: ошибка, оцениваемая по мо-

дельной периодической задаче при с = 1, должна уменьшаться при-

близительно в 1000 раз (этого вполне достаточно для расчета большин-

ства реальных задач). Поскольку имеем

ячейке две зоны

во внешней

зоне 2/S = 1, то априори трудно приписать е° определенному про-

странству типа Н (а, Р), в котором р характеризует закон убывания

коэффициентов Фурье а

пу

в разложении е° по нормированным соб-

ственным функциям ф

[а

(л

_|3

)].

Естественно предположить, что 8°

имеет ограниченные коэффициенты Фурье а

. Поэтому выберем р = 0.

Учитывая, что

= 7,2 . 10~

при а = р = 0 [см. (11.14.11)],

выбираем

= 4. Проследим за поведением величин

= max

ф*+

—

Фо I

(* = 0» !> 2, 3, 4). При N = 4, р = 0 имеем g

= 0,46, g

= 0,69, g

= 0,87, g

= 0,97. Для получения £

необходимо про-

делать пятую итерацию. Выполним ее при g

= 1. Расчеты пока-

зали,

что £

= 2,52,

= 3,4 . 10"

, g

= 4,9 • 10~

, 1

= 8,7 • Ю"

= 2,5 • 10~

. Следовательно, || £

е°

= 8,9 • 10~

, что близко

к У

— мажорантной оценке для периодической задачи.

На разбираемом примере поучительно показать разницу между

постановками и результатами решения проблем оптимизации ите-

рационных методов на классе задач (чем мы обычно занимались) и на

отдельной задаче. Пусть мы решаем задачу (11.20.11) циклическим

КРг (1)-методом при N = 4, в котором g

выбраны по формулам

(11.15.7), где р — некоторый параметр. Требуется выбрать р =

= Р

опт

таким, чтобы величина | |

| была минимальна. Видно, что

в такой постановке задачи исчезла связь р с пространствами Н (а, Р).

Величины g

выбираются по определенным формулам, асимптотиче-

ский характер которых становится неясным при фиксированном N.

391

От этих формул требуется лишь, чтобы они были разумными для

какого-нибудь пространства ошибок и какой-нибудь (пусть неудоб-

ной для численной реализации) метрики, в которой оценивается

ошибка [пример тому — пространства Н (а, |3) и функционал (11.14.6)].

Очевидно, что мы имеем совершенно другую задачу оптимизации. Для

нашего примера получаем:

Ропт =

—3,08;

при этом g

= 0,19, g

= 0,47,

ffs = 0,76, g* = 0,95, t

= 3,22,

= 3,9 . 10"

2 r

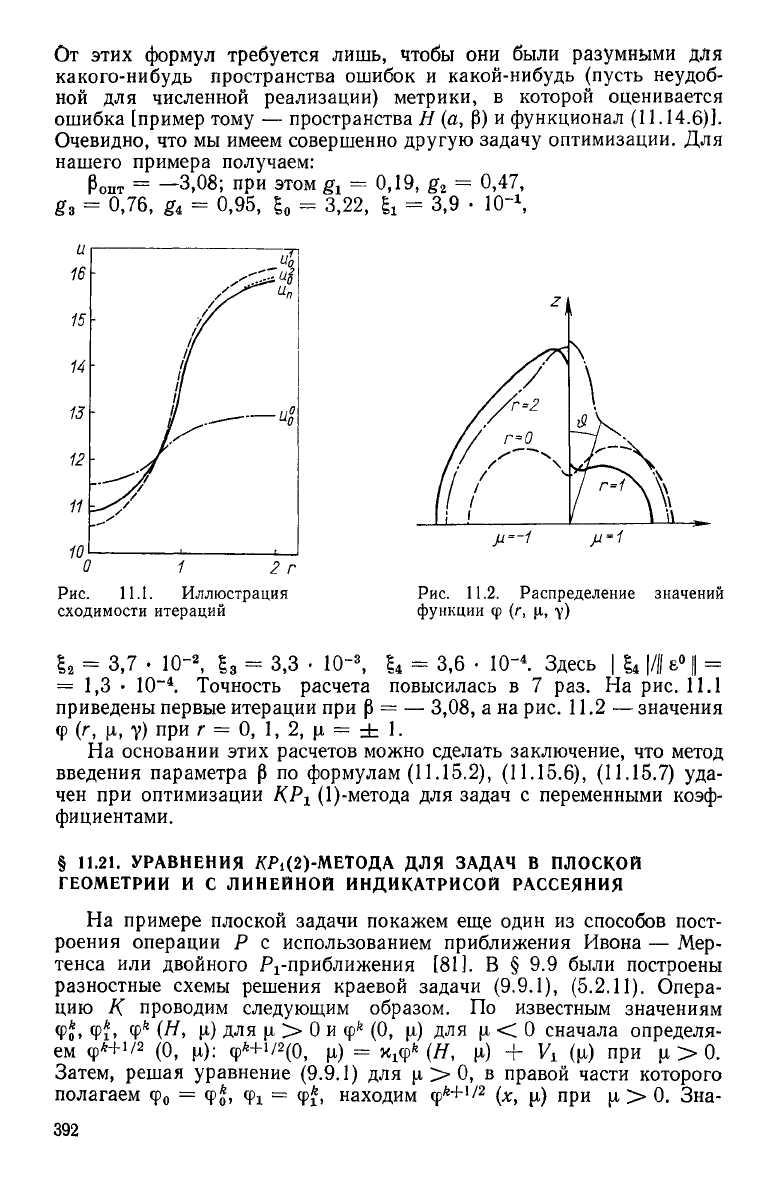
Рис.

11.1. Иллюстрация

сходимости итераций

-1К

/А*

-1К

Г=0

1: / \

11 '

1. \ \\ >

р=-1

= 1

Рис.

11.2.

Распределение значений

функции

ф (г,

(А,

у)

U = 3,7 . Ю-

, t

= 3,3 . 10~

, U = 3,6 . Ю-

. Здесь | £

\1\\

в° || =

= 1,3 • 10~

. Точность расчета повысилась в 7 раз. На рис. 11.1

приведены первые итерации при р = — 3,08, а на рис. 11.2 — значения

(г, |i, Y) при г = 0, 1, 2, |х = ± 1.

На основании этих расчетов можно сделать заключение, что метод

введения параметра р по формулам (11.15.2), (11.15.6), (11.15.7) уда-

чен при оптимизации КР± (1)-метода для задач с переменными коэф-

фициентами.

11.21.

УРАВНЕНИЯ ЯР1(2)-МЕТОДА

ДЛЯ

ЗАДАЧ

ПЛОСКОЙ

ГЕОМЕТРИИ

И С

ЛИНЕЙНОЙ ИНДИКАТРИСОЙ РАССЕЯНИЯ

На примере плоской задачи покажем еще один из способов пост-

роения операции Р с использованием приближения Ивона — Мер-

тенса или двойного Pi-приближения [81]. В § 9.9 были построены

разностные схемы решения краевой задачи (9.9.1), (5.2.11). Опера-

цию К проводим следующим образом. По известным значениям

Фо> Ф1»

Ф*

(#» I

) Д

ля

|ы

> 0 и ф^ (0, \х) для

\х

< 0 сначала определя-

ем ф*+*/

(0, \х): ср*+|/2(0, |х) -

<р

(Н,

|х) + V

(у) при |i>0.

Затем, решая уравнение (9.9.1) для \i > 0, в правой части которого

полагаем ф

= ф£, ф

= ф*, находим ф*+*/

(#, \i) при

\х

> 0. Зна-

392

чения этих функций используем для вычисления ф*+

(х) и запоми-

нания ф*-и/

(Я, \i). Такой же цикл совершаем для

\х

< 0: полагая

фАг+1/2 ^ ^

= Х1

ф/г (о, ^) + V

(|ы), находим <p*+i/2 (х, \I) при

jx < 0, по этим значениям заканчиваем вычисление ф*+*/

(х) и запо-

минаем

ф*+

(0,

\л)

при ^ < 0; из уравнения баланса (9.9.5) по функ-

ции

ц)

находим функцию ф^+

1/2

После проведения описанной операции К ошибка ц

(х

|я) =

= ф — фН-

удовлетворяет уравнению (9.9.1) с функцией

/(х,|1) = 2

[ф{+

-Ф* + 3|г|х(ф*+»/2-ф})]

и краевыми условиями

— Ф*(7/, |x)]

ц>0;

^+1/2(я,

[

х) = х

^+1/

(0,^) + х

[ф^+

(0,[х)-

-ф*(0,ц),

(А<0.

(11.21.1)

(11.21.2)

Для операции Р

можно взять уравнения из§ 11.18 или уравнения Р

приближения. Напишем уравнение двойного Р

приближения для

ошибки. Уравнения для ошибки с источником (11.21.1) умножим на 1

\х>

проинтегрируем полученные уравнения сначала в пределах от 0

до 1, а затем от

—1

до 0 и в результирующих равенствах осуществим

замену

Т)

^+1/2

+1/2(

+ [Х

+1/2(

л:

)

при

,х>0;'

^wt+^

(x) + \iv

(x) при [х<0.

(11.21.3)

В итоге получим систему четырех дифференциальных уравнений для

определения функции w

X12

, t;±"

1/2

, которая (если опустить ин-

декс k + 1/2 у функций) имеет вид

dw.

dv,

dx 3 dx

1 dw.

-Е(ш

+ у^)=2Лф

±^ф

|+^

;

dv.

dx dx

2 ±

v± =

^(±y<Po + l*<PiW/±>

(11.21.4)

где

= [w

+ ш_ + (t>

—y_)/2]/2;

Ф!

[(o>+

— a»_)/2 +

(»+

+ o_)/3]/2;

[Ф?

-Ф5±311(Ф*

-Ф*)/2];

/± = 2Л±(ф§+

1/2

-ф?)/2+?Г(ф*+'/2-ф*)].

(11.21.5)

Подставляя значения т]*+

1/2

, выраженные формулами (11.21.3),

в краевые условия (11.21.2), умножая их на 1 и ц, интегрируя первое

393

из полученных уравнений по отрезку [0, 1], а второе — по [—1, 0],

находим

<+'/

(0) + (1/2)о*+

(0) = х

К+'/

(Я)+ )

+ (1/2)<+>/

(//)]+х

|[ф*+'/2(Я,ц)-Ф*(Я

)

(г)]^;

(1/2)ш*+

(0) + (1/3)у*

'/2(0) = к

[(1/2)ш*

(Я)+ I

+ (1/3)^

+'/2(Я)] +

[Ф*+'/

(Я,Ц)-Ф*(ВД]М*;

о |

,*+1/2(Я)_(1/2)У1+

(Я)-К

[Ш1+

(0)—

-(1/2)и*_+'/2(0)] + х

f [ф*+'/

(0,ц)-

*(0,|А)]ф;

— 1

—(1/2)^_+

(Я) + (1/3)^_+

(Я) = х

[-(1/2)^+

(0) +

+ (1/3)^_+

(0)] + х

f l<f

v)—Ф

(0, |х)]|id|*.

-1 j

(11.21.6)

Решая краевую задачу (11.21.4)—(11.21.6) методом прогонки,

вычисляем значение qTj+

l/2

= (1/2) [о;

+ ш_ + (v

—

v_)/2]

и полагаем

*+1 =

фН-1/2

JftH/2;

Ф^

(Я,

х)==ф

(Я,

х)

+ <+

(Я) + ^

+1/2

(Я), ji>0;

ф^

+ 1(0,

(

г)

ф^

(0,

л)

+ ^_+

(0) + ^+

/ (0), \л<0.

Функцию

ф^

(0) рассчитываем по квадратурной формуле, а

осталь-

ных точках функцию

ф{+

находим из уравнения баланса. Затем пов-

торяем описанный цикл итераций.

11.22.

РЕШЕНИЕ КИНЕТИЧЕСКОГО УРАВНЕНИЯ

МЕТОДОМ РАСЩЕПЛЕНИЯ

Рассмотрим нестационарное односкоростное уравнение

±^.

уф +

2ф

= -|^ |

(х,Й',0^'+/(х,Й,0. (П.22.1)

Для уравнения (11.22.1) поставим смешанную задачу Коши:

Ф (х, Q, *) = 0 при Йп<0, х, t € Y, (11.22.2)

(х, Q, 0) = Ф (х, О), х, Q 6 D X Q (11.22.3)

в цилиндрической области П

D X Q X 7

с основанием D X Q

и боковой границей у = Г х Т. В этом параграфе используем обо-

значения § 5.1.

394

Наряду

нестационарной задачей (11.22.1)—(11.22.3) рассмотрим

стационарную задачу (5.1.4), (5.1.6) при

(|х

)

= 1.

Решение

ее

будем

искать

классе

(см. § 5.1.). Для интегрирования задачи (11.22.1)—

(11.22.3) используем схему расщепления

[171]

(ф*+1/2 —

*)/т +

(аф*

+ 1/2

А) = /; (П.22.4)

(фй4-1_

+ 1/2)/

(аф^+1+(Зф^+1/2) = 0, (11.22.5)

где

= 2/ —

Q6 — разностные аппроксимации

опе-

раторов

= 2/

dQ', А

QV соответственно;

— аппрок-

4яо

симация

/; т = vAt; а > 0; Р>0; а + Р = 1.

Расщепляя оператор второго дробного шага, получаем схему

полного расщепления

(ф*+1/4—

*)/т +

(аф*

Рф*)

= /; (11.22.6)

(

^(s+l)/4_

^ + s/4)/

T + Lis

(^ +

+ l)/4

^ + s/4)

= 0)

(Ц.22.7)

где

= L

+ ^i

^1з'»

^ii

— аппроксимации одномерных

one-

раторов

-з~г» i = 1, 2, 3.

Основная цель наших исследований —

решение стационарной задачи (5.1.4), (5.1.6). Сформулируем некоторые

свойства операторов

и Л

пространстве

(D X fi).

Лемма

11.22.1.

Оператор

при 2

= 2 — 2

положитель-

но определен.

Лемма 11.22.2. Оператор

является

положительным.

Лемма 11.22.3. Оператор

(/ +

TAJ)"

существует

ограничен

из

X Q) в D

л/ш<юи

II(/ +

F||<(1

— exp

(—dh))

\\,

£ L

(D X Q), где d

—

диаметр

области

Рассмотрим теперь самосопряженную формулировку задачи (5.1.4),

(5.1.6).

Для этого уравнение (5.1.15) вдоль характеристик

х' = х

—

£Q

запишем

виде (9.6.19):

L±J!L + 2

= -b.

Ftx

(11.22.8)

где

F = ^2, а

функция

и (х' + £Q, й)

удовлетворяет граничным

ус-

ловиям:

du/dt

+ 2u\

_Q =

0;\

du/dl-Zu\

= 0. j

(П.22.9)

Рассмотрим операторы

Л(

"1Г 2"^Г

+2о/; Л

2 =

з(/-Я (11.22.10)

где штрих означает,

что

операторы

Л{ и

связаны с задачей (11.22.8),

(11.22.9). Отметим свойства операторов Л( и Лг.

Лемма 11.22.4.

Оператор

А{

положительно определен

при

^ 0.

Лемма 11.22.5. Оператор

Аг

положительно

полуопределен.

Утверждения лемм 11.22.1—11.22.5 являются следствиями резуль-

татов работы

В. С.

Владимирова [41]. Кроме перечисленных свойств

395

отметим следующие свойства операторов Л

и А'

: они ограниченные

и самосопряженные

, причем преобразуют любую функцию

из Ь

снова

функцию

из

. При

= 0

оператор Л

становится положи-

тельно полуопределенным.

Введем

линейном множестве

Т>

соответственно

норму,

положив llcpHi

||(/

TAJ) ф||; фб D

;

||ср||

||(/

ТЛ0Ф1|;

ф^

и отметим неравенства ||<р||

(1 — ехр (—dlx)) ||<p||i;

(1 — ехр

{—dlx))

||ф||

;

ф € D

Норма

понимается

как

норма

пространстве

Отсюда

из

сходимости

в D

(соответст-

венно

) вытекает сходимость

в L

Принимая, что область опре-

деления оператора

составляют функции множества D

область

определения оператора Л{ — функции множества

краевую

за-

дачу (5.1.4), (5.1.6) можно записать

виде

(Л

+Л

)ф

= /,

(11.22.11)

а краевую задачу (11.22.8), (11.22.9) —

виде

(Л(+Л0ф

= /.

(11.22.12)

Для решения задачи (11.22.11) построим итерационный метод

Ф*+1«Ф*_атВ(Лф

—/); Л

, (11.22.13)

где

= [(/ +

тЛ

)

(/ +

TAJ]-

, (11.22.14)

а,

— итерационные параметры. Формальная подстановка вместо

иЛ

операторов

Л1

иЛг

соотношения (11.22.13)

(11.22.14) дает

итерационные методы

для

решения задачи (11.22.12). Докажем схо-

димость метода (11.22.13)

решению задачи (11.22.11) или (11.22.12).

Для дальнейшего анализа нам потребуется

Лемма 11.22.6. Если 0

ос

оо и

оператор

удовлетворяет

условию

(А

ф, ф)

^ 0

для всех ф, тогда

существует

(О

< у <

1),

такое,

что для

каждых

а < х

< р

оператор

I +

А имеет

обратный

и ||(/ —

А)

(I +

Л)

-1

< у.

Если оператор

огра-

ничен

и (А ф, ф) > 0,

то

у < 1.

Доказательство. Существование оператора

(/ +

t^)"

следует непосредственно

из

условия

(А ф,

ф)

0. Обозначим

= (I -

А)

(I +

тИ)-

; ф

= (/ +

АГ\,

(11.22.15)

тогда имеем

||Q||»

sup

(Q(p>Q(p)

=sup (V—4*W>V-xiA)W

^о (ф, ф)

ЪФО

((/ +

Л)г|?, (/+т

Л)г|>)

(^^)-2t

^) + Tf

,^) (П.22 Л 6)

Очевидно, что если оператор

ограничен

и (А

1р, -ф)

0, то при всех

< р

выполняется неравенство

7 < 1.

Из лемм 11.22.1 —

11.22.5 следует, что операторыЛ^ЛьЛ^Л^ удовлетворяют условиям

леммы 11.22.6,

396

Лемма 11.22.7. При

всех

0 < т <i оо

||7?|^||(/-тА

)(/

тЛ

)-Ч/-^

)(/

тЛ

||<1 (П.22.17)

на

классе функций

д'И

\\(1-%АЬ(1 + %М)-Ч1-тА{)(1

хА{)-*Л1<1 (11.22.18)

на

классе функций

Доказательство. Докажем первое неравенство. Применяя

неравенство Коши

—

Буняковского, получаем

|| (/

—

тЛ

)

(/ +

+ тЛ,)-

(/ -

тЛ

)

(/ +

тЛ^-

< || (/ -

тЛ

)

(/ +

тЛ,)"

|| ||(/ -

—

rAj (/ + TAJ)""

!!. В

силу леммы 11.22.6, учитывая свойства опе-

ратора

1э

имеем ||(/—тЛ^

(I +

тЛц)"

< 1.

Рассмотрим норму

—

тЛ

)

(/ +

тЛа)"

С\\.

При 2

> 0

оператор

ограничен

и положительно определен, поэтому ||

—

тЛ

)

(/ +

^А

< 1,

что доказывает неравенство. Рассмотрим случай

= 0. При

этом

оператор положительно полуопределен. Согласно лемме 11.22.6,

||С||

1. По определению нормы

имеем

||С||=

sup ЛШ =

НФ|£О

НФИ

sup

((/-тЛ

) (7+тЛ

)-1

ф>

(7-тЛ,) (/ + тЛ

)-*

)

II Ф ||^о

(ф,ф)

№,

г!?)-2т(Л

г|>, Ч»)+т»(Л,Ч>, Л

г|?)

г|>

\\+о

(о|?,г|?)

2т(Л

я|>, t)+^

^,A

t|))

Из полученного соотношения следует,

что

равенство нормы еди-

нице может быть только

случае (Л

, гр, яр)

= 0.

В силу свойств опе-

ратора

это

эквивалентно уравнению

г|>

= 0.

(11.22.19)

Проанализируем пространство решений этого уравнения. При

имеем

(Ф —

Sip)

= 0.

Учитывая,

что 2

Ф 0,

получаем

г|)

—

Si|)

= 0, т. е.

г|) (х,

й) =

г|) (х). Таким образом, пространство

ре-

шений уравнения (11.22.19) не принадлежит классу D

, если г|э(л:)|г^

^0.

Случай i|?(#)|

= 0

требует дополнительного исследования.

Аналогично доказывается второе неравенство.

Основываясь

на

леммах 11.22.6

11.22.7, докажем следующую

теорему.

Теорема 11.22.1.

При

любом,

начальном приближении

ср° £ £>

< т <

оо,

0< а <

2 метод

(11.22.13) сходится

i->

единствен-

ному решению задачи

(11.22.11).

Доказательство. Проводя тождественные преобразования,

перепишем уравнение (11.22.13)

виде

Ф*-Н=7У+£, (11.22.20)

где

Т-

а/2)

/ +

(а/2)

Р-

тЛ^"

(/ +

тЛ,)-

(/ -

тЛ

)

—

тЛх);

g =

ат (/

rAJ"

тЛ

)

-1

Очевидно, что

является

397

линейным преобразованием и отображает множество D

в себя.

Пусть ф £ D

. Тогда

||Гф||

= ||(/ +

гА

)Гф||

= ||Г(1-а/2)(/ +

тА

)

+ (а/2)(/ +

тА

)-1

Х(/-гЛ

)(/-тЛ

)(/ + тЛ

)-Ч/ + ^Л

)]ф||<||,(1-а/2)/ +

+ (а/2) (/ +

тА.)-■

(/-тЛ

)

(/-тА

)

+ rAJ-

|| ||

(/ +

тЛ,) Ф ||

= ||(1-а/2)/ +

аЛ/2||

•

||ФIk- (П.22.21)

В силу леммы 11.22.7 получим ЦГ^ <

||(1 —

а/2) / + aR /2|| <

при 0 <а^2. Отсюда следует сходимость. Поскольку оператор Т

является сжатием с областью определения, плотной в L

, метод

(11.22.13) сходится к решению задачи (11.22.11). Теорема доказана.

Все доказательства мы проводили для уравнения переноса с изо-

тропным рассеянием. Легко видеть, что доказательства остаются в

силе при g = g (fA

) ф 1. Действительно, в предположении неизо-

тропности рассеяния справедлива

Лемма 11.22.8.

Оператор

= 2/—^lg(|i

)dQ' (11.22.22)

4я

положительно определен

при 2

>0 и

положительно полуопределен

при 2

= 0.

Доказательство. Рассмотрим соотношение

(Л

ф,ф)= Г 2(xH

(x,Q)dQdx

—

- J 2

(х) I±tg(

)cp(x,Q')dQ'U(x

Q)dQdx.

Применяя ко второму интегралу неравенство Коши

—

Буняков-

ского и учитывая условие нормировки индикатрисы, получаем

(Л

ф,

ф)

^ 2

0).

Полученное неравенство доказывает лем-

му. Следствием зависимости функции g (fi

) лишь посредством \i

является самосопряженность оператора Л

Полагая т = vAt, видим, что алгоритм (11.22.13) при а = 2 при-

меним для решения задачи (11.22.1)—(11.22.3). При этом оператор

Т = (/ + тЛ^"

(/ +

хА

—

) (/

—

тЛ

) является опера-

тором шага. Область определения оператора плотна в L

(D х Q),

Выполнение неравенства || Т

при любом т > 0 обеспечивает

равномерную ограниченность семейства операторов при всех / > 0.

Кроме этого, при выполнении условий леммы 11.22.6 имеет место не-

равенство

тЛ)-

(7+тЛ

< || (/ +

А,)'

||. ||(/

+ТЛ,)-

< 1

при любом 0<т<оо, ф £ D

. Указанные свойства оператора Т

гарантируют устойчивость счета. Непосредственная проверка пока-

зывает, что имеется аппроксимация по t. Тогда по теореме эквива-

лентности получим сходимость расщепленной задачи (11.22.11) к

решению нестационарной задачи (11.22.1) — (11.22.3).

398

При практической реализации алгоритмов численного решения

кинетического уравнения методом расщепления возможны различ-

ные схемы и их модификации. Общие принципы построения таких

схем и постановки граничных условий для схем расщепления обсуж-

даются в работе

[171].

Применим метод (10.12.15):

(/ + тЛ

) (/ + хА

)

(Ф*+

—

Ф*)

= — ат(Лср*—/). (11.22.23)

Введем вспомогательные функции ф

и ф

и представим уравнение

(11.22.23) в виде системы уравнений:

(/ + тЛ

)ф?+

=атг

;

тЛ

)<р5

ф*+ь

<р*+» =фЧ-ф5

(11.22.24)

где r

= f — Ay

— невязка. Интегрируя первое уравнение (11.22.24)

по всем направлениям ft, получаем

(1+т2

)ф?+

=ат^. (11.22.25)

После этого из (11.22.24) с использованием уравнения (11.22.25) на-

ходим

*+1=-

+ тГ

г!

s'o

г*

(11.22.26)

4л(1+т2

)

Второе уравнение (11.22.24) с граничными условиями решается как

соответствующая краевая задача для дифференциального уравнения.

Задачу для него можно записать в виде

ftV*|> + ip/т = g/т; ф|

= 0; Пп < 0, (11.22.27)

где i|) = ф*+

, £ = Ф?

Введем в рассмотрение формальный параметр I и задачу (11.22.27)

дополним следующей:

дгр

&|>

ду дг

j>|r =

Йп<0.

(11.22.28)

dl ' * дх

Нетрудно убедиться, что решением задачи (11.22.27) является функ-

ция

= J $ ехр

(—£/т)

dl. (11.22.29)

Уравнение (11.22.28) допускает расщепление на одномерные задачи.

С этой целью интервал 0 < | < £

разобьем на частичные интервалы

шириной Д£ = 1

р+

1 — 1

Тогда

9*i

-Qi

dti

дх

itf = $";

ду

;?+!.

■O,^t.-0;

$ = $

(11.22.30)

399