Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов

Подождите немного. Документ загружается.

Решение задачи (11.22.28) i|)P

найдется

из

соотношения ty

p+1

Полученная система дифференциальных уравнений

(11.22.30)

частных производных позволяет найти решение задачи

(11.22.28)

на

системе точек

Продолжение искомого решения

на

всю область проводится

помощью подходящих квадратурных фор-

мул.

Для оценки сходимости

на

периодической задаче (11.1.4) иссле-

дуем несколько модифицированный метод. Модификация заключается

в том, что метод простой итерации (операцию К) будем чередовать

ме-

тодом расщепления (принимая, таким образом, этот метод

за

опера-

цию

). При

таком способе итераций удается сравнительно просто

получить рекуррентные соотношения между нулевыми моментами

по-

следовательных приближений,

ибо в

этом случае ошибка после опера-

ции

принадлежит классу функций вида (11.1.15). Поскольку опе-

рация

сама уменьшает ошибку,

то,

получив формулы

для

ошибки

предлагаемого метода, найдем оценку снизу

для

скорости сходимости

метода расщепления.

Операторы Л

для л-го

коэффициента Фурье

определим

как

= Р (пй)

1 — с\

= с

— S).

(11.22.31)

Выполняя операцию

(11.1.11), получаем u

1/2

где, как

всегда,

fon

применяя метод расщепления, находим u

k+l

из

формулы

)(I

=(I-xA

)(I-xA

+2xF. (11.22.32).

Получим формулы

для

ошибки

г)

(х, Й) в

методе (11.1.11), (11.22.32)

Для этого

(11.1.11), (11.22.32) положим

F = 0:

£+1/2^(/+/2 (пй)

)-1се£; (11.22.33)

(/ + тЛ

) (/ + хА

) т|*+1 = (/- тЛ,) (/

-TAX)4*+

Учитывая (11.22.31), получаем

[I+xc(I—S)][I +

T(P(nQ)

I—C)]TI*

=/*

1/2

(П.22.34)

где

= [/—тс(/—S)][/—т(/>Й)

+ /

—с)]т|Л+1/

(П.22.35)

Введем функцию

i|)n

определяемую равенством

+ т(/

(п,Й)

/—

с)]т|*

я|)*+».

(11.22.36)

Тогда

+ xc(I—S)]^+i=/^+i/2. (11.22.37)

Уравнение (11.22.37)

—

интегральное с вырожденным ядром; его

решение находится известным способом. Применяя к (11.22.37) опе-

ратор S и учитывая, что S

= S, получаемой"

= /оп"

1/2

, а значит,

<1>п

= (1 +ТС)""

(/n

+1/2

+ Tc/g+

I/2

). Из (11.22.36) получаем

=(l

TC)-41+T(/

(nQ)2+l_c)]~l(^+l/2+ ТС^+1/2).

(11.22.38)

400

Но так как из (11.22.35), (11.22.34) следует, что

/J+»/2 +

TC/*+l/2=iC(l—TC

2TCS)[1—т(Р(пО)»+1—с)]

Х(1+/>Й)2)-1

то из (11.22.38) находим соотношение между r)n

и е£, применяя к ко-

торому оператор 5, получаем 8n

= сТ (I |п|) е„, где

Г(Лп|) =

+ тс)-^[(1+т(/»(пО)«+1-с))-ЧИ-те) +

+ 2TcS][l-T(/

(nfl)

l-^)(l

+ /2

Q)2)~i

(Ц.22.39)

Обозначим

= / |п| и применим формулы суммирования по

сфере (5.1.36). Тогда

T{t)

= ±=^-

fu+t^^

i-^i-Ml-t^^+l-cMx

1С

, J

X(l +

+ 7V

-f[

+T(/

+l-c)]--

(

f[l—T(<«|i»

+ 1—сИО+^ц")"

Вычисляя интегралы, находим

T(t) = r(t)- *П-«г(01

l + t(l-c)

+ т(1—с) J

(11.22.40)

Исследуем поведение функции Г(/) при фиксированном значении

т>0ис-> 1—0. Предельная функция Т

(t) = lim Т

(t)

имеет вид

с-*1

— 0

7\ (*) = г (t)—2 х И—г

(t)]r

(tVn). Очевидно, что Т

(t)

< г

(t)

< 1,

(0) = 1 и Т

— 8

при достаточно малых / > 0, где

8 > 0

—

любое наперед заданное число. Проверим, выполняется

ли условие

{t)>

—

1. Оно эквивалентно требованию

(l+r(t))/(l-r(t))>2Vrt-

avctgtVx. (11,22.41)

Зафиксируем некоторое t > 0. Тогда найдутся такие достаточно

большие т > 0, что условие (11.22.41) выполнено не будет, а тогда

7\0)<-1.

Подводя итог проведенному анализу, можно сделать следующее

заключение: а) если метод расщепления сходится при некотором фик-

сированном т>0, то его сходимость замедляется при с->1—0;

б) существуют такие достаточно большие т

0, что метод расщеп-

ления при значениях с, достаточно близких к единице, расходится.

401

Потребуем теперь, чтобы метод был балансным, т. е. чтобы нуле-

вая гармоника определялась им точно IT (0) = 0]. Тогда получим

т = (1 _ с)-

, а

T{t) = r(t)—

СГ(

*\ ^arctglfll—

g)-'/2].

(11.22.42)

o-<r

Зафиксируем любое t > 0. Из (11.22.42) видим, что для любого М > 1

найдется б = б (*) > 0, такое, что —Т (t) > М при 0 < 1 — с <

< б (/),

> 0. Это значит, что балансный метод расщепления расхо-

дится при значениях с, достаточно близких к единице.

Итак, найден метод, который сходится для краевой задачи, рас-

сматриваемой в начале параграфа, и расходится на периодических

задачах при достаточно близких

единице значениях с. Этот факт яв-

ляется достаточно убедительным аргументом в пользу того, что пе-

риодическая задача является серьезным испытанием для итерацион-

ных методов. Исследуя в § 11.23 аналогичный метод для несамо-

сопряженного уравнения, убедимся, что для него расходимости нет.

Таким образом, здесь имеется полная аналогия с методом итерацион-

ных отклонений (см. § 11.3), примененным к самосопряженному и не-

самосопряженному уравнениям.

§ 11.23. О НЕКОТОРЫХ МОНОТОННЫХ СХЕМАХ РАСЩЕПЛЕНИЯ

Для кинетического уравнения переноса Г. И. Марчуком и

У. М. Султангазиным [173, 224] предложены монотонные схемы рас-

щепления, при которых решения остаются в классе положительных

функций. Рассмотрим эти схемы применительно к кинетическому

уравнению для плоской геометрии (11.5.1) при следующих условиях:

(0, in) = 0, fi > 0; ф (Я, \i) = 0,

\х

< 0. (11.23.1)

Введем операторы

x-^; Л

= 2/—^- f d\x. (11.23.2)

При этом уравнение (11.5.1) запишется в виде (11.22.11). Обозначим

D (A

) область определения оператора Л

1в

Здесь D (А

) есть класс

функций, суммируемых с квадратом вместе со своими производными

первого порядка по х и удовлетворяющих граничным условиям

(11.23.1). Пусть f (дг, |х) G D (AJ.AJ £ D (А

). Тогда задаче (11.5.1),

(11.23.1) можно поставить в соответствие нестационарную задачу

д$№ + (А

+ Л

) ф = 0, ц;.о = f (*, Ц). (11.23.3)

Решение задачи (11.23.3) связано с решением исходной стационар-

ной задачи следующим образом:

Ф(*.

rt-!♦(<.*. |0 Л (П.23.4)

402

Оператор Л

является производящим оператором^сжимающей полу-

группы S. Тогда любое решение г|> (t) £ L

(0, оо) удовлетворяет

интегральному уравнению

оо

у (J) = S (t, 0) /

—

J S (/, т) Л,* (т) А. (11.23.5)

Для приближенного построения решения последнего уравнения

рассмотрим задачу

$(0Н/; -^- + Л^ =

$(**) = $(/»)—£-***('*>; (П.23.6)

*(<*

i) =

4»(/*

i)~|-Ai

*(/*

i).

(U.23.7)

На первом шаге в промежутке 0 < t < т решается задача Коши

А-

+ А

$ =

й(0) = /(*,|*)--5-Л,/(*,ц).

На втором шаге в этом же промежутке решается интегральное урав-

нение (11.23.7). Затем процесс определения tj> (t)

(t)

повторяется

по

схеме (11.23.6), (11.23.7). Функция-ф(^), построенная таким образом,

является решением задачи (11.23.6).

Исключая tj) из уравнений (11.23.6), (11.23.7), получаем

^(/

fe+1

) = S(/

ft+1

,M^(4)-

-y[S(/

ft+1

^(/

)+A

^(/

ft+1

)]. (11.23.8)

С другой стороны, из уравнения (11.23.5) вытекает

fc+

= S

fc+lf

)- f

(4+i,

т)

ф (т)

dr. (11.23.9)

Сравнивая (11.23.8) и (11.23.9), можно установить, что уравнение

(11.23.6) имеет второй порядок аппроксимации пот.

Теперь исследуем устойчивость решения задачи (11.23.6). Для

этого (11.23.8) запишем в виде

(*»+i)

)

[(l

-i

2)$(/

)

+ ^ j $ ft)

<*,*]

—I

Отсюда

TS/2)

$ (f

fc+1

)

-tS/2)

k+b

) $

)

403

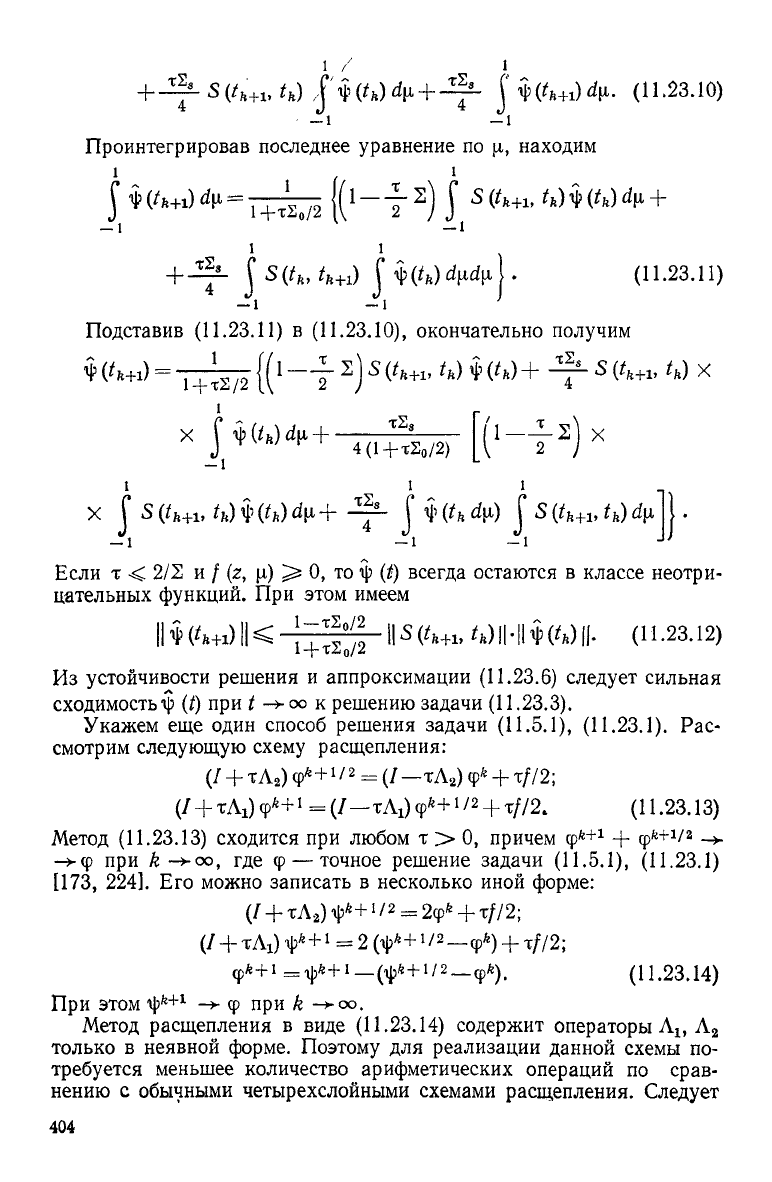
1 /■

S(t

h+1

) $*(t

)d)i + -&- j *(**+,)ф. (11.23.10)

~1 -1

Проинтегрировав последнее уравнение по

JA,

находим

(

d|i

Y^^

- у 2) J s

fc+1

)

-i —i

i i

, T2,

jS(/

ft+1

) J$fo)d|id|il. (11.23.11)

—

i '

Подставив (11.23.11) в (11.23.10), окончательно получим

-1

-^3r[('-T

)

1 1

X j S(/

k+1

)${t

)dvL+

-^- J ф(**40 j

Sft

)dJ}.

-1 -1 -1 J'

Если т < 2/2 и / (г, |i) ^ 0, то

гр

(t) всегда остаются в классе неотри-

цательных функций. При этом имеем

||*(Wll<

~ll°?9 4

^+ь WN(W (11.23.12)

Из устойчивости решения и аппроксимации (11.23.6) следует сильная

сходимость

$ (/) при t ~>оо к решению задачи (11.23.3).

Укажем еще один способ решения задачи (11.5.1), (11.23.1). Рас-

смотрим следующую схему расщепления:

+ тЛ

)ф^+

-(/-тЛ

)ф^ + т//2;

+ тЛ

)ф

=(7—TAJ<p

+ xf/2. (11.23.13)

Метод (11.23.13) сходится при любом т > 0, причем <р

Л+1

k+1/

->-

->Ф при k ->оо, где

ф —

точное решение задачи (11.5.1), (11.23.1)

[173,

224]. Его можно записать в несколько иной форме:

+ тЛ

)^+

2ф^

т//2;

+ тЛ

)^+

=-2(^+

—ф^) + т//2;

<p*+i

^+1_(^+1/2_

(11.23.14)

При этом

\|)

fe+1

->• ф при k ->оо.

Метод расщепления в виде (11.23.14) содержит операторы Л

, Л

только в неявной форме. Поэтому для реализации данной схемы по-

требуется меньшее количество арифметических операций по срав-

нению с обычными четырехслоиными схемами расщепления. Следует

404

отметить, что при некоторых ограничениях на т можно добиться моно-

тонности схемы.

На 2я-периодической задаче для уравнения

IQV ф + ф = cS ф + /

с постоянными / и с исследуем сходимость /СР

метода, в котором

в качестве операции Р

взята схема расщепления (11.23.14). В (11.23.14)

можно с помощью тождественных преобразований исключить функ-

цию ф

. Тогда для функций i|)

fe+1

, i|)

получим уравнение

+ тЛ

)(1+тЛ

)г|)Н-1

(1_тЛ

)(1-тЛ

)^ + 2т/, (11.23.15)

гдеЛ

= / — с5,Л

= /Q V.

Проследим за поведением ошибки г\

= ф — г|)

и нулевого мо-

мента е

. Пусть i|)

, &

заданы. Тогда после операции К получаем

T|^

1/2

= c(l + i/nQ)-4*; e£

+1/2

= cr(0e£; t = l\n\. (11.23.16)

Если результат операции К использовать в уравнении (11.23.15),

подставив его вместо функции i|)

, и найти таким способом функцию

то уравнение, связывающее ошибки r\

{

и г]*-И/

, будет

иметь вид

(1+тЛ

)(1 +

тЛ

=(1—

тЛ

)(1—

тЛ

)^+1/2

(Ц.23.17)

Найдем г)^

из уравнения (11.23.17), считая, что r\

{

задано фор-

мулой (11.23.16). Имеем (1 — тЛ

) (1 — тЛ

)

= ifc, где

^1п = [(1-т)(1 +

т)/(1

1/пЙ)-т(1-т)

тс(1

+ т)г(/)-т

с]сб^

Пусть

я|>

= (1 +тЛ

)т|*+

. (11.23.18)

Тогда

(1 + т (1 — cS))

Ч>2

= 4>i. (11.23.19)

Уравнение (11.23.19) — интегральное уравнение с вырожденным яд-

ром. Его решение имеет вид

1дД

-^Г

<'-*>('+*> -

T)+

2Tg((1+T)r(/)

+ т L

i/nO

+ т(1—с) J

Наконец, решая уравнение (11.23.18), находим

т)*

+х

а по r\

k+1

вычис-

ляем e

k+1

=сГ(/|п|)е*;

T(t) = г (t) - 2т [1 - cr (t)] г (т*)/(1 + т (1 — с)). (11.23.20)

Сначала исследуем поведение функции T(t) при фиксированном

значении т>0ис->1-0. Предельная функция Т

(t) = Hm Г (f)

с-»-1—0

имеет вид 7\ (t) = г (*) — 2т 11 — г (*)] г (т#). Видно, что при

достаточно малых t функция Т

(t) близка к единице, а Т (0) = 1.

Следовательно, сходимость метода замедляется при с->1—0 и при

любом фиксированном значении т > 0.

405

Потребуем теперь, чтобы при 0 < с <

метод был балансным, т. е.

чтобы Т (0) = 0. Из последнего требования получим, что на т и с

должна быть наложена связь т = (1

—

с)"

Исследуем поведение

функции Т (t) при этом условии:

T(t) = r

(t)

—

[1 — cr

(/)] t

arctg (//(1

—

с)).

(11.23.21)

Из (11.23.21) следует, что

= 0;

(t) = lim Г(0 =

г->1

—о

я (11.23.22)

r(t)-f[l-r(t)]t~\ t>0.

Формула (11.23.22) показывает, что при достаточно малых t>0

(t)

1 —

е, где е > 0

—

любое наперед заданное число. С дру-

гой стороны, | Т

1 < 1. В самом деле, Т

(t)

< г (/), а если заменить

в (11.23.22) функцию г (t) меньшей 3/(3 +

то нетрудно получить

для Т

(/) оценку снизу —

< — К9+Зя

/(6

+ 3/я

+ (1/я) х

Х"|Л)+Зя

))< Т

(t). Следовательно, метод при т = (1

—

с)'

сходит-

ся,

но его сходимость замедляется при с

->■

1—0.

§ 11.24. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ РЕШЕНИЯ

КИНЕТИЧЕСКИХ УРАВНЕНИЙ

В настоящем параграфе изложены результаты Ю. А. Кузнецова

[105,

107, 108] по применению обобщенного метода сопряженных

градиентов для решения систем сеточных уравнений

Ли = /, (11.24.1)

построенных в

9.5.

Используя свойства матрицы А системы (11.24.1),

сформулированные в § 9.5, укажем конкретные способы выбора мат-

риц

и Я, которые обеспечивают А

А — самосопряженность и по-

ложительную определенность матрицы НА в пространстве U = (I —

-НА)Е

Общий случай. Используя разложение (9.5.30) (9.5.31), вы-

берем D = Н = L"

и покажем, что матрица L"

является самосопря-

женным оператором в пространстве

= (/

—

АН) Е

= SL^En =

= SE

(положительная определенность L"

в UA следует из поло-

жительной определенности L'

в пространстве £

), установим A

DA —

самосопряженность

положительную определенность матрицы АН

■=

= / —

Ь,~

в пространстве U.

Действительно, так как SL^S—симметричная матрица (см.

9.5),

то для всех

*ф

= Sv,

ср

= Sw из

(V,

— некоторые векторы из Е

)

имеем

(I-iг|>,

ф)

(Г"

Sv,§ w)=*{SI"

=.{v, Si"

Sv,

{Sv,

Sw) = fo

1-4) (11.24.2)

406

и, следовательно, L-» является самосопряженным оператором в U

Для доказательства АЧ) А -самосопряженности и положительной

определенности матрицы НА в пространстве V достаточно показать

что матрица АН является D-самосопряженным и положительно оп-

ределенным оператором в пространстве U

. Пусть

= §v

г|>

= Soy

некоторые произвольные векторы^ пространства U

(v, w £ Е

Тогда так как матрицы SL^S и SL^SL^S симметричны, то

(Л!-

ф)

-1 = (L-

{I-SL-*)

-ф»

) = (§Г-*&, ю)_

—

(Sl-»SX-»2to, ю) = (о, S (I-

—l^SZ-

) §ю) =(ф, /Шф)-^!

(11.24.3)

и, следовательно, матрица АН является ^-самосопряженным опе-

ратором в пространстве UA- ИЗ доказанного и инвариантности про-

странства U

относительно матрицы / — АН — SL~

вытекает, что

является линейной оболочкой DL'

— ортонормированной си-

стемы собственных векторов %, ..., ^ матрицы s£~\ соответствую-

щих ее собственным числам ц

^ ... ^ ^ < 1 (последнее неравенство

доказано в конце § 9.5), где г = rgS.

Таким образом, для любого ф £ UA выполняется неравенство

(ЛЯф,

ФЬ

> (1 - К) (Ф, Ф)о, (11.24.4)

и, следовательно, матрица ЛЯ является D = X"

— положительно

определенным оператором в пространстве U

Таким образом, согласно

10.11,

если использовать дополнительные

обозначения z

= Sp

и y

= Ар

для выбранных матриц D и Я,

обобщенный метод сопряженных градиентов принимает вид

SttP^sT-^+SZ-

IO^SL-

^-/);

§«*

&*-

> -(1 /7

)

[Si"

5*~

• —

-i

(S«*-'

—§«*-

)];

5»->-(l/

)[(/-sT-»)5*-'-e»_

(6»-«-|»-»)];

6=1;

<?»-i

7ft-i

III*-'II*

*>l;

</ft

Kz-sl-i)!*-

h-г

^ft-l>

^— *>•••> ^8>

(11.24.5)

He*—

I»

a*«

(Sw*

+/),

где Се = L"

—

L^SL"

— самосопряженная и положительно опре-

деленная в пространстве

матрица.

Рассмотрим на примере системы (11.24.1), возникающей при ап-

проксимации кинетического уравнения для сферической геометрии,

407

некоторые вопросы практической реализации предлагаемого метода.

Нетрудно видеть, что поскольку матрица L является блочной нижней

треугольной матрицей с диагональными блоками порядка т, то при

произвольной индикатрисе рассеяния g=g (г, |w

) каждый шаг метода

(11.24.5) требует D (Nm

) арифметических действий. Если же инди-

катриса рассеяния четная по переменной \i

функция, т. е. g (г,

\х

)

== g (г, — (л

), то L = L и, следовательно, каждый шаг процесса

требует только О (Nm) арифметических действий.

Очень важным на практике является случай, когда индикатриса

рассеяния имеет вид

*(м*о)= ijM'M-

(

IL24

В этом случае

*(',

\h)-8(r, —

|*о)

= 2 2 flu-iii»-

, (11.24.7)

где t

= [(t +

1)/2],

и, следовательно, в формуле (9.5.31) ранг мат-

рицы С

— С

= 2 [fx

2£

Q(jt

a£

] ® a

t-i не превосходит величины

. Здесь

1 ... 1

(

1 ... 1

(1L24.8)

—матрица порядка /и, матрица \i введена в§9.5

щ = diag {ац,

...,а/лг},

i = О, £. Нетрудно показать, что для специального вида индикат-

рисы (11.24.8) общее число арифметических действий на итерацию

не превосходит величины О

(Nmt%),

а при неотрицательных коэффи-

циентах

*_1,

i = 1, t

— величины О (Nmt

). При этом общий объем

требуемых ячеек памяти ЭВМ, достаточных для реализации про-

цесса, является величиной

(Nt

Частный случай. Предположим, что индикатриса является

четной функцией по переменной \i

и матрица S положительно полу-

определена в Е

. Тогда матрицы S и S

, где S+ — обобщенная об-

ратная для матрицы S матрица, являются самосопряженными и по-

ложительно определенными операторами в пространстве SE

Выберем Н = L"

и D = S+ и покажем, что матрица АН является

D-самосопряженным и положительно определенным оператором в

пространстве U

= (I — АН) Е

= SL^En = SE

и, следовательно,

для решения системы (11.24.1) применим обобщенный метод сопря-

женных градиентов. Так как для четной по переменной |х

индикат-

рисе

S^S!®

[!!]•

408

то матрица S положительно полуопределена в Е

только тогда когда

«ятпяпя Л поло*™,™ полуопределена в £

. Нетрудао' также

матрица S

положительно

видеть, что

= -Lct®

= -i—51/2

[S+]l/

21/2

-[S+]

Теперь поскольку S

]

= i|) для любого г|? £ SE

, то

(ЛЯф,ф)

= ((/-5£-

)ф, 9b

= ((/-S

L-

Ф)

= (£ (/—S

)9) = (^ ЛЯ

)

(11.24.9)

для любых г|), ф g S£

, где $ =

[S+]

гр, ф = [S+F

ф и Г = / —

51/2^-151/2 — симметричная матрица, чем D-самосопряженность

матрицы АН в пространстве UA доказана. Далее, так как все соб-

ственные числа матрицы S

и L"

S совпадают, и, соглас-

но § 9.5, р (Ь-

8)<. 1, то матрица Т будет положительно определена

в Е

и, следовательно, матрица AL"

будет 5+-положительно опре-

делена в пространстве UA, причем будет выполняться неравенство

(ЛЯф,

)

-р (L"

S)) (Ф,

)

(11.24.10)

Таким образом, для решения системы (11.24.1) применим обоб-

щенный метод сопряженных градиентов с выбранными матрицами

D = S

и Я = L"

. На первый взгляд основную трудность при реа-

лизации формул (11.24.5) составляет участие в вычислении скалярных

произведений матрицы S+, прямое нахождение которой в общем случае

весьма трудоемко. Очень простой эта задача оказывается лишь в слу-

чае изотропного рассеяния, когда g (jx

) = 1/2 (здесь и далее опять

ограничиваемся случаем сферической геометрии). В этом случае

= (AinQ ® 2

)/2, где матрица Q определена в (11.24.8), и нетрудно

видеть, что Sf = 2А

\iQ ® 2

и, следовательно,

S+ =

где

= diag{2

„,

1);

25 =.

-1

о,

если 2

= 0;

если 2

^ 0

Отсюда, используя соотношения

S+^

= 2

I|) = (S

®/N)®/

^; S+SI|)-SS+^ = ^, (11.24.П)

которые выполняются для любого вектора г|)£ UA = S£

, получаем

формулы для вычисления, например, коэффициентов е

и <7&

из

(11.24.5) в следующем виде:

409