Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов
Подождите немного. Документ загружается.


жению
в
§ 10.6, операция
Р
при
а = 1
состоит
в
нахождении реше-
ния задачи (11.6.5), (11.6.6)
при f
x
= с (и^
2
— и§:
w
k
+W = (Q
n
-P
n
c)-iP
n
c(u
k
0
+
V*-uk).
(11.6.7)
Далее полагаем
u*+
l
=u*
+
l
'
2
+
w>
+
U*.
(11.6.8)
За нулевое приближение
и%
— Su°
можно взять решение задачи
(11.6.5)
с f
±
= F при
соответствующих краевых условиях. Между
функциями
и%+
г
и и\
существует соотношение, которое получается,
если
в
равенство (11.6.8) подставить результат операций (11.6.1),
(11.6.7):
и\+^Мси\ + М
х
Р,
(11.6.9)
где операторы
М, М
г
выражаются формулами
М ^{I-Qn
1
Р
п
cyHSLo'-Qn
1
Р
п
)\
M^il-Qn'PnCy^U
1
.
(11.6.10)
Очевидно, что при \\М
с\\
= q<
1
KPi
-метод, определенный фор-
мулами (11.6Л), (11.6.7), (11.6.8), сходится
в
пространстве Ж
со
ско-
ростью —
In
q. Также очевидно,
что
если метод простой итерации схо-
дится
в || ||, то
существуют операторы сходящегося /СР-метода
(на-
пример, таковыми являются операторы
с Р
п
= 0).
Если отойти
от той
общей постановки задачи, которая была изло-
жена,
и
перейти
к
рассмотрению некоторого более узкого класса
за-
дач,
то на
этом классе интерес представляет
Задача А. Найти
вид
дифференциальных операторов
Q
n
, Р
п
и вид
граничных условий (11.6.
6),
чтобы
на заданном
классе
задач,
во-первых,
задача (11.6.5), (11.6.6) была разрешима
и
довольно легко
решалась чис-
ленными методами
и,
во-вторых, \\М
с\\
была достаточно малой вели-
чиной.
Очевидно,
что при
практической реализации
KPi под
операцией
К можно понимать
и
простую итерацию
для
задачи (5.1.2), (5.1.5).
В случае вырожденной индикатрисы рассеяния находят
в
опера-
ции
К
кроме нулевого момента функции
u
k+1
I
2
еще конечное число
не-
которых линейных функционалов
от
u
k+1
/
2
,
вид
которых определяется
слагаемыми индикатрисы рассеяния. Уравнения (11.6.5) следует рас-
сматривать
в
этом случае
как
систему уравнений
для
нахождения
по-
правок
к
этим функционалам
и
нулевому моменту.
Приведем
два
возможных способа построения операторов
Q
n
, Р
п
.
1.
Краевая задача
с
условиями (11.6.6)
для
Р
п
-уравнений метода
сферических гармоник определяет одновременно
с
моментами высших
порядков
от
функции
ф (или и) и
нулевой момент
w =
cp
0
. Алгоритм
нахождения нулевого момента
w = ф
0
из
решения этой задачи назовем
операцией
Р.
Иногда удается более конкретно записать вид уравнения
(11.6.5).
Для
этого исключают, если
это
возможно,
из
Р
п
-уравнений
все моменты ф, кроме w. Для случая постоянных коэффициентов и
/i^O
процесс исключения описан
в
[81, 122].
В
результате получают крае-
360

вую задачу для дифференциального уравнения относительно функ-
ции w. При численной реализации такой операции Р могут возникнуть
трудности, связанные с тем, что выражение Р
п
(f
x
) иногда (например,
в задачах с неизотропным источником или многозонных задачах) яв-
ляется обобщенной функцией, а коэффициенты уравнений могут быть
разрывными функциями. Тогда системы разностных уравнений следует
составлять подобно тому, как это сделано в
[118].
Сначала составляем
для первоначальной системы Р
п
-уравнений, содержащей все моменты
функции, систему разностных уравнений дивергентного типа, а потом
в системе разностных уравнений исключаем все функции, кроме w.
2.
Р
т
-Уравнения (см. гл. 8) могут быть также использованы в
операции Р. Для некоторых задач показано
[120],
что метод сфери-
ческих гармоник не является оптимальной операцией Р, а лучшую
сходимость КР
г
дает операция Р с использованием
P
N{
-уравнений
при специальном выборе коэффициентов.
Далее обозначим Р*(я) операцию P
t
(i = 1, 2, ..., а), которая
заключается в решении уравнения (11.6.5) с дифференциальным опе-
ратором Q
n
2 я-го порядка.
В работе Г. Коппа [296] предложено использовать при решении
уравнения Пайерлса в качестве облегченной краевую задачу для
Pi-уравнения. Итерационная схема метода, который был назван синте-
тическим, иная, нежели для КР±: она определяется формулами
(10.23.2), (10.23.3). Вычислительные схемы обоих методов по-разному
чувствительны к ошибкам округления. Наибольшее различие как
в алгоритмической реализации, так и в обосновании этих методов
проявляется в задачах, в которых операторы определены на классах
функций, удовлетворяющих краевым условиям. Однако очевидна
и общность идей в КРг и синтетическом методе.
§ 11.7. СХОДИМОСТЬ
KPi(n)-METOJX\
Сходимость /СР
х
-метода покажем для самосопряженного кинети-
ческого уравнения (5.1.23). Класс дифференциальных операторов
Q
n
, Р
п
, дающих сходящийся /СР
х
-метод, был описан леммой 1 и за-
дачей А в работе [120] (см. задачу А в § 6). Далее будем использовать
обозначения и результаты § 5.1. Функция и £ Я
0
, реализующая
минимум функционала (5.1.25), является обобщенным решением за-
дачи (5.1.23), и для G
{v)
справедливы неравенства (5.1.26), а опе-
ратор LQ
1
S
0
является вполне непрерывным положительным и само-
сопряженным в #
0
оператором. Поэтому для уравнения (5.1.23)
применимы утверждения, изложенные в § 10.9.
Сходимость TCPi-метода докажем в унитарной норме, порожденной
функционалом G (v). Согласно неравенству (10.9.6) операция К умень-
шает значение функционала G (v).
Пусть операция Р
х
состоит в решении уравнений метода сфери-
ческих гармоник в Р
27г
_
г
приближении с граничными условиями Мар-
шака — Владимирова
[41].
В обозначениях работы [41] эти уравнения
имеют вид _
U")ufi+V*=Sl
0
n
>w
k
+
l
t
2
+Fl
n
\
(11.7.1)
361

где для операции Р
г
Я
п
>= S<
n
>
(u
k
+
1
/
2
— u
k
).
Окончательно
u
k+l
==u
k + l/2
+ w
fi+\/2
m
(11.7.2)
В уравнениях (11.7.1) функция
w
k
+
{
l
2
принадлежит пространству
функций, представимых в виде
6 = 0 /
где функции i|)
2fei
(х) пробегают соболевское пространство Wty (D)
[218],
a F
2
ft,f (О) — сферические функции. Это пространство функций w
обозначим Я'. Тогда (...)* в формуле (11.7.1) означает проектиро-
вание на это пространство. В работе В. С. Владимирова [41] показано,
что функция w £ Н\ реализующая min G (ш), является решением
уравнений (11.7.1) при соответствующей правой части. Следовательно,
/СР
г
метод сходится в Н
0
[124].
Пусть теперь операция Р
х
состоит в решении краевой задачи для
Р^-уравнений, рассмотренной в § 8.4. Пусть Н' — пространство
кусочно-постоянных по Й функций, на котором определены Р^-урав-
нения. В § 8.4 показано, что решение
Р
17
-уравнений реализует
min G (v). Следовательно, если за операцию Р
г
взять решение крае-
вая'
вой задачи для Рц-уравнений, то такой /СР
г
метод сходится в Н
0
[124].
Заметим, что в обоих методах ускорения сходимости поправка
до*н-1/2
не
удовлетворяет точно краевым условиям: она не лежит в об-
ласти определения оператора L
0
, однако лежит в области определения
обобщенных операторов задачи.
§ 11.8. ЦИКЛИЧЕСКИЙ ЯР1(0)-МЕТОД
Рассмотрим краевую задачу (5.1.23). За операторы В
ъ
С
19
т
х
в формулах (10.6.5) возьмем простейшие операторы В
х
= /; С
г
=
— а
7
-7; т
г
= /, где а; — циклически -меняющийся относительно k
числовой параметр. Пусть N — период его изменения. Тогда после
операции К полагаем
где k = 0, 1, ..., aj
+
N = а/. В этом случае Р
г
(0) является довольно
простой операцией в пространстве функций, представимых в виде
S
0
u. Пусть
E
k
= U
0
--
U^
=
^ZiSoV
h
где v
k
— собственные функции задачи (5.1.27), соответствующие
собственным значениям Я/ > 0 (обозначим 7; =
^у"
1
).
Тогда после N
362
(11.8.1)

итераций
E
k
+
N
^M
i
ztS
0
v
i
,
(П.8.2)
—
— **
где величины M
t
определяются формулой
M
t
=
П (y
t
—
о/)/
(1 —
о,).
Пусть
TN(X)
—
многочлен Чебышева JV-й степени
на
[—1,1],
а
Р
7
-,
/=1,2,
...,
N, — упорядоченные перестановкой
Хдг
корни
многочлена. Тогда если взять а,-
=
0 (Ру
+
1)/2,
где 0 =
=gll— ехр
(—dao"
1
)]
<1; g"=sup vrai |cS|g||; d—диаметр области/), a
величина а
0
определена
в §
5.1.
и
считать,
что
величина 0 довольно точ-
но оценивает границу интервала,
в
котором находятся значения
у
к
,
то
после N итераций
\M
t
\
<
0N
=
|7V/
(20"
1
— 1) |
_1
<
1
и, следовательно,
К+^]<6^И].
Здесь АЦ
-■=
О (N).
За а
7
-
можно взять числа, полученные
из
Г-по-
следовательности (см.
§
11.18).
§ 11.9. /СЛМ-МЕТОД ДЛЯ ПЕРИОДИЧЕСКОЙ ЗАДАЧИ
Оценим скорость сходимости различных вариантов /СЯ-метода
для
задачи (11.1.4)
с
постоянными коэффициентами. Некоторые изложен-
ные результаты непосредственно обобщаются
на
2я7
1
-периодические
задачи
с
переменной функцией
с
[120, 121]. Начнем
с
исследования
KPi{n)-метода,
в
котором операция
Р
х
(п) сконструирована следую-
щим образом. Пусть Q
n
(t),
Р
т
(t)
—
многочлены вида
п
т
Qn(t)=
2
W
2
*; P
m
(t)=
2
p
mkt
2k
, (И.9.1)
где
р
т0
= 1,
п
> т,
удовлетворяющие при — оо
< /<
оо условиям
Pm
(t)
>
0; Q
n
(0
-
сР
т
(t)
>
0. (11.9.2)
Пусть
X =
i/A
1
/
2
,
где
Д
—
оператор Лапласа. Операцию
Р
г
(п)
определим как операцию по нахождению 2 я-периодического решения
уравнения
Q
n
(Z)^+^ = P
m
(X)(cw^+^ +
f^
(И.9.3)
где
fi = с
(иЬ+
х
1
2
—
и%).
После выполнения ее полагаем
tt
g+l
=
a{+l/2
+ a
,ft+l/2
e
(11.9.4)
Оценим в пространстве
m
скорость убывания ошибок. Пусть
^+i/2
=
2^
+1/2
exp(ijx). (11.9.5)
Подставляя
в
(11.9.3)
это
выражение
и
заменяя
f
x
выражением
2c[crj — 1]
е/
ехр (/jx), получаем
t^+^^WntM-^m^cr^m^ClCr^-lle}, (11.9.6)
363

где Я/ =
/|j|.
Для ошибок 8^
+1
= е^+~/
2
+ w^
+l/2
справедливы
рекуррентные соотношения
е5
+1
= г|)(^)се/, (11.9.7)
где функция i|) имеет вид
* (0 = *
W.
^ W,
Pm
(0, d = [l - с Р
т
(Wnit))-
1
lr(() -
- PmWQn (t)l (П.9.8)
Следовательно, если обозначить
11*|1
= 11*|1№п,Рп^) = тах|ф(0|, (И.9.9)
то
||е*+Ч|<с||*||||е*||. (11.9.10)
Справедлива
Лемма
11.9.1.
Если
многочлены
Q
n
(t), Р
т
(t) удовлетворяют
условиям
(11.9.1),
(11.9.2) и
Pmd)/Qn(t)
< U+r(t)] (1 +
С)"
1
,
(П.9.11)
то
HUQn,
Р«,с)<1.
(11.9.12)
Доказательство состоит в установлении при выполнении условий
леммы справедливости неравенства |г|)| < 1. Лемма 11.9.1 останется
справедливой, если в (11.9.11), (11.9.12) заменить знак < знаком <.
Расчеты показали, что
||i|)||
< 0,225 при
Q
1
(t)
=
1
+
q
n
t
2
;
P
0
(t) =
= 1; ^ii =1/3
и0<с<1.
Это значит, что для любых п > 0,
т > 0 (п > т) существуют Q
n
, Р
т
, для которых
||г|)||
< 1. Пусть
£nm(c) = inf
|| "ф f(
(Qn, Рту с) — наилучшее приближение нуля на
р
т><>т
классе многочленов Q
n
, Р
т
вида (11.9.1), (11.9.2). Тогда
Епт (с)
< 0,225 при п > 1, т>0, 0<с< 1. (11.9.13)
Лемма 11.9.2.
Справедливы неравенства
Е
ы
(с)^Е
пт
(с) при £>л, i>m; (11.9.14)
£пт(сК^птй ПРИ 0 < с' < С. (11.9.15)
Доказательство (11.9.14)
очевидно.
Неравенство (11.9.15)
доказывается цепочкой неравенств Е
пт
(с)
> max |г|э(t,
Qn,
Рту
с')
|
>
^ Е
пт
(с'), где (?„ (t), Р
т
(f) —
те многочлены, на которых дости-
гается Е
пт
(с).
Из рассуждений этого параграфа вытекает
Теорема
11.9.1.
Если в КР\(п)-методе для
2п-периодической
задачи операция
Р
х
(п) состоит
в решении
уравнения
(11.9.3),
в ко-
тором
многочлены
Q
n
(t),
Р
т
(t)
удовлетворяют
требованиям
(11.9.1),
(11.9.2)
и
леммы
11.9.1.
а0<с< 1, то КР
г
(п)-метод
схо-
дится
в
пространстве
tn и
l|e*ll<[c||iHI(Q
n
,^m^)]Mle
e
l|. (11.9.16)
где е° —
ошибка начального
приближения,
а |№|< 1.
364

Нетрудно убедиться
в том, что
оценка (11.9.16)
для
величины
||
e
k
|
достигается,
а
следовательно,
ее
нельзя улучшить.
Лемма 11,9.3. Если полиномы
Q
n
, Р
т
удовлетворяют условиям
(11.9.1),
(11.9.2)
и Q
n
(0) = Р
т
(0), то
КР
г
(п)-метод сохраняет
на каждой итераций
при k > 0
общий баланс нейтронов.
Доказательство.
Из
условий леммы 11.9.3 получаем,
что <7по
=
1
•
Проводя полную итерацию
по
/СР^-методу,
на-
ходим,
что
J/J+
1
—
коэффициент
при
нулевой гармонике функции
u
k+\
— всегда удовлетворяет
при q
n0
= 1
уравнению
u%f
x
= (1 —
—
с)"
1
Л>о>
£ = 0, 1, ..., а это ц
есть уравнение баланса нейтронов.
Из леммы 11.9.3 следует, что
для
получения «балансного» прибли-
жения решения задачи достаточно лишь последнюю итерацию про-
вести
с
многочленами
Q
n
, P
m
,
удовлетворяющими условиям леммы
11.9.3,
а все
предыдущие итерации выполнять
с Q
n
, P
m
,
дающими
большую сходимость итераций. Балансные
и
небалансные схемы
/СР-метода будем обозначать соответственно через
БКР и
НБКР.
§ 11.10. ВЫБОР ПАРАМЕТРОВ ОПЕРАЦИИ Р И ОЦЕНКА ||ф||
Эффективность операции
Р
зависит
от
выбора параметров
q
nk
,
Pmh,
определяющих
эту
операцию
[120].
Очевидно,
что
операция
Р
будет наиболее эффективной
в
пространстве
nt,
если
H>|(Qn,
Рт,
С)
=
Е
пт
(с).
(11.10.1)
Решение задачи (11.10.1)
по
нахождению многочленов
Q°
n
(t),
Р°
т
(t)
может быть получено нелинейном методом последовательных прибли-
жений, основанным
на
чебышевском альтернансе.
В качестве меры эффективности можно взять величину квадратич-
ного функционала
J(Qn,P
m
,c) = ]r(t)p(t)dt
(11.10.2)
о
[где p(t)
—
некоторая неотрицательная функция]
и
решить задачу
о минимизации функционала
J.
Значения
p
mky
q
nk
,
минимизирующие У,
будут оптимальными, если рассматривать сходимость итераций
в не-
которых других функциональных пространствах.
В
этом случае
па-
раметры удовлетворяют системе трансцендентных уравнений
_*L.
=
0;
-*L =
0; £=1,2,...,
m; t-0,
1,...,
п.
(11.10.3)
dpmk dq
ni
При
m = 0, n
—
1, c=l
значение
для q
n
находится
из
(11.10.3)
в
явном виде:
•„
l
_rJj=iffl.
r
(op
W
*l"
,
?[-
L
7
ffl
-]'p«'«- <"-
1М
>
*-о
^ о
В табл. 11.1 приведены результаты расчета БКР при
с =
1;
Р
0
= 1;
Qi
= W
2
+
1;
в
табл. "11.2 —
при
Q
x
= q
n
f + q
10
; Р
х
*=
p
n
t
2
+ 1;
365
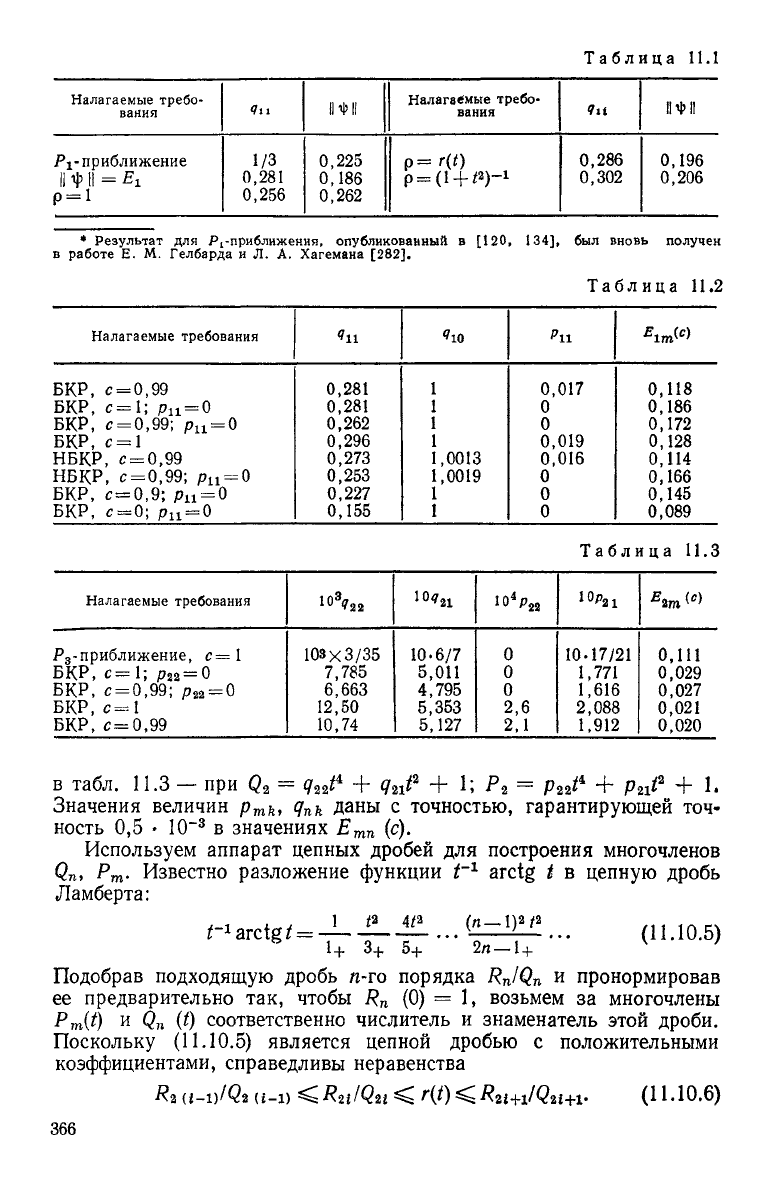
Таблица 11.1
Налагаемые требо-
вания
<7п
ИИ
Налагаемые требо-
вания
<7it
ШИ
Р
г
- приближение
II
*
II
= Ei
р
=
1
1/3
0,281
0,256
0,225
0,186
0,262
р=г(0
р = (
1
+ /2)
-1
0,286
0,302
0,196
0,206
* Результат для Р^приближения, опубликованный в [120, 134], был вновь получен
в работе Е. М. Гелбарда и Л. А. Хагемана
[282].
Таблица 11.2
Налагаемые требования
Hi
Но
*im«>
БКР, с
= 0,99
БКР,
с=1; рц = 0
БКР, с
= 0,99; р
п
= 0
БКР, с
=
1
НБКР,
с
= 0,99
НБКР, с = 0,99; р
п
=
БКР,
с = 0,9; рп = 0
БКР, с
= 0; рц = 0
= 0
0,281
0,281
0,262
0,296
0,273
0,253
0,227
0,155
1
1
1
1
1,0013
1,0019
1
1
0,017
0
0
0,019
0,016
0
0
0
0,118
0,186
0,172
0,128
0,114
0,166
0,145
0,089
Таблица 11.3
Налагаемые требования
103
*22
Ю<7
2
^22
Юр,
'21 ^2т
(С)
Рд-приближение, с= 1
БКР,
с=1; /?22 = 0
БКР,
с = 0,99;
р
2
2
= 0
БКР,
с=г-1
БКР,
с = 0,99
103x3/35
7,785
6,663
12,50
10,74
10-6/7
5,011
4,795
5,353
5,127
0
0
0
2,6
2,1
10-17/21
1,771
1,616
2,088
1,912
0,111
0,029
0,027
0,021
0,020
в табл. 11.3 — при
Q
2
=
?22*
4
+
<72i*
a
+ 1; Р
а
=
Р22*
4
+
Рп*
2
+ Ь
Значения величин
p
mky
q
nk
даны
с
точностью, гарантирующей точ-
ность
0,5
■
10"
8
в
значениях
Е
тп
(с).
Используем аппарат цепных дробей
для
построения многочленов
Q
n
,
Р
т
.
Известно разложение функции
t'
1
arctg
t в
цепную дробь
Ламберта:
t~
x
arctg /
=
I4.
3-j. 5+
(/I — 1)2/2
(11.10.5)
2л —1 +
Подобрав подходящую дробь
я-го
порядка R
n
IQ
n
и
пронормировав
ее предварительно
так,
чтобы
R
n
(0) = 1,
возьмем
за
многочлены
P
m
(t)
и Q
n
(t)
соответственно числитель
и
знаменатель этой дроби.
Поскольку (11.10.5) является цепной дробью
с
положительными
коэффициентами, справедливы неравенства
R*u-i)IQtti-i)<Ru/Qu<r(t)^R
u
+i/Qu+i-
(П.10.6)
366

Можно убедиться в том,
что
#n>0;
Q
n
>0 nO<R
n
/Q
n
<l
(11.10.7)
при действительных
t, что при
четном
п
степень многочлена
Q
n
рав-
на
2 л, а
степень многочлена
R
n
(t)
равна
2
(/г — 1);
при
нечетном
п
степень многочленов Q
n
(t)
и R
n
(t)
равна
2 п, а
при
с £ [0,
1],
п = 2*
многочлены
P
n
_
x
=
i?
n
, Q
n
удовлетворяют условиям (11.9.1), (11.9.2).
Для построения операции
Р
следует взять многочлены
Р
п
„
ъ
Q
n
толь-
ко
при
четных значениях
п\
основанием
для
такого выбора служат
рассуждения
в §
9.10, неравенство (11.10.6)
и
Лемма. 11.10.1.
||ф|| (Q
2b
R
2
u
1)<с
0
Г\
где Q
2i
, R
2i
—под-
ходящие многочлены цепной
дроби (11.10.5)
21-го
порядка,
а с
0
— по-
стоянная,
не
зависящая
от i.
Вспоминая связь между ортогональными многочленами
и
цепными
дробями
[210],
мы видим,
что
многочлен
fl Q
2j
(it
1
) с
точностью
до
постоянного множителя совпадает
с
многочленом Лежандра
2/-й
степени.
Покажем,
что в
случае периодической задачи операция
Р
[Q„(^-cP
n
.
1
2)]t»*+»/a
=
P
Il
.
1
(ig)c(ii5+«/2-ii») (11.10.8)
с выбранными
в
данном параграфе многочленами сведется
к
п-крат-
ному решению периодических задач
для
эллиптических уравнений
2-го порядка.
Для
этого многочлен
Q
n
—
с Р
п
_
г
разложим
на
мно-
жители
Qn
(t)-cP
n
„
1
(t)
=
b
n
fl
(<"
+
тД),
(11.10.9)
где
b
n
—
коэффициент при
f
n
многочлена Q
n
(t), а
тД
=
ф/~
2
,
ф
2
—
корни уравнения (9.11.7) для
п = М. Из
неравенств (9.11.8) заклю-
чаем,
что тД > 1 при i = 1, 2, ..., п—\ и 0 <
T^i
< \in\
Поскольку
все
корни уравнения
Qn
(it) = 0
(11.10.10)
действительны
и по
модулю больше единицы
[ибо они
обратны
\i
k
(k
= 1, 2, ..., /г,
\ik
<
pift+i) — положительным корням много-
члена Лежандра],
а
корни многочлена
P
n-1
(i, t)
лежат между кор-
нями уравнения (11.10.10)
(см.
[121],
заключаем,
что
многочлен
^п-1
(0
представим
в
виде
Pn-l(Q
=
*n nV +
lft),
(11.10.11)
где
т/2 > 1, а ^
— коэффициент
при
Z
2
("-i),
и что
[if
+
2
i
< тД
4*2
< ^Г
2
, / = 1, 2, ..,, п
—
1, а
следовательно,
т?
2
/тЛ
=
1
+
0(/1-1), t
=
l,2,...,
/i—l. (11.10.12)
Переписав уравнение (11.10.8)
в
виде
6n
fl (-/
2
A +
T?0^+i/
2
= d/n (-/
2
A +
T?
2
)C(^+I/2-^),
(11.10.13)
367

видим,
что
решение этого уравнения сводится
к
последовательному
нахождению решений периодических задан
(
_
/
2
A
+ T
2
l)2
j
==
^
(
^+i/2_^
);
(Ц.10.14)
(_/2
Д + т
2)^
1==(т
2
2
_
Т
2
)
^
1
. 1 (ПД0.15)
г?
=
г*-х
+
х#-и
t=l,2,..., л—1,
j
В результате получим,
что w
k
+V
2
=
Zn-\.
В
силу соотношения
(11.10.12) процесс нахождения г?,
i =
1, 2, ..., п — 1,
устойчив
по п.
Таким образом, имеет место следующая ситуация: скорость схо-
димости
КРг
(п)-метода
растет
с
ростом
п
как In я,
а
трудоемкость
операции
Р
г
(п) при
этом увеличивается.
В
работах [119—121,
127]
на модельных задачах исследованы оптимальные
с
точки зрения
об-
щей затраты числа арифметических действий алгоритмы К Pi (п)-
метода, названные дешевыми
по
цене
Ц (KPi
(п))
алгоритмами;
для
них показана асимптотика роста п (е)
при
е
->■
0,
где е
— точность
решения задачи.
В следующих параграфах мы рассмотрим различные модификации
/СР-метода
для 2
я-периодической задачи.
Для
этого введем некоторые
единые обозначения:
Q
n
и
Р
т
—
многочлены, удовлетворяющие
ус-
ловиям (11.9.1), (11.9.2); TN
(Х)
—
многочлен Чебышева первого
рода
для [—1, 1]
степени
N,
рь
=
cos
(2k
— 1) n/2N; 9
N
=
| T
N
(б) Г
1
;
X = / i
A
1
/
2
,
(11.10.16)
где величина
б
определяется по-своему
в
каждом конкретном случае;
предполагается,
что
|
б
|
>
1
при 0
^
с
<
1.
§
11.11.
KPi(n)P
2
(0)-METOH
Рассмотрим /СР-метод
при
а =
2,
в
котором
за
операции
Р
ъ
Р
2
возьмем операции
Р^п),
Р
2
(0). Пусть
Р
г
(п)
имеет
вид
Q^^)^
+1/3
==^m(^)^
+1/3
+
^(«J
+1/3
-^)];
где
u
k
+
x
l
z
является результатом выполнения операции
/С.
Пусть
операция
Р
2
(0)
выполняется
при В
2
= /,
С
2
=
а
к
с /, т
2
==
/:
^
+
2/3
=
(1_
алС
)-1
адС
(^+2/3_^)
;
W
J+l
=
=
W
J +
2/3_f.^
+
2/3
#
(11.11.2)
Тогда после полного цикла
из N
итераций
4
+N
=
П
(^(/|п|)-а
;
)(^-а^8
п
\
368
(11.11.1)

Пусть т = min я|з (/1 и
|);
М = max \|) (/1
п
|) < (Г
1
, а об ошибке на-
п п
чального приближения е° известно только, что | ей | ограничены не-
которой постоянной с
0
. Для максимального уменьшения всех | е* |
за N итераций необходимо взять aj из множества чисел
(М + т + (М — т) p
fc
)/2
f
k = 1,
2„...,
N. (11.11.3)
Тогда
|в£
+АГ
|<е*|в2|;
6 = (2c-
1
-M-m)/(iH-m). (11.11.4)
В частности, а
2
= (М +
т)12
при
JV
= 1. Ясно, что чем больше
| б |, тем быстрее сходится КР
г
(п) Р
2
(0). Поэтому интересно найти
такие коэффициенты уравнения (11.11.1), которые давали бы наиболь-
шую величину
|
б
|
при заданном значении я. Можно показать, что для
п = 1 оптимальным в этом смысле является Pi-приближение метода
сферических гармоник (Р
0
s
U Чп
= 1/3): для него
|
б
|
^ 8,88 с
-1
— 1,
т. е. е
х
< с/ (8,88 — с)< 0,127 с.
Если за Q
n
(/),
P
n
„x
(*) взять многочлены, определенные леммой
11.10.1,
а величину М для этих многочленов обозначить М
п
(6<.
< М
п
< 1) и учесть, что для них т = 0, то при N = 1 имеем
|б|
> 2 с'
1
Мп
1
— 1, т. е. 0
Х
< М
п
с/(2 — М
п
с)< М
п
с. Например,
для п = 2 0
1
<с/(18 —с).
За а/ можно взять числа, образованные из Г-последовательности.
§ 11.12. Я
2
Р-МЕТОД
В § 11.10 изложены алгоритмы построения многочленов
Q
n
(0>
P
n
-i(f),
для которых
|[ф||
(Q
n
, Р
п-1
,1)=0
(л""
1
).
Указанный порядок ма-
лости
||ip||
нельзя улучшить. Объясняется это тем, что величины г (t) и
Qn
1
(t) P
n
-i (О
с
разной скоростью убывают при t ->оо [как О (tf"
1
)
и О
(t~
2
)
соответственно], что приводит к различным асимптотическим
поведениям собственных значений операторов операций К и Р. Для
ускорения сходимости итераций можно предложить такой вариант
метода: за один итерационный шаг выполнять две операции К и опе-
рацию Р. Тогда собственные числа операций /С
2
и Р будут убывать
асимптотически одинаково [как О
(Я„
2
)],
и поэтому можно надеяться
при разумном выборе многочленов Q
n
(t), Р
п
_
г
(t) на более быстрое
убывание ошибки К*Р
г
(п) за один итерационный цикл. Если же ока-
жется, что сходимость одной итерации К
2
Р± (п) сравнима со сходи-
мостью пары итераций КР
г
(л), то К
2
Р\ (п) будет предпочтительнее.
Схема /C
2
^i (
п
) имеет вид:
U'+W^SLQ^CUI
+ F); ^
+2/3
= SLo
1
(^J
+1/3
+
^);
]
Q^^)^
+2/3
= ^n-i(^)(c
2
^
+2/3
+ c
2
(^
+2/3
-^)); (1Ы2.1)
ui+
l
=u*+w+
&+***;
)
где Q
n
(/), P
n
_
x
(t) — многочлены вида (11.9.1) и Q
n
(t) —
c
2
P
n
^
±
(t) >
>0.
Тогда
е
£
+1
==Ы'М)с
2
е;
369
