Малыхин В.И. Математика в экономике

Подождите немного. Документ загружается.

Для

нахождения предела

«в»

используем

второй

замечательный

предел.

Имеем:

((*

а)/(х

д))*

((1

2в/(х

а)У

((I

2а/(х

д))«*-«>/<*<>

•*•

1/2)за

(

Значит, искомый предел равен:

Нт

(1 +

1Д)<*

№

еЧ

£->«>

Доказать,

что

lim

sin

x.не

существует.

*-><»•

Доказать,

что в

любой точке

области

определения:

lim cos x

cos a;

lim

tg x - tg а; в)

я";

Urn

;

*-*«

*-4fl

X->fl

X-»fl

Д)

lim

.Y->a

Указание.

случае

«а»

используйте

формулу

cos (х

я)

- cos

л;

• cos д — sin x • sin

и;

остальных

случаях

используйте

соответству-

ющие

формулы.

5. На

основании свойств пределов сделайте вывод

существо-

вании

пределов:

а) lim (x +

1)/х;

б) lim

((2x

+ x +

I)/*

);

•

Jf->

«>

X~>

в)lim

(x-cos*);

г) lim

(x/cosx);

д) lim

(cos

л/х).

*-»0

jc->0

*->0

период расцвета финансовых пирамид

России

(1993-

1994гг.)

приемном пункте концерна

«Тибет»

висело объявление

приеме

денег

на 3

мес.

под

100%

(не

годовых,

а за 3

мес.,

т.е.

за 3

мес.

было

обещано двукратное увеличение вложенной

суммы!),

а на

мень-

ший

срок

процентная

ставка была пропорционально меньше, т.е.

на

1,5

мес.

—

50%,

на 3

недели

—

25%

т.д.

Отсюда

выходило,

что

если

положить

деньги

на 3

недели,

после

того

как

срок пройдет,

деньги

изъять

и тут же

снова

вложить,

т.д.»

то за 3

мес. сумма

увеличится

(1 +

0,25)

2,44

раза.

если

операцию

снятия вклада

повторять

еженедельно,

то за 3

мес, сумма увеличится

в (1 +

0,0875)

да

2,71.

это

намного больше,

чем

если положить

на 3

мес.!

Каков

макси-

мальный

коэффициент увеличения

за 3

мес.?

(Это если

начисление

процентов,

снятие денег

опять вложение

их

происходило

бы не-

прерывно

мгновенно.)

4.4.

НЕПРЕРЫВНОСТЬ

ФУНКЦИИ

реальности

имеет

место следующее

обстоятельство;

если

па-

раметры,

характеризующие

ситуацию,

немного

изменятся,

то

немно-

го

изменится

и сама

ситуация.

Здесь

важно

не

то, что

ситуация

из-

менится,

а то, что она

изменится

немного.

Определение

непрерывности

функции.

Точки

разрыва.

Функция

АХ)

называется непрерывной

точке

а,

если

она

определена

некоторой

окрестности этой точки

Дх)

=f(a).

х-*а

Функция

у -

J(x)

называется непрерывной слева (справа)

точ-

ке

и,

если

Дж)=Лв)<

АХ)

а))-

Заметим,

что

при

этом

х-*а-0

*-»в+0

функция

должна быть определена

некоторой окрестности слева

(справа)

от

точки

а.

Заметим также,

что

непрерывность функции

точке

равносильна

непрерывности

ее

этой точке

слева

справа.'

Функция

называется

непрерывной

на

интервале,

если

она

непре-

рывна

каждой

точке этого интервала; непрерывной

на

отрезке

[а,

Ь],

если

она

непрерывна

на

интервале

(а,

Ь),

непрерывна справа

точке

непрерывна

слева

точке

а (а <

Ь).

пмт

Приме

!•

Следующие функции непрерывны

на

всей

числовой

оси:

пп£^

ННаЯ

С;

линейная

cos x, sin

:t;

степенная

jf,

показательная

a > 0

(CM.

раздел

4.3).

IOTP

И)

КОТ

°РЫХ

функция

не

является

непрерывной,

называ-

тся

точками разрыва. Если функция

точке

имеет конечный

ЛУНИ

двуст

°Р°

нни

предел),

но

этот

предел отличен

от

значения

(ЬункГ

ИИ

ЭТ

ЧКе

ИЛИ

точка

не

BX0

область определения

ФУНКПИ

ЧКа

Назьша

ется

устранимой точкой разрыва. Если

не

сппп

Ке

Имеет

конечны

односторонние

пределы,

но

они

вается

адают

(тогда

Двусторонний

предел

не

существует),

то b

назы-

хотя

fai°

4mt

разрша

]

го

Р°

да

Ес

ли

функция

точке

с не

имеет

пялт™

одно

[°

конечного одностороннего предела,

то

точка

назы-

вается

точкой

разрыва

2-го

рода.

У*(

MCp

Точка

являег

гся

устранимой

точкой

разрыва

функции

х)/

так

как

функция имеет двусторонний предел

(sin

x)/x

но

она

не

определена

точке

***

Ример

3. Для

функции

«знак

(сигнум)*

-1

при

х <

О,

.У-здп*^

г^ия-0,

прих>0

ЧКЙ

ЯВЛЯется

точк

°й

Разрыва

1-го

рода,

так как

lim

sgn

-1,

"т

sgn^^!

х->+о

°оа

односторонних предела существуют,

но они не

равны.

^римев

4т

так

кп,,

;

являе

тся

точкой

разрыва

2-го

рода

функции

1/х,

«JUB

1Д

-оо„

Ит

1Д=00]

л-»+0

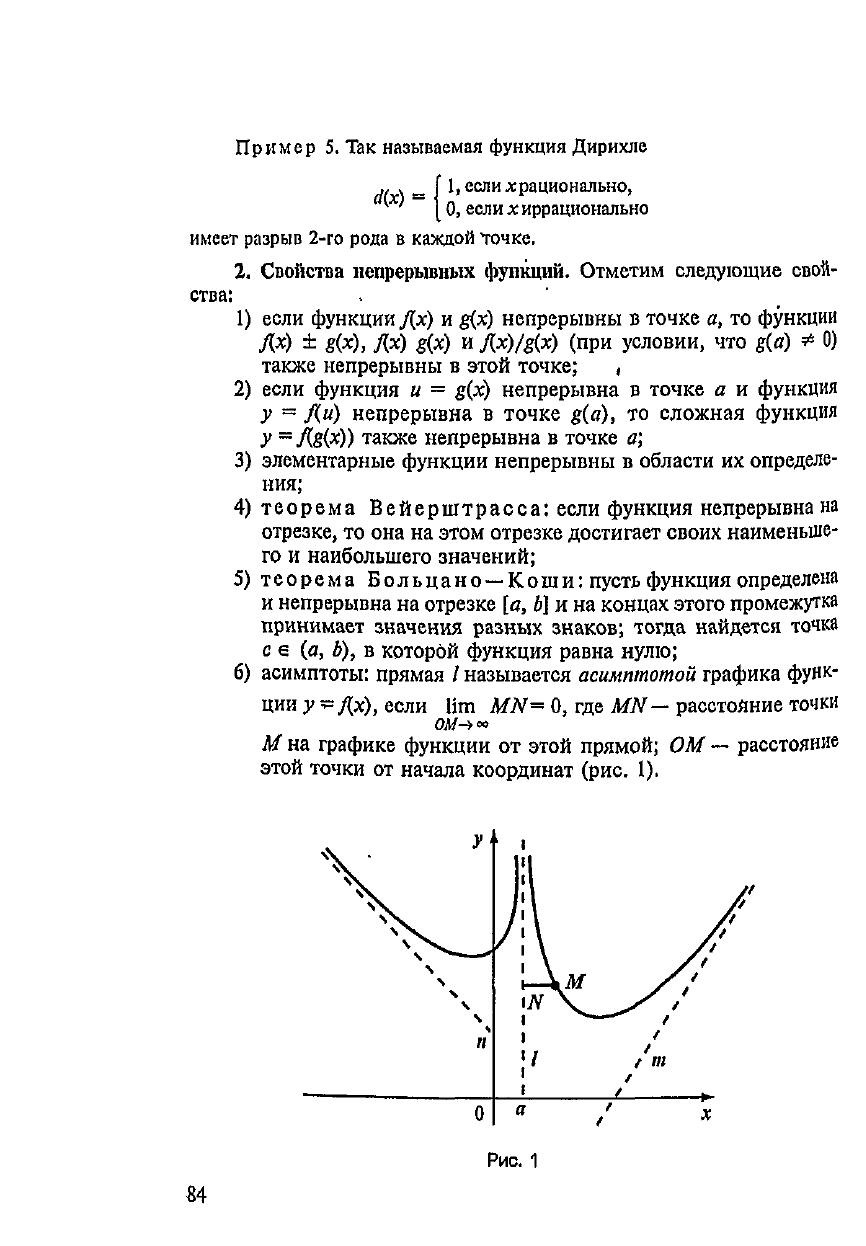
Рис.

Пример

5. Так

называемая

функция

Дирихле

н(

1»

если

«рационально,

[0,

если

иррационально

имеет

разрыв

2-го

рода

каждой

"точке.

Свойства

непрерывных

функций.

Отметим

следующие

свой-

ства;

если функции

Л*)

g(x)

непрерывны

точке

а,

то

функции

Л*)

g(x),

Ax)

g(x)

J{x)/g(x)

(при

условии,

что

g(a)

также

непрерывны

этой точке;

если функция

g(x) непрерывна

точке

а и

функция

f(u)

непрерывна

точке

g(a),

то

сложная

функция

Л#(*))

также непрерывна

точке

а;

элементарные функции непрерывны

области

их

определе-

ния;

теорема

Вейерштрасса:

если функция непрерывна

на

отрезке,

то она на

этом отрезке достигает своих наименьше-

го и

наибольшего значений;

теорема Больцано

—Коши;

пусть

функция

определена

непрерывна

на

отрезке

[а,

Ь]

и на

концах

этого

промежутка

принимает значения

разных

знаков;

тогда

найдется

точка

(а,

6),

которйй

функция равна нулю;

асимптоты: прямая

называется асимптотой графика

функ-

ции

у-

fix),

если

Urn

MN=

0, где

MN—

расстояние

точки

од/->«

на

графике функции

от

этой прямой;

ОМ —

расстояние

этой точки

от

начала координат (рис.

1).

Однако

цах

Р°межутков

она

разрывна

разрывы

эти

1-го

рода.

Рерывной

ВеЛИЧИНа

ПОДОХ

°Д

НОГО

налога

(Р

ис

в)

является

не-

кает

что

функцией

годового

дохода

Отсюда,

частности,

выте-

Но

то и п

Годовые

Д°

°Ды

двух людей отличаются незначитель-

Должны

ЛИЧИЯ

величинах

подоходного

налога,

которые

они

это

обстоят

аТИТЬ)

ТаКЖС

Не

должны

быть

большие. Интересно,

что

Ка

совешп

ЛЬСТВ

Восп

иним

ается

огромным большинством людей

Ют

ся

Вот

еНН

°-

естественн

ое,

над

которым

они

даже

не

задумыва-

Результатне

ЛИ

ЭТ

было

не

так

Когда

это

не

так

КОГДа

непрерывно

зависит

от

начальных данных,

от

парамет-

Асимптоты

бывают вертикальными

наклонными.

Если

Ит

\/(х)\

х-*а

оо

}

то

график функции имеет вертикальную асимптоту (прямая

на

рис.

уравнение которой

а),

Для

наклонной асимптоты условие

ОМ

-»

°°

можно заменить

условием

оо

или х

-оо.

первом случае наклонная асимптота

называется

правосторонней (прямая

т на

рис.

1), а во

втором

слу-

чае

—

левосторонней

(прямая

п ).

Частным

случаем наклонных асимптот являются горизонталь-

ные

асимптоты.

заключение

отметим,

что

непрерывность элементарных функ-

ций

области определения используется

для

нахождения пределов.

Ведь

если

функция

Дя)

непрерывна

точке

а,

то

lim

Л*)

М.

Х-*а

Экономическая

интерпретация

непрерывности. Большинство

Функций,

используемых

экономике, являются непрерывными

и это

позволяет

высказывать вполне значимые утверждения экономичес-

кого

содержания.

Налоговая ставка

имеет примерно такой график,

как на

рис.

а.

ров,

характеризующих задачу

(ситуацию),

то

такая задача

(ситуация)

называется

некорректной,

2. По

своему смыслу такие

функции,

как

функция спроса

D(p),

функция

предложения

S =

S(p),

непрерывно зависят

от р.

Значит,

при

малых колебаниях

цен

спрос

предложения также изменяются

незначительно.

При

более

глубоком анализе обнаруживаются,

одна-

ко,

чисто психологические причины,

по

которым спрос, например,

можбт

измениться скачкообразно. Например,

так

бывает

при

«про-

битии»

круглой

цены.

Цена

растет, растет,

но

люди терпят

спрос

уменьшается

незначительно,

И вот

цена

замерла

около

круглой

ци-

фры. Когда цена, наконец, превысит

эту

круглую цифру, может

про-

изойти

скачкообразное уменьшение спроса.

Это

хорошо знают

фи-

нансисты,

работающие

на

валютных

других финансовых

рынках.

3. При

нахождении рыночной цены облигации (см.

п.

раз-

дел^!)

мы

фактически вывели формулу

Np(№

r)/(\№r),

N—

номинал облигации,

р —

ставка процента,

—

темп

инфляции.

При

выводе

мы

дисконтировали

сегодняшнему моменту бесконеч-

ный

ряд

платежей

будущем.

Тем не

менее

по

формуле видно,

что S

есть элементарная функция

от

ставки процента

р и,

значит,

непре-

рывно

зависит

от

нее. Поэтому

при

малом изменении ставки про-

цента

рыночная цена облигации изменится также мало.

ЗАДАЧИ

На

языке

«£

— 8»

доказать непрерывность функции

\х[

Решение,

Если

бы эта

функция была элементарной,

то

можно

было

бы

просто сослаться

на

общее

положение

непрерывности

элементарных

функций (см,

п. 2

раздела 4.2). Однако

эта

функция

не

является

элементарной, поэтому

ее

непрерывность нужно

специаль-

но

доказывать. Заметим,

что у =

(""*>

при

°'

Пусть

Суще-

(

прих>0.

ствует окрестность

точки'а,

не

содержащая

0, на

которой исследуе-

мая

функция совпадает

элементарной

функцией

(у - х

или

-*)•

Значит,

любой

точке,

отличной

от

нуля,

исследуемая функция

не-

прерывна.

Поэтому нужно

доказать

только

ее

непрерывность

точ-

ке

0. Для

каждого

е > 0

нужно найти такое

§ > 0, что как

только

\х\

то \у\ <

е.'Но

для

этого

достаточно взять

е - 5.

Пусть

Е(х)

—

функция «целая часть

х»,

F(x)

—

функция

«дробная

часть

х».

Нарисуйте графики этих функций, выясните,

в ка-

ких

точках

эти

функции разрывны,

определите характер разрывов.

Решение. Графики обеих функций приведены

на

рис,

Из

графиков

видно,

что

функция

Е(х)

непрерывна

справа

каж-

дой

точке,

в том

числе

целой

л, где

функция равна

п. В то же

время

Тема

ПРОИЗВОДНАЯ

ДИФФЕРЕНЦИАЛ,

ПРЕДЕЛЬНЫЕ

ВЕЛИЧИНЫ

ЭКОНОМИКЕ

5.1.

ПРОИЗВОДНАЯ

ФУНКЦИИ

Определение

производной функции,

се

физический

геометри-

ческий

смысл

Пусть дана функция

Л*)-

Фиксируем произвольную

снкухиз

области определения

£(/)

функцииЛ*)-

Пусть*'-

другая

чка

из

/)(/),

тогда разность

л*'

- х

называется

приращением

аргумен-

та*

обозначается

Дх,

разность значений функции

Л*')

-Л*)

на-

"яется

приращением

функции

обозначается

ДДх).

•

шенм

3е0|Э

ОЙ

ФУ

11К

ии

У~Ах)ъ

точке

называется предел отно-

пои

ее

ри

ац

ния

ДЛх)

этой

точке

приращению аргумента

Дх

/М

если

этот

существует).

Производная

обозначается

)

или/

(х).

Процесс нахождения производной называется

диффе-

^рованием,

Итак,/'(»)

^lm

ДЯ»)/Ал.

Физическом

смысле

отношение

ДДл:)/Дх

является средней скоро-

СТЫ

измен

ения

функции

Л*)

на

отрезке

[х,

х +

Д*),

Urn

ДДхУД*

=:/'/Y\

^-*°

мгновенной

скоростью

изменения

этой

функции

точке

х.

предел

слева

точке

равен

я-*

Итак,

Дх)

разрывна

каждом

целом числе

и все эти

разрывы

1-го рода.

Функция

F(x) непрерыв-

на

справа

каждой точке,

том

числе

целой

п,

где

функ-

ция

равна

нулю.

В то же

вре-

мя

предел слева

каждой

це-

лой

точке равен единице.

Итак,

F(x)

разрывна

каждом целом числе

все эти

разрывы 1-го рода.

На

языке

«е

- 8»

доказать

непрерывность функции

у -

Рассмотрите

функцию

округления

у -

0(х).

Нарисуйте

ее

график.

каких точках

у нее

разрывы? Какого рода?

Найдите асимптоты функций

Торнквиста

спроса

на

«предме-

ту

первой

необходимости»

«предметы роскоши»:

ах/(х

и),

У-

ах(х

с)/(х

-Ь

6),

где

а,

Ь>

зависят

от

цен,

а х

есть

доход.

Например,

если функция

у - Дх)

задает зависимость пути

у,

прой-

денного

некоторым телом,

от

времени

х>

то

производная

'(х)

явля-

ется

скоростью движения; если функция

дает

зависимость количест-

ва

производимой

кем-то-продукции

от

времени,

то ее

производная

является

производительностью труда.

Геометрически отношение

ДДх)/Дх

является тангенсом угла

(рис.

I),

кото-

рый

образует секущая, проходящая

через

точки

А и

осью

ОХ,

Если

0, то

точка

стремится

точке

А, а

угол

стремится

углу

а,

который образует

ка-

сательная

графику функции

точке

А с

осью

ОХи,

следовательно,

lim

ДДх)/Дх-

Дх->0

lim

tgcc

= tg

cc.

Отсюда

получаем

В-*А

f'(x)

= tg a = k

(геометрический

смысл

производной),

где k —

угловой

коэффи-

циент

касательной

графику

функции

Дх) в

точке

х,

Следовательно, уравнение касательной

графику

функции

=Дх)

точке

есть

/(х

)(х

Функция

-f(x)

называется

дифференцируемой

точке

х,

если

ее

приращение

этой точке можно представить

виде

ДДх)

ЛДх

аДх,

где

А —

константа,

а а —

бесконечно малая функция (б.м.ф.)

при

Дх-»0.

Теорема

Необходимым

достаточным

условием

дифференциро-

вания

функции

некоторой

точке

является

существовв'

пне

ее

производной

этой

точке.

Доказательство

необходимости. Пусть функция

у - Дх)

диффе-

ренцируема

точке

х.

Тогда ДДх)

А Дх

«Ах,

где

<х

—

б.м.ф.

пр"

Дх

Тогда

ДДх)/Дх

А + а.

Отсюда

по

обратной лемме (см.

п. 3,

раздел_4.3)

НтДх)/Дх=

А,

т.е.

производная

функции

существует,

Доказательство

достаточности. Пусть существует

производная

функции/'(х)

= lim

ДДх)/Дх.

Согласно лемме

(см.

также

п. 3

разде-

Дх->0

ла

4,3)

ДДх)/Дх

=/'(*)

«,

где а -

б.м.ф.

при

Дх

-»

или

ДД^)

-/'(х)Дх

аДх,

т.е.

функция

дифференцируема

точке

х.

Замечание,

ходе

доказательства

также

получено,

что

длядиФФ

ренцируемой

функции

равенство

(1)

можно

записывать

виде

АД*)

-/(*)Дх

аДх,

где

а -

б.м.ф,

при

Теорема

Если

функция

дифференцируема

точке,

то

она

непре-

рывна

пей,

Доказательство,

Если функция

=/(х)

дифференцируема

точ-

ке

х, то

ДДх)

/'(х)Дх

аДх,

где а —

б.м.ф.

при

Д*

-»

Откуда

lim

ДДх)

т.е. функция непрерывна

точке

х.

&х->й

Применение производной

экономике. Рассмотрим однофак-

торную,

или

одноресурсную,

производственную

функцию

-Л*),

которая

дает

объем

производимой продукции

за

единицу времени

зависимости

от

объема

затраченного ресурса.

Этот

ресурс весъма

часто

—

количество живого человеческого

труда,

выраженного

виде

человеко-часов

или

числа работников. Пусть

нынешнем состоянии

число

работников фирмы равно

а.

Обычно производственные функ-

ции

дифференцируемы,

так

чтоУ(й

+ 1)

/'(«)•

Если число

работников

велико,

то

вышенаписанное приближенное равенство

довольно точное.

Но что

такое/'(о)

этом случае?

Это не что

иное,

как

добавочная продукция, производимая новым сотрудником пред-

приятия

за

единицу времени.

Пусть

v —

цена единицы

продукции,

зарплата работника

за

единицу времени. Тогда, если

v/'(e)

> Л то

надо

нанять

еще од-

ного

сотрудника,

так как он

приносит фирме

больше,

чем она ему

платит.

Это

несложное правило имеет

универсальный

характер

называется

золотым правилом

экономика,

Вообще

рассматриваемой ситуации производную производст-

венной

функции

точке

а в

экономике называют предельной

произ-

водительностью труда (при размере фирмы

я), в

отличие

от

средней,

которая

равна

J(a)/a.

„

Рассмотрим некоторые

введенные

функции (см.

п. 2

раздела 4.2)

определим экономический смысл

их

производных.

Функция

спроса

-ОД

зависимость спроса

D на

некото-

рый

товар

от его

цены

р.

Производная

D(p)

дает

приблизительно

увеличение

спроса

при

увеличении

цены

на

одну

единицу.

Посколь-

ку,

как

известно,

при

повышении цены спрос уменьшается,

то на

самом

деле

абсолютное значение производной показывает уменьше-

ние

спроса

со

стороны покупателей

на

товар

при

повышении

его

Цены

на

одну единицу.

Функция

предложения

ЭД -

зависимость предложения

некоторого товара

от его

цены

р.

Производная

S(p)

дает

приблизи-

тельно

увеличение предложения товара

со

стороны продавцов (про-

изводителей)

при

увеличении

цены

на

одну

единицу.

Функция

полезности

и(х)

субъективная числовая

оценка

дан-

ным

индивидом полезности

количествах

товара

для

него. Производ-

нал

и'(х)

дает

приблизительную

оценку дополнительной полезности

от

приобретения

еще

одной единицы товара.

Налоговая

ставка

—

зависимость налога

процентах

от

вели-

чины

годового

дохода

Пусть

—

сами

значение налога, которое

надо

платить

годового

дохода

Тогда производная

Р и

есть нало-

говая

ставка

Производная

функции

~f(x)

дает

величину мгновенной ско-

рости

изменения пройденного

за

время

пути

у,

производная произ-

водственной

функции

дает

предельную производительность труда

т.д.

Но в

экономике чрезвычайно

удобно

задавать такие вопросы:

на

сколько процентов изменится спрос

на

товар,

если цена

на

него

увеличится

на

\%1

На

сколько процентов изменится

предложейие

товара, если цена

на

него увеличится

на

\%1

т.д.

Такие вопросы

ответы

на них

вводят новое понятие «эластичность функции

по ар-

гументу»

или

относительная

производная,

Рассмотрим

функцию

f(x).

Пусть

Дх

—

приращение аргу-

мента,

ДА» —

соответствующее приращение функции. Тогда

Дх/х

относительное изменение аргумента,

Д/(х)/Лх)

—

относительное

из-

менение

функции. Величина

(ДДх)/Лх))/(ДхД)

—

отношение отно-

сительного изменения функции

относительному изменению аргу-

мента

—

называется средней эластичностью функции

по

аргументу

на

отрезке

[х, х

Дх],

предел

этого

отношения

при Дх

т.е.

Нт

(ДДх)/Лх))/(Дх/х)

=/'(х)/(Ах)/х)

называется

эластичностью

функции

у по

аргументу

точке

х и

обозначается

Следовательно,

если

эластичность спроса

на

товар

по

цене равна

-2, это

означает,

что при

повышении данной цены

на 1 %

спрос

уменьшится

на

1%-

если эластичность выпуска продукции

по

труду равна

ото

озна-

чает,

что для

увеличения выпуска продукции

на

надо

увеличить

количество

работников

на 2%,

Пример!.

Для

функции спроса

D - 40 -

2/>

найти эластичность спро-

са

по

цене

при р = 4.

Решение,

Я*

(4)

Я'(4)/(Я(4)/4)

-2/8

-1/4.

Правила

дифференцирования

(нахождения

производных

функ-

ций).

Производные основных

элементарных

функций:

постоянная величина:

С'=

степенная функция;

(х

)'^

ах

;

показательная функция:

(я*)'

дМп

я;

показательная функция

основанием

е:

)'»

;

логарифмическая функция

натуральным логарифмом:

(In

*)'=!/*;

логарифмическая функция:

(log

х)'

(l/x)ln

а;

тригонометрические функции: (sin

х)'

cos

(cos

х)'

-sin

(tg

x)'

I/cos

(ctg

x)'

-I/sin

Структурные

правила

дифференцирования:

производная суммы:

(Дх)

g(x»'

-/'(х)

S'(x)l

производная произведения:

(Дх^х))'^/'(*)#(*)

+Лх)ё'(х)1

производная частного:

№)/g(x))

(Г

Шх)

-Mg'WW

(*);

производная сложной функции:

(и(/М)'-

«'№))/'(*);

производная обратной функции:

1/х'.

Вывод этих правил можно посмотреть

учебниках.

Производные

неявных

параметрических

функ-

ций.

Пусть функция

у -

'у(х)

задана неявно

при

помощи

уравнения

Д*,

у)

= 0.

Чтобы

найти

ее

производную,

нужно

это

равенство про-

дифференцировать

по х с

учетом

зависимости

от

х и

затем решить

полученное

уравнение относительно

Пример

Найти

у'

от

неявной функции

+ у +

cosy^

sin x.

Решение.

Продифференцируем данное равенство

по х,

затем

найдем

у;.

•

(

у)

х,

откуда

у'

cos

хДе

+ 1 -

sin

у).

Функция

у(х) называется

параметрической,

если значения

Функции

значения аргумента задаются

при

помощи

функции

от

вспомогательной

величины

называемой

параметром:

х -

х(0

ХО.

Правило

нахождения производной параметрической функции;

если

существуют

х'(0

/(/),

то

у'

y'Wfo'W

(*'(0

°^'

Пример

Найти

у'от

функции

X*),

заданной

параметрически:

*(')

4Г

ХО

1. ,

/м

,з

л.

п/л

Решения

х'(0

12/*,

/О)

2/,

значит,

у'

2//(4/

12/)

1/(2/

б/).

Производные

высших

порядков.

Производная функ-

ции

)

является новой функцией того

же

аргумента

(х).

Про-

изводная

этой функции называется

производной

2-го

порядка

по от-

ношению

исходной

функции

(/(*»'и

она

обозначается

(х) или

/"(*).

Аналогично определяются производная 3-го

порядка,

произ-

водная

4-го порядка

дальнейшие производные.

ЗАДАЧИ

В'широко известном романе

Д.

Гранина

«Иду

на

грозу»

глав-

ный

герой Сергей Крылов, исключенный

из

института

за

непосеще-

ние

лекций, ушел работать

на

завод. «Завод

переживал

неприятности

приводами

новой серии специальных контактов. Проходя

по

цеху,