Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем

Подождите немного. Документ загружается.

В разных системах единиц измерения формула размерности для

одной и той же величины может содержать различное число аргу-

ментов и иметь разный вид. При этом формулы размерности физи-

ческих величин имеют вид степенных одночленов. Например, для

любой размерной физической величины



, зависящей от трех ос-

новных величин







, формула размерности имеет вид

















knm

  ,

где

- вещественные числа.

Физические закономерности, устанавливаемые теоретически

или экспериментально, представляют собой функциональные зави-

симости между величинами, характеризующими изучаемый объект.

Численные значения этих размерных величин зависят от выбора

системы единиц измерения и не связаны с сущностью явления. По-

этому функциональные зависимости, составляющие модель объек-

та, должны обладать специальной структурой.

Пусть имеется функциональная связь между



размерными

величинами

a ,…,

a , не зависящая от выбора системы единиц

измерения:





nkk

aaaaFa ,...,,,...,

11 



, (2.30)

где







величин

aa ,...,

имеют независимые размерности.

Независимость размерностей означает, что формула, выра-

жающая размерность одной из величин, не может быть представ-

лена как комбинация в виде степенного одночлена из формул раз-

мерности для других величин. Примем

независимых величин

aa ,...,

за основные величины и введем для их размерностей обо-

значения





kiAa

,...,1,



Размерности остальных величин будут иметь вид





AAa ...

 ;





AAa ...





;

………………





AAa ...

 .

Изменим единицы измерения величин

a ,…,

a в



,…,



раз. В новой системе единиц численные значения всех величин бу-

дут равны:

111







;

 ...





;

222







;

………….

...







 ;

…………………………

kkk







 ...





В новой системе единиц соотношение (2.29) примет вид









 nkk

mmm

aaaaFaa

,...,,,...,......

2121







aaaaF

 ...,...,...,,...,

2121

11 

. (2.31)

Уравнение (2.31) показывает, что функция

обладает свойст-

вом однородности относительно масштабов



, …,



. Так как

масштабы



, …,



произвольны, воспользуемся их выбором для

сокращения числа аргументов у функции

. Согласно предполо-

жению о независимости соотношения (2.30) от системы единиц из-

мерения установим новую систему единиц измерения так, чтобы

аргументов у функции

имели фиксированные постоянные зна-

чения, равные единице. В этом случае уравнение (2.30) может быть

представлено в виде соотношения между





величинами П,

П ,…,

n-k

П , представляющими собой безразмерные комбинации из



размерных величин

a ,…,

a :





















F ПП,П ,...,1,...,1

. (2.32)

Численные значения параметров определяются формулами

aaa

...

П ;

aaa

...

1



П ;

………………….

n-k

aaa

...

П ,

где

a ,…,

a - численные значения рассматриваемых величин в

первоначальной системе единиц измерения. Значения П,

П ,…,

kn

П не зависят от выбора первоначальной системы единиц изме-

рения, так как они имеют нулевую размерность относительно еди-

ниц измерения

A ,

A ,…,

A . Кроме этого значения

П ,…,

kn

вообще не зависят от выбора системы тех единиц измерения для

величин

a ,

a ,…,

a . Следовательно, эти величины можно рас-

сматривать как безразмерные.

Таким образом, связь между



размерными величинами

a ,…,

a , не зависимая от выбора системы единиц измерения, при-

нимает вид соотношения (2.32) между





величинами

П ,…,

kn

П , представляющими собой безразмерные комбинации из



размерных величин. Этот общий вывод теории размерности носит

название П-теоремы.

В соотношении (2.32) путем изменения функции

систему без-

размерных параметров

П ,…,

kn

П можно заменять другой систе-

мой безразмерных параметров, являющихся функциями



па-

раметров

П ,…,

kn

П .

Всякое физическое соотношение между размерными величи-

нами можно сформулировать как соотношение между безразмерны-

ми величинами. В этом заключается важнейшее прикладное значе-

ние теории размерности.

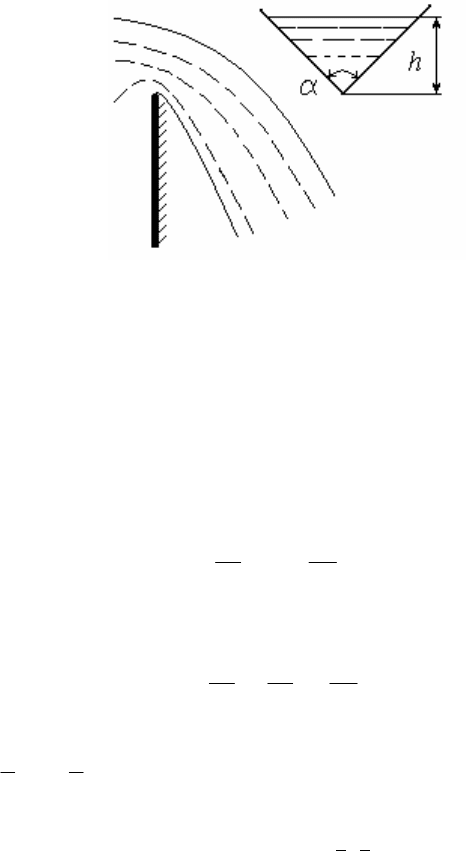
Пример 2.1. Истечение тяжелой жидкости через водослив.

Водослив (рис.2.1) представляет собой вертикальную стенку с

треугольным отверстием, расположенным симметрично относи-

тельно вертикали, причем угол отверстия



равен 90. Жидкость

вытекает под напором

, который равен высоте уровня жидкости

над вершиной треугольника. Примем, что резервуар, в котором на-

ходится жидкость, очень большой, и поэтому движение жидкости

можно считать установившимся.

Установившееся течение жидкости через водослив полностью

определяется плотностью жидкости



, ускорением свободного па-

Рис. 2.1. Перетекание тяжелой жидкости через водослив

дения

и напором

. Поэтому массовый расход жидкости Q (мас-

са жидкости, вытекающей в единицу времени) является только

функцией этих параметров:





hgFQ ,,





Размерности определяющих параметров в классе

име-

ют вид:

 

 ;

 

g  ;







; .

Составим формулу размерности с использованием простейшего

степенного одночлена

 



























Из последнего уравнения легко определяются числа



;

n ;

k . Поэтому с точностью до постоянного множителя

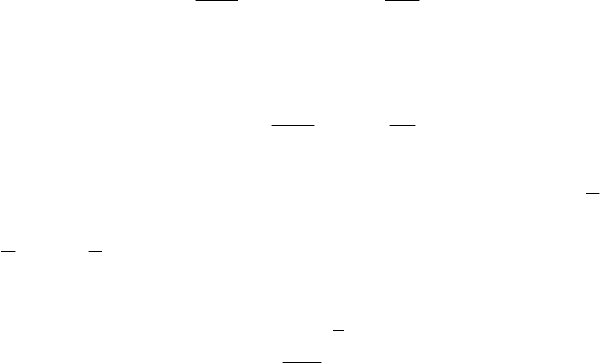
формулу для расхода жидкости можно представить в виде

 

hgCQ  ,

где коэффициент







C , в общем случае зависящий от угла



, опре-

деляется экспериментально.

Пример 2.2. Распространение ударной волны.

При атомном взрыве в малой области, которую можно считать

точкой, быстро (практически мгновенно) выделяется значительная

энергия

. От центра взрыва распространяется мощная ударная

волна, давление за которой составляет сотни тысяч атмосфер. Атмо-

сферным давлением воздуха можно пренебречь, поэтому радиус

фронта ударной волны

через промежуток времени



после взрыва

зависит от



и начальной плотности воздуха











,,EFr



Размерности определяющих параметров в классе

имеют

вид:

 

E  ;









;

 

 .

Составим формулу размерности с использованием простейшего

степенного одночлена

 



























Из последнего уравнения легко определяются числа

m ;

n ;

k . Поэтому с точностью до постоянного множителя

получаем формулу

















E

Cr ,

где

const



. Экспериментально установлено, что



Инвариантность моделей по отношению к системе единиц из-

мерения — частный случай более общих свойств их симметрии.

Расширение понятия подобия основано на следующем математиче-

ском условии соответствия:

,,),,( BaRxaxfxTx





(2.33)

где

– N-мерное евклидово пространство;



– открытый шар с центром в точке

R0

;

T – преобразование пространства

в себя;





aaa ,...,



– параметры отображения

RBRf  (2.34)

Использование условия (2.34) приводит к более сложному ап-

парату определения взаимосвязей между объектами и их моделями.

Конкретное решение этих вопросов зависит от принятых ограниче-

ний на свойства оператора

T . Перспективным направлением ре-

шения этих вопросов являются применение теоретико-группового

анализа.

Если принять, что при малых





 а выполняются соот-

ношения композиции

,)),,()()( xTabfxfxTTbTT

cbaba



и условия существования обратного и тождественного преобра-

зований

,)0,(,)),,((

xxfxaaxffxTT





то преобразование вида f образует локальную r-параметрическую

группу Ли

G .

Свойства группы Ли

полностью определяются составля-

ющими ее однопараметрическими подгруппами

G , среди которых

имеет место группа масштабных преобразований, для которой вы-

ражения (2.33) – (2.34) сводятся к преобразованию (2.29). Это озна-

чает, что классическая теория подобия может быть изложена в тер-

минах группы масштабных преобразований, а также развита на ос-

нове общего аппарата групп непрерывных преобразований.

Применение непрерывных групп преобразований к дифферен-

циальным уравнениям дает возможность эквивалентного перехода к

более простым их формам. Если исходное дифференциальное урав-

нение обыкновенное, то возможно понижение его порядка. В неко-

торых случаях возможно сведение краевой задачи к задаче Коши.

Если задано дифференциальное уравнение в частных производных,

то знание непрерывной группы преобразований позволяет редуци-

ровать его к уравнению, содержащему меньшее число независимых

переменных, нежели в исходном уравнении. В ряде случаев нели-

нейное уравнение, обладающее групповым свойством, можно ли-

неаризовать.

Пример 2.3. Понижение порядка дифференциального уравне-

ния. Рассмотрим линейное дифференциальное уравнение второго

порядка с переменными коэффициентами

.0)()(

 uxb

(2.35)

Уравнение (2.35) допускает группу

G :

ueuxx  ';' с опера-

тором





Оператор продолженной группы G

имеет вид









Инвариантом группы

является функция I

= x, инвариант

группы

G , есть решение уравнения









откуда



Будем искать решение уравнения (2.35) в виде I

= I

)=I(x). В

этом случае

,,)(

uxIu







а исходное уравнение примет вид

.0)()(

 xbIxaI

Таким образом, порядок исходного уравнения понизился на

единицу.

Пример 2.4. Редукция уравнения в частных производных к

обыкновенному дифференциальному уравнению. Уравнение рас-

пространения тепла в тонком однородном стержне имеет вид







(2.36)

где k - коэффициент, характеризующий теплофизические свойства

материала стержня.

Уравнение (2.36) допускает группу G

uuxextet

 ';';'

с оператором









Эта группа имеет два алгебраических инварианта:

uIxtI 



Относительно инвариантов уравнение (2.36) записывается в

виде



Таким образом, исходное уравнение в частных производных

редуцировалось к обыкновенному дифференциальному уравнению.

2.3. Неэквивалентные преобразования моделей

В основе методов неэквивалентного преобразования моделей

лежит возможность упростить исходное математическое описание

путем определения и исключения тех ее компонентов, которые не

оказывают существенного влияния на результат моделирования.

При реализации этого подхода производится аппроксимация

исходной модели более простым описанием, т.е. происходит замена

Ф

, исходя из минимизации выбранного критерия близости

.min),(

 ФФF

При исследовании и моделировании различных систем практи-

чески всегда приходится искать компромисс между сложностью

математического описания и точностью результатов. В этих случаях

выбор модели осуществляется из множества возможных описаний,

различающихся типами уравнений.

При моделировании сложных распределенных объектов, как

правило, используются дифференциальные уравнения в частных

производных, которые в общем случае могут быть представлены в

виде

,0,...),,...,,,...,,,(



yyxxyx

uuuuuzyxФ

где ,...),,( zyxuu



- искомая функция нескольких переменных.

Такие модели получаются на основе использования физических

законов и имеют очень высокие возможности аналитического опи-

сания процессов. Однако практическое их использование обычно

сопряжено с большими трудностями как аналитического, так и вы-

числительного характера. Поэтому широкое распространение полу-

чили многочисленные методы упрощения. К ним относятся:

- редукция нелинейных дифференциальных уравнений к

обыкновенным дифференциальным уравнениям;

- понижение размерности;

- дискретизация (переход от непрерывного описания к дис-

кретному);

- континуализация (переход от дискретного описания к не-

прерывному);

- переход от дифференциальных уравнений к интегральным;

- линеаризация.

При выполнении неэквивалентных преобразований моделей

необходимо учитывать следующие обстоятельства.

При упрощениях моделей требуется оценка получаемых при

этом погрешностей. Обычно эта процедура представляет собой са-

мостоятельную задачу, для решения которой могут использоваться

как точные, так и приближенные методы.

Математическая строгость, корректность и точность при моде-

лировании не являются самоцелью, как это имеет место, например,

при решении дифференциальных уравнений. Основная роль при-

надлежит физическому содержанию задачи. Поэтому главным спо-

собом результатов моделирования служит опытная проверка.

Полнота математического описания и точность задания исход-

ных параметров являются связанными вопросами, которые могут

вступать в противоречие. Это обусловлено тем, что усложнение ма-

тематического описания повышает чувствительность решений к

отклонениям параметров, которые обычно определяются экспери-

ментально и имеют вероятностный характер. В ряде случаев реаль-

ная точность результатов моделирования при точной аналитической

модели оказывается более низкой, чем при использовании упро-

щенного математического описания.

2.4. Линеаризация уравнений автоматических систем

Практически все реальные элементы автоматических систем

имеют нелинейные характеристики и поэтому описываются нели-

нейными дифференциальными уравнениями. В связи со сложно-

стью анализа нелинейных систем большое значение имеют при-

ближенные методы их исследования, основанные на замене нели-

нейных соотношений линейными и привлечении простых и хорошо

разработанных методов линейной теории.

На практике используются следующие методы линеаризации.

Статическая линеаризация (линеаризация касательными),

при которой нелинейная характеристика в окрестности нормального

рабочего состояния (рабочей точки) заменяется линейной зависимо-

стью, определяемой касательной в данной точке.

Гармоническая линеаризация, используемая при исследова-

нии установившихся колебаний в нелинейных системах. В основу

метода положено фильтрующее свойство линейной части замкнутой

системы. Высокочастотные гармонические составляющие подавля-

ются инерционными линейными звеньями. Это позволяет считать,

что в системе в установившемся состоянии действуют только сину-

соидальные сигналы основной частоты. В этом случае нелинейная

система приобретает свойства линейной.

Статистическая линеаризация, основанная на приближении

характеристик случайных сигналов линейными зависимостями.

Несмотря на большие преимущества методов линеаризации,

обеспечивающие им широкое использование на практике, они име-

ют и ряд серьезных недостатков: