Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем
Подождите немного. Документ загружается.

41
.),,(
2
1
t
t
ii
dttqqLS
(2.5)
Согласно принципу наименьшего действия система между по-
ложениями
1
tq
i
и
2
tq
i
,
n
i
,...,
1
, движется таким образом, что
действие (2.5) имеет наименьшее возможное значение. Это означает,
что точка, изображающая состояние системы, движется в конфигу-
рационном пространстве по той траектории, для которой действие S
минимально. Такая траектория носит название прямого пути, все
остальные траектории называются окольными путями.
Из (2.5) следует, что размерность действия равна размерности
произведения энергии на время (или импульса на перемещение).
Такую же размерность имеет постоянная Планка, которую называ-
ют квантом действия.
Действие S представляет собой функционал. Он достигает экс-
тремального значения при условии, что его вариация равна 0, т.е.
.0),,(
2
1
dttqqLS
t
t
ii
Таким образом, в терминах вариационного исчисления прямой
путь является экстремалью, а отвечающее ему число – стационар-
ным значением функционала S.
Справедливо утверждение, обратное принципу наименьшего
действия: если для некоторой траектории выполняется свойство
0
S
, то эта траектория является экстремалью.
Законы сохранения
В основе законов сохранения лежат свойства пространства и
времени. Сохранение энергии связано с одномерностью времени,
сохранение импульса – с одномерностью пространства, сохранение
момента импульса находится в связи с изотропией пространства
(изотропия означает одинаковость свойств в каждой точке по всем
направлениям).
Теорема Нётер. Рассмотрим однопараметрическое преобразо-
вание системы отсчета
q
,
t
:
,,tqq
ii
;
n
i
,...,
1
;
,,tqt
, (2.6)

42
такое, что оно тождественно при
0
и для него существует об-
ратное преобразование.
Пусть лагранжиан заданной механической системы, движущей-
ся в потенциальном поле, инвариантен относительно преобразова-
ний координат (2.6). Это означает, что новый лагранжиан
tqqL ,,
не зависит от
и как функция переменных tqq ,,
имеет
тот же вид, что и исходный лагранжиан в переменных tqq ,,
. Тогда
существует функция от
t
q
p
,
,
0
0
1
,,
i
n
i
i
i
Hptpq , (2.7)
не изменяющая на прямых путях своего значения с течением време-
ни (первый интеграл движения).
Из теоремы Нётер следует закон сохранения полной механиче-
ской энергии для систем, лагранжиан (так же как и гамильтониан)
которых явно не зависит от времени, или консервативных систем.
Это утверждение легко доказывается применением в (2.6) сдвига по
времени
ii
qq
;
n
i
,...,
1
;
tt
.
В этом случае из (2.7) следует
const
пк
WWH
.
Аналогичным образом доказываются закон сохранения количе-
ства движения для замкнутой (не испытывающей действия внеш-
них сил) системы и другие законы механики.
Закон сохранения энергии. Выражение энергии через функ-
цию Лагранжа имеет вид
tqqLq
q
L
E
ii
n
i
i
i
,,
1
. (2.8)
Пусть система частиц находится в неизменных внешних усло-
виях: система замкнута или подвержена действию постоянного
внешнего силового поля, связи идеальны и стационарны. В этом
случае время в силу своей однородности не может входить явно в
функцию Лагранжа. Для такой системы
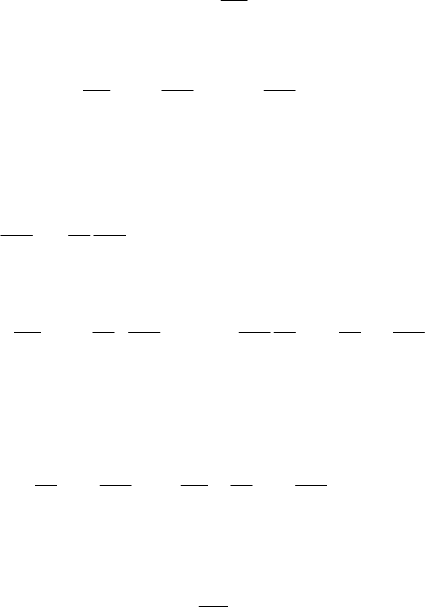
43
0
t
L
и, следовательно,
n
i
i
i
n
i
i
i
q
q
L
q
q
L
dt
dL
11
. (2.9)
Если система консервативна, движение частиц подчиняется
уравнениям Лагранжа (2.3). Заменим в соответствии с этими урав-
нениями
i
q
L
на
i
q
L
dt
d
в формуле (2.9) и получим выражение
n
i
i
i
n
i
i
i
n
i
i
i
q
q
L
dt
d
q
dt
d
q
L
q
q
L
dt
d
dt
dL
111
,
которое можно представить в виде
0
11
Lq
q
L
dt
d
dt
dL
q
q
L
dt
d
n
i
i
i
n
i
i
i
.
С учетом (2.8) имеем
0
dt
dE
,
откуда
const
E
.
Таким образом, из однородности времени вытекает закон: энер-
гия замкнутой (или находящейся в стационарном внешнем силовом
поле) консервативной системы частиц остается постоянной. Энер-
гия замкнутой системы является интегралом движения.
Закон сохранения импульса. Рассмотрим замкнутую систему
частиц, для которой воздействие внешних тел на частицы пренеб-
режимо мало. Произведем над системой малый параллельный пере-
нос на вектор
. При таком преобразовании все точки системы
смещаются на один и тот же вектор
ii
rr . Изменение функции
Лагранжа в результате такого преобразования имеет вид
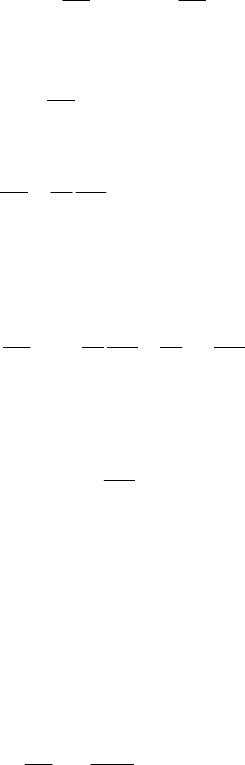
44
n
i
n
i
i
i
i
r
L
r
r
L
L
1 1
.
По предположению
0
, следовательно
0
1
n
i
i
r
L
. (2.10)
В соответствии с уравнениями Лагранжа
ii
v
L
dt
d
r
L
, (2.11)
где
i
v
- вектор скорости
i
-й частицы.
Выражение (2.11) можно представить в виде
0
111
n
i
i
n
i
i
n
i
i
v
L
dt
d
v
L
dt
d
r
L
.
Из полученного выражения следует, что векторная величина
n
i
i
v
L
p
1
(2.12)
остается неизменной в процессе движения. Эта величина есть сум-
марный импульс системы.
Таким образом, в силу однородности пространства следует за-
кон: суммарный импульс замкнутой системы частиц остается по-
стоянным
p
const.
Уравнение (2.10) имеет простую физическую интерпретацию.
Если кинетическая энергия системы не зависит от
r
, то производ-
ная лагранжиана равна
i
ii
F
r
W
r
L
п
.
Поэтому условие (2.10) имеет вид
n
i
i
F
1
0
.
Полученное уравнение есть третий закон Ньютона.

45
Закон сохранения момента импульса. Вследствие изотропии
пространства механические свойства замкнутой системы частиц не
должны изменяться при произвольном повороте системы как целого
в пространстве. При этом не должна изменяться и функция Ла-
гранжа. Определим приращение функции Лагранжа
L
при произ-
вольном малом повороте системы на угол
. При повороте систе-
мы изменяется направление не только радиусов-векторов, но и ско-
ростей всех частиц, причем все векторы преобразуются по одинако-
вому закону. Определим приращение функции Лагранжа
L
при
произвольном малом повороте системы на угол
. При повороте
системы изменяется направление всех векторов и скоростей частиц.
При этом
ii
rr
,
;
ii
vv
,
. (2.13)
Вследствие малости величин
i
r
и
i
v
имеем выражение
i
n
i
i
i
n
i
i
v
v
L
r
r
L
L
11
,
которое с учетом (2.13) принимает вид
i
n
i
i
n
i
i
i
v
v
L
r
r
L
L
,,
11
.
Выполнив в последнем уравнении перестановку сомножителей
и преобразование переменных в соответствии с уравнениями Ла-
гранжа, получим соотношение
.,,,
11 1
n
i
i
i
n
i
n
i
i
i
i
i
v
L
r
dt
d
v
L
v
r
L
dt
d
rL
Так как по предположению 0
, то, следовательно,
0
L
,
или

46
n
i
i
i
v
L
r
dt
d
1
,
и
const
n
i
i
i
v
L
r
1
,
.
Согласно (2.12) выражение
i
v
L
есть импульс
i
p
. Величина
iii
prM
есть момент импульса частицы относительно начала
координат. Следовательно, для результирующего импульса системы
справедливо выражение
const
n
i
ii
n
i
i
prMM
11
.
Таким образом, в силу изотропии пространства имеет место за-
кон: результирующий момент импульса замкнутой системы частиц
остается постоянным. Момент импульса замкнутой системы, так же
как энергия и импульс, является интегралом движения.
Уравнения газа и жидкости
При описании динамики большого числа материальных частиц
преимущественное использование имеют подходы, рассматривающие
не
поведение каждой отдельной частицы, а лишь средние характери-
стики системы такие, как плотность, скорость, температура и т.п.
Для этого вводится статистическое вероятностное описание ан-
самбля частиц с помощью функции распределения
tvrf ,,
,
где
r
и
v
- радиус-вектор и скорость соответственно. Функция
f зависит от «координат» шестимерного фазового пространства х,
у, z,
x
v ,
y
v ,
z
v (пространства состояний) и времени. Величина
vdrdtvrf
,,
по определению равна числу частиц, находящихся в момент t в элемен-
те
vdrd
фазового пространства, т.е. имеющих координаты в интер-
вале от
r
до
rdr
и скорости в диапазоне от
v
до
vdv
. Элемент
vdrd
считается малым в сравнении с характерными размерами сис-
темы, но содержащим достаточно большое число частиц.

47
Функция распределения служит основой для определения мак-
роскопических величин, описывающих состояние газа. Например,
число частиц, находящихся в единице физического объема с коор-
динатой
r
в момент времени t, определяется по формуле
vdtvrftrn
,,, .
Скорость газа определяется по выражению
1
,,,
nvdtvrfvtrV
.
Основой математического описания динамики газов служит
кинетическое уравнение Больцмана
для функции распределения.
В его основе лежат следующие допущения:
- время столкновения (непосредственного эффективного сило-
вого взаимодействия) частиц много меньше времени, проходящего
между их столкновениями;
- влиянием внешних сил, действующих на частицы (гравитаци-
онных, электрических и т.д.), можно пренебречь;
- частицы идентичны, не расщепляются и не объединяются.
Возможность столкновений частиц учитывается с помощью
интеграла столкновений
fS . Величина
dtvdrdfS
есть
разность между числом частиц, вышедших благодаря столкновени-
ям за время
dt
из объема
vdrd
(и не попавших в объем
vdrd
), и
числом частиц, попавших из-за столкновений за время dt в объем
vdrd
(и не находившихся в первоначальном объеме
vdrd
).
Уравнение Больцмана имеет вид
0
fS
r
f
v
t
f
. (2.14)
Оно представляет собой нелинейное интегро-дифференциальное
уравнение. Его конкретная запись зависит от характера столкнове-
ний частиц, т.е. от вида функции
fS . Формула (2.14) легко обоб-
щается на газ, состоящий из частиц разного типа, и на случай, когда
внешняя сила
F
отлична от нуля (она может быть вызвана, напри-
мер, наличием электромагнитных полей). При отсутствии столкно-
вений, т.е. при
0
fS , уравнение (2.14) эквивалентно уравне-

48
нию переноса, описывающему поток вещества и отвечающему зако-
ну сохранения массы.
Гидродинамическая модель газа, основанная на уравнении
Больцмана, представляет собой систему из пяти уравнений:
-
уравнения неразрывности
V
dt
d
div
;
(2.15)
-
трех уравнений движения, записанных в векторной форме:
VVp
dt
Vd
graddivgrad
1
; (2.16)
- уравнения энергии
2
VVp
dt
d
divdiv
T
xxx
ji
j
j
i
i
i
i
i
graddiv
V
VV
2
2
2 , (2.17)
где
- плотность;
p – давление частиц газа;
,
- коэффициенты вязкости;
- внутренняя энергия;
;
- коэффициент теплопроводности.
При известных краевых условиях уравнения позволяют для
сжимаемого вязкого теплопроводного газа определить пять функций:
, р и три компоненты скорости V
, непосредственно характери-
зующих его гидродинамическое состояние. Полученная из исход-
ного кинетического уравнения Больцмана модель (2.15) -(2.17)
имеет простую физическую интерпретацию. Уравнение (2.15) пред-
ставляет собой форму записи закона сохранения массы жидкой
частицы. Уравнение (2.16) выражает второй закон Ньютона, приме-

49
ненный к фиксированной жидкой частице: ее ускорение определяется
суммой сил давления и вязких напряжений. Формула (2.17) описывает
изменение во времени внутренней энергии жидкой частицы за счет ра-
боты сил давления (первое слагаемое в правой части), вязкого трения
(следующие три слагаемые) и теплопередачи (последнее слагаемое).
При упрощениях рассмотренной модели получаются различ-
ные известные уравнения, широко используемые при описании ди-
намики газов и жидкостей.
При отсутствии теплопроводности
0
модель (2.15) - (2.17)
представляет собой систему уравнений Навье—Стокса для вязко-
го сжимаемого нетеплопроводного газа. Для важного частного случая
несжимаемой жидкости
const,
tr
из (2.15) следует, что
0div V
и модель Навье—Стокса состоит из четырех уравнений
Vp
dt
Vd
grad
1
; 0div V
,
(2.18)
а уравнение энергии (2.17) заменяется заданной зависимостью
p
.
Если силы давления много больше сил вязких напряжений,
можно принять допущение 0
. В этом случае уравнения (2.18)
упрощаются и принимают следующий вид:
p
dt
Vd
grad
1
; 0div V
, (2.19)
Модель (2.19) совместно с уравнением неразрывности (2.15)
представляет собой систему уравнений Эйлера для несжимаемой
жидкости.
Если движение потенциально, т.е. существует скалярная
функция
tzyx ,,,
, такая, что
gradφV
(при этом
0rot V
)
,
то
система (2.19) представляет собой
уравнение Лапласа
для потенциа-
ла
:
0
.
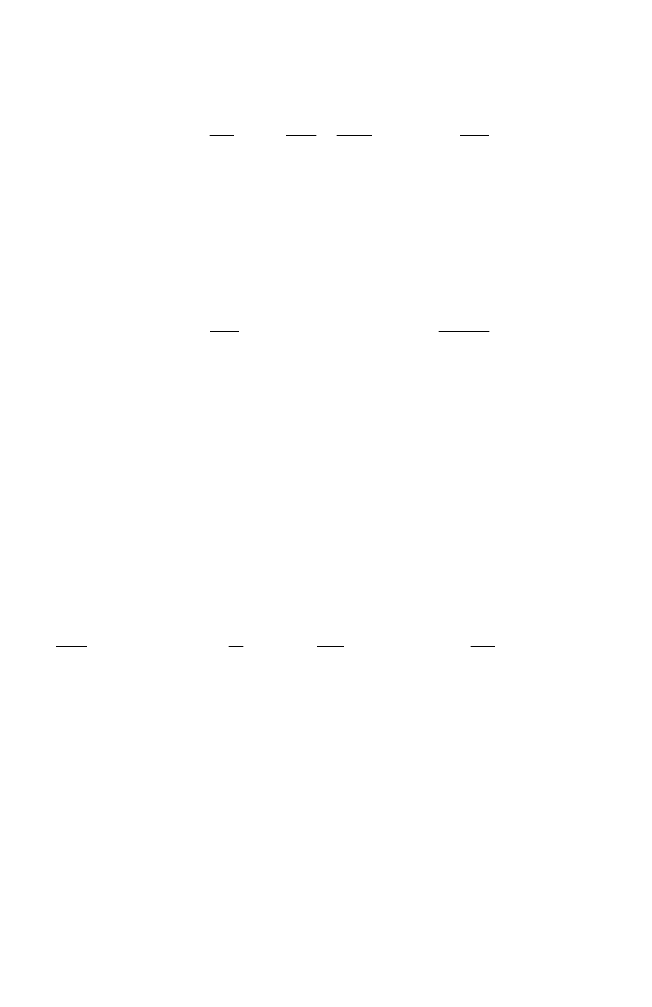
50
При отсутствии вязких свойств вещества система (2.15) - (2.17)
описывает динамику сжимаемого теплопроводного газа. В этом
слу-
чае уравнение энергии имеет вид
x
W
x
V
p
dt
d
;
x
T
W
и отвечает закону сохранения энергии применительно к жидкой
частице.
В случае неподвижной среды ( 0V
) имеем уравнение теп-
лопередачи
T
t
T
C graddiv
;
T
T
C
.
Для стационарного процесса (при постоянных С и
) урав-
нение теплопроводности есть уравнение Лапласа для температуры
Т:
0
T
.
При отсутствии диссипативных процессов вязкости и тепло-
проводности
0;0;0
из (2.15) - (2.17) получаются
уравнения движения Эйлера для сжимаемой жидкости
pVV
t
V
gradgrad
1
; V
dt
d
div
; Vp
dt
d
div
.
Уравнения
теплопередачи
Тепловая энергия, или теплота, – это энергия хаотического
движения атомов или молекул вещества. Обмен теплом между раз-
личными участками среды или материала называется теплопереда-
чей. Процессы передачи тепла обычно рассматриваются в условиях
локального термодинамического равновесия. Такое состояние, на-
пример, для газов, имеет место в том случае, когда длина свободно-
го пробега молекул
п
много меньше размеров рассматриваемого
объекта
L
, т.е. L
п
. При этом предполагается, что тепловые
процессы рассматриваются при временах, значительно превышаю-
