Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем
Подождите немного. Документ загружается.

31
Контрольные вопросы
1. Сформулируйте определение системы и укажите ее отличи-
тельные свойства.
2. Как оценивается эффективность системы?
3. Приведите классификацию систем и примеры.
4. Какие системы называют автоматическими?
5. Что понимают под управлением в технических системах?
6. Укажите основные функциональные элементы автоматиче-
ских систем.
7. Объясните принцип работы и особенности параметрических
систем автоматического регулирования.
8. Что понимают под законом регулирования? Приведите при-
меры типовых законов регулирования в автоматических системах.
9. В каких случаях применяются одно- и многоконтурные ав-
томатические системы?
10. Дайте сравнительную характеристику систем с подчинен-
ным регулированием координат и с параллельным включением об-
ратных связей.
11. Какими свойствами характеризуется модель системы?
12. Что такое «язык модели»? Какие языки используются для
представления модели?
13. Дайте сравнительную характеристику методов моделирова-
ния.
14. Объясните сущность и области использования имитацион-
ного моделирования.
15. Укажите основные источники погрешностей при моделиро-
вании систем.
16. Какие технические средства используются при моделирова-
нии различных систем?
17. В чем состоят особенности и значение моделирования как
метода научного исследования?
18. На рис. 1.8 показана принципиальная схема параметриче-
ского стабилизатора напряжения. Составьте структурную схему
этой системы, укажите функции всех элементов.
19. На рис. 1.9 показана принципиальная схема простейшего

32
н
R
VD
u
вых
u
1
R
2VT
1VT
Рис. 1.8. Принципиальная
схема параметрического
стабилизатора напряжения
Рис. 1.9. Принципиальная схема
компенсационного стабилизатора
напряжения
компенсационного стабилизатора напряжения. Составьте струк-
турную схему этой системы, укажите функции всех элементов.
20. Составьте структурную схему генератора колебаний на не-
оновой лампе, упрощенная схема которого показана на рис. 1.10, а.
Статическая характеристика неоновой лампы приведена на рис.
1.10, б, где обозначено:
в
u - напряжение включения;
о
u - напряже-
ние отключения.
а
б
Рис. 1.10. Принципиальная схема генератора колебаний (а)
и статическая характеристика неоновой лампы (б)
21. В 1750 г. А. Майклом был разработан «зюйд-вестовый»
привод для поворота башни ветряной мельницы по ветру, эскиз ко-
торого показан на рис. 1.11. При помощи вспомогательного ветряка,
ось которого расположена под прямым углом к оси основного вет-
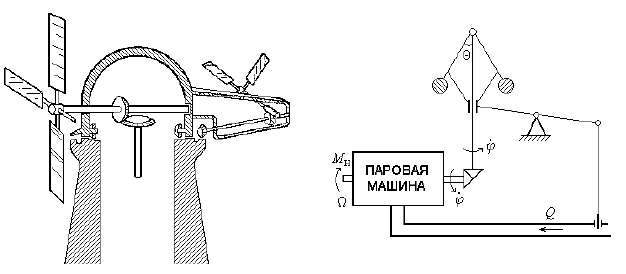
33
ряка, отклонение в направлении основной башни преобразуется в
механическое движение, которое передается с помощью редуктора к
башне. Башня вращается до тех пор, пока ось вспомогательного
ветряка не окажется расположенной под прямым углом к направле-
нию ветра.
Составьте структурную схему системы и укажите функции всех
элементов.
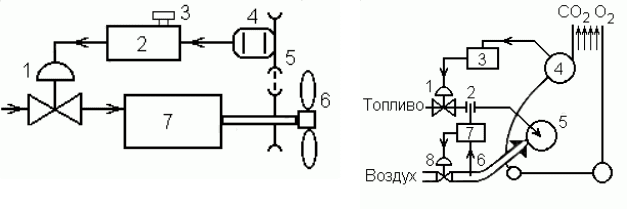
22. Упрощенная схема системы регулирования угловой скоро-
сти вращения вала паровой машины с помощью регулятора Уатта
показана на рис. 1.12. Изменение момента
н
M нагрузки приводит к
изменению угловой скорости
вращения вала машины и оси цен-
тробежного регулятора, соединенного с валом при помощи шесте-
ренчатого редуктора. При изменении скорости вращения расходятся
или опускаются шары центробежного регулятора, поднимая или
опуская муфту, которая с помощью механической передачи связана
с дроссельной заслонкой паропровода. Увеличение угловой скоро-
сти приводит к опусканию дроссельной заслонки и уменьшению
подачи пара Q , уменьшение угловой скорости вызывает подъем
дроссельной заслонки и увеличение подачи пара.
Составьте структурную схему системы и укажите функции всех
элементов.
Рис. 1.11. «Зюйд-вестовый»
привод поворота башни
ветряной мельницы
Рис. 1.12. Регулятор скорости
паровой машины
34
23. На рис. 1.13 показана упрощенная схема автоматической
системы регулирования скорости вращения судового двигателя. На
схеме обозначено: 1 – сервопривод изменения топливоподачи; 2 -
регулирующее устройство; 3 – задатчик скорости вращения; 4 – та-
хогенератор; 5 – шкив, соединяющий вал гребного винта 6 с тахо-
генератором; 7 – двигатель.
Составьте структурную схему системы и укажите функции
всех элементов.
24. На рис. 1.14 показана функциональная схема системы регу-
лирования топливосжигания в паровом котле. Давление пара в ба-
рабане 4 котла поддерживается постоянным системой регулирова-
ния давления, состоящей из регулятора с измерителем 3 и клапана
1, регулирующего подачу топлива к форсунке 5. Подача воздуха к
форсунке котла осуществляется шибером 8 по управляющему сиг-
налу регулятора соотношения 7, на входах которого действуют за-
дающий сигнал (от датчика расхода топлива 2) и сигнал обратной
связи (от датчика расхода воздуха 6). В системе регулируется и
взаимно согласовывается соотношение между количествами пода-
ваемых к форсунке топлива и воздуха.
Рис. 1.13. Автоматическая система
регулирования скорости судового
двигателя
Рис. 1.14. Система регулирова-
ния топливосжигания
в паровом котле
Составьте структурную схему системы и укажите функции всех
элементов.

35
2. АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
АВТОМАТИЧЕСКИХ СИСТЕМ
2.1. Построение математических моделей непрерывных
динамических систем
Построение математических моделей аналитическими метода-
ми основывается на использовании известных законов природы,
формализованных в виде уравнений Ньютона, Лагранжа, Кирхго-
фа, Максвелла, законов сохранения массы, энергии и импульса, за-
конов перераспределения количества тепла и энтропии. Применение
этих уравнений для конкретного объекта и преобразования позво-
ляют получить аналитическую модель в виде обыкновенных диф-
ференциальных уравнений, дифференциальных уравнений в част-
ных производных, разностных уравнений и др. Традиционная ана-
литическая модель представляет собой соотношения между «сила-
ми» (интенсивные переменные) и «потоками» (экстенсивные пере-
менные). Основные виды таких соотношений приведены в табл. 2.1.
Таблица 2.1
Основные соотношения между переменными
в динамических системах
Функции «Силы» «Потоки»
Функции
времени
Разность температур
Разность концентраций
Разность потенциалов
Поток теплоты
Поток массы
Электрический ток
Функции
времени и
координат
Градиент температуры
Градиент концентрации
Градиент потенциала
Вектор плотности потока теплоты
Вектор плотности потока массы
Вектор плотности электри-
ческого тока
Уравнения Ньютона движения механической системы
Для механической системы, состоящей из
n
материальных то-
чек, при действии каких-либо сил в соответствии со вторым зако-
ном Ньютона движение описывается системой уравнений

36
i
i
i
F
dt
rd
m
2
2
,
n
i
,...,
1
, (2.1)
где
i
m - масса
i
-й материальной точки;
i
r
- радиус-вектор
i
-й точки;
dt
rd
rtFF
ii
,, - результирующая всех сил, действующих на
точку;
r
- множество координат всех точек системы;
t
- время,
0
t
.
Система уравнений (2.1), записанная в координатной форме,
состоит из
n3
уравнений второго порядка относительно
n3
неиз-
вестных координат
tx
i
,
ty
i
,
tz
i
,
n
i
,...,
1
. Если известны на-
чальные условия, т.е. координаты точек
0
i
x ,
0
i
y ,
0
i
z ,
n
i
,...,
1
,
и их скорости
0
i
x
,
0
i
y
,
0
i
z
в момент времени
0
t
, то система
(2.1) позволяет определить координаты всех точек и их скорости
при любых
0
t
, т.е. решить основную задачу классической меха-
ники.
Уравнения движения механической системы в форме (2.1)
справедливы для инерциальной или галилеевой системы отсчета,
для которой выполняется первый закон Ньютона. В такой системе
координат материальная точка, не испытывающая каких-либо воз-
действий, движется равномерно и прямолинейно. Любая другая
система отсчета, покоящаяся или движущаяся равномерно или пря-
молинейно с постоянной скоростью по отношению к исходной сис-
теме отсчета, также является инерциальной. Для множества таких
систем, порождаемых системой отсчета tzyx ,,, , справедливы
следующие преобразования координат и времени:
axx
; byy
;
czz
;
tt
;
xx
; yy
;
z
z
;
dtt
;
sincos yxx
;
cossin yxy
;
z
z
;
tt
;
tvxx
x
; tvyy
y
; tvzz
z
;
tt
, (2.2)
где
zyx
vvvcba ,,,,, - произвольные постоянные;
- угол поворота системы отсчета относительно одной из осей
координат, например,
z
.
37
Принцип относительности Галилея утверждает равноправие
всех инерциальных систем отсчета. Этот принцип отражает одно-
родность пространства и времени и изотропность пространства (от-
сутствие в нем выделенных направлений). Последнее преобразова-
ние в (2.2) – переход к системе отсчета, движущейся с постоянной
скоростью относительно исходной, называется преобразованием
Галилея.
В неинерциальных системах отсчета второй закон Ньютона в
форме (2.1) не выполняется. Однако при модификации уравнений
(2.1) путем добавления к действующим на систему силам «фиктив-
ных» внешних сил инерции, величина которых определяется из ха-
рактера движения неинерциальной системы отсчета по отношению
к выбранной инерциальной системе, корректность уравнений меха-
ники в форме Ньютона сохраняется.
Уравнения движения механической системы называются инва-
риантными по отношению к заданному преобразованию координат,
если при переходе к новой системе отсчета не изменяется их струк-
тура и не изменяется вид функций от координат, скоростей и уско-
рений, входящих в уравнения. Если при переходе к новой системе
отсчета изменяется структура уравнений движения, но не изменя-
ется вид функций от координат, скоростей и ускорений, то такая
форма записи уравнений движения механической системы называ-
ется ковариантной по отношению к заданному преобразованию ко-
ординат.
Покоординатная форма записи уравнений (2.1) определяет их
ковариантность относительно преобразований (2.2). Однако при
более сложных преобразованиях, например, при переходе к сфери-
ческим или цилиндрическим координатам, ковариантность уравне-
ний движения в форме Ньютона утрачивается.
Уравнения Лагранжа
Для механических систем, представляющих собой множество
взаимодействующих материальных точек (частиц), характерным
свойством которых является их масса, общую форму задания со-
стояния и записи уравнений сформулировал Ж. Луи Лагранж.

38
Согласно Лагранжу состояние S механической системы описы-
вается обобщенными координатами
i
q
, i = 1,...,n, и обобщенными
скоростями
i
q
, i = 1,..., n.
Число n независимых обобщенных координат равно числу
степеней свободы системы. На частицы действуют обобщенные си-
лы
i
Q ,
i = 1,...,n, а также диссипативные силы, зависящие от скоро-
стей частиц. Уравнения движения в этом случае имеют вид
i
iii
Q
q
D
q
L
q
L
dt
d
, i = 1,..., n, (2.3)
где L - функция Лагранжа или лагранжиан, равный разности кине-
тической
к
W и потенциальной
п
W энергий системы:
пк
WWL
;
D - диссипативная функция Рэлея,
,
2
1
1
n
i
ii
qkD
i
k - коэффициент пропорциональности между скоростью i-й
частицы и диссипативной силой.
Преимущество уравнений Лагранжа (2.3) перед уравнениями
Ньютона заключается в том, что они сохраняют форму при перехо-
де к другой системе координат, т.е. являются ковариантными по
отношению к широкому классу преобразований систем отсчета.
Они позволяют получить относительно простое математическое
описание сложных механических систем в произвольных системах
отсчета, в том числе и неинерциальных, без введения дополнитель-
ных сил инерции.
Особое значение при изучении динамических систем имеет
следующее представление. Введем в рассмотрение систему коорди-
нат в воображаемом n-мерном пространстве. Такое пространство
называют конфигурационным или q-пространством. По осям этой
координатной системы будем откладывать значения координат
39
tq
i
. Тогда для каждого момента времени t состоянию системы в
обычном пространстве будет соответствовать точка в конфигураци-
онном пространстве. Движению системы в реальном трехмерном
пространстве будет соответствовать движение точки в воображае-
мом n-мерном пространстве. При этом траектория изображающей
точки зависит как от начальных значений координат, так и от зна-
чений начальных скоростей. Поэтому через каждую точку конфигу-
рационного пространства будет проходить бесконечное число тра-
екторий.
Уравнения Гамильтона
При формальном исследовании общих свойств механического
движения часто используется запись уравнений механики в виде
уравнений Гамильтона. Эти уравнения получаются в результате
перехода в уравнениях Лагранжа от одного набора независимых
переменных к другому с помощью преобразования Лежандра. Га-
мильтон получил уравнения движения, в которых независимыми
переменными являются обобщенные координаты
i
q
и обобщенные
импульсы
i
p . Уравнения Гамильтона или канонические уравнения,
в отличие от уравнений Лагранжа являются дифференциальными
уравнениями первого порядка. При описании системы с n степеня-
ми свободы число этих уравнений равно 2n.
В качестве функции, характеризующей механическую систему,
Гамильтон использовал энергию, выраженную через переменные
i
q и
i
p :
tqqLqptpqH
ii
n
i
iiii
,,,,
1
.
Функцию Н называют функцией Гамильтона или гамильтониа-
ном системы. Физический смысл функции
H
заключается в сле-
дующем. Если преобразования исходной системы стационарны, т.е.
явно не зависят от времени, то в любой момент времени гамильто-
ниан численно равен полной энергии системы
EWWH
пк
.
Обобщенный импульс
i
p
определяется выражением

40
i
i
q
L
p
,
.
,...,
1
n
i
Уравнения Гамильтона имеют вид
i
i
p
H
q
;
i
i
q
H
p
;
n
i
,...,
1
.
Полная производная от функции
H
по времени имеет вид
n
i
i
i
n
i
i
i
p
p
H
q
q
H
t
H
dt
dH
11
.
Подставив в полученную формулу выражения для
i
q
и
i
p
из
уравнений Гамильтона, получим
t
H
dt
dH
. (2.4)
Таким образом, если функция
H
явно не зависит от времени,
то согласно (2.4) она является интегралом движения.
Пространство размерностью 2n с координатами, соответст-
вующими обобщенным координатам и обобщенным импульсам
системы, носит название фазового пространства. При движении
системы в физическом пространстве со временем изменяется поло-
жение изображающей точки в фазовом пространстве. При этом тра-
ектория в фазовом пространстве однозначно определяется началь-
ной точкой. Следовательно, через каждую точку фазового простран-
ства проходит только одна траектория.
Принцип наименьшего действия
Этот принцип сформулирован в 1834 г. Гамильтоном и до на-
стоящего времени считается одним из основных принципов физики.
Действием S за интервал времени от
1
t до
2
t называют интеграл
