Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем
Подождите немного. Документ загружается.

91
кой
V
и газообразной
г
V частей смеси считаются постоянными.
При указанных допущениях уравнения баланса для концентрации
субстрата в жидкой фазе
с
N и концентрации микроорганизмов
м
N можно записать в следующем виде:
ммм0м
NNN
V
Q
N
; (2.63)
мс
мсс0с
1
S
NNN
V
Q
N
, (2.64)
где Q - расход,
1
сут.л
;
м0
N и
с0
N - начальные значения концентраций микроорга-
низмов и субстрата,
1
лмоль
;
- функция роста,
1
сут.
;
мс
S - выход микроорганизмов.
Скорость роста микроорганизмов определяется по формуле
и
2
c
сс
мсмакс
k
N
Nk
NN
v
, (2.65)
где
макс
- максимальная удельная скорость роста,
1
сут.
;
с
k - константа насыщения,
1
лмоль
;
и
k - константа ингибирования,
1
лмоль
.
Функция роста в уравнениях (2.63) и (2.64) на основании
формулы (2.65) имеет вид:
и
c
с
с
макс
1
k
N
N
k
. (2.66)

92
24
СОСН
Рис. 2.16. Схема анаэробного разложения
Присутствующие в системе микроорганизмы, откликаясь на
изменяющиеся внешние условия, например, на изменение концен-
трации субстрата, реагируют на них не сразу, а с некоторым запаз-
дыванием
. Подобная реакция с временным запаздыванием мо-
жет быть описана с помощью модифицированной функции роста
и
c
с
с
макс
1
k
tN
tN
k
. (2.67)
Уравнения (2.66) и (2.67) характеризуют изменение скорости
роста микроорганизмов в зависимости от концентрации субстрата.
Выражения (2.63) и (2.64) описывают также реактор проточно-
го типа с полным перемешиванием в случае ферментативной реак-
ции, ингибируемой субстратом.
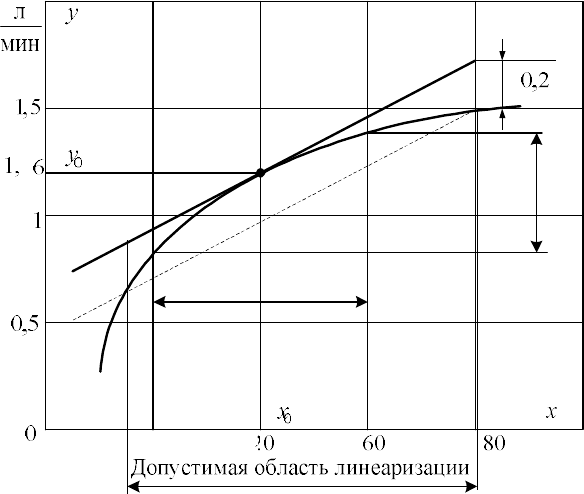
Пример 2.13. Линеаризация характеристики вентиля. Требу-
ется линеаризовать нелинейную характеристику вентиля (рис. 2.17)
в окрестности рабочей точки при положении клапана
0
xx
= 40%
таким образом, чтобы допустимая погрешность линеаризации не
превышала ±0,2 л/мин.
Коэффициент передачи вентиля
%минл/014,0
%
40
л/мин56,0
л
в
x
y
k .
Линеаризованная характеристика (касательная) на рис. 2.17
описывается уравнением
93
)(
0в0
xxkyy
при
л
yy
.
Штриховая линия, параллельная касательной и соответствую-
щая разности y - y
л
= 0,2 л/мин, задает максимальную ошибку и оп-
ределяет допустимую область линейного приближения.
Пример 2.14. Линеаризация нелинейной характеристики гене-
ратора.
Уравнение генератора имеет вид
,9,0
u
где
u
- выходное напряжение;
- потокосцепление;
Ω – скорость;
0,9 - коэффициент пропорциональности.
x
y
Рис. 2.17. Линеаризация характеристики вентиля
94
Требуется линеаризовать характеристику генератора в окрест-
ности рабочей точки
0
= 20 В·с/рад; Ω
0
= 25 рад/с;
u
0
= 450 В. По-
грешность линеаризации не должна превышать 5% от величины
0
u , т.е.
0
uu 22 В.
Определим частные производные от
u
по
и Ω:
5,22;9,0
0
uu
рад/с;
18;9,0
0
uu
В∙с/рад.
Уравнение линеаризованной характеристики генератора при
u
0
= 450 В имеет вид
2518205,22
00000
uu
uu .
Погрешности линеаризации приближенно оценим с помощью
отброшенных членов ряда Тейлора, соответствующих вторым про-
изводным от нелинейной функции:
.)())((2
)(
2
1
2
00
2
2
000
2
2
00
2
2
л
uu
u
uuu
Вторые частные производные равны:
.0;9,0;0
2
22
2
2
uuu
Таким образом:
))((9,0
00
u .
Для обеспечения заданной погрешности линеаризации должно
выполняться условие
.22))((9,0
00
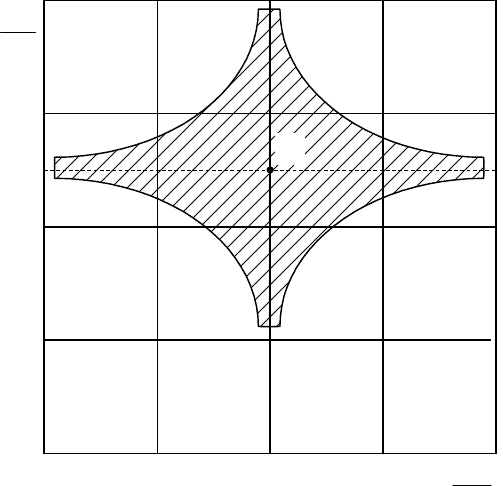
Соответствующая этому условию допустимая область линеари-
зации показана на рис. 2.18.
95
Контрольные вопросы и упражнения
1. Объясните сущность и дайте сравнительный анализ эквива-
лентных и неэквивалентных преобразований аналитических моде-
лей.
20
10
0
10 20 30
с
рад
30
рад
сВ
ψ
A
Рис. 2.18. Допустимая область линеаризации (к примеру 2.14)
2. От чего зависит погрешность линеаризации нелинейной ха-
рактеристики системы?
3. Как зависят характеристики линеаризованной системы от
координат рабочей точки и почему?
4. Объясните содержание методов теории размерности при по-
строении моделей систем.
5. Объем газового пузыря, образовавшегося в результате глу-
бинного подводного взрыва, колеблется с периодом, пропорцио-

96
нальным
cba
Ep . Здесь
p
- давление,
- плотность воды,
E
-
полная энергия взрыва. Определите cba ,, .
6. На сферу, движущуюся в жидкости, действует сила, завися-
щая от радиуса сферы
r
, скорости движения
v
и вязкости
. Со-
ставьте уравнение, моделирующее зависимость силы от указанных
величин. Размерность вязкости -
11
смкг
.
7. В колебательной системе возвращающая сила и коэффици-
ент вязкого трения убывают со временем. Дифференциальное урав-
нение имеет вид
0
2
t
x
t
x
x
.
Составьте модель системы в виде структурной схемы. Определите
характер колебаний в системе.
8. Грузик массой m на пружинке с жесткостью
c
совершает ко-
лебания в жидкости. Составьте математическую модель колебатель-
ной системы. Определите, при каком значении коэффициента вяз-
кого трения
грузик без колебаний движется к положению равно-
весия?
9. Простейшим уравнением, описывающим нелинейные коле-
бания, является уравнение Дюффинга
0
32
xxx
.
Составьте математическую модель колебательной системы. Оп-
ределите при 0
период малых колебаний. При каком значении
энергии период стремится к бесконечности?
10. Запишите дифференциальные уравнения для механических
систем, изображенных на рис. 2.18. На чертеже обозначено:
1
c ,
2
c -
жесткости пружин;
1
,
2
- коэффициенты, моделирующие демп-
фирование в системе;
1
x ,
2
x - перемещения. Предполагается, что
внешние силы отсутствуют, а системы приходят в движение только
за счет начальных условий. Составьте структурные схемы динами-
ческих систем.
11. На рис. 2.20 изображена механическая система с враща-
тельным движением в жидкой среде. К внешнему цилиндру с мо-
ментом инерции
1
J приложен вращающий момент
M
. Через вяз-
кое трение с коэффициентом
1
движение передается телу с момен-
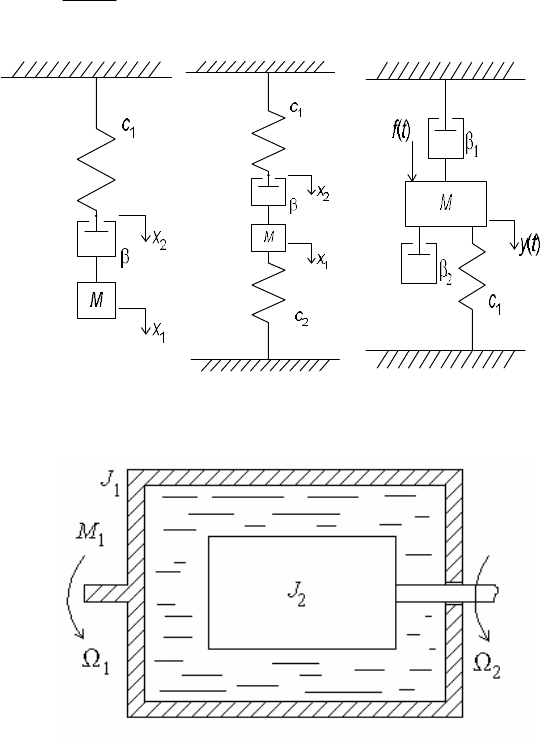
97
том инерции
2
J . Запишите дифференциальные уравнения для этой
системы. Определите передаточную функцию
sM
s
sH
2
.
Рис. 2.19. Механические колебательные системы
Рис. 2.20. Механическая система (к задаче 7)
12. Дано дифференциальное уравнение
0
xfx
. Линеари-
зуйте его в окрестности точки
0
x
. Функция
xf имеет вид:
2
xxf ;
3
xxf ;
x
exf
.

98
3. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ
ДИНАМИЧЕСКИХ СИСТЕМ
3.1. Вычислительные методы расчетов
при моделировании систем
При моделировании динамических систем на цифровых ЭВМ
используются цифровые модели, от способа построения которых
зависит как точность получаемых результатов, так и объем вычис-
лительных затрат. В задачах анализа и синтеза автоматических
систем используются различные методы перехода от непрерывных
моделей в виде взаимосвязанных линейных и нелинейных интегро-
дифференциальных и алгебраических уравнений, функциональ-
ных и логарифмических зависимостей вида
0,,
tvyf
d
;
0,,
tvyf
s
,
где
d
f и
d
f - заданные интегро-дифференциальные и алгеб-
раические уравнения и функциональные зависимости; y - вектор
координат системы; v - вектор внешних воздействий, к дискретным
моделям вида
0,,
tvyF
d
.
Простейший способ дискретной аппроксимации заключается в
замене в исходных уравнениях дифференциалов разностями. На-
пример, для левых разностей имеем соотношения
;
1
h
yy
t
y
dt
dy
iii
2
21
2
1
2
2
2
2
2
h
yy
y
h
yy
t
y
dt
yd
ii
i
iii
,
и т.д., где h - шаг.
Такая алгебраизация дифференциальных уравнений приводит
к разностным уравнениям, для решения которых необходимы на-
чальные значения решения, определение которых возможно только
с помощью других методов. В случае представления дифференци-
ального уравнения в нормальной форме Коши

99
tvyfy ,,
,
решения в точках
i
t
и
1i
t связаны интегральным уравнением
dttyftydyftyty
iii
i
tt
iii
t
t
ii
11
0
1
,, .
С использованием одного из методов приближенного вычисле-
ния интегралa можно получить соответствующую дискретную мо-
дель. Однако при таком подходе свойства дискретной модели могут
существенно отличаться от свойств исходной системы. Рассмотрим,
например, модель в виде дифференциального уравнения первого
порядка
.
00
ubyay
(3.1)
При использовании одной из схем численного интегрирования
Адамса-Башфорта
,),(,3
3
111
iiiiii
tyftyf
h
yy
прямой подстановкой можно получить разностное уравнение
,3
222
3
1
0
1
0
01
iiiii
uu
hb
y
ha
ya
h
y (3.2)
которому соответствует импульсная передаточная функция
22
3
13
2
0
0
2
0
ha
za
h
z
z
hb
zu
zy
zH
.
Таким образом, исходному дифференциальному уравнению
(3.1) с одним полюсом ставится в соответствие разностное урав-
нение (3.2) с двумя полюсами. Полюсу в комплексной плоскости
0
ap
соответствует полюс в z-плоскости
phz exp
. Общее
решение разностного уравнения (3.2) будет иметь две составляю-
щие, определяемые двумя корнями, в отличие от общего решения
исходного дифференциального уравнения, имеющего одну состав-
ляющую, и ни один из корней характеристического уравнения для

100
разностного уравнения не будет точно совпадать с корнем характе-
ристического уравнения исходной модели при любых значениях h.
Из примера следует, что использование схем численного интег-
рирования для построения дискретных моделей приводит к появле-
нию дополнительных составляющих в решении, величина которых
зависит от шага интегрирования h. Поэтому при использовании
численных методов необходимо иметь оценку погрешности для вы-
бора шага h.
В случае представления исходной математической модели в
виде передаточной функции по Лапласу
sH для получения дис-
кретной модели могут быть использованы таблицы
z-преобразований. По известной импульсной передаточной функ-
ции можно записать разностное уравнение согласно известным со-
отношениям и теореме о сдвиге.
Приближенный метод получения дискретной модели без ис-
пользования таблиц z-преобразований основан на использовании
соотношений Тастина. Он состоит в том, что в передаточной функ-
ции оператор s заменяется первым членом разложения в ряд функ-
ции
.
)1(3
1
1
12
ln
1
3
3
z
z
z
z
h
z
h
При использовании оператора Тастина можно получить дис-
кретные модели, эффективные только для малых h, поскольку при-
менение оператора Тастина эквивалентно многократному интегри-
рованию по явному методу Эйлера.
Другой способ построения дискретно-аналоговых моделей ди-
намических систем состоит в том, чтобы аппроксимировать не всю
правую часть уравнения
tuyf ,, или решения
ty , а только вход-
ную координату
tu полиномом различного порядка на каждом из
подынтервалов
1
,
ii
tt и с помощью операторных методов полу-
чить решение и разностное уравнение. Схема такой дискретной ап-
проксимации приведена на рис. 3.1. Непрерывный сигнал
tu пре-
образуется в последовательность дискретных значений решетчатой
функции
ihu
, которая затем аппроксимируется преобразователем
