Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем
Подождите немного. Документ загружается.

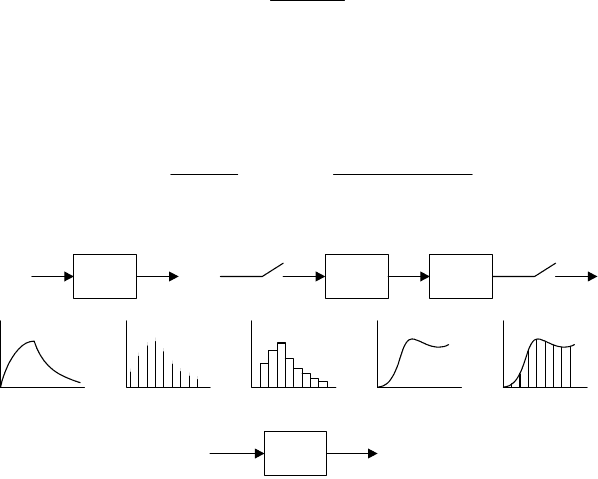
101
в непрерывную )(
~
tu . Затем выходная координата непрерывной час-
ти y(t) вновь аппроксимируется в решетчатую функцию
ihy . Точ-
ность такого моделирования для произвольного вида
tu определя-
ется типом преобразователя решетчатой функции
ihu в непрерыв-
ную )(
~
tu . Преимущественное использование имеют экстраполяция
на интервале
1
,
ii
tt нулевого порядка (прямоугольная)
hiuihutu )1()()(
~
и первого порядка (зубцами)
).()(
~
1
i
ii
i
tt
h
uu
utu
Передаточные функции экстраполяторов нулевого и первого
порядков равны соответственно
;
1
)(
0
s
e
sH
sh
э
2
2
1
11
)(
hs
ehs
sH
sh
э
.
Рис. 3.1. Схема дискретной аппроксимации динамического блока
при цифровом моделировании
Таким образом, для конкретного типового блока с передаточ-
ной функцией
sH с учетом экстраполятора импульсов передаточ-
ную функцию можно представить в виде
)
(
s
H
)
(
t
u
)
(
t
y
)(
1
sH
)
(
s
H
)
(
s
u
)
(
z
u
)
(
~
s
u
)
(
~
s
y
)
(
z
y
)
(
t
u
)(
*
ihu
)
(
~
t
u
)
(
~
t
y
)
(
ih
y
t
t
t
t
t
0 0 0 00
)
(
z
H
)
(
z
U
)
(
z
Y

102
)()(
)(
)(
)( sHsHZ
ihu
ihy
zzH
1
э
. (3.3)
Обратное z-преобразование для (3.3) дает разностное (рекур-
рентное) уравнение для цифрового моделирования типового дина-
мического элемента. Полученные таким образом разностные урав-
нения экстраполируют входные воздействия на каждом шаге и, сле-
довательно, являются явными. Их порядок точности составляет со-
ответственно O(h) и O(h
2
). Важной их особенностью является то,
что они точно аппроксимируют свободную составляющую решения.
При интерполяции входного воздействия на интервале
1
,
ii
tt по-
лучаются неявные разностные схемы, которые в общем случае об-
ладают более высокими точностью и устойчивостью.
Рассмотрим линейный динамический элемент (рис. 3.1) с од-
ним входом и одним выходом и передаточной функцией
,
)(
)(
)(
sA
sB
sH
где
m
i
n
i
in
i
im
i
sasAsbsB
0=
=)(
0
.)(;
Точное решение для выходного сигнала на шаге интегрирова-
ния
1
,
ii
tt можно получить с помощью операторных методов, если
известны начальные условия и точная аппроксимация входного
воздействия на этом интервале. В этом случае
,
)(
)(
)(
)(
)()()(
sA
sA
sA
sB
sUsHsY
нн
(3.4)
где
...)0()0()0()(
2
110
1
0
mm
sububsubsB
н
;)0(...)0()0(
1
)2(
1
)1(
0
ububub
m
mm
;

103
...)0()0()0()(
2
110
1
0
nn
syayasyasA
н
;)0(...)0()0(
1
)2(
1
)1(
0
yayaya
n
nn
;
)0(u , )0(u
и т.д. - начальные значения (при t = 0 + ;
0)
входного сигнала и его производных;
)0(y , )0(y
и т.д. - начальные значения (при t = 0 + ; 0)
выходной координаты и ее производных.
Для перехода во временную область необходимо аппроксими-
ровать входное воздействие на интервале
1
,
ii
tt и определить его
изображение. При этом если экстраполировать входное воздейст-
вие, то в результате обратного преобразования получается явная
схема, если интегрировать - неявная.
Для интерполяции входного воздействия можно использовать
сплайны различных порядков: нулевого, первого, второго и др.
Наиболее рациональным является использование линейных сплай-
нов, для которых
.)(
1
i
ii
i
tt
h
uu
utu
(3.5)
Изображение входного воздействия вида (3.5) описывается вы-
ражением
.
2
1
)(
1
2
h
uu
s
s
u
sU
iii
(3.6)
Подставив (3.6) в выражение для изображения выходного сиг-
нала (3.4), получим
.
)(
)(
)(
)(
2
)()(
2
1
sA
sA
sA
sB
hs
uu
s
u
sHsY
iii нн
(3.7)
Для конкретных типовых линейных звеньев, подставляя соот-
ветствующие выражения в (3.7), можно получить алгоритмы моде-
лирования в виде неявных разностных уравнений.

104
3.2. Моделирование типовых блоков динамических систем
Большинство элементов сложных динамических систем могут
быть представлены в виде линейных звеньев первого или второго
порядка. Рассмотрим алгоритмы составления дискретных моделей
основных блоков динамических систем.
Динамические звенья первого порядка
Дифференциальное уравнение первого порядка представим в
общем виде
.
0101
bubyaya
Решение этого уравнения на шаге интегрирования
1
,
ii
tt при
аппроксимации входного воздействия на этом интервале линейным
сплайном (3.5) и при известных начальных условиях в области изо-
бражений Лапласа имеет вид
.
2
)(
01
1
01
1
2
1
11
01
ii
iii
y
asa
a
u
asa
b
hs
uu
s
u
asa
bsb
sY
(3.8)
Применение обратного преобразования Лапласа к уравнению
(3.8) для конкретных динамических звеньев позволяет получить со-
ответствующие алгоритмы моделирования в виде неявных разност-
ных уравнений
,
11 iiii
uuyy
(3.9)
где
,
и
– рекуррентные коэффициенты.
Для типовых блоков первого порядка рекуррентные коэффици-
енты приведены в табл. 3.1.
Разностные уравнения для интегрирующего и изодромного
звеньев, получающиеся на основе рекуррентных коэффициентов,
приведенных в табл. 3.1, соответствуют разностным уравнениям
неявного метода Адамса - Маултона второго (неявный метод Эйле-

105
ра) и третьего порядков. Они не являются жестко устойчивыми (об-
ладающими устойчивостью и сохраняющими точность в широком
диапазоне изменения шага расчета), поэтому для моделирования
таких типовых блоков целесообразно использовать разностные схе-
мы методов численного интегрирования Гира.
Для остальных типовых блоков разностные уравнения второго
и третьего порядков являются А–устойчивыми и точно воспроизво-
дят свободную составляющую решений исходных дифференциаль-
ных уравнений. А-устойчивыми называют вычислительные мето-
ды, обладающие вычислительной устойчивостью при любом соот-
ношении величины шага расчета h и постоянных времени системы.
Таблица 3.1
Рекуррентные коэффициенты для типовых динамических
блоков первого порядка
sH
Ts
1
1
T
h
T
h
2
1
Ts
k
T
h
e
hTT
h
k
hTT
h
k
Ts
0
h
T
h
T
1
Ts
ks
T
h
e
1
h
k
1
h
k
1
Tsk
0
hT
h
k
h
kT
sT
sTk
2
1
1
1
hT
T
k
2
2
2
2
hT
T
k
1
2
2
2
1
1
2
1
sT
sTk
T
h
e
hTT
h
k
21
1
hTT
h
k
21
1
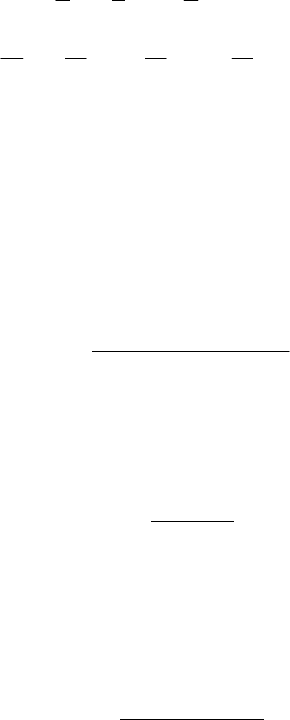
106
Методы Гира k-го порядка являются k-шаговыми и жестко ус-
тойчивыми. Формулы методов Гира первого, второго и третьего
порядков имеют вид соответственно
111
,
iiii
tyhfyy ;
1111
,
3
2
3
1
3
4
iiiii
tyhfyyy ;
11211
,
11
6
11
2
11
9
11
18
iiniii
tyhfyyyy .
Динамические звенья второго порядка
При моделировании непрерывных динамических объектов,
описываемых дифференциальными уравнениями второго порядка,
возможны три случая.
Корни характеристического уравнения комплексно-
сопряженные, и передаточная функция имеет вид
.
1
1
)(
2222
1
1
TTssT
sT
sH
Корни мнимые и сопряженные, модель описывается передаточ-
ной функцией:
.
1
)1(
)(
22
2
1
2
sT
sTk
sH
Корни действительные, передаточная функция объекта эквива-
лентна передаточной функции двух последовательно соединенных
звеньев первого порядка:
.
)1)(1(
)1(
)(
32
1
3
sTsT
sTk
sH
Используя рассмотренный выше подход, можно получить ре-
куррентную формулу (при линейной аппроксимации входного воз-
действия блока)

107
iiiii
uuuyy
,
111
.
Значения рекуррентных коэффициентов для всех рассмотренных
случаев приведены в табл. 3.2.
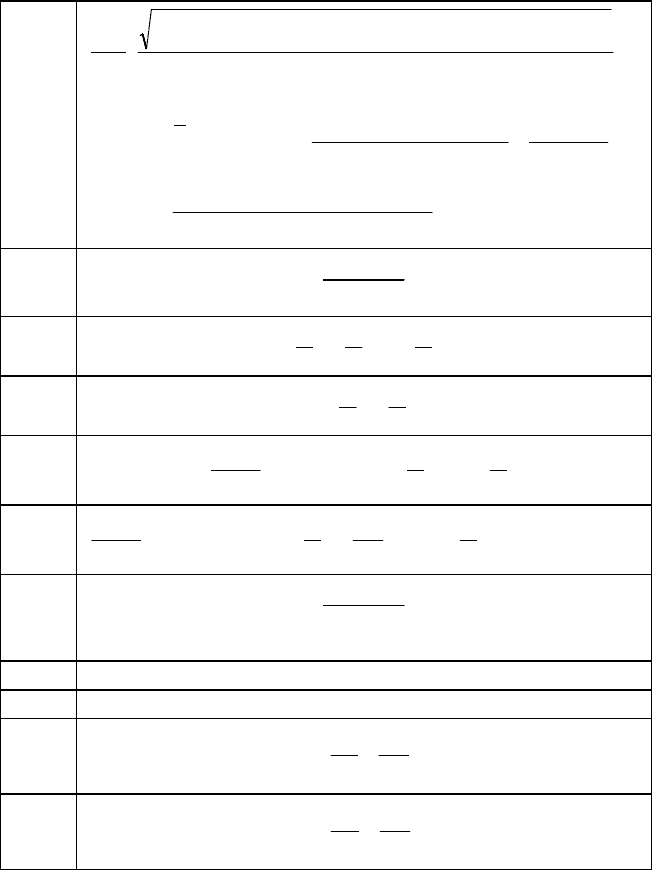
Таблица 3.2
Рекуррентные коэффициенты для динамических блоков
второго порядка
sH
1
12
2
TssT
k
h
T
h
h
sinexp
1
;
2
1
1
T
T
h
hThTTh
h
kT
expcos2sin2
2
22
T
h
h
T
T
h
h
expsin
1
sin
1
22
Tarctg
T
h
eh
T
T
h
h
TT
h
Th
kT
cos
2
sin
2
2
2
2
2
3
2
sH
2
222
1
12
1
TTssT
sTk
T
h
eh
T
T
h
h
Tarctg
sin
1
sin
1
22
he
h
T
h
sin
1
2
22
22
11
22
222
1
2
1
1
2
1
2
)sin(
)1(
T
TTTT
he
TT
TTTT
hT
kT
T
h
22
1 T
h
;
)(2
1
1
T
TT
TT
arctgarctg
108
Окончание табл. 3.2
)1(
21
22
1
2
11
22
2
2
1
22
1
1
2
TTT
TThThTTTTThTThT
hT
kT
222
22
22
1
1
1
12
)sin(
T
h
T
ThTT
he
T
h
;
T
TTThTThT
TThThTT
-arctgarctg 2
1
2
2
1
22
1
11
sH
3
1
1
22
2
1
sT
sTk
T
h
T
h
h
T
cossin
T
h
h
T
sin
T
h
T
T
h
ThT
hT
Tk
sincos
11
1
22
T
h
T
T
hT
T
h
hTT
hT
Tk
sincos
1
11
1
22
sH
4
22
1
1
sT
sTk
2
-1
T
hT
T
h
k
23
1
2
T
hT
T
h
k
26
1
2
109
Блоки с переменными параметрами
При моделировании сложных систем часто требуется исследо-
вать процессы при изменениях параметров со скоростями, соизме-
римыми со скоростями основных переходных процессов. Возможны
два способа учета изменений параметров объектов.
При первом способе объекты с переменными параметрами рас-
сматривают как сложную систему, по полному описанию которой
формируют подробную структурную схему из простейших блоков.
Любое изменение параметра выражается в виде дифференциальных
уравнений или функциональных соотношений. В результате вычис-
ляемые переменные параметры через блоки перемножения связы-
ваются с элементами структурной схемы основной расчетной моде-
ли объекта исследования.
Рассмотренный подход используется, как правило, в тех случа-
ях, когда переменные параметры являются объектом исследования,
т.е. имеется необходимость их наблюдения, измерения, оптимиза-
ции и др.
При втором способе динамический объект с переменными пара-
метрами представляют в виде
,)()()()(
0101
utbutbytayta
(3.10)
где )(),( tbta
jj
- зависимости параметров от времени.
При структурном моделировании сложных систем целесообразно
использовать дискретные модели для типовых блоков, описывае-
мых уравнениями вида (3.10). Получить разностные уравнения для
типовых блоков с переменными параметрами с помощью преобра-
зований Лапласа затруднительно вследствие наличия в уравнении
(3.10) произведений функций от независимой переменной.
Для решения такой задачи целесообразно использовать тео-
рию дифференциальных преобразований (преобразований Тейло-
ра). Условием применения преобразований Тейлора является воз-
можность представления функций-оригиналов на шаге расчета
степенными рядами. Тейлоровское изображение U(k) функции-
оригинала u(τ) определяется выражением

110
,,0,
)(
!
)(
0
k
u
k
H
kU
k
kk
τ
(3.11)
где H – произвольная постоянная преобразований;
k – целочисленный аргумент.
Обратное преобразование
0
)()(
k
k
H
kUu
(3.12)
является разложением функции
u в ряд Тейлора.
Применив к исходному дифференциальному уравнению ти-
пового блока на интервале расчета
1
,
ii
tt прямое преобразование
Тейлора (3.11) и выбрав масштабную функцию, определим дискре-
ты спектра )()( tykY
выходной координаты блока. В момент
htt
ii
1
значение выходной координаты
1i
y типового блока
может выражаться через дискреты
0
1
),(
k
ii
kYy
(3.13)
где индекс-дискрет указывает номер шага расчета.
Введение обозначения операции получения Т-производной
)(
))...(2)(1(
)( nkY
k
nkkk
kYD
n
n
позволяет по аналогии с записью дифференциального уравнения
первого порядка с постоянными параметрами в области изображе-
ний Лапласа
)()(
01
01
sU
asa
bsb
sY
записать соответствующее уравнение в области изображений Тей-
лора
)()(
01
01
kU
aDa
bDb
kY
