Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем

111

или

).()()()(

0101

kUbkDUbkYakDYa







(3.14)

Выражение (3.14) позволяет непосредственно перейти к раз-

ностному уравнению для моделирования типового динамического

блока. Уравнение для интервала расчета





1

,

ii

tt имеет вид

.)()()1(

)1(

001

1

















 kYakUbkU

h

k

b

ak

h

kY

iiii

(3.15)

В соответствии с (3.15) уравнение для реакции блока можно

записать в виде суммы дискрет Y

i

(k):











0

1

)1(

k

iii

kYyy

. (3.16)

Дифференциальное уравнение первого порядка с переменны-

ми параметрами (3.10) с учетом правила преобразования Тейлора







k

i

kVUtvtu

0

)()()()( 

для интервала





1

,

ii

tt принимает вид

 

.)()()1(

)1(

)(

)()()1(

1(

)(

0

01

0

01







































k

i

ii

k

i

ii

kUBkU

h

k

B

kYAkY

h

k

A









(3.17)

Определение значений дискрет Y

i

(k) из уравнения (3.17) тре-

бует аппроксимации на подынтервале





1

,

ii

tt входной координаты





tu и переменных параметров





ta

j

,





tb

j

. Для этого можно вос-

пользоваться, например, линейным сплайном.

В этом случае, продифференцировав уравнение (3.5) k раз и

подставив результат в соотношение (3.11) с учетом соответствия

нулевой дискреты значению функции-оригинала, получим

(3.18)

.0)(...)2(

);()1(;)0(

1









LUU

uuUuU

ii

iiiii

112

Учитывая, что

ii

yY



)0( , из уравнения (3.18) получим значе-

ния дискрет ,0),1(  kkY

i

:

 

































).1()(

..........................................................

;)2(00

2

)3(

;)1()(0

2

)2(

;)()1(

1

0

1

1010

001

1



ii

iii

iiii

Y

a

h

Y

Ya

a

h

Y

Yauub

h

Y

yaubuu

h

b

a

h

Y



(3.19)

Аналогичным образом получаются соотношения для вычис-

ления дискрет других динамических блоков первого порядка с пе-

ременным параметром )()( tTta

i



(табл. 3.3). Эти соотношения

справедливы при любом номере шага.

Недостаток разностной схемы (3.16) – большие вычислитель-

ные затраты, связанные с вычислением на каждом шаге L значения

)1(



kY

i

. Процедуру вычислений можно упростить, если в общем

виде просуммировать значения дискрет для типовых блоков. В

формуле (3.16) вторая и последующая дискреты в правой части оп-

ределяются через известные значения предыдущих дискрет. Подста-

вив их последовательно в общем виде и просуммировав в соответ-

ствии с (3.16), определим неявную разностную схему в случае ин-

терполяции линейным сплайном

),1(

)(

2

1

11

















kY

k

T

TT

uuyy

k

i

ii

iiiiiii





где

iii







,, - рекуррентные коэффициенты для типовых блоков с

постоянными параметрами при

i

tt



.

113

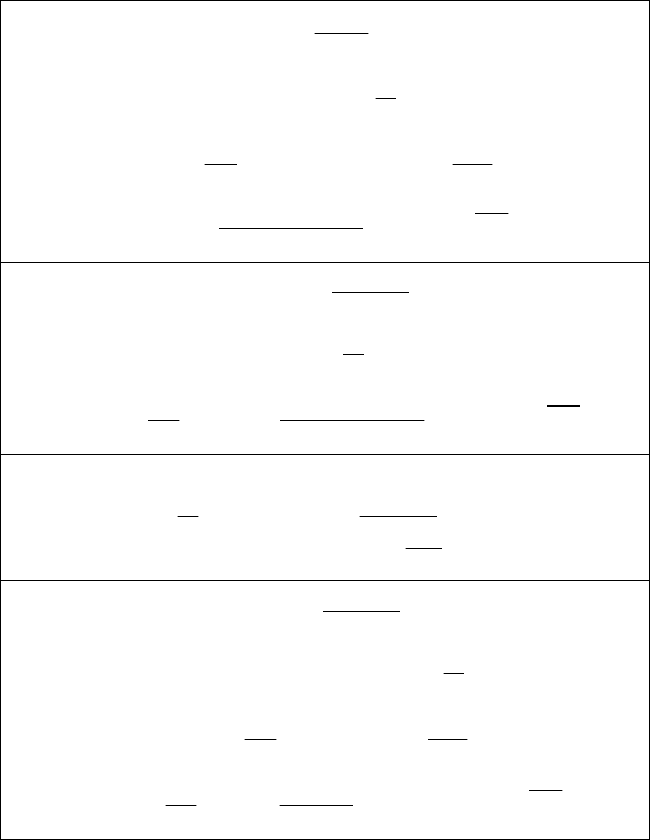
Таблица 3.3

Т-дискреты для типовых динамических блоков первого

порядка с переменными параметрами

stT

tsH

)(

1

),( 

;

;)1(;)0(

1 i

i

u

T

h

YyY 

;

)1(

)()(

2

)2(

11

















h

Y

TTuu

T

h

Y

iiii

i









,3),1(

))(1(

)(

1

kkY

T

TTk

kY

i

ii

;

1)(

),(





stT

k

tsH

);()1(;)0(

ii

i

yku

T

h

YyY 























,3,)1(

))(1(

)1()(

1

kkY

h

TTk

kY

kT

h

kY

ii

i

;)(),( stTtsH



);()1();()0(

1

1 ii

ii

i

uu

h

TT

Yuu

h

T

Y 







.,3,0)(;0)2(  kkYY

;

1)(

),(





stT

kTs

tsH

;)()1(;)0(

11 i

i

iii

y

T

h

uukTYyY 



;

)1(

()1(

2

)2(

1

















h

Y

TTY

T

h

Y

ii

i























,3,)1()1()1()(

1

kkYk

h

TT

kY

kT

h

kY

ii

i

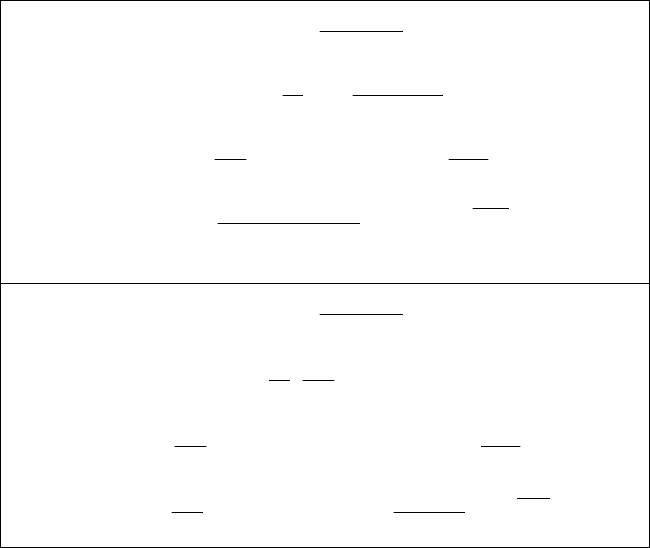
114

Окончание табл. 3.3

;

)(

)1(

),(

2

1

stT

sTk

tsH





];

)(

[)1(;0)0(

1

1 i

ii

y

i

ku

h

uu

Tk

T

h

YY 







;

)1(

)()(

2

)2(

11

h

Y

TTuu

T

kh

Y

iiii

i





.,3),1(

))(1(

)(

1









kkY

kT

TTk

kY

i

ii

;

)(

)1(

),(

2

1

stT

sTk

tsH





;)()1(;)0(

1















 iiiii

ykuuu

h

kT

T

h

YyY

;

)1(

)()1()(

2

)2(

11

















h

Y

TTYuuk

T

h

Y

iiii

i





















,3,

)1(

)()1()(

1

k

h

kY

TTkY

kT

h

kY

ii

i

.

3.3. Имитационное моделирование систем, представленных

уравнениями с частными производными

Многие динамические системы, например, объекты с распреде-

ленными параметрами, описываются дифференциальными уравне-

ниями в частных производных или их комбинациями с обыкновен-

ными дифференциальными уравнениями и алгебраическими соот-

ношениями. Для моделирования таких систем разработан ряд мето-

дов, простейший из которых основан на непосредственной фор-

мальной аппроксимации. Рассмотрим сущность этого метода на

примере численного решения первой краевой задачи на отрезке [0,

l

] для уравнения теплопроводности

115

   

       



































.,;,0

;0,,0

;0,0,

21

0

tutlututu

lxxuxu

Ttlx

x

u

xt

u

(3.20)

Решение краевой задачи (определения решения дифференци-

ального уравнения второго порядка при двух заданных условиях в

двух разных, но не соседних точках) предполагается существующим

в области

lx



0

,

Tt





0

.

Введем на плоскости ),( tx равномерную сетку с шагом по про-

странству

N

l

h  и шагом по времени

M

T

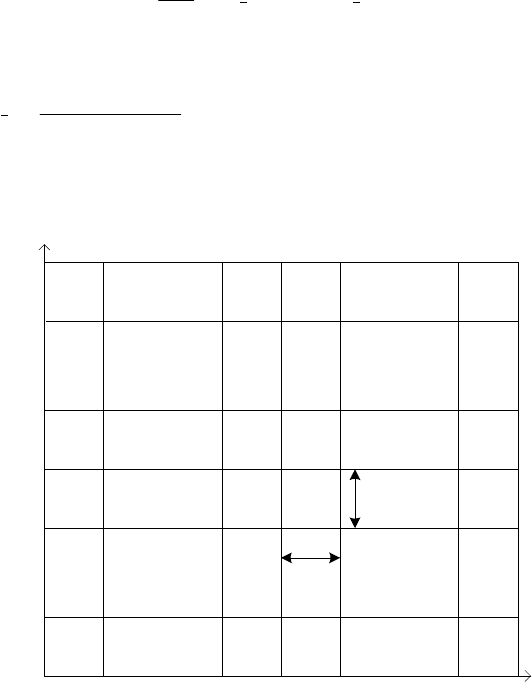
 , как показано на рис.

3.2. Точки пересечения горизонтальных и вертикальных линий об-

разуют множество узлов сетки

τh

w , совокупность узлов с одинако-

выми индексами

j

представляет собой временной слой (рис. 3.2).

В граничных узлах функция





txu , известна из краевых условий

(3.20). При этом аппроксимация решения для этих узлов имеет вид:





j

tuy

1

0

 ;





j

N

tuy

2

 , Mj ,...,1,0



;





ii

xuy

0

 ,

Ni



0

.

Задача, таким образом, сводится к определению значений

j

i

y

на множестве внутренних узлов сетки

τh

w . Выполним аппроксима-

цию дискретного оператора разностным, записывая его одинаковым

образом в любой точке





j

i

tx , сетки

τh

w . Заменим производную по

времени первой разностью









 j

i

j

i

yy

t

u

1

.

Так как в последнем выражении участвуют значения разност-

ного решения с двух временных слоев, вторую производную по

x

заменим суммой приближенных решений, взятых на





1



j - ом и

j

-ом слоях:

116

 

j

xx

j

xx

yy

x

u







1

2

,

где

10





;

2

11

2

h

yyy

y

iii

xx







 ;

1

,...,

2

,

1





N

i

,

10

uy



,

2

uy

N



.



h

0

1

x

1i

x

i

x

1i

x

1N

x

l

1

t

1j

t

j

t

1



j

t

1



M

t

T

j

i

,

rh

w

,

x

t

Рис. 3.2. Дискретизация расчетной области с помощью

равномерной сетки

Таким образом (3.20) преобразуется в схему с весами

117

 

   

 





































.0,

;,...,0,,,,0

;,

;

2

1

2

0

21

0

2

11

2

1

11

1

Nixuy

Mjtluytuy

wyx

h

yyy

h

yyy

yy

ii

jj

N

jj

h

j

i

j

i

j

i

j

i

j

i

j

i

j

i

j

i

j

i







(3.21)

Полученная система





1



MN линейных алгебраических урав-

нений позволяет вычислить столько же значений функции

j

i

y . Ка-

ждое из уравнений (3.21) записано при

0





на шеститочечном

шаблоне с использованием узлов с индексами

























jijijijiyjji ,1,,,,1,1,1,1,,1,1









. Погреш-

ность аппроксимации в общем случае есть величина первого поряд-

ка по времени и второго порядка по пространству





2

hO  . Для

симметричной схемы с

5

,

0





порядок аппроксимации увеличива-

ется до





2

O .

При

0





каждое из уравнений системы (3.21) содержит только

одну неизвестную величину

1j

i

y . В этом случае решение легко на-

ходится по явным формулам при переходе от

j

-го слоя к )1(



j -

му слою с использованием известных значений решения на границе

(слой

j

=0).

При неявной схеме и

0





разностные уравнения содержат три

неизвестных величины:

1





j

i

y ,

1j

i

y ,

1



j

i

y . Их определение осущест-

вляется путем решения трехточечной задачи вида

iiiiiii

FyByCyA









 11

,

1

,...,

1





N

i

. (3.22)

Решение (3.22) выполняется методом прогонки. Сущность этого

метода заключается в следующем. Предполагается, что решение

(3.22) имеет рекуррентную форму

111 





iiii

yy





, (3.23)

118

подстановка которой в (3.22) дает для коэффициентов

1i



и

1i



рекуррентные соотношения

iii

i

AC

B







1

;

iii

i

AC

FA











1

;

1

,...,

1





N

i

.

С помощью последних уравнений и краевого условия при

0



i

находятся

1i



,

1i



во всех узлах сетки (прямая прогонка). Затем

по известным

1i



,

1i



с помощью формулы (3.23) и условия в

точке

Ni



вычисляются значения

N

y ,

1N

y , …,

1

y ,

0

y (обратная

прогонка).

Аналогичным образом формируются разностные схемы типа

(3.21) для других краевых задач.

3.4. Примеры имитационного моделирования

автоматических систем

При цифровом моделировании автоматической системы по

структурной схеме необходимо однозначно определить каждый

элемент моделируемой системы, указать входные и выходные пере-

менные каждого блока, задать связи блоков друг с другом, указать

начальные условия для динамических элементов, выбрать шаг рас-

чета. Обычно шаг расчета выбирают из соотношения h = 0,1

min{T

j

}, где {T

j

} - множество постоянных времени динамических

блоков расчетной структурной схемы и периодов внешних воздей-

ствий.

Пример 3.1. Электрический двигатель постоянного тока.

Структурная схема двигателя постоянного тока независимого

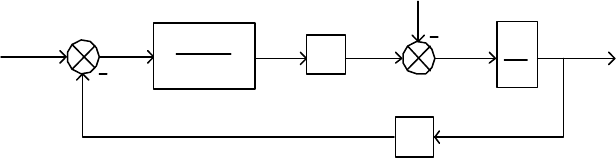
возбуждения показана на рис. 2.13. На рис. 3.3 приведена соответ-

ствующая ей схема для структурного моделирования, где указаны

обозначения переменных всех блоков, использованные при состав-

лении программы.

Для переменных на входах и выходах динамических блоков

введены следующие обозначения: EZs, IDs, EMs, WDs («старые»

значения, вычисленные на предыдущем шаге) и EZn, IDn, EMn,

WDn («новые» значения, полученные для текущего шага).

119

C

Uz

sLR 

1

Js

1

C

ID

Ez

MD

EM

WD

Mc



Рис. 3.3. Схема для моделирования двигателя постоянного тока

В конце каждого цикла расчета выполняется присвоение пе-

ременных EZs = EZn, IDs = IDn , EMs = EMn, WDs = WDn.

Пуск двигателя моделируется при 0



с

M . При t = EndTime/2

момент нагрузки на валу двигателя увеличивается на величину

с

M .

Вариант программы на языке Power Basic для моделирования

двигателя показан ниже.

Программа для моделирования двигателя

постоянного тока

screen 12 'VGA 640x480

key (10) on: on key (10) gosub 10

'ПАРАМЕТРЫ ДВИГАТЕЛЯ

R

=1 'Ом, активное сопротивление

якорной обмотки

C=0.553 'конструктивная постоянная

двигателя С

L = 0.015 'Индуктивность якорной обмотки

Jd = 0.01125 'Момент инерции вращающихся

масс

Uz = 110 'Напряжение на якорной обмотке

Mc = 5 'Момент нагрузки

'ПАРАМЕТРЫ МОДЕЛИРОВАНИЯ

EndTime = 0.5 'Время моделирования

dTime = 0.0001 'Шаг моделирования

120

'ВСПОМОГАТЕЛЬНЫЕ ПЕРЕМЕННЫЕ

Kp = 1/R

Tp = L/R

Gamma = exp(-dTime/Tp)

'НАСТРОЙКИ ЭКРАНА ДЛЯ ОТОБРАЖЕНИЯ ГРАФИКОВ

view(100,50)-(400,350),7,1

window(0,-0.5*Uz)-(EndTime,2*Uz)

'СЕТКА

FOR i=-0.5*Uz TO 2*Uz STEP 0.4*Uz

Line(0,i)-(EndTime,i),1

NEXt i

FOR i=0 TO EndTime STEP 0.2*EndTime

Line(i,-0.5*Uz)-(i,2*Uz),1

NEXT i

'ПОДПИСИ под графиком

Locate 24,13: ? "0";: ? space$(36);: ?

EndTime"c."

'ЦИКЛ МОДЕЛИРОВАНИЯ

'Инициализация старых значений переменных

EZs = 0 ' EZ – Разность напряжения и противоЭДС

(на выходе элемента сравнения)

IDS = 0 ' ID - Ток якорной обмотки

WDs = 0 ' WD - Угловая скорость двигателя

EMs = 0 ' EM - Суммарный момент на валу

FOR Time = dTime TO EndTime STEP dTime

'Текущая разность напряжения и противоЭДС

EZn = Uz - WDs*C

'Апериодическое звено (ток якорной обмотки)

dEZ = (EZn - EZs)/dTime

IDn = IDs*Gamma+Kp*(1-

Gamma)*EZs+Kp*(Tp*Gamma+dTime-Tp)*dEZ

'Электромагнитный момент двигателя

MD = C*IDn

'Разность электромагнитного момента и момента

нагрузки

IF Time > EndTime/2 THEN EMn = MD - Mc ELSE

EMn = MD

'Интегратор (угловая скорость)

Малафеев С.И., Малафеева А.А. Моделирование и расчет автоматических систем

Подождите немного. Документ загружается.