Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

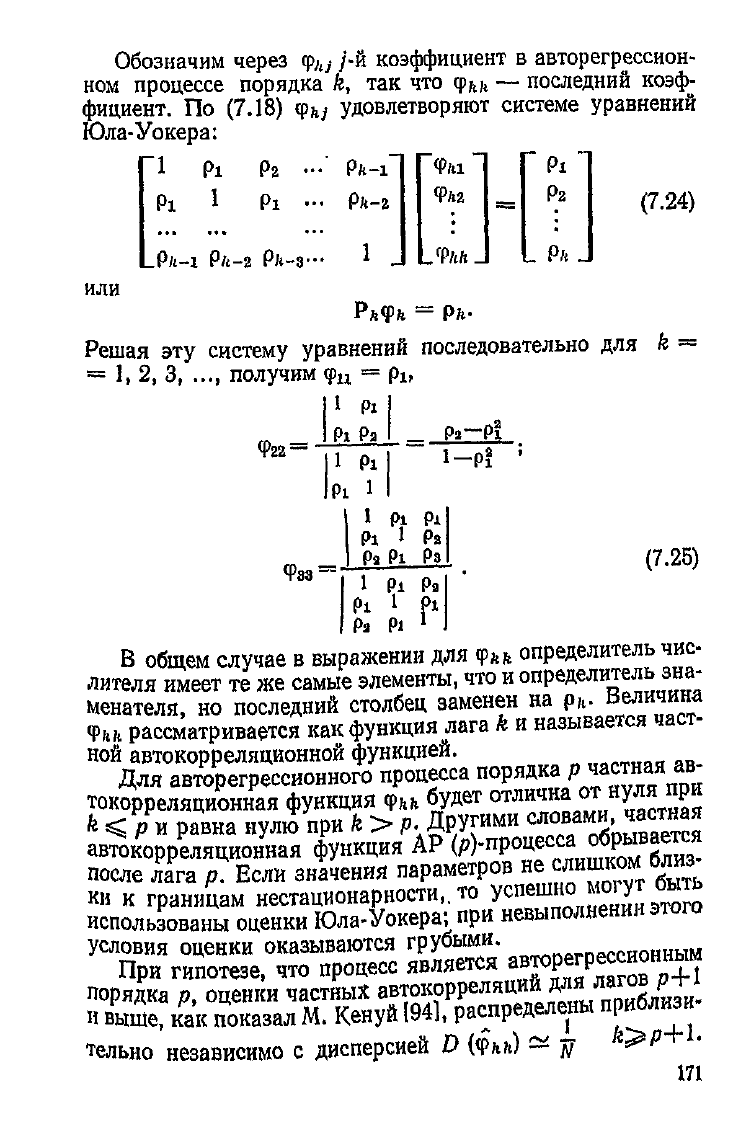
Обозначим через

j-ik

коэффициент

авторегрессион-

ном

процессе порядка

fe, так что

cp^t

—

последний

коэф-

фициент.

По

(7.18)

cpbj

удовлетворяют системе уравнений

Юла-Уокера:

(7.24)

(7.25)

В общем

случае

выражении для cp

ftft

определитель чис-

лителя имеет

те

же самые элементы, что и определитель зна-

менателя,

но

последний столбец заменен

на p

Вел

™

<Pfc

рассматривается как функция лага

и называется част-

ной

автокорреляционной функцией.

„„„,„,.

а яп

Для авторегрессионного процесса порядка Р «сгнм ав-

токорреляционная

функция

будет

отлична

от

нуля при

< р и

равна нулю при

k >

р. Другими

™°*

$™*™

автокорреляционная

функция

АР

(Р>^

от

™™каиблю-

после лага

р.

Если значения параметров не

«иш«^

кв

границам нестационарности,,

то

сп&ш

^^21вт^о

использованы оценки Юла-Уокера; при невыполнении этого

условия оценки оказываются грубыми.

шм

При

гипотезе,

что

процесс является ^тоР

гре^иоиным

порядка

р,

оценки частных автокорреляций дляi лагов p+i

выше, как показал М. Кенуй [94], распределены приблизи

тельно независимо

дисперсией

(<рьь)

& jf ^

171

или

Решая

эту

систему уравнений последовательно

для k =

2, 3, ...,

получим фи

= pi,

Таким образом, стандартная ошибка оцененной частной

автокорреляции ф^

будет:

(7.26)

Это и

служит

критерием определения момента обрыва

функции.

Частная автокорреляционная функция

существует

также

для процессов скользящего среднего. Как мы уже видели

(7.13), модель СС(1) эквивалентна модели АР с бесконечным

числом членов. Это означает, что частная автокорреляцион-

ная

функция в данном

случае

будет

убывать бесконечно, но

обрыва иметь не

будет.

Это свойство имеет более общий ха-

рактер и присуще моделям СС высоких порядков, а также

процессам АРСС.

Рассмотренные свойства моделей сведены в табл. 7.1.

Здесь наглядно видны взаимно-обратные свойства СС и АР-

процессов.

Таблица

7.1

Свойства

автокорреляционных

функций

\,Процесс

Функция

^ч-

Рл

ФА*.

ÄP

(р)

бесконечная

убывающая

.обрыв после

лага

СС

(<?)

обрыв после

лага

бесконечная

убывающая'

АРСС (Р, Ч)

бесконечная, после

первых {q—р) ла-

гов доминирует

наложение

затуха-

ющих экспонент и

синусоид

бесконечная, после

первых (р—q) ла*

гов доминирует на-

ложение

затуха-

ющих экспонент и

синусоид

§ 2.

ИДЕНТИФИКАЦИЯ

МОДЕЛЕЙ.

ИНТЕРПРЕТАЦИЯ R

В МОДЕЛЯХ АРСС

Теперь у нас достаточно информации для того,

чтобы перейти к проблемам построения, оценки и использо-

вания

моделей прогнозирования.

172

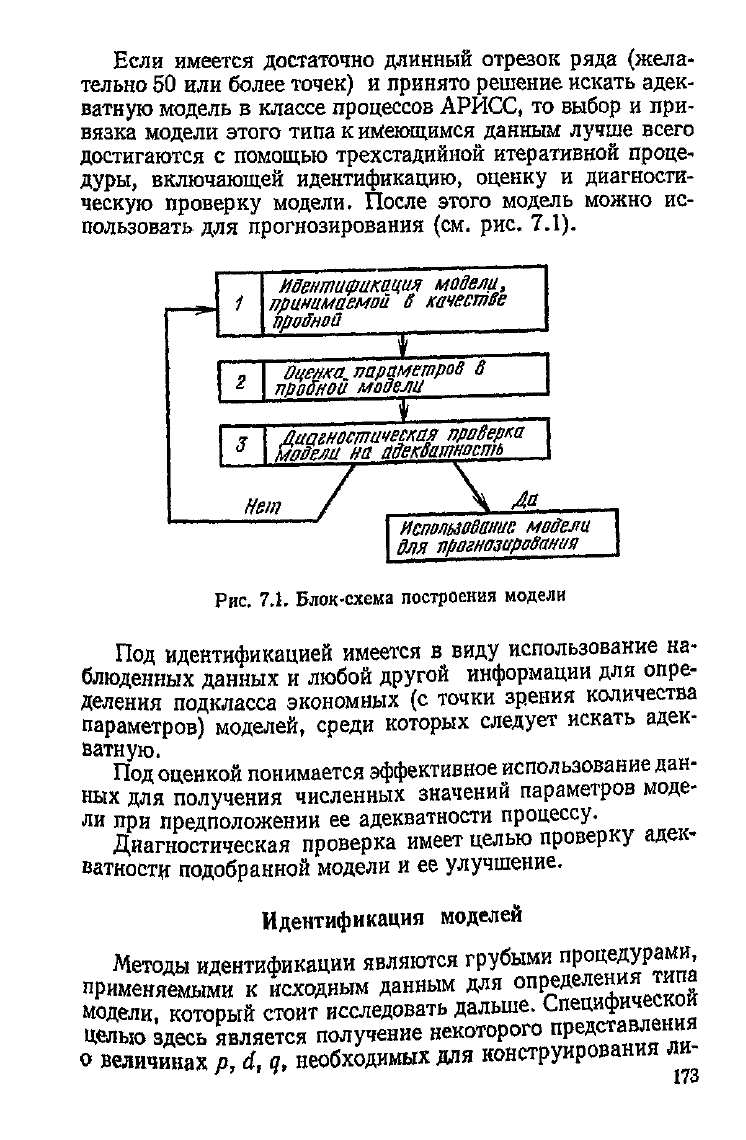
Если имеется достаточно длинный отрезок ряда (жела-

тельно 50 или более точек) и принято решение искать адек-

ватную модель в классе процессов АРИСС, то выбор и при-

вязка

модели этого типа к имеющимся данным

лучше

всего

достигаются с помощью трехстадийной итеративной проце-

дуры,

включающей идентификацию, оценку и диагности-

ческую проверку модели. После этого модель можно ис-

пользовать для прогнозирования (см. рис. 7.1).

Рис.

7.L

Блок-схема построения модели

Под

идентификацией имеется в

виду

использование на-

блюденных данных и любой

другой

информации для опре-

деления подкласса экономных (с точки зрения количества

параметров) моделей, среди которых

следует

искать адек-

ватную.

Под

оценкой

понимается

эффективное

использование дан-

ных для получения численных значений параметров моде-

ли при предположении ее адекватности процессу.

Диагностическая проверка имеет целью проверку адек-

ватности подобранной модели и ее улучшение.

Идентификация

моделей

Методы идентификации являются грубыми процедурами,

применяемыми

к исходным данным для определения типа

модели, который стоит исследовать дальше.

Спе

«^ескоя

Целью здесь является получение некоторого предетавления

величинах р, d, q, необходимых для конструирования ли-

173

нейной

модели АРИСС (р, d, q) и получение предваритель-

ных оценок ее параметров. Идентификация распадается на

две стадии.

1. Определение порядка разности d исходного ряда х,

который обеспечивает стационарность.

2. Идентификация модели АРСС для ряда

Главными инструментами анализа на обеих стадиях яв-

ляются автокорреляционная и частная автокорреляционная

функции.

Они используются

не

только для определения вида

модели, но и для приближенной оценки параметров.

Идентификацияпорядка

разности rf.

Мы

видели, что для стационарного смешанного процесса

автокорреляционная

функция удовлетворяет разностному

уравнению ф (В)рь = 0, k

>•

q — p.

Решение

этого уравнения для fe-й автокорреляции

(в

предположении, что корни характеристического уравне-

ния

различны) имеет вид:

(7.27)

Условие стационарности,

требующее

чтобы нули поли-

нома

,Ф

{В) лежали вне единичного круга, означает, что

Gj,

, ..., G

лежат внутри единичного круга. Из

(7.27)

яс-

но,

что в

случае

стационарного процесса, для которого ни

один из корней не лежит близко к границе единичного кру-

га, автокорреляционная функция

будет

сравнительно быст-

ро

затухать

с ростом k. Если же один вещественный корень,

скажем G

, близок к 1, так что G

= 1 — Ö, где б является

некоторой малой положительной величиной, то для боль-

шого k

автокорреляционная

функция

будет

затухать

медленно и

почти линейно. Это свойство используется в качестве инди-

катора корня, близкого к 1.

Способность автокорреляционной функции сохранять по-

стоянное

значение с ростом k может означать, что нужно

рассматривать исследуемый процесс как

нестационарный,

но

возможно, что его разность при этом стационарна. Отметим,

что оцененные корреляции не обязательно должны быть

очень высоки.

По

изложенным причинам предполагается, что порядок

разности d

обеспечивающий стационарность, достигнут тог-

да, когда автокорреляционная функция процесса w

—

=У% падает довольно быстро. На практике обычно d =

1,2, и, как правило, достаточно проанализировать пер-

вые

15—20

значений автокорреляционной функции исход-

ного ряда и его первых и вторых разностей.

Идентификация

процесса S7

. Опре-

делив экспериментально d, изучаем затем общий вид оце-

ненной

автокорреляционной и частной автокорреляцион-

ной

функций для разностей порядка d. На их основе выби-

раются р

q для АР

СС

операторов. Для этого используют-

ся

рассмотренные выше свойства (см. табл. 7.1). Кроме то-

го, в работе [54] показано, что теоретически возможный мак-

симум коэффициентов автокорреляции для процесса CC{q)

определяется соотношениями:

В частности, р

(max) ~ cos \^Щ-

Особое практическое значение имеют АР и ОС-процес-

сы 1-го и 2-го порядков и простейший смешанный процесс

(1,

1), Для моделей этих процессов имеют место законо-

мерности и соотношения, сведенные в табл. 7.2.

Мы видим, что предварительные оценки параметров для

моделей (0, d 1) и (1, d, 1) находят решая квадратические

уравнения, значит, формально

будет

получено по два реше-

ния.

Однако лишь одно из каждой пары решении

будет

в,oq-

ласти допустимых значений, определяемой

спот

™

™*

ционарности и обратимости. Из оставшихся

случаев

лишь

(О,

2) представляет трудность. Для этого процесса прно-

лиженные оценки,параметров находят итеративно

следую-

щим образом. ,„_

от«

Имея

оценки автоковариаций и соотношения (1.Ы).

а б л

ц а 7.2

Основные свойства и соотношения

для наиболее важных моделей АРИСС

Модель

Поведение рл

Поведение

cpuk

Предваритель-

ные оценки

Допустимая

область

Модель

Поведение рл

Поведение ФАЛ

Предваритель-

ные оценки

Область допу-

стимых значе-

ний

Модель

Поведение рл

(1,

d, 0)

убывает экспоненциаль-

но

ТОЛЬКО

фцт^О

— 1<ф1 <1

(2,

d, 0)

наложение затухающих

экспонент и синусоид

ТОЛЬКО

фц=)Ь0

ф22=Й

«Р1= \-г\

—

1<ф

Ф2

Ф1 <1

—фх <1

(0, rf, 1)

только

pi=£0

доминирует экспонен-

циальное затухание

— 1<QI<1

(0,

d, 2)

ТОЛЬКО

Pl^=0,

р2=#°

доминирует наложение

затухающих экспонент

синусоид

—1 «За <1

—Qi<l

(1.

а, 1)

Экспоненциально убывает, начиная с

176

Продолжение

можно подсчитать- последовательно

указанном порядке

оценки

параметров

ст|, Q

-v

•••>&. используя

ите-

рацию:

при

условии что On

= 0.

Для начала итерации параметры

•Ü

приравниваются нулю. В частности, для про-

цесса (0,

2) уравнения имеют вид:

При

получении оценок, конечно, необходимо сверяться

с областью допустимых значении.

177

Модель

Поведение

фьь

Предваритель-

ные оценки

Область

допу-

стимых

значе-

ний

(1.

d, 1)

Начиная с ft = l,

доминирует

затухающая

экспонента

(l-Öi Фх) (<Р1-&)..

r r

Q2 _

ф1 ,Qi

Интерпретация

моделях АРСС

Для анализа моделей авторегрессии и скользящего сред-

него также можно ввести статистику

как это делается

множественной регрессии

(7.28)

где

а%

—

дисперсия белого шума;

D (х)

—

дисперсия временного ряда.

Величина

изменяется

от 0 до I и

представляет собой

относительную меру определенности Прогноза, получае-

мого

на

основе прошлой информации.

работе Ч. Нельсо-

на

188]

показано,

как R

связан

автокорреляциями

вре-

менного ряда

характеристиками генерирующего процес-

са. Большое внимание уделено интерпретации R

. Эта вели-

чина может быть особенно полезна при построении модели

на

стадии

идентификации,

когда

ее

предварительная оценку

дает

исследователю представление

прогнозируемости вре-

менного ряда

помогает избежать дальнейшего бесполез-

ного поиска лучших моделей, повышающих

Рассмотрим временной,

ряд х

генерируемый моделью

авторегрессии

—

скользящего среднего:

где

—

фиксированные параметры, удовлетворяющие

условиям стационарности

обратимости соответственно,

—

белый

шум.

Этот процесс может быть записан

обращенном виде как

процесс скользящего среднего бесконечного порядка:

гдё

^ являются функциями от

<fo

и Qi и

(7.29)

Далее, в § 3, показано, что дисперсия ошибки прогноза по мо-

дели АРСС на 1 шаг вперед равна о*.

178

результате

подстановки

(7.29)

(7.28)

получаем

(7.30)

Таким

образом,

не зависит от

а!.

Подсчет величины

R* по формул^

(7.30)

на стадии идентификации затрудните-

лен.

Поэтому, учитывая, что веса

определяют автокорре

ляционную функцию временного ряда,

°°f

зать R

коэффициентами

автокорреляции. Проще всего это

сделать для чистых авторегрессионных процессов.

Обозначая автоковар^иации процесса

™-

J25f

лом

получаем, что дисперсия

определяется выраже

нйем:

Так

что, обозначая

для AP-процесса порядка

через

Rp,

имеем:

где

—

вектор-столбец (pi,

•••»

РР),

Чр

—

вектор-столбец

(cpi,

•••. Ф^

•

Юла-Уокера

Далее, используя оценки параметров

1ила

(см.

7.19)

где Р,

автокорреляшю»ная

<>%££*,£&

функцию

одних лишь коэффициентов

лы rv

(Ри

....

PJJ):

(7.31)

В частности,

для

процесса АР

(1)

179

для процесса АР(2)

Возможен еще один альтернативный способ выражения

, который с точки зрения интерпретации особенно поле-

зен.

Рассмотрим долю дисперсии х

которая может быть

объяснена регрессией x

на x

-i, затем регрессией на

_ i и x

_ г, потом на x

, x

-z и x

и т, д.

Если опять обозначить R

, характеризующий эти по-

следовательные регрессии через R?, RJ, R1 и т. д., то из

теории линейной регрессии

следует,

что

(7.32)

где

qijf

— коэффициент частной автокорреляции.

Это выражение означает, что дополнительный вклад в

при последовательном добавлении новой лаговой объяс-

няющей

переменной определяется коэффициентом частной

автокорреляции для данного лага, который показывает, ка-

кая

доля необъясненной до этого дисперсии x

теперь полу-

чает

объяснение. Становится понятным, почему R* для про-

цесса АР(р) зависит только от (р

1г

..., р_р). Это объясняется

тем, что ф/у = 0 для / > р, а также тем, что, как это

следует

из

уравнений Юла-Уокера, частные автокорреляции до ла-

га р включительно зависят только от (р

..., р

На

практике можно считать, что добавление новых лаго-

вых объясняющих переменных (увеличение порядка эмпи-

рической модели)

даст

малый вклад в R

, если выборочные

оценки

частных автокорреляций для этих лагов малы.

Анализ R

для моделей чистого скользящего среднего

CC(q)

легко проводить, если известны параметры Q, так как веса

% в

(7.30)

в этом

случае

равны коэффициентам &:

(7.33)

183