Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

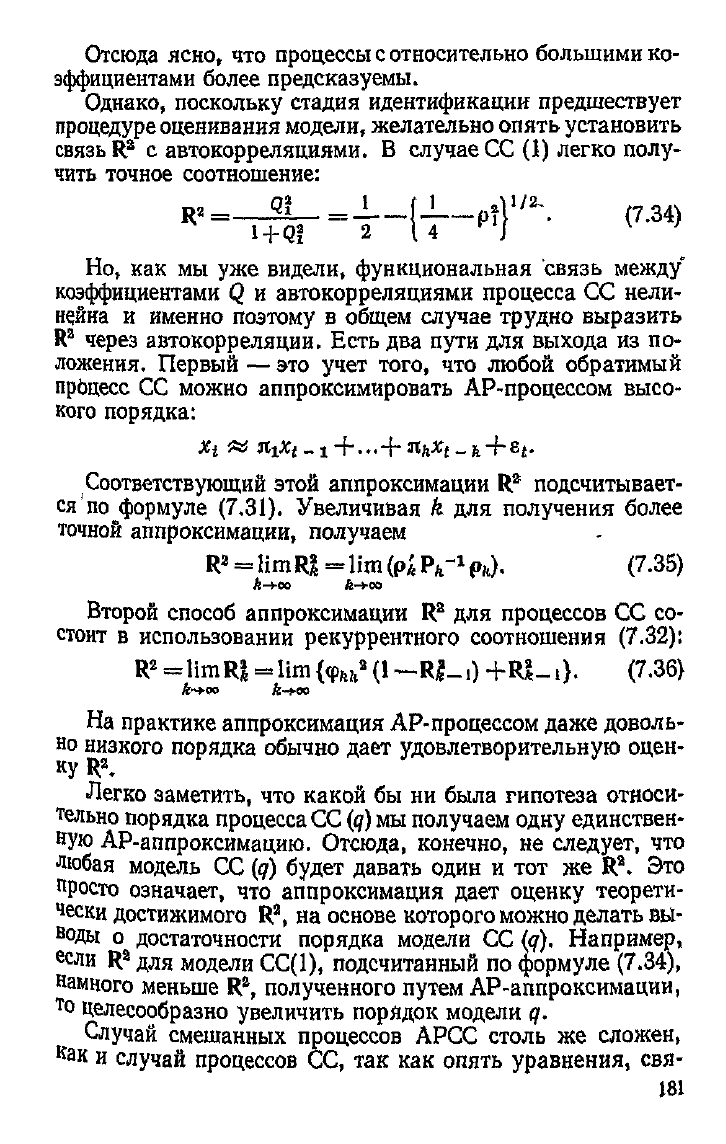
Отсюда

ясно,

что процессы с относительно большими ко-

эффициентами

более предсказуемы.

Однако,

поскольку стадия идентификации предшествует

процедуре

оценивания

модели, желательно опять установить

связь

R* с автокорреляциями. В

случае

СС

(1) легко полу-

чить точное соотношение:

(7.34)

Но,

как мы уже видели, функциональная связь

между

коэффициентами

Q и автокорреляциями процесса СС нели-

нейна

и именно поэтому в общем

случае

трудно выразить

через автокорреляции. Есть два пути для

выхода

из по-

ложения.

Первый — это

учет

того, что любой обратимый

процесс СС можно аппроксимировать AP-процессом высо-

кого порядка:

Соответствующий этой аппроксимации R

подсчитывает-

ся'по

формуле (7.31). Увеличивая k для получения более

точной аппроксимации, получаем

(7.35)

Второй способ аппроксимации R

для процессов СС со-

стоит в использовании рекуррентного соотношения (7.32):

(7.36)

На

практике аппроксимация AP-процессом

даже

доволь-

но

низкого порядка обычно

дает

удовлетворительную оцен-

ку R

Легко заметить, что какой бы ни была гипотеза относи-

тельно порядка процесса

СС (q)

мы получаем одну единствен-

ную AP-аппроксимацию. Отсюда, конечно, не

следует,

что

любая модель СС (?)

будет

давать один и тот же R

. Это

просто означает, что аппроксимация

дает

оценку теорети-

чески достижимого R

, на основе которого можно делать вы-

воды о достаточности порядка модели СС (q). Например,

сли R

для модели СС(1), подсчитанный по формуле (7.34),

намного меньше R

, полученного путем АР-аппроксимации,

о Целесообразно увеличить порядок модели q.

Случай смешанных процессов АРСС столь же сложен,

ак

и случай процессов СС, так как опять уравнения, свя-

181

зывающие параметры с автокорреляциями,

нелинейны.

Здесь

также используются оценки R

по формулам

(7.35)

или

(7.36).

В заключение еще раз подчеркнем, что оценки автокор-

реляций,

лежащих в основе процедуры идентификации, мо-

гут иметь довольно большие дисперсии и быть сильно авто-

коррелированными.

Поэтой причине нет строгого соответст-

вия

между

теоретической и

оцененной

автокорреляционными

функциями.

Это приводит к затруднениям при выборе р,

на данной стадии

могут

быть выбраны две или несколько

различных моделей для дальнейшего исследования. На этой

стадии особенно полезны графические методы, опыт самого

исследователя. В сомнительных

случаях

может быть целе-

сообразней использовать нестационарную модель, чем стаци-

онарную, ибо она является более гибкой. Выбор пробных

моделей на этой стадии — отправной пункт для примене-

ния

более формальных и

эффективных

методов оценивания.

§ 3. ОЦЕНИВАНИЕ МОДЕЛЕЙ

И ПРОГНОЗИРОВАНИЕ

На

стадии идентификации были получены

грубые

оценки

параметров модели, теперь необходимо получить

такие оценки параметров, которые приводят к наиболее точ-

ным

прогнозам.

Предположим,что находимся в точке t и должны сделать

прогноз х

(f) величины xt+%. Пусть для получения про-

гноза используется линейная комбинация бесконечного чис-

ла значений &

, ... — реализаций белого шума к мо-

менту t. Допустим далее, что наилучший прогноз может быть

представлен в виде

где .веса орх,

1|5т+ь

•••

должны быть определены. Тогда,

учитывая,

что*/+

= 2 ^-и-Л средний квадрат ошиб-

ки

прогноза равен:

182

Он

достигает минимума при "фт-н/

i't+/.

Таким обра-

зом,

значение прогнозируемого члена ряда можно пред-

ставить в виде

двух

групп слагаемых:

где

(7.37)

есть ошибка прогноза

(t).

Ошибка прогноза на

шаг вперед

будет

Как

видим, ошибка прогнозирования на один шаг впе-

ред оказывается равной значению белого шума, генерирую-

щего процесс в следующий момент времени. И следователь-

но,

дисперсия белого шума

будет

также дисперсией ошибки

прогнозов на один шаг вперед.

Самый простой и наглядный способ получения модели

с минимальным средним квадратом ошибки прогноза — это

графическое изучение Ее? суммы квадратов расхождений

между

реальными членами ряда и их прогнозами, сделан-

ными

на предыдущем шаге, в зависимости от значении пара-

метров, задаваемых в окрестности их предварительных оце-

нок.

Минимум этой суммы

будет

определять искомые зна*

чения

параметров. При условии нормальности распределе-

ния

множества значений е эти оценки

будут

совпадать с

оценками,

полученными по

методу

максимума правдоподо-

бия.

Существуют

другие

способы поиска оценок парамет-

ров.

Например, алгоритм Марквардта для нелинейного ме-

тода,

наименьших квадратов. Различные модификации этого

алгоритма можно найти в [74] и в [5]. Рассмотрим лишь

один из способов оценивания, предложенный Боксом и

Дженкинсом.

Общая модель может быть записана как' e

Q-

(В)Ф (B)w

где w

#f,

щ = w

— ix».

Необходимо минимизировать 2е?.

183

Пусть ß =

(<р,

0) — вектор параметров модели, а ß

=(фо»

Qo)—вектор их предварительных оценок. Рассматри-

вая

каждое значение e

как

функцию

от ß, можно разложить

ei в ряд Тейлора около его значения s

, соответствующего

вектору предварительных оценок параметров ß

(7.38)

где

Если

начальные значения в, v, и положить равными ну-

лю, то остальные

могут

быть подсчитаны рекурсивно сле-

дующим образом:

В соответствии с

(7.38)

получаем приближенное уравне-

ние

линейной регрессии

(7.39)

котором e

играет роль остатка. Тогда корректировками

параметров, минимизирующих 2е*, оказываются

коэффи-

циенты

регрессии

ti0

на «*_,/ и

„

Добавляя к°Р"

ректировки

к первым приближенным оценкам (q>

, Qo)>

п0

лучаем

набор вторых приближений, которые во второй ите-

рации

заменяют вектор ß

. Итерация проводится до тех

пор»

пока

не

будет

достигнута сходимость.

184

Поскольку итеративный цикл начинается с нулевых зна-

чений

е, v, и, то несколько их первых значений

будут

грубы-

ми, они

отбрасываются и не используются в уравнении (7.39).

Из

этого уравнения легко получить частные случаи для раз-

личных рад.

При

построении модели

следует

проанализировать нет

ли параметрической избыточности, нельзя ли упростить

структуру.

Наличие избыточности не

всегда

очевидно. На-

пример,

общий множитель слева и справа в модели

можно

увидеть

только после выделения множителей в левой

части

т.е.

Модель с параметрической избыточностью создает серьез-

ные трудности в процедуре оценивания. На практике

труд-

ности создают не только случаи точного сокращения, но и

близкие к этому. Оценки при этом

будут

нестабильными

из-за почти одинаковых множителей в обеих частях модели.

В табл. 7.3 приведены ковариационные матрицы оценок

параметров для моделей, представляющих особый прак-

тический интерес.

Таблица

7.3

Ковариационные

матрицы

оценок

параметров

некоторых

моделей

(n=N — а)

Процесс

АР(1)

АР

(2)

СС(1)

СС(2)

АРСС

(1,1)

Ковариационная матрица

V(q>)=n-4l~<P

)

V(Q) =n~

(l-Q

)

РхО+фа)]

1—Ф1

V(Q

)

'[ _

Ql(1H

Qa) x

„r

'h\

1-Ф<Э[(1-Ф

)(1-Ф(г)

(1-Ф»)

(1—Q^i

185

Из

табл. 7.3 видно, что при

ц>

= Q дисперсии оценок

<р

Q в модели АРСС (1,1) бесконечны. Это и есть случай со-

кращающихся множителей АР и СС-частей.

Диагностическая проверка модели на адекватность

Одним из способов проверки является построение моде-

ли несколько более

общей,

чем та, которая считается истин-

ной,

и сравнение этих моделей, выявление незначимых

параметров. Данный метод предполагает, что можно опре-

делить слабое звено в модели, из-за которого она оказалась

неадекватна. Однако сделать это довольно затруднительно,

особенно когда выборка невелика. Более формальная про-

верка основана на анализе автокорреляционной функций

остатков. Рассмотрим ее.

Анализ остатков. Если' бы модель была адек-

ватна исследуемому процессу, то e

были бы нёкоррёлиро-

ваны

и.оценки

(k)

распределены приблизительно нормаль-

но

около нуля с дисперсией, равной гг

, или соответствен-

но

со стандартной

ошибкой

п *. В нашем

случае

п —

N—d,<

где N — число наблюдений в выборке, ad — порядок раз-

ности.

Это положение можно использовать для приближен-

ной

оценки статистической значимости отклонений оценок

этих автокорреляций от нуля. Однако Дж. Дарбин 156] пре-

достерегает

от недооценки статистической

значимости

откло-

нений

автокорреляций r

(k)

от их теоретических

нулевых

значений,

если при малых

лагах

k исходить из стандартной

ошибки

. Он, например, показал, что для процесса

АР (1) с параметром

<р

дисперсия г

(1) есть <p

ft-\ а это

мо-

жет быть существенно

меньше

чем пг

. Кроме

случаев

срав-

нительно больших лагов, п~^

следует

рассматривать как

верхнюю границу стандартных ошибок для r

(k).

Помимо

индивидуального анализа коэффициентов г

{Щ

возможен

общий

совокупный

тест

автокорреляционной

фун

ции

остатков. При этом задаются целью выяснить не свиде-

тельствуют

ли первые, скажем, 20 автокорреляций остат-

ков,

взятые вместе, о неадекватности модели.

Пусть имеется К оценок автокорреляций

180

Тогда можно показать [45], что если построенная модель

адекватна временному

ряду,

то случайная величина

распределена как %

(/(—р — q). Если же модель не соответ-

ствует

временному

ряду,

автокорреляции остатков

будут

существенными, а величина © большой. Таким образом, об-

щую проверку гипотезы об адекватности модели можно осу-

ществить

путем

сопоставления © с таблицей у? с

(К—р—ф-

степенями свободы.

Неадекватность модели может иметь место из-за измене-

ний

значений параметров во времени при сохранении формы

модели. Для выявления этой особенности проделывается

следующая операция. Исследуемый отрезок данных разби-

вается на два и к каждому привязывается модель.

Пометим параметры моделей для каждой из половин отрез-

ка

соответствующими индексами Ql

\(p^\

ср}

а)

.Им

со-

ответствуют

стандартные ошибки оценок 0QI

\ OQV",

Ф/>

Оф*

}

Отсюда

находим, что стандартные ошибки разно-

стей

Сопоставляя разности параметров с их стандартными

ошибками,

можно

сделать

вывод

вероятности действитель-

ного изменения параметров. Если такие изменения имели

место, то

берутся

оценки параметров, полученные на основе

более свежих данных.

Использование

д л я проверки ста-

тистических гипотез. Опыт

свидетельствует

том, что часто уже после оценивания нескольких альтерна-

тивных моделей исследователь оказывается в затруднении,

не

зная,

какой модели

отдать

предпочтение. На этой стадии

Целесообразно получить уточненные оценки R

, которые

работе Ч. Нельсона [88] предложено использовать для

проверки статистических гипотез. Для этого разработана

асимптотическая теория, основывающаяся на анализе от-

ношения

правдоподобий.

Пусть р означает вектор (ф

, .... <р

; Q

.... Q

), aß,—

вектор подмножества элементов вектора ß. Часто исследо-

187

вателя интересует проверка гипотезы того, что все элементы,

равны нулю, т. е. что соответствующие s параметров не

нужно включать в модель. В более общем виде можно рас-

смотреть гипотезу вида

(7.40)

где ßs —

специфицированный

набор значений s параметров.

Обозначим

максимальное^

значение

функции правдоподо-

бия

для вектора ß через L (ß), а для вектора ß

, на который

наложены ограничения (7.40), — через L (ß

). Отношение

) к L (ß) показывает, насколько хорошо гипотеза

(7,40)

соответствует

данным.

Проверка гипотезы может быть ocrio-

вана

на том факте, что для больших выборок статистика

(7.41)

распределена как %

с s-степенями свободы. Если гипотеза

неверна,

то

Ä,

принимает большое значение, и в этом

случае

гипотеза

(7.40)

отвергается.

Легко показать, что в

случае

нормального закона рас-

пределения

(7.41)

сводится к

где z

(ß) — остаток, подсчитанный для момента

как

функ-

ция

параметров $,

Выборочная оценка Я

,для модели без наложения огра-

ничений

на параметры определяется как

а для модели с наложенными ограничениями

таким

образом, статистический критерий принимает вид

все еще зависящий от неизвестного параметра аЦ. Если

вместо с! подставить оценку гг

2е

* ф), где п = N

—'

188

— число наблюдений, то получим выражение

, удобное

для вычислений:

(7.42)

Статистика к определяется относительным увеличением R

результате

устранения ограничений на параметры. Если

увеличение большое, то гипотеза

(7.40)

отвергается.

Теория распределений

является асимптотической. Меж-

ду тем на практике часто имеется очень немного данных для

получения выборочной оценки

а%.

В связи с этим по анало-

гии с соответствующей ситуацией в линейной регрессии,

для которой разработана теория малой выборки, предла-

гается также, несколько видоизмененная статистика:

(7.43)

где

F имеет ^-распределение es

и (п

— р — q —1)-степенями

свободы (одна степень свободы вычтена в предположении, что

константа определена). Распределения F пу?

будут

давать

практически одинаковые результаты, если (п — р — q — 1)

порядка ста или выше. Об адекватности

двух

статистик при

выборках обычного для практики объема ничего неизвестно.

В частном

случае,

когда s = 1, F превращается в ^-рас-

пределение с (n—p — q— 1)-степенями свободы.

На

практике часто выдвигается гипотеза ß = 0, т. е.

что

все (р + q) параметров равны нулю. В этом

случае

n[RV(l-R2

)

]

i так какК

Итак,

имея оценки R

, можно вычислить значения F или

и, сопоставив их с табличными значениями, отвергнуть

или

принять проверяемую гипотезу.

При

сравнении моделей возможны ошибки

двух

видов,

ьо-первых, может быть

отвергнута

модель с меньшим чис-

лом параметров, которая на самом

деле

адекватна

ряду,

принята

более общая модель, оценки некоторых параметров

которой

будут

незначимыми.

Другая

возможная ошибка со-

стоит в

том,

что может быть

отвергнута

более общая адекват-

ная

модель и принята модель с ограничениями, что приве-

дет к некорректным значениям параметров. Следовательно,

РИ

анализе статистических критериев нежелательно поль-

за Нельсон показывает, что эта статистика приближенно равна

'«и, которую используют

А.

Зельнер

Ф. Пальм

(115].

189

зоваться очень низкими уровнями значимости, такими, как

0,01 или 0,001. Это

какой-то мере оправдывает обычную

практику принятия решения

пользу более общей модели

сомнительных случаях.

Недостаток рассмотренных статистических критериев

том, что они позволяют сравнивать

две

модели лишь

том

случае, когда одна из них является более общей ло отноше-

нию

другой, т.е.

(р

рц\

ft <

<7г).

не

могут

быть исполь-

зованы

тех

случаях, когда

;

) или {р

>Р*\ <7i<<7a)-

После

того как модель выдержала диагностическую про-

верку

статистические критерии свидетельствуют

ее обо-

снованности,

можно переходить

прогнозированию.

Прогнозирование

Пусть

момент

необходимо сделать прогноз величины

Xt+t,

Т> 1.

Проще

всего осуществлять прогнозирование рекурсивно

непосредственно

по

разностному уравнению x

+t =*

=Ч

1#ш-1+

•••

+ Ур+d

^f+i-p-d

—

Qie*+i-i—-•—

последовательно полагая

i = 1, 2, ..., х

заменяя

Xj для

< t + i

их

прогнозами, полученными

на

предыдущих

шагах.

Доверительные границы прогнозов.

Дисперсия ошибки прогноза на

шагов вперед есть матема-

тическое ожидание

от

е%

(t)

{xt+%

—

х%

(t)}*,

соглас-

но

(7.37)

дается выражением*.

Оценка

с|

может быть получена

уже на

стадии оценки

параметров как средний квадрат ошибок ретроспективного

прогнозирования

на

один шаг вперед. Веса

можно полу-

чить исходя из следующего:

(7.44)

(7.45)

Подставляем

(7.44)

(7.45):

или

(ß)ij) (В)

(В).

190