Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

— оператор сдвига назад, определенный

следую-

щим

образом: Bx

= x

;

— оператор разности назад: 4x

— x

j =

-(1-Я)*,;

— оператор суммирования:

e^ — белый шум с дисперсией

о%>

Остальные обозначения

будут

введены по

ходу

изложе-

ния.

Модель основывается на гипотезе, что изучаемый процесс

является выходом линейного фильтра, на

вход

которого по-

дан процесс белого шума, т. е. что член ряда x

является

взвешенной суммой текущего и предыдущих значений

вход-

ного потока:

где

[А

= const в общем

случае

является параметром, харак-

теризующим процесс, и оператор^ (В) = 1 + %ß +

"г

••>

Если последовательность %, i|>

•••

конечна или беско-

нечна, но сходится, то фильтр называется устойчивым, а

процесс x

будет

стационарным. Тогда ц — среднее значе-

ние,

вокруг которого процесс варьирует. В противном слу-

чае x

— нестационарен и ц не имеет особого смысла, кроме

как

некой точки отсчета уровня процесса.

Рассмотрим некоторые специфические модели, получае-

мые линейной фильтрацией белого шума.

Типы

моделей

Авторегрессионная модель. В этой мо-

дели текущее значение процесса выражается через конеч-

ную линейную совокупность предыдущих значений про-

цесса и возмущения e

. ^ ^

Если обозначить через

отклонение от среднего x

5=1 x

t — tt, то получаем процесс

(7.1)

где

q>i

= const, i - 1, ..., р,

называемый авторегрессионным процессом порядка р, ко-

торый

будем

обозначать АР (р).

Введем

авторегрессионныи

оператор порядка р:

1г

161

тогда

модель может быть записана экономно:

(7.2)

В этой модели р + 2 неизвестных параметра

ц,

,...,

<т|, которые должны быть оценены по имеющимся

данным

об изучаемом процессе.

Если

последовательно выразить x

я*

и т. д.

через e

_2>-".

то получим эквивалентную запись

через бесконечную взвешенную

сумму

реализаций белого

шума:

(7.3)

Однако здесь количество неизвестных параметров моде-

ли

оказывается бесконечным и форма (7.2) явно предпочти-

тельней. Из (7.2) и (7.3)

следует,

что ij> (В) — Ф"

(В). (7.4)

Процессы

могут

быть стационарными и нестационарны-

ми.

Для того чтобы процесс был стационарным,

коэффи-

циенты

Ф должны быть такими, чтобы веса^, i|)

, ... в

(7.3) образовывали сходящийся ряд; Для решения практи-

ческих задач, как правило, достаточно р ^ 2.

Модель скользящего среднего. Дру-

гим типом модели, имеющим практическую ценность, яв-

ляется модель конечного скользящего среднего, в которой

линейно

зависит от

конечного

числа предыдущих

значений

8, т.е.

(7.5)

Это процесс скользящего среднего порядка q или крат-

ко

СС

(q).

Следует

отметить, что в данном

случае

название

«скользящее среднее» вводит в заблуждение, так как веса

h —Qi, —Q

> •••, —Qq не обязательно должны в сумме да-

вать единицу и не обязательно должны быть положитель-

ными.

Если

введем оператор процесса скользящего среднего

порядка

то модель СС (q) может быть записана кратко:

(7.6)

Она

содержит q + 2 неизвестных параметра (л, Qu

Qt>

*..» Q

, е|. Обычно q — 0, 1, 2,

Смешанйая

модель АРСС. Для достижения боль-

шей

гибкости при построении модели

исследуемых

процес-

сов полезно включать в нее и члены скользящего среднего,

авторегрессионные члены. Это приводит к смешанной мо-

дели АРСС (р, q)\

с р + q + 2 неизвестными параметрами.

Модель может быть записана и так:

Особый практический интерес представляет случай р = 1,

Нестационарные

модели. В этих моделях

используются идеи, разработанные в [36], о возможности

трансформировать нестационарные ряды в стационарные

путем

перехода

от исходного ряда к его разностям соответ-

ствующего

порядка d. Тогда преобразованный, стационар-

ный

ряд можно описать одной из рассмотренных выше мо-

делей.

Введем

обобщенный авторегрессионный оператор

¥ (В) = ф (ß)(l — B)

, где

(В) — стационарный опера-

тор, рассмотренный выше. Тогда модель можно записать

таким образом:

(7.7)

(7.8)

На

практике обычно d = 0,1 или, наконец, 2. Модель

(7.7, 7.8) является более общей и называется интегриро-

ванной

моделью авторегрессии —скользящего среднего

(АРИСС)

порядка (р, d

q). Она называется интегрированной

потому, что соотношение обратное (7.8) есть x

— S w

где

5 — оператор суммирования.

Для преобразования исходного ряда в стационарный мо-

гут использоваться и различные

другие

преобразования.

Например,

для экономических и

других

рядов, характери-

163

зующихся приблизительно экспоненциальным ростом, по-

лезно предварительно применять операцию логарифмирова-

ния

(см. § 4 этой главы).

Включение детерминированной по-

линомиальной тенденции роста в мо-

дель АРИСС. Иногда бывает полезна небольшая модифи-

кация

модели АРИСС путем добавления постоянного члена

правую часть. Это новое слагаемое придает модели наи-

более общий вид:

(7.9)

Если постоянный член Q

опущен, то модель может ото-

бражать ряды, имеющие стохастические тренды (случайные

изменения

уровня, темпа роста и

т.п.).

В общем случае, одна-

ко,

может быть желательным включение в модель детерми-

нированной

функции времени / (t). В частности, можно

включить полином порядка d, если положить Q

Ф 0.

Взяв математическое ожидание от обеих частей равенства

(7.9), получаем

Отсюда

следует,

что модель (7.9) эквивалентна модели

(7Л0)

где щ = w

— [i

Поскольку предполагается, что временной ряд генери-

руется моделью из класса стационарных и обратимых, то

необходимо уяснить требования, накладываемые при этом

на

ее параметры.

Стационарность линейного процесса

Единственное условие стационарности состоит в том,

чтобы i|) (В) сходилась при \В | < 1, где В — комплексное

число*.

Для процесса АР(р) в общем

случае

<р

(В) можно рас-

сматривать как полином порядка р относительно В, поэтому

{В) можно представить в виде ф (В) = (1 — G]ß)X

* Необходимо отличать В — комплексную переменную от В—

оператора сдвига назад. Одинаковое обозначение введено для боль-

шей формализации анализа, ибо

всегда

для получения характерис-

тических уравнений (см. дальше)

требуется

замена оператора сдви-

га назад на комплексную переменную.

164

X(l

— 0

B).,.(\ — G

B).

Тогда, если

все

корни полинома

различны,

Так

как для стационарности процесса последовательность

1|) (В) = ф"

(В)

должна быть сходящейся

при | В | ^ 1, то

необходимо иметь

< 1, i — 1, 2, .... р.

Это требование

эквивалентно

тому,

что

корни выражения

ср

(В) =

долж-

ны

лежать

за

пределами единичного круга. Уравнение

(В) = 0

называется характеристическим. Ясно,

что для

процесса АРСС условия стационарности

те же.

На

параметры процесса скользящего среднего из-за

ко-

нечного числа членов вчр

(В) — Q (В) = 1 — QiB — Q

—

—...—QgBv

никакие ограничения для того, чтобы гаранти-

ровать стационарность,

не

накладываются.

Мы

видели,

что

процесс АРСС является стационарным,

если корни

(В)

— 0

лежат вне единичного круга. На прос-

том примере легко убедиться,

что

если корни лежат внутри

единичного круга,

то

модель проявляет нестационарность.

Особое внимание авторов модели привлек случай, когда

корни

лежат

на

единичной окружности.

Так

появилась

не-

стационарная

модель АРИСС.

Обратимость

Линейный

процесс

может быть записан через взвешенную

сумму

прошлых зна-

чений

х и

аддитивный скачок

или

(7Л1)

где

165

В общем

случае

линейный процесс

(7.11)

обратим, если

веса п

}

- таковы, что л (В) сходится при | В | ^ 1.

Получим одно полезное соотношение, применив оператор

1|) (В) к обеим частям (7.11):

Отсюда ч» (В)п (В) = 1, т.е. я (В) = ар-

(В).

(7.12)

Из

(7.12)

можно получать веса я,

зная-ф,

и наоборот.

Рассмотрим модель x

= (1 — Q

ß) е

в которой

Выражая e

через #

получим &

= (1 — Q

B)—

5^-

Отсюда

(7.13)

так

что для этой модели п/ = — Q[.

Из

выражения

(7.13)

видно, что модель СС(1) выражает-

ся

моделью авторегрессии с бесконечным числом членов.

Справедливо и обратное: модель АР (1) эквивалентна моде-

ли СС с бесконечным числом членов. Это говорит о большой

гибкости модели АРСС (/, /).

Теперь выведем условия, которым должны удовлетво-

рять параметры Q

,..., Qg, для того чтобы гарантировать

обратимость процесса

СС(<7).

Запишем модель следующим об-

разом:

Далее используем уже известный прием (считаем, что

корни

полинома Q (В) различны):

Таким

образом, л (В) сходится при | В |< 1, если | #/1 <

< 1 для / = 1, 2, ..., q. Так как корни Q (В) = 0 есть Я/"

то,

следовательно, условие обратимостидля процесса СС(<?)

заключается в том, чтобы корни характеристического

уравнения Q (В) — 0 лежали вне единичного круга. Для

процесса АРСС условия обратимости аналогичны.

166

На

параметры AP-процесса никакие ограничения для

обеспечения обратимости не накладываются, так как

я (В) — ф (В) — 1 — фд5 — ... —

сррВ"

содержит

•

конеч-

ное

число членов.

Автокорреляционная функция

Автокорреляционная функция в этом методе является

основным

инструментом при построении модели. Изучим ее

свойства сначала для АР-процессов:

(7.14)

Умножим

(7,14)

на #*_&.

Берем

математическое ожидание и получаем разностное

уравнение для автоковариаций R:

Отметим, что М & _

) = 0, когда k >

О,

так как

может включать реализации е, имевшие место до

момента t — k, а они некоррелированы с e

. Разделив все

члены на R

убедимся, что автокорреляционная функция

удовлетворяет разностному уравнению того же вида:

(7,15)

Оно

аналогично разностному уравнению, которому

удов-

летворяет сам процесс x

. Таким образом,

(7.15)

можно за-

писать как

(7Л6)

Учитывая, что

<р

(В) = П (1 - G

B), получаем общее

решение уравнения (7.16):

(7.17)

где Gf\ Go-

, .... Gp

— корни характеристического урав-

нения

Ф (В) = 0 и благодаря условию стационарности

Ю||< 1. Если корни G, различны, то возможны два рлу-

чая

1. Корень Gt вещественный. Тогда член А$ в

(7.17)

геометрически

убывает

к нулю с ростом k (затухающая экс-

понента),

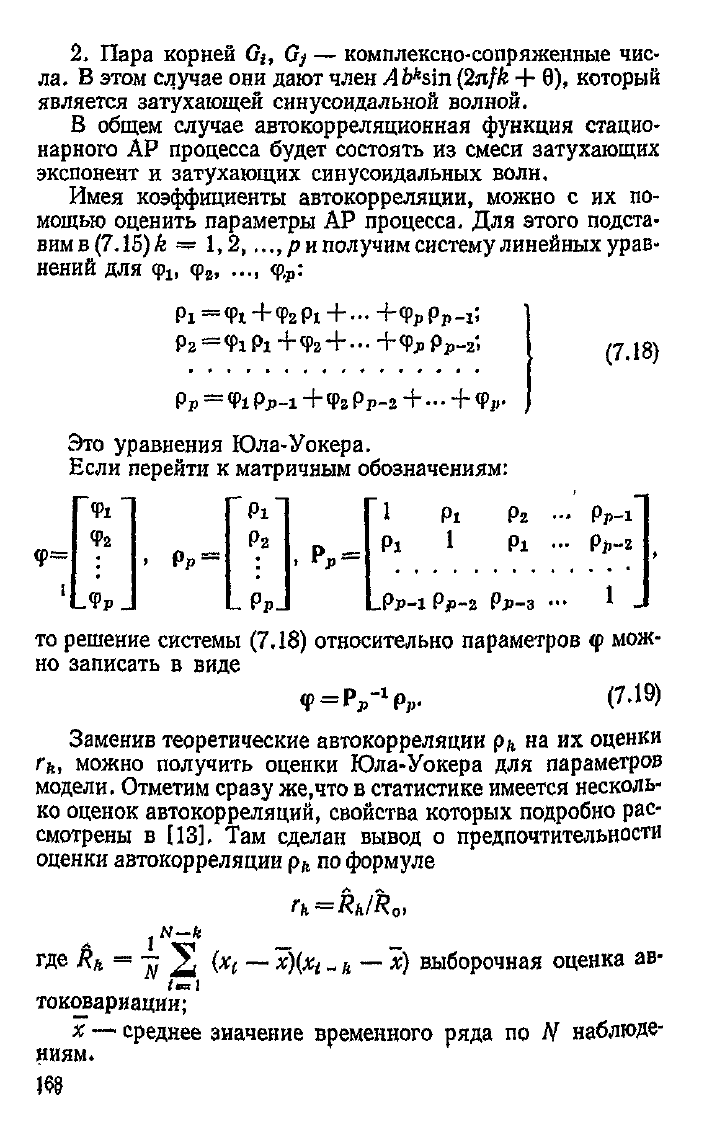
2. Пара корней Gi, Gj — комплексно-сопряженные чис-

ла. В этом

случае

они

дают

член

(2nß + 9), который

является затухающей синусоидальной волной.

В общем

случае

автокорреляционная функция стацио-

нарного АР процесса

будет

состоять из смеси

затухающих

экспонент

затухающих

синусоидальных волн.

Имея

коэффициенты автокорреляции, можно с их по-

мощью оценить параметры АР процесса. Для этого подста-

вим

(7.15)

k —

1,2,...,

получим систему линейных урав-

нений

для фх, ф

, ..., ф

(7.18)

Это уравнения Юла-Уокера.

Если перейти к матричным обозначениям:

то решение системы

(7.18)

относительно параметров

<р

мож-

но

записать в виде

(7Л9)

Заменив

теоретические автокорреляции р& на их оценки

, можно получить оценки Юла-Уокера для параметров

модели. Отметим сразу же,что в статистике имеется несколь-

ко

оценок автокорреляций, свойства которых подробно рас-

смотрены в 113), Там сделан вывод о предпочтительности

оценки

автокорреляции p

по формуле

где выборочная оценка ав-

токовариации;

— среднее значение временного ряда по W наблюде-

ниям.

№

Обратимся теперь к СС-процессам. Получим сначала ав-

токовариационную функцию:

Отсюда дисперсия процесса

будет:

(7.20)

Следовательно, автокорреляционная функция

будет:

(7.21)

Итак,

для к > q автокорреляционная функция СС-про-

Десса равна нулю. Другими словами, автокорреляционная

функция

процесса скользящей средней обрывается при ла-

ге q. Это значит, что по автокорреляционной функции можно

для процессов СС определить численное значение q.

Учитывая, однако, что имеются лишь

грубые

оценки

Гц,..., г„, необходим некий показатель того, насколько оце-

ненное

значение r

может отличаться от соответствующего

теоретического значения, в частности, для суждения, яв-

ляются ли автокорреляции нулями после некоторого лага

q. Для этих лагов можно подсчитать стандартные ошибки

оценок

ПО

упрощенной формуле Бартлетта:

В [22, вып. 2, с.46] показано, как определить стандартные

ошибки

оценок r

в общем случае. „ .

По

оценкам г

, используя q уравнении (7.21),

можно получить оценки Q

, Q

Q„. Однако в отличие от

Уравнений Юла-Уокера для AP-процессов, которые являют-

ся

линейными;

уравнения

(7.21)

являются

нелинейными.

По-

этому, за исключением простого случая, когда q - 1, эти

Уравнения должны решаться итеративно. ,

лппопопипн

Наконец,

для смешанных процессов автокорр^еляцион

ная

функция может быть выведена аналогично

тому,

как она

169

выводилась

для

AP-процесса. Автоковариационная функ-

ция

здесь удовлетворяет разностному уравнению:

(7.22)

где

(k) —

М (x

) —

йзаимная ковариационная

функция

между

я и е

Выражение

(7.22)

означает,

что

Таким

образом, для процесса АРСС (р, q)

будет

авто-

корреляций

, р

1,...,

рх, значения которых зависят и от

параметров скользящего среднего и от автокорреляционных

параметров.

величин

, Рд-!, ...,

Pg-jo

составляют необхо-

димые начальные значения

для

разностного уравнения

(7.23), которое затем полностью определяет автокорреля-

ции

более высокими лагами. Если

q — р < 0, вся

авто-

корреляционная

функция

ру,

/ = 0,

1,2,...

будет

выражать-

ся

совокупностью

затухающих

экспонент и (или)

затухаю-

щих синусоидальных волн,

а ее

свойства

будут

определять-

ся

полиномом

{В)

ир

начальными значениями автокор-

реляционной

функции. Если, однако,

q — р^О, то

будет

q-^-p^rl

значений

, p

..., p

выпадающих

из

данной схемы.

Эти

моменты полезны

при

идентификации

смешанных процессов.

Частная автокорреляционная функция

При

построении модели вначале неизвестно, какого

по-

рядка авторегрессионный процесс надо ставить

соответст-

вие фактическому

ряду.

Инструментом решения этого воп-

роса-служит частная автокорреляционная функция. Здесь

используется тот

факт,

что

процесс

АР

(р), имеющий авто-

корреляционную функцию с бесконечным числом членов,

по

своей природе может быть описан

помощью

ненулевых

функций

от

автокорреляций.

170