Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

ленность системы резко возрастает

—

прошлые данные

те-

перь не

дают

информации

относительно нового уровня,

за-

тем быстро уменьшается

получением новых фактических

данных. Поведение

точке

D, где

имеет место изменение

коэффициента

линейного"

роста, отличается своеобразием.

Фактически истинное событие в течение некоторого времени

скрыто нормальной колеблемостью. Если последовательно

открывать

на

графике данные,

то

вплоть

до

t =

44,45

не

ясно,

было

ли

это изменение

коэффициенте роста, и

даже

после этого момента представление о его величине далеко от

определенности. Байесовская система

целом оказывается

весьма неопределенной относительно значений уровня

коэффициента

линейного роста,

но

она становится более чув-

ствительной, постепенно адаптируется'

возвращается

нормальному состоянию

по

мере того,

как

последующие

данные

подтверждают

новое направление развития ряда.

Исследование чувствительности этой системы показало,

что

ее

эффективность

(с

точки зрения точности прогнозов)

слабо зависит от четырехкратных ошибок в оценкеD

. Столь

большие ошибки

оценке этой величины на практике пред-

ставляются почти невероятными.

Несмотря на то что описанный

метод

не получил распро-

странения

требует

большего объема вычислений, чем ме-

тоды

Хольта,

Брауна или Бокса

Дженкинса (см.

гл. 7),

он

представляет значительный интерес и

заслуживает

изуче-

Таблица 6.3

Варианты значений Относительных дисперсий

в байесовской модели с

четырьмя

состояниями,

использовавшиеся при прогнозировании _____

151

Состояние

Отсутствие

изменений

Ступенчатое изменение

Изменение

скорости роста

Случайное импульсное

от-*

клонение

Вариант

"о

о'

Вариант

№

Вариант

101

100

№

Таблица

6.4

Варианты априорных вероятностей

четырех

состояний

в байесовской модели,

использовавшиеся

при

прогнозировании

Состояние

Отсутствие

изменений

Ступенчатое изменение

Изменение

скорости .роста

Случайное импульсное

от-

клонение

Вероятность

вариант

№

0,425

0,050

0,425

0,100

вариант

№

0,250

0,050

0,600

0,100

вариант

№

0,600

0,050

0,250

0,100

вариант

№

0,800

0,050

0,100

вариант

№6

0,900

0,003

0,094

Таблица

6.5

Варианты значений параметров байесовской модели

с четырьмя состояниями,

из

которых отыскивался наилучший вариант

№

варианта

значений

параметров

№ варианта

значений

от-

носительных

дисперсий

(см.

табл.

6.3)

№ варианта

априорных

вероятно-

стей состоя-

ний

(см.

табл.

6.4)

15»

152

* Вариант

Ni 15

является рекомендацией автороп

метода

в (06].

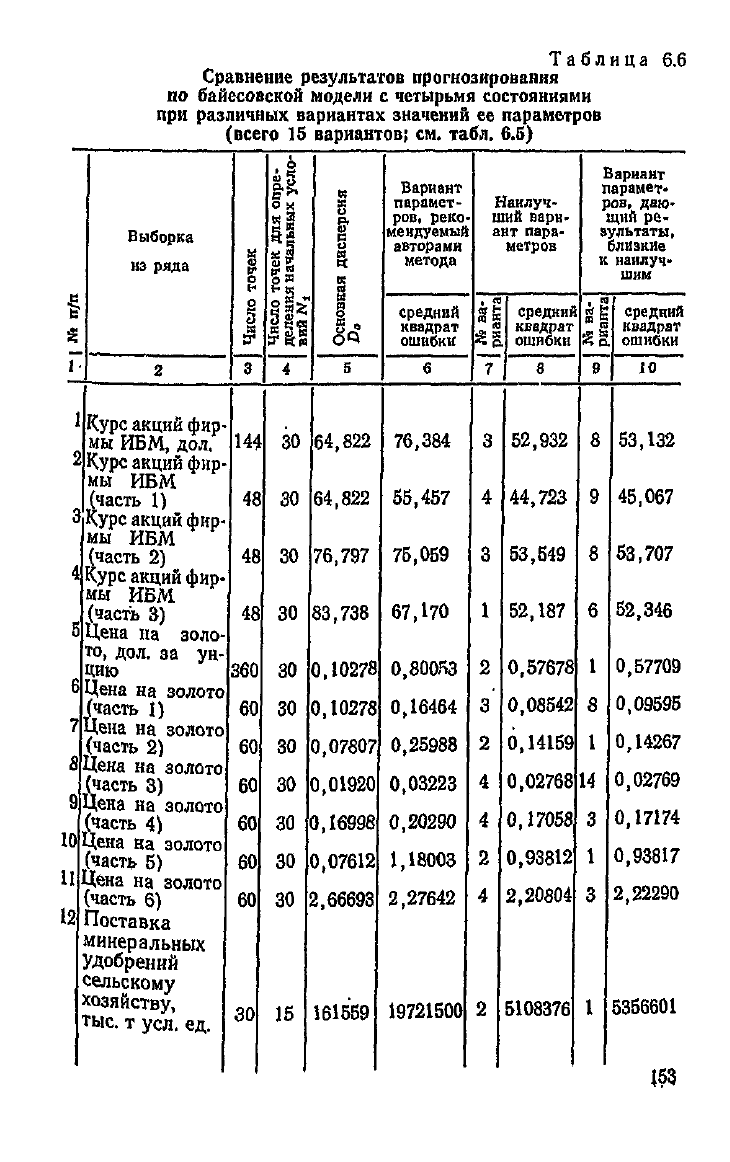
Таблица

6.6

Сравнение

результатов

прогнозирования

по

байесовской модели

четырьмя состояниями

при

различных вариантах значений

ее

параметров

(всего

вариантов;

см.

табл.

6.5)

п/п

Выборка

из

ряда

Курс

акций

фир-

мы

ИБМ,

дол.

Курс

акций

фир-

мы

ИБМ

(часть

Курс

акций

фир-

мы

ИБМ

(часть

Курс акций

фир-

мы

ИБМ

(часть

Цена

на

золо-

то,

дол. за ун-

цию

Цена

на

золото

(часть

Цена

на

золото

(часть

Цена

на

золото

(часть

Цена

на

золото

(часть

Цена

на

золото

(часть

Цена

на

золото

(часть

Поставка

минеральных

Удобрений

сельскому

хозяйству,

тыс.

т усл. ед.

(•>

144

360

е-

:ло-

«а

gii

о»

sis

64,822

76,797

83,738

0,10278

0,07807

0,01920

0,16998

0,07612

2,66693

161659

Вариант

парамет-

ров, реко-

мендуемый

авторами

метода

средний

квадрат

ошибки

76,384

55,457

75,059

67,170

0.800ЯЗ

0,16464

0,25988

0,03223

0,20290

1,18003

2,27642

19721500

Наилуч-

ший

вари-

ант пара-

метров

т pi

™

•Si

«5 а

средни!

квадрат

ошибки

52,932

44,723

53,549

52,187

0,57678

0,08542

6,14159

0,02768

0,17058

0,93812

2,20804

5108376

Вариант

парамет-

ров, даю-

щий

ре-

зультаты,

близкие

• я

наилуч-

шим

средний

квадрат

ошибки

53,132

45,067

53,707

52,346

0,57709

0,09595

0,14267

0,02769

0,17174

0,93817

2,22290

5356601

153

«01

154

Выборка

из

ряда

Производство

электроэнер-

гии,

млрд.

кВт-ч

Производство

гидроэлектро-

энергии,

млрд

кВт-ч

в*

~т

Сумма

вкладов

населения

сберкассы,

млн.

руб

Численность

городского

населения,

млн.

чел.

Протяжен-

ность нефте-

нефтепродук-

топроводов,

тыс.

км

Грузооборот

нефте-

нефтепродук-

топроводов,

гкм

Урожайность

с га

Урожайность

картофеля,

с га

Урожайность

овощей,

с га

1роизводство

яиц,

млрд.

шт.

Ь1

# 2

§£

а;

&•

S-J

«^

"Л.

Igs

«я

№

О.

й)

№

о в

ОС1

158,92

26,280

186324

1,0546

0,53562

382,646

0,63794

38,720

6,142

,51425

Вариант

параметре»

рекомен-

дуемый

авторами

метода

средний

квадрат

ошибки

461,50

48,825

212,8-10

1,1694

6,09359

2052,27

2,54825

70,871

81,834

4,11174

Наилуч-

ший

вари-

ант

пара-

£g

метров

средний

квадрат

ошибки

59,315

30,743

34.307Х

ХЮ5

0,4961

1,50304

529,64

2,49374

170,635

81,231

2,26763

Вариант

парамет-

ров,

даю-

щий

ре-

зультаты,

близкие

наи-

лучшим

средний

квадрат

ошибки

59,995

30,752

38.32Х

xios

0,5008

1,52253

538,76

2,52021

170,825

81,699

2,26091

Продолжение

йия.

Прежде всего желательно сопоставить его эффектив-

ность с точностью прогнозов, получаемых другими метода-

ми.

Между тем практическому использованию описанного

метода посвящена, по-видимому, лишь одна работа [63].

Поэтому нами были проведены эмпирические сопоставле-

ния,

результаты которых приведены в следующем парагра-

фе.

Первые значения параметров распределения

коэффи-

циентов (а

), необходимые для начала рассмотренной в

этой

главе

итеративной процедуры, и основная дисперсия D

определялись нами путем оценивания линейной регрессии

на

первых N

точках выборки. Считалось, что Q</>

Р/>

Рассмотрим соответствующий пример.

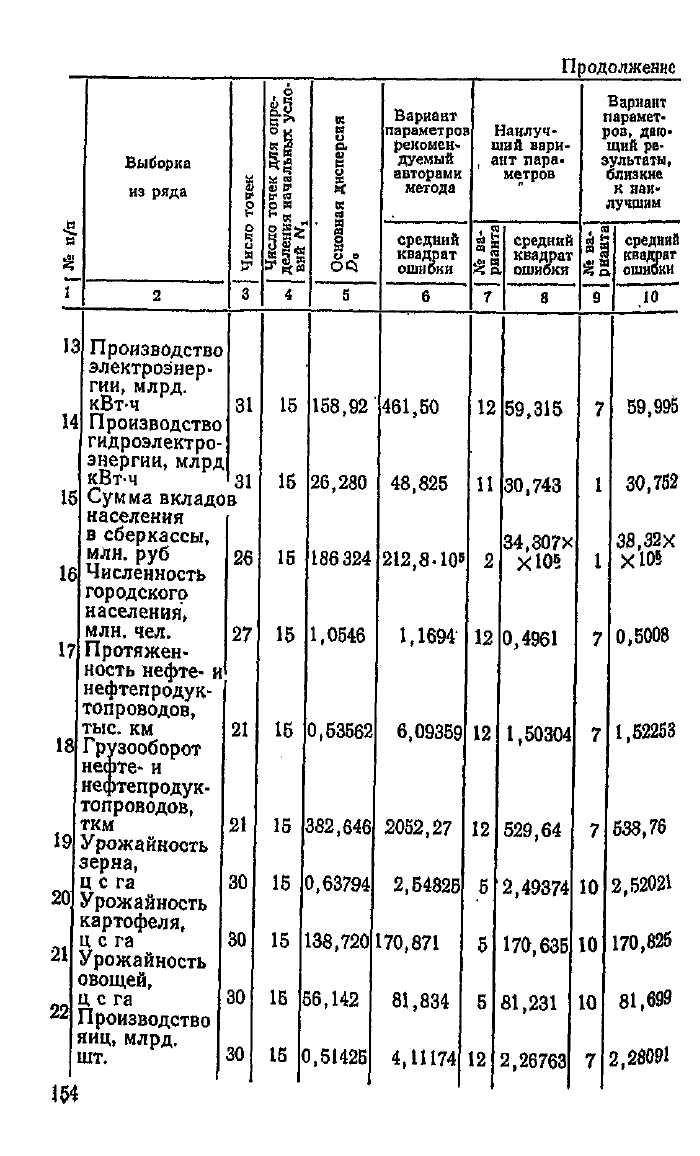
Байесовская

модель с 4 состояниями была испытана на-

ми

на 22 выборках различного объема. Было, опробовано

15 вариантов задаваемых значений параметров модели

(см.

табл. 6.3, 6.4, 6.5), из которых вариант № 15 представ-

лял значения, рекомендуемые авторами метода.

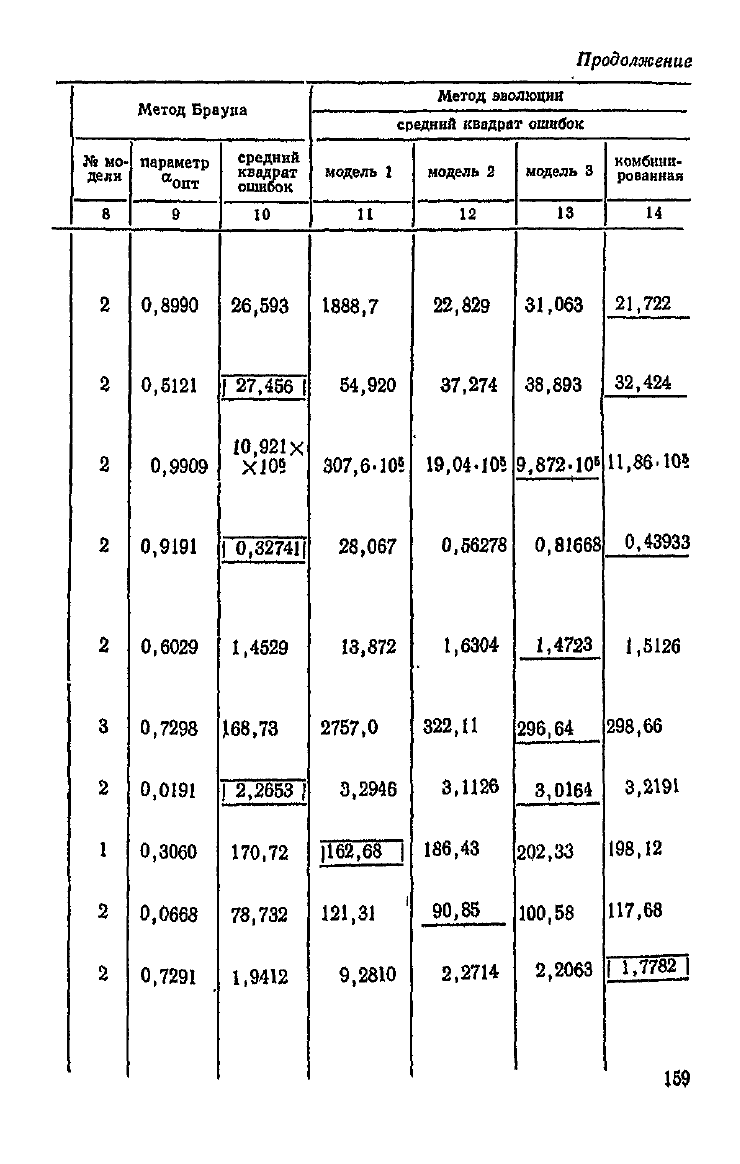
"Результаты, приведенные в табл. 6.6,

свидетельствуют

том, что рекомендация авторов относительно значений па-

раметров не получила экспериментального подтверждения.

Анализ результатов приводит к

выводу,

что средний квад-

рат ошибки особенно чувствителен к значениям априорных

вероятностей состояния процесса.

§ 4. СРАВНЕНИЕ МЕТОДОВ

Теперь, познакомившись с разнообразными моде-

лями

адаптивного типа, целесообразно провести эмпиричес-

кое сравнение точности получаемых по ним прогнозов.

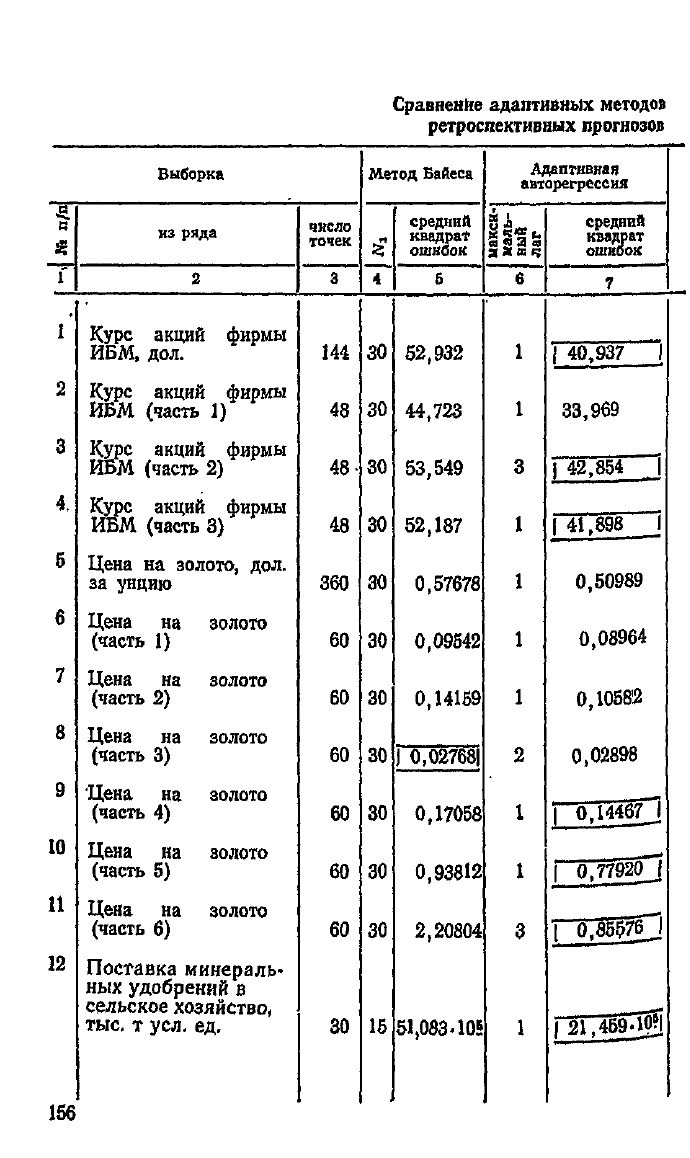
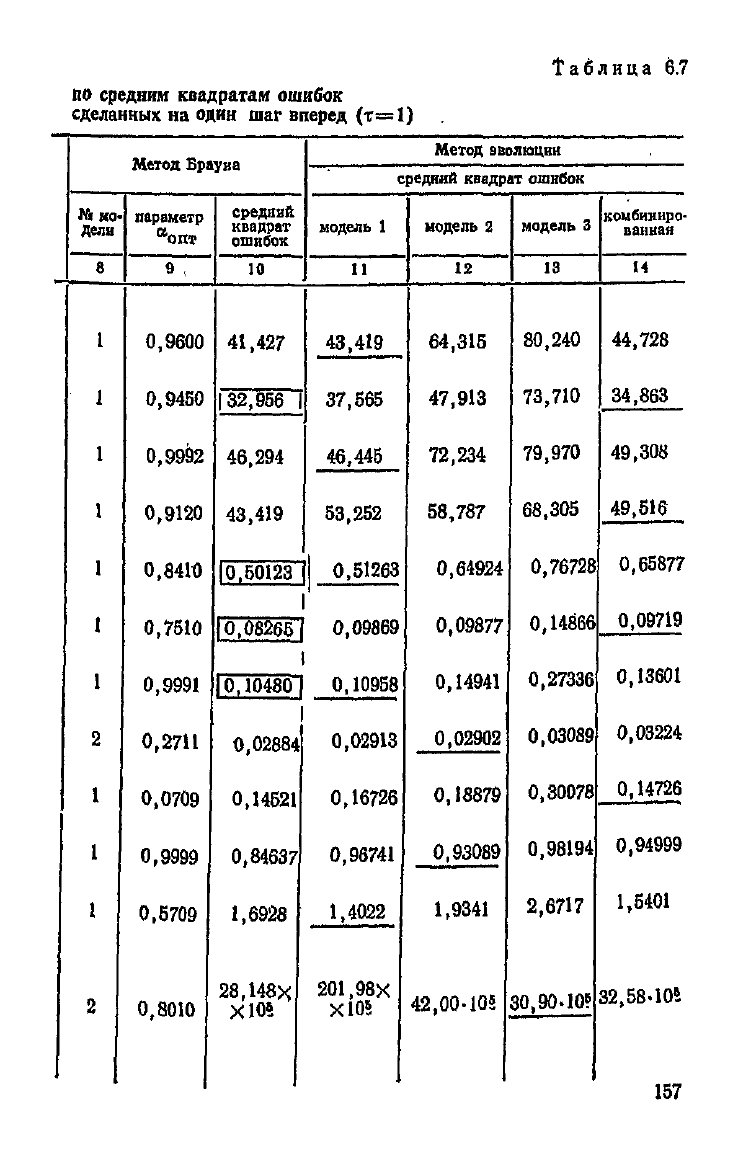
Результаты испытаний адаптивных моделей представле-

ны

в сводной табл. 6.7. В ней прямоугольником выделен

результат,

наилучший в строке, а подчеркнут —

результат,

лучший из тех, которые

дают

модели метода эволюции един-

ственного параметра адаптации. Номера моделей в графах

11,12,13

означают: №

— полиномиальная модель нуле-

вого порядка, № 2 — полиномиальная модель первого по-

Рядка,

№ 3 — полиномиальная модель второго порядка.

Как

видно из таблицы, превосходство осталось за адап-

тивной

моделью авторегрессии, рассмотренной в гл. 3. Со-

вершенно не выдерживает конкуренции намного более слож-

ная

байесовская модель с 4 состояниями

(см.

выборки №11,

*2,13,15,18).

Остальные модели в общем ненамного отстают

от модели адаптивной авторегрессии.

155

Сравнение

адаптивных методов

ретроспективных прогнозов

166

Курс

ИБМ,

Курс

ИБМ

Курс

ИБМ

Курс

ИБМ

Выборка

из

ряда

акций

фирмы

дол.

акций

фирмы

(часть 1)

акций

фирмы

[часть 2)

акций

фирмы

(часть 3)

Цена

на золото, дол.

за унцию

Цена

(часть

Цена

(часть

Цена

(часть

Цена

(часть

Цена

(часть

Цена

(часть

на

золото

на

золото

на

золото

на

золото

на

золото

на

золото

Поставка

минераль-

ных удобрений в

сельское хозяйство,

тыс.

т усл. ед.

число

точек

144

48-

360

Метод

Байеса

1Б

средний

квадрат

ошибок

52,932

44,723

53,549

52,187

0,57678

0,09542

0,14159

| 0,02768|

0,17058

0,93812

2,20804

51,083405

Адаптивная

авторегрессия

a S 3

<и

зав«:

средний

квадрат

ошибок

40,937

33,969

42,854 . !

41,898

0,50989

0,08964

0,10582

0,02898

0.14467J

O.7792ÜJ

'[" 0,8557]П

21,459

ЛОЯ

ta6fl«ua

6.7

по

средним

квадратам

ошибок

сделанных

на

один

шаг

вперед

(т—1)

Метод

Брауна

№

мо-

дели

параметр

опт

о,

,9600

,9450

,9992

,9120

,8410

,7510

9991

2711

0709

9999

6709

8010

средний

квадрат

ошибок

41,427

132,956 I

46,294

43,419

10.50123

10,08265

10,10480

0,02884

0,14521

0,84637

1,6928

28.148Х

ХЮ5

Метод

эволюции

средний

квадрат

ошибок

модель

1.°

о,

,419

,565

,445

,252

,51263

09869

10958

02913

16726

96741

4022

201.98Х

Х108

модель

о,

,315

,913

,234

,787

,64924

09877

14941

02902

18879

93089

9341

42,00-105

модель

80,240

73,710

79,970

68,305

0,76728

0,14866

0,27336

0,03089

0,30078

0,98194

2,6717

30,90.10?

комбиниро-

ванная

44,728

34,863

49,308

49,516

0,65877

0,09719

0,13601

0,03224

0,14726

0,94999

1,5401

32,58-105

157

158

Выборка

из

ряда

2 '

Производство электрс

энергии,

млрд.

кВт-ч

Производство гидро-

электроэнергии,

млрд.

кВт-ч

Сумма

вкладов насе-

ления

в сберкассы,

млн.руо

Численность

город-

ского населения,

млн,

чел.

Протяженность

нефте-

и нефтепро-

дуктопроводов,

тыс. км

Грузооборот

нефте-

нефтепродуктопро-

водов, ткм

Урожайность зерна,

с га

Урожайность карто-

феля,

ц с га

Урожайность овощей,

с га

Производство яиц,

млрд. шт.

число

точек

Метод

Байеса

средний

квадрат

ошибок

59,315

30,743

34.307Х

Х105

0,4961

1,50304

529,64

2,4937

170,63

81,231

2,2676

Адаптивная

авторегрессия

макси-

маль-

ный

лар

средний

квадрат

ошибок

19,115

34,933

18,45810-10?

0,37938

1,1703

99,479__

3,1536

165,24

71,758

2,0802

Продолжение

159

Метод Брауна

№ мо-

дели

параметр

опт

0,8990

0,5121

0,9909

0,9191

0,6029

0,7298

0,0191

0,3060

0,0668

0,7291

средний

квадрат

ошибок

26,593

27,456 |

W.921X

ХЮ5

0.3274Ц

1,4529

Л68.73

2,2653 |

170,72

78,732

1,9412

Метод эволюция

средние

квадрат

онгабок

модель

1888,7

54,920

307,6.105

28,067

13,872

2757,0

3,2946

1162,68 |

121,31 '

9,2810

модель

22,829

37,274

19,04-105

0,56278

1,6304

322,11

3,1126

186,43

90,85

2,2714

модель

31,063

38,893

9,872.10*

0,81668

1,4723

296,64

3,0164

202,33

100,58

2,2063

комбини-

рованная

21,722

32,424

11,86.105

0,43933

1,5126

298,66

3,2191

198,12

117,68

1,7782

Глава 7

МОДЕЛИ

АВТОРЕГРЕССИИ —

СКОЛЬЗЯЩЕГО

СРЕДНЕГО

(МЕТОД

БОКСА —ДЖЕНКИНСА)

главе

излагается метод построения смешанных

моделей авторегрессии — скользящего среднего,

исследуют-

ся

свойства моделей, проводится их эмпирическое сравне-

ние

с адаптивной моделью авторегрессии, рассмотренной

гл. 3. Здесь рассматриваются модели для временных ря-

дов без эффекта сезонности.

§ 1. ОБЩЕЕ ОПИСАНИЕ МОДЕЛЕЙ И ИХ СВОЙСТВ

Еще одно направление развития и обоснования

адаптивных моделей дано в работе Дж. Бокса и Г. Джен-

кинса

15]. В их книге особое внимание

уделено

проблеме

выбора модели и ее

оцениванию,

что и вызвало интерес

спе-

циалистов. Однако недостаточное количество практичес-

ких примеров прогнозирования с использованием этого ме-

тода

вызывает определенные

сомнения.

Возникает необходи-

мость проверить метод наделе, сравнить его

другими

мето-

дами.

Прежде всего кратко опишем модели, лежащие в осно-

ве процедуры прогнозирования, и методы построения этих

моделей, а затем проанализируем особенности их приме-

нения

и конкретные результаты, полученные при проведе-

нии

экспериментов.

Для описания моделей потребуются следующие опера-

торы

и обозначения:

— значение ряда в момент /;

правомерности

особенностях алгебраических действий

над рассматриваемыми операторами см.

(1, приложение А].

100