Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

Глава

АДАПТИВНЫЕ

КОМБИНИРОВАННЫЕ

МОДЕЛИ

В главе предпринята попытка

построения-

более

гибких комбинированных моделей, в состав (базовый на-

бор),

которых

входит

несколько более простых адаптивных

моделей. В комбинированных моделях селективного типа

на

каждом шаге организован автоматический выбор по за-

данному критерию наилучшей модели из числа входящих

базовый набор. Таким образом, адаптация происходит

на

двух

уровнях: по

структуре

или типу модели и по пара-

метрам. В комбинированной гибридной модели прогноз

формируется как взвешенная сумма прогнозов, получен-

ных

по

альтернативным моделям. Веса при этом имеют адап-

тивный характер.

§ 1.

АДАПТИВНАЯ

СЕЛЕКТИВНАЯ

МОДЕЛЬ

Вполне естественно предположить, что реальный

процесс время от времени претерпевает коренные

изменения.

Изменяются

уровень и динамические свойства ряда. При-

чем на одних участках сохраняется прблизительно постоян-

ный

уровень, на

других

ряд растет с определенной ско-

ростью или характеризуется появлением ускорения. Поэ-

тому всякая, попытка подобрать какую-либо одну прогноз-

ную модель для всего ряда приводит к некоей усредненной

модели с чрезмерными дисперсиями оцениваемых парамет-

ров и ошибками прогнозирования. Когда изменение струк-

туры

происходит резким скачком, исследователю довольно

просто отсечь устаревшие данные и строить модель только

на

свежей информации. Однако гораздо чаще изменения

коренных свойств ряда происходят не сразу, а непрерывно.

Причем

ряд меняет тенденцию,

делает

зигзаги и бывает

РУДно, а при одновременном исследовании многих рядов

121

даже

невозможно быстро анализировать

такую

динамику

заменять одну модель

другой.

Мы

предлагаем две процедуры адаптации

структуры

модели, которые

могут

выполняться на ЭВМ. Одна из них

основывается на принципе непрерывной селекции.

Предположим,

что • рассматриваемый процесс генери-

руется моделью с постоянным уровнем, моделью с линей-

ным

ростом, квадратической моделью поочередно. Учиты-

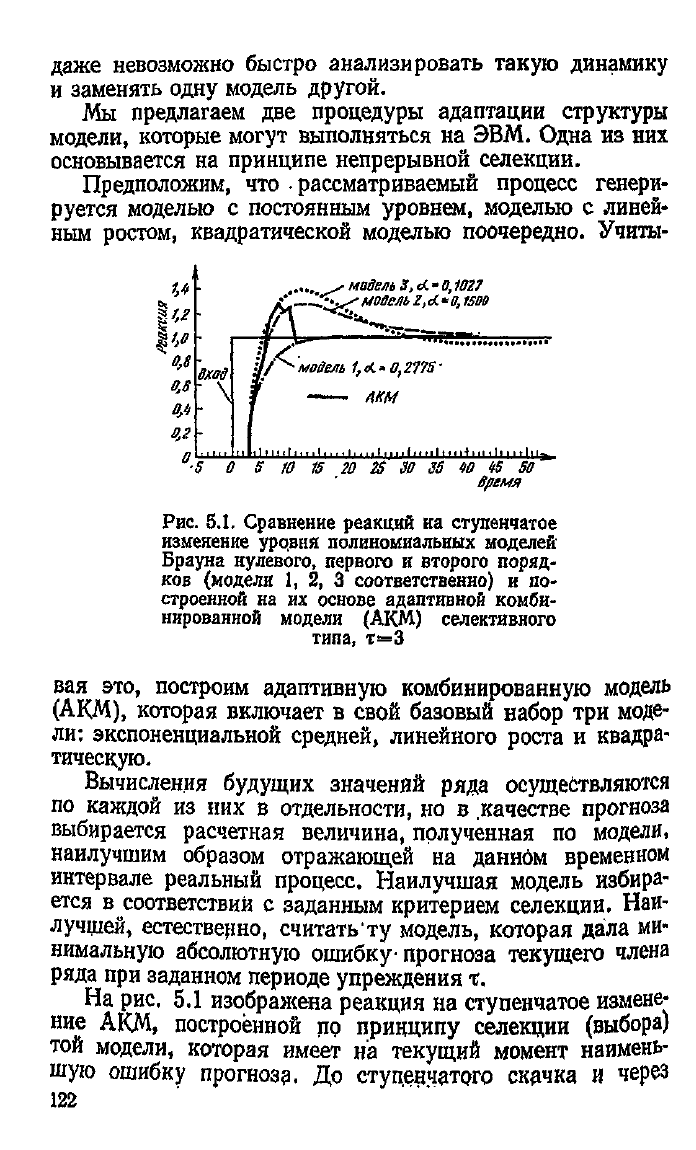
Рис.

5.1. Сравнение реакций на ступенчатое

изменение

уровня полиномиальных моделей

Брауна нулевого, первого и второго поряд-

ков

(модели 1, 2, 3 соответственно) и по-

строенной

на их основе адаптивной комби-

нированной

модели (АКМ) селективного

типа, т=3

вая

это, построим адаптивную комбинированную модель

(АКМ),

которая включает в свой базовый набор три моде-

ли:

экспоненциальной средней, линейного роста и квадра-

тическую.

Вычисления

будущих

значений ряда осуществляются

по

каждой из них в отдельности, но в .качестве прогноза

выбирается расчетная величина, полученная по модели,

наилучшим образом отражающей на данном временном

интервале реальный процесс. Наилучшая модель избира-

ется в соответствий с заданным критерием селекции. Наи-

лучшей, естественно, считать "ту модель, которая

дала

ми-

нимальную абсолютную ошибку- прогноза текущего члена

ряда при заданном периоде упреждения t.

На

рис. 5.1 изображена реакция на ступенчатое измене-

ние

АКМ, построенной цр принципу селекции (выбора)

той модели, которая имеет на текущий момент наимень-

шую ошибку прогноза. До ступенчатого скачка и через

122

— 1 единиц времени после его появления все три модели,

входящие в базовый набор предикторов,

дают

одинаковые

т-прогнозы. Это приводит к затруднению при выборе про-

гнозирующей модели. В такой ситуации для большей опре-

деленности можно взять модель линейного роста в качестве

компромисса

между

моделью скользящей средней и квад-

ратической моделью. В момент t = 3 становится ясно, что

квадратическая модель

дает

результаты, более близкие

реальным точкам. АКМ переключается на нее. В даль-

нейшем из-за заметного превышения этой моделью уровня

ступенчатого скачка АКМ переключается на модель линей-

ного роста и модель экспоненциальной средней, но пере-

ключение это происходит не сразу, а с лагом т = 3. Такая

задержка

ухудшает

общий

результат.

Ясно, что наиболее

эффективно

в данном

случае

критерий селекции должен

работать при малых т.

В рассмотренном примере АКМ испытывалась на

вход-

ном

потоке данных, содержащем детерминированный сту-

пенчатый скачок. Если тот же эксперимент провести в более

жизненных условиях, при наличии помех, то столь простой

критерий селекции

будет

не

всегда

удовлетворителен, так

как

из-за случайной составляющей лучший

результат

будет

то у одной, то у

другой

модели. Таким образом, нельзя

общем

случае

исходить только из последней ошибки про-

гнозирования.

Необходимо учитывать некоторую их со-

вокупность. Имеется довольно много вариантов построения

критерия

селекции. Предложим, например, два таких

критерия.

Критерий

К' Переключение на данную модель

осуществлять

тогда,

когда К ее последних прогнозов яв-

ляются наилучшими в сравнении с прогнозами по

другим

моделям, входящим в базовый набор АКМ.

Критерий

В. Переключение на данную модель

осуществлять

тогда,

когда ее экспоненциально сглаженный"

квадрат ошибки прогнозирования В минимален по сравне-

нию-с аналогичным показателем для остальных моделей

базовом наборе АКМ.

Критерий

В формируется следующим образом:

где 0 < а в < 1 — параметр сглаживания;.

е%

у __

) _ ошибка прогноза, сделанного в мо-

мент / - т на t шагов вперед.

123

Легко заметить, что при а

= 1 критерий В эквивален-

тен критерию К при К — 1.

Если раньше отмечалось, что, в модели экспоненциаль-

ного типа параметр сглаживания часто бывает близок

0, то здесь этого сказать нельзя. Параметр В характери-

зует

инерционность переключения, а мы уже видели, что

промедление с переключением может привести к плохой

работе АКМ, нарушить, соответствие

структуры

модели

динамике процесса. То же относится к критерию /С.

По

существу,

величину B

можно было бы назвать оцен-

кой

текущего значения дисперсии ошибки прогноза на х

единиц времени вперед. Но учитывая, что а

обычно ве-

лико,

сглаживание квадратов ошибок

будет

недостаточным.

Поэтому придавать величине В такой смысл в общем

случае

было бы неоправданным. При малых значениях параметра

сглаживания эта интерпретация допустима и аналогичная

процедура может использоваться для

грубой

оценки дове-

рительных уровней прогнозов при прогнозировании не-

стационарных процессов.

Принцип

непрерывной селекции весьма прост. Но в свя-

зи

с тем, что

переход

с модели на модель зависит от предик-

торов, входящих в базовый набор АКМ, и специфических

динамических свойств ряда, общий теоретический анализ

эффективности

АКМ затруднителен, и мы оставляем решаю-

щее слово за экспериментом (см. § 3).

2. АДАПТИВНАЯ ГИБРИДНАЯ

МОДЕЛЬ

Адаптивная селективная модель рассчитана на

выбор одного предиктора из некоторого их множества.

Но

очевидно, что такой выбор однозначно и эффективно

можно осуществлять, только если модели, входящие в ба-

зовый набор, существенно

различны.

Для тех случаев, когда

АКМ

входят

модели, дающие сравнительно близкие ре-

зультаты,

и селекция затруднена, можно предложить гиб-

ридную АКМ, прогноз по которой является взвешенной

суммой прогнозов, полученных по входящим в нее предик-

торам.

Веса

прогнозов ©

предлагаем взять адаптивными,

обратно пропорциональными величине B

it u

подсчитывае-

мой,

как и в селективной АКМ:

124

Коэффициент

пропорциональности g

определяется из ра-

венства суммы весов единице. Например, для базового

набора из

трех

моделей веса

будут

определяться так:

Получаемый в данном

случае

прогноз

будет

ближе к ре-

зультату,

получаемому то по одной, то по

другой

модели,

являясь

некоторой адаптивной равнодействующей.

В отличие от модели, рассмотренной ранее, гибридная

модель осуществляет переключение более плавно, со мно-

жеством промежуточных положений. В

результате

^полу-

чается непрерывный спектр возможных конструкций про-

гноза.

Для обеих процедур построения АКМ были составлены

программы, которые содержат наборы по 5 моделей: экс-

поненциальной

средней, линейного и квадратического роста

(Брауна или Тригга—Лича) и две «наивные» модели:

Базовый

набор АКМ формируется исследователем или

автоматически из любого сочетания предикторов этого

программного набора.

Автоматическое формирование основано на непрерыв-

ном

сравнении средних квадратов ошибок прогнозов, полу-

ченных по различным моделям к текущему моменту вре-

мени.

Плохие модели

могут

случайно приближаться к ре-

альному процессу и кратковременно давать хорошие про-

гнозы,

что приводит к переключению АКМ именно на них.

результате

появляются большие ошибки, что

ухудшает

эффективность

АКМ. Такие модели

лучше

сразу вывести

из

базового набора. Поэтому если базовый набор формиру-

ется автоматически, то из программного набора моделей

него включаются только те модели, средние квадраты

ошибок

которых не больше чем в т раз превосходят

мини-

мальную из них:

125

Обычно т =

1,2—1,5.

Причем меньшее значение т со-

ответствует

малым t, так как при увеличении периода уп-

реждения разброс средних квадратов ошибок различных

моделей, как правило, возрастает.

При

автоматическом формировании базовый набор не

яв-

ляется раз навсегда определенным. Если

течением времени

меняется соотношение

между

средними квадратами оши-

бок, то меняется соответственно и базовый набор.

Таким образом, при прогнозировании модель подвер-

гается

двум

испытаниям. Одно, основанное на анализе

средних квадратов прошлых ошибок,

дает

ответ на вопрос

о целесообразности включения модели в базовый набор

предикторов. Другое, путем сравнения текущих свойств

моделей по критерию В, определяет ту модель из базового

набора, от которой можно ожидать наилучшего прогноза.

Принципы,

изложенные в этом параграфе, являются до-

статочно общими и

могут

быть применены для построения

АКМ с разнообразными базовыми наборами, в том числе

включающими одинаковые по структуре, но отличающиеся

значениями параметров

модели.

Число предикторов в наборе

не целесообразно брать большим. Обычно достаточно 3—4

модели.

3. ПРИМЕРЫ

Пример 5.1

Построим селективную АКМ. Включим в ее ба-

зовый набор предикторов полиномиальные модели Брауна

нулевого, первого и второго порядков — модели много-

кратного сглаживания с постоянной а = 0,1. Испытаем

эту модель на данных о

Kypcev

акций

фирмы ИБМ и цене

на

золото. На рис. 5.2 представлены прогнозы курса

акций

на т = 3 по АКМ и по каждой из моделей, входящих

в ее базовый набор.

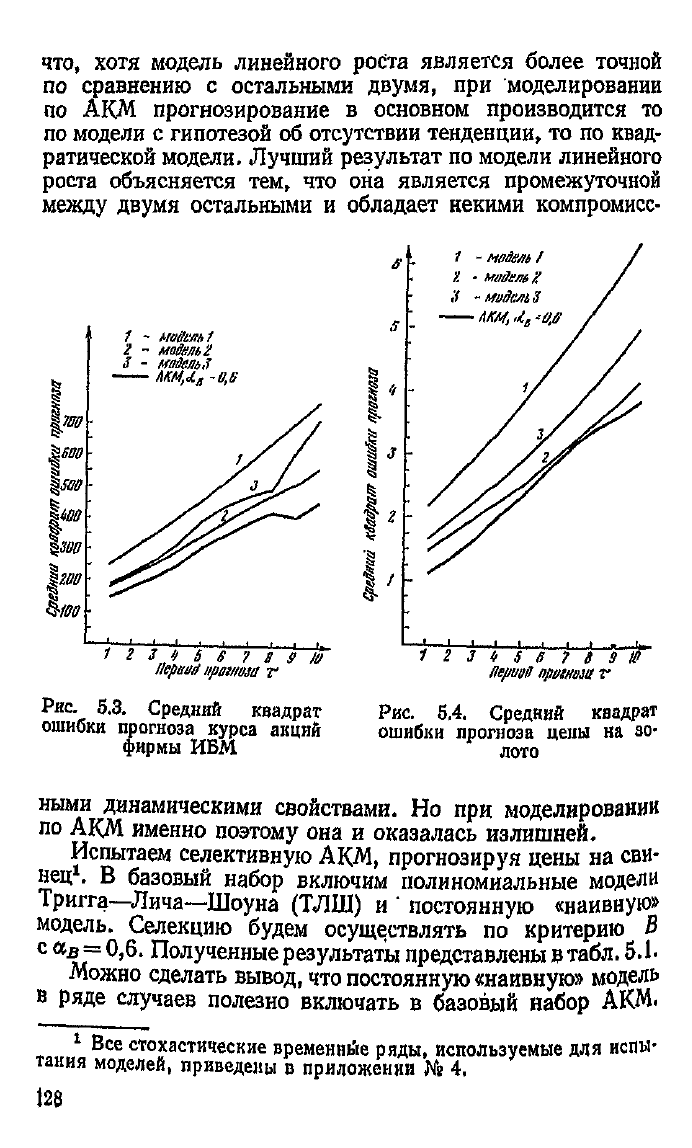
Об эффективности процедуры селекции по критерию В

можно судить по среднему квадрату ошибок прогнозирова-

ния

зависимости отт

(рис,

5.3,5.4).

Как

видим,

применение

процедуры селекции для малых т оказывается полезным и

приводит к уменьшению среднего квадрата

ошибок

прогноза.

Из

графиков также видно, что выбор моделей для ба-

зового набора довольно трудное дело. Казалось бы, что

чем

лучше

работает модель отдельно, тем полезнее

будет

ее

ßKJiK/Wtf

<?->?жй

набор. Но из рис. 5.2

следует,

126

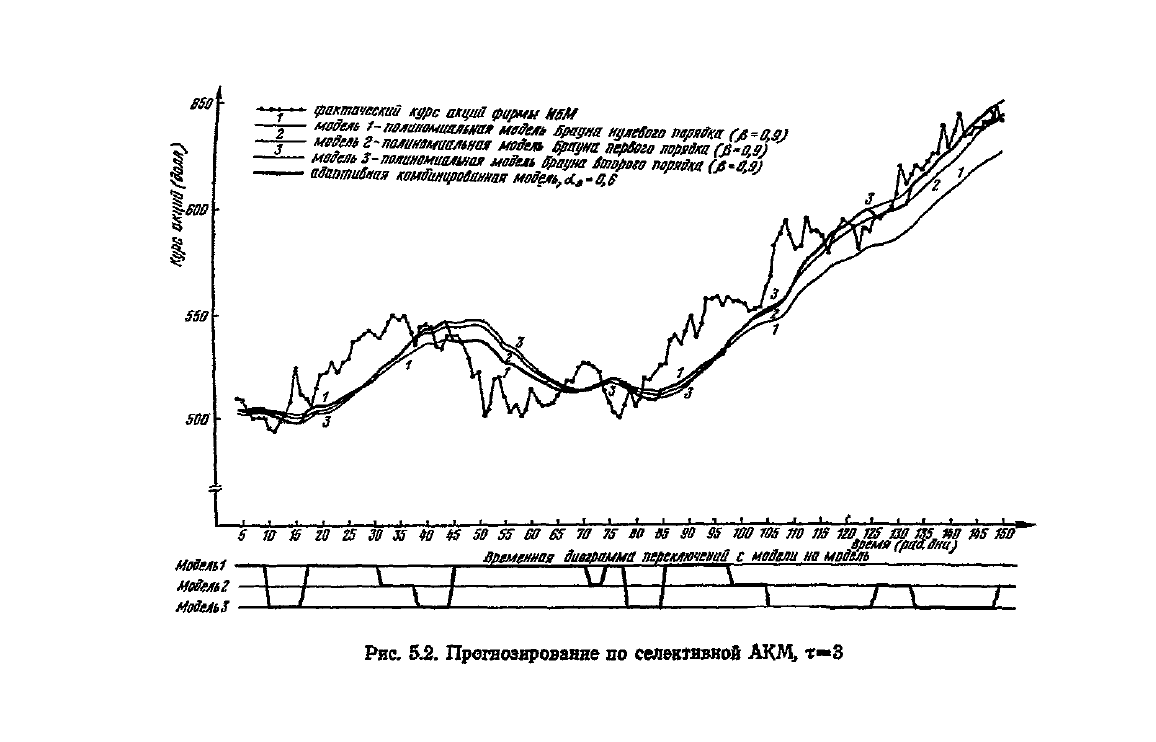
Рис.

5.2. Прогнозирование по селективной АКМ, т—3

что,

хотя

модель линейного роста является более точной

по

сравнению с остальными двумя, при моделировании

по

АКМ прогнозирование в основном производится то

по

модели с гипотезой об отсутствии тенденции, то по квад-

ратической модели. Лучший

результат

по модели линейного

роста объясняется тем, что она является промежуточной

между

двумя

остальными и

обладает

некими компромисс-

Рис.

5.3. Средний квадрат

ошибки

прогноза курса акций

фирмы ИБМ

Рис.

5.4. Средний квадрат

ошибки

прогноза целы на зо-

лото

ными

динамическими свойствами. Но при моделировании

по

АКМ именно поэтому она и оказалась излишней.

Испытаем селективную АКМ, прогнозируя цены на сви-

нец

. В базовый набор включим полиномиальные модели

Тригга—Лича—Шоуна (ТЛШ) и

постоянную

«наивную»

модель. Селекцию

будем

осуществлять по критерию В

° °ЧГ °'

' Полученные

результаты

представлены в табл. 5.1.

Можно сделать вывод, что постоянную

«наивную»

модель

ряде

случаев

полезно включать в базовый набор АКМ.

* Все стохастические временные ряды, используемые для испы-

тания

моделей, приведены в приложении № 4.

128

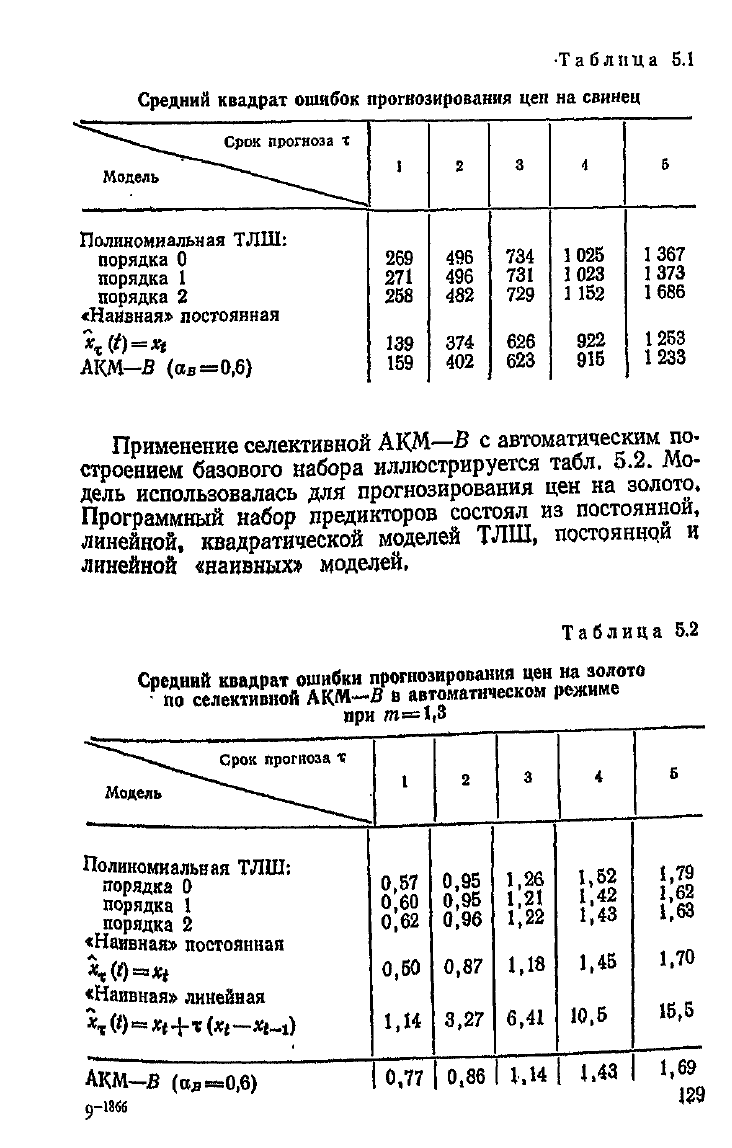
•Таблица 5.1

Средний квадрат ошибок прогнозирования цен на свинец

^^_^^

Срок прогноза

Модель

"""*---^^^

Полиномиальная

ТЛШ:

порядка

«Наивная» постоянная

АКМ—В

(а

=0,6)

269

271

258

139

159

496

482

374

402

734

731

729

626

623

1025

1023

1152

922

915

1367

1373

1686

1253

1233

Применение

селективной АКМ—В с автоматическим по.

строением базового набора иллюстрируется табл. 5.2. Мо-

дель

использовалась для прогнозирования цен на золото.

Программный набор предикторов состоял из постоянной,

линейной,

квадратической моделей ТЛШ, постоянной и

линейной

«наивных»

моделей,

"""•

Срок прогноза

Модель

^**"""**«^^

Полиномиальная

ТЛШ:

порядка

«Наивная» постоянная

«Наивная» линейная

ARM-B

(«в=0,6)

еэскэ |

о,

|о

,77

§:

|о

,86

,14

1 1

,52

,42

,43

,45

,43

1,79

1,62

1,63

1,70

4 Г*

15,5

1,ОУ

JOO

Таблица 5.2

Средний квадрат ошибки прогнозирования цен наi золото

по

селективной АКМ-Я в автоматическом режиме

при

т=1»3

129

9-1866

Как

видим, модель неплохо справилась с выбором по-

лезных предикторов и прогнозов. Можно отметить, что при

т = 1 «наивная» линейная модель явно портит общий ре-

зультат

АКМ. В таких

случаях

рекомендуются два пути.

Во-первых, заведомо

плохую

модель

можно

сразу устранить

перейти на режим принудительного задания базового на-

бора предикторов.

Во-вторых,

при т

1 можно уменьшить

до 1,2. Это позволит осуществлять более строгий отбор

предикторов в автоматическом режиме.

Пример

5.2

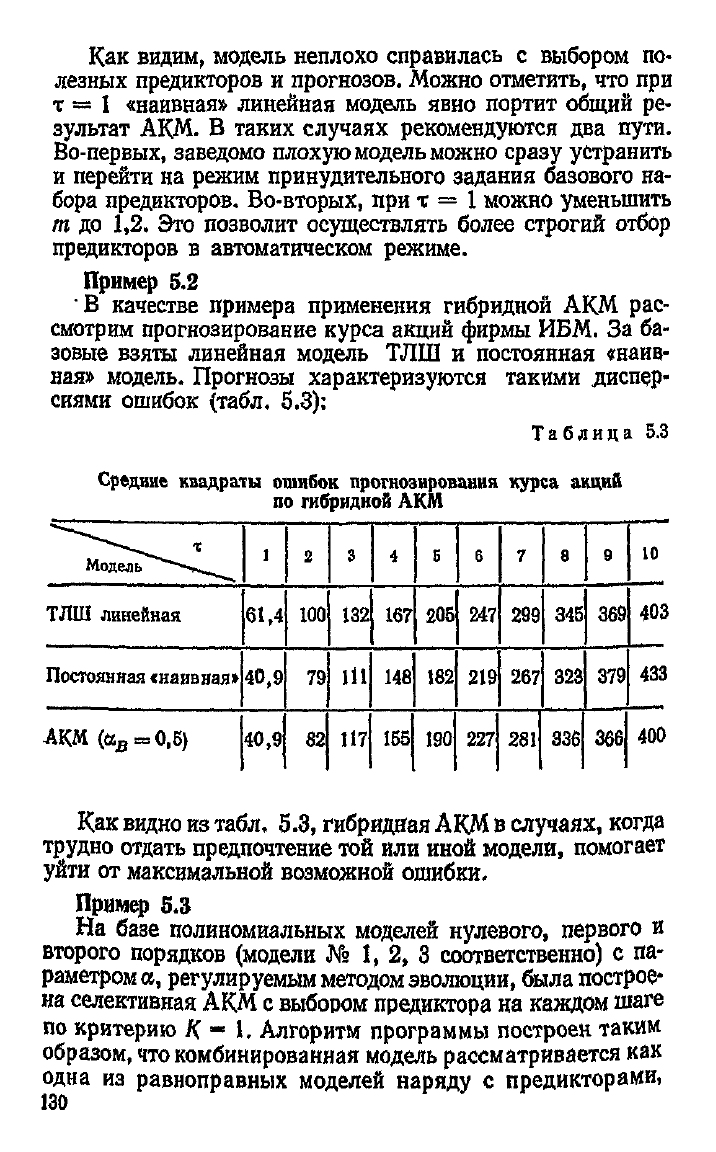
В качестве примера применения гибридной АКМ рас-

смотрим прогнозирование курса акций фирмы

ИБМ.

За ба-

зовые взяты линейная модель ТЛШ и постоянная «наив-

ная» модель. Прогнозы характеризуются такими диспер-

сиями

ошибок (табл. 5.3):

Таблица

5.3

Модель

^*~^~^.^

ТЛШ

линейная

Постоянная

«наивная»

АКМ (03 = 0,5)

61,4

40,9

100

132

117

167

148

155

205

182

190

247

219

227

299

267

281

345

323

336

369

379

366

403

433

400

Как

видно

из

табл. 5.3, гибридная

АКМ

случаях,

когда

трудно

отдать

предпочтение той или иной модели, помогает

уйти от максимальной возможной ошибки.

Пример

5.3

На

базе полиномиальных моделей нулевого, первого и

второго порядков (модели № 1, 2, 3 соответственно) с па-

раметром

а, регулируемым

методом

эволюции,

была построе-

на

селективная АКМ с выбором предиктора на каждом шаге

по

критерию К ** 1.

Алгоритм

программы построен таким

образом,

что

комбинированная

модель рассматривается как

одна из равноправных моделей наряду с предикторами,

130

Средние квадраты ошибок прогнозирования курса акций

по

гибридной АКМ