Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

нию

к текущему наблюдению x

) распределение. В ряде

случаев

будем

отмечать это записью (а

х>t

, а

{!#*)•

Перейдем к проблеме вычисления 'апостериорных ве-

роятностей. Рассмотрим сначала простейший случай, когда

генерирующий процесс (6.1) имеет лишь одно состояние,

т. е. дисперсии D

, D

неизменны во времени. В этом

случае

если совместное распределение (%,

*~1,

, *-i)

момент t — 1 является двумерным нормальным:

где

то апостериорное распределение в момент t также является

двумерным нормальным:

где компоненты вектора Ф

определяются следующим обра-

зом (см. приложение № 2).

Пусть

(6.4)

(6.5)

Далее, пусть

(6.7)

Тогда параметры совместного апостериорного распре-

деления (а

„ а

г t

) в момент t можно вычислить по форму-

лам:

(6.8)

141

Введем

для

всего алгоритма пересчета моментов, задан-

ного выражениями (6.4)—(6.8), обозначение:

(6.9)

Функция

выражает вычисление байесовского апосте-

риорного распределения

момент

через моменты апосте-

риорного распределения

момент

t —

дисперсии гене-

рирующего процесса.

Теперь рассмотрим генерирующий процесс

множест-

вом состояний, который описывается смесью априорных

(относительно момента

распределений:

(6.10)

где—

вероятность (апостериорная

по

отношению

наблюдению

-i)

того,

что

процесс

мо-

мент

/ —

был в

состоянии

— вектор моментов

1-го

распределения, описы-

вающего состояние

i в

момент

t — 1.

Используя результаты, полученные

для

генерирующего

процесса

одним состоянием,

для

описания каждого

из k

состояний

/ = 1, ..., k по

очереди, получаем:

(6.11)

где s

—

номер состояния

момент

(6.12)

Здесь использована fJ-функция уравнения

(6.9).

Поэтому

полное апостериорное распределение может быть записано

как

(6.13)

где

(

задается уравнением (6.12),

а Р\

—

вероятность

(апостериорная относительно наблюденного значения

)

того,

что

процесс

момент

t —

был в i-u

состоянии

теперь переходит

в /-е

состояние.

Возникает вопрос

о том, как

оценить вероятность пере-

хода

генерирующего процесса

из

состояния

i в

состояние

Рассмотрим проблему

общем виде. Пусть событие

может

наблюдаться лишь

при

условии,

что

произошло какое-ни-

будь

событие

из числа несовместных событий

,...»

142

, вероятности которых известны. События H

обычно

называют гипотезами относительно г. Вероятность реализа-

ции

i-й гипотезы при условии, что наблюдается событие

г, определяется соотношением Байеса:

где Р

(z)

— полная вероятность наступления события г.

Используя

эту формулу в нашем конкретном

случае,

можно получить оценку P\

lt h

следующим образом:

где x(t) - вектор

всех

наблюдений до t включительно;

буква Р обозначает вероятность, буква р - плотность

^Нтомшражении

использовалась функция плотности

вероятности для нормального распределения

а также

то,

что

ИЗ

где Ax

— некоторый отрезок переменной х, содержащий

точку x

в пределах которого плотность распределения

вероятности можно считать постоянной.

Величину К в выражении

(6.14)

можно считать нормали,

зующим

коэффициентом

и найти ее из условия 2

Я}'*

= 1,

что полностью определяет Р}''

и апостериорное распре-

деление (6.13).

Здесь возникает одно серьезное практическое затрудне-

ние.

Начиная с

fc-компоиёнтного

априорного

распределения,

представленного в выражении (6.10), мы приходим

^-ком-

понентному апостериорному распределению в (6.13). Про-

должая этот процесс, мы должны по получении последую-

щих наблюденных значений x

t+1

t+i

..,, переходить

апостериорным распределениям с fe

и т. д. компонен-

тами.

Это

очевидно

неприемлемо

с вычислительной

точки

зре-

ния,

так как требования к

объему

памяти и к машинному

времени становились бы чрезмерными уже после неболь-

ших рядов наблюдений. Поэтому авторы рассматриваемого

метода предлагают некоторые приближения для удержания

требований к ресурсам компьютера в разумных рамках.

Имеется несколько путей уменьшения числа компонент

апостериорного распределения, идин из них заключается

следующем.

Все множество компонент смеси распределений в

(6.13)

с одинаковым текущим состоянием / в целом заменяется

на

единственное двумерное нормальное распределение,

первые и вторые моменты которого

получают

соответствую-

щей процедурой взвешивания, т. е.

(6.15)

где

(6.16')

Выражения для вторых моментов более громоздки.

В качестве примера приведем одно из них:

(6.16")

Рассмотренным способом

удается

сохранить наиболее

ценную информацию о текущем состоянии процесса и

«сжать»

апостериорное распределение (a

1>t

, ß

, t\

в вы

ражении (6.15), приведя его к

тому

же

виду,

что и в выра-

жении

(6.10)

в начале цикла обновления.

Сделаем краткий обзор метода по этапам цикла обнов-

ления.

Эта,л 1. После получения наблюдения

(

пред-

полагается, что апостериорное распределение

является смесью двумерных нормальных распределений:

где как

так и параметры

Q>t-i

известны.

Этап 2. Априорно,-до получения члена *„ пред-

полагается, что процесс в момент t может оказаться

любом

из

возможных состояний, каждое из которых характери-

зуется параметрами:

Г]

— вероятность состояния /;

(

J\ D

{

J\ Di

— дисперсии генерирующего процесса в сос-

тоянии

ппп

Эт а п 3. Рассматривая все возможные переходы про-

цесса из одного состояния в

другое

при

движении от момента

t -

к моменту t и учитывая вероятности этих переходов,

получаем выражение апостериорного распределения через

смесь fe

двумерных распределений:

где

РУ'Н равно выражению (6.14).

145

ЛУЧ1НЯ

ня

Распределении с

компонентами, по-

лученная на предыдущем этапе, сжимается

приближенно

эквивалентное распределение

с k

компонентами:

где Q\

2/f •

параметры Ф\

})

задаются уравнениями

(6.16')

(6.16").

Tor^InJl

Апосте

°Р

нс

распределение теперь имеет

бш-fRKmo^J

И На

Этапе

lj и

сле

ДУ

Щая итерация может

оыть выполнена аналогичным образом.

•

dTan

- Д

ля

получения прогнозов по модели

nDOKCHSSf

6НИЙ

С к

компон

ентами

свою очередь ап-

?n^Sp

amf

ДВумершм

нормальньш распределением

М(

5^1

ХОДИМ0

ать

не

^олько замечаний относительно

пиеГ,™

НИЙ

Mo<Z

(6Л)

ВКЛ1

°чает

сезонные

коэ#и-

циенты как известные (а не как неизвестные, подобно <ht и

äöfi

Раз

меется

модель можно расширить таким образом,

соЙкпГп,°и

НН

Ь1е

КОЭффиЦиентЬ1 0П

РеДелять на той

же

бай^

свя^

ве

'°да

ако

дайте это

не

рекомендуется, так как

DOB

iv/f™

станием числа неизвестных парамет-

ния

б^т

пи

ЛН0Й

ба&

0ВСК0Й

работки сезонного явле-

поiSSSl

ЩК

МаЛ П0

авнен

ию с затратами, особенно

вод состояний"^™

ЧТ

использ

ется

подход

с множест-

HocS°

rpi

y значения

озонных коэффициентов,

в сущ-

ности,

связаны

вращением Земли вокруг Солнца,

то

им

обычно присуща большая стабильность,

чем

уровню

или

коэффициенту

линейного роста. Однако

на

практике

и се-

зонные

факторы подвержены изменениям,

и в

случае

необ-

ходимости

это

предлагается учитывать вне байесовской си-

стемы.

§ 3. РЕАЛИЗАЦИЯ МЕТОДА

Полагаем,

что

дисперсия основной стохастичес-

кой

составляющей процесса

в его

«нормальном» состоянии

(т.

е. при

отсутствии изменений) известна:

Это требование

не

является чрезмерным. Приближен-

ные

значения характеристик основной стохастической ком-

поненты

необходимы

любой задаче практического прогно-

зирования,

байесовская система, как

утверждают

авторы

метода, не боится

даже

больших ошибок

численных оцен-

ках этих значений.

Считаем также,

что к

началу процесса оценки коэффи-

циентов сезонности известны.

общем

случае

как

коэффи-

циенты

сезонности, так

характеристики случайных откло-

нений

можно оценивать посредством предварительного

ана-

лиза, например применением

той или

иной сглаживающей

процедуры

прошлым выборочным данным. При этом,

ко-

нечно,

необходимо особое внимание

искажениям, вноси-

мым самим процессом сглаживания. Иногда

исследовате-

ля

имеется какая-то априорная информация. Тогда ее мож-

но

использовать непосредственно вместо анализа прошлых

Данных или

дополнение

нему.

должны быть заданы остальные параметры систе-

мы:

—

количество состояний процесса;

—

вероятность наступления состояния

—

дисперсии стохастических компонент,

ха-

рактеризующие состояние

На

практике удобно определять эти дисперсии

в еди-

ницах дисперсии основных флуктуации

следующим

образом:

147

10*

Выбор значений параметров

Как

отмечалось в § 1,

будем

различать четыре основные

ситуации:

отсутствие

изменений,

ступенчатое

изменение,

из-

менение

коэффициенте

линейного

роста, случайное импуль-

сное

отклонение,

т. е. речь

идет

четырех

состояниях про-

цесса, но если необходимо различать степени

изменений,

то

их число может быть и большим.

Авторы

метода считают,

однако,

что четыре

состояния

системы

дают

хорошие резуль-

таты и нет необходимости вводить более тонкие различия.

Таким

образом, они

берут

k — 4.

Что касается остальных параметров, то при испытаниях

большим числом их различных численных значений авто-

рами

метода был сделан вывод о

том,

что работа системы

ма-

ло чувствительна к значениям параметров, если при их вы-

боре соблюдаются

некоторые

правила:

1. Состоянию

«отсутствия

изменений» приписывается

высокая

вероятность.

2. Состояние

«ступенчатое

изменение» должно характе-

ризоваться большим значением R

и очень малой вероят-

ностью.

3. Состояние «изменение в

коэффициенте

линейного рос-

та» должно иметь или a) R

<С

и Т

же

вероятность, что

состояние

«ступенчатое

изменение», или б) R„ = R

намного

меньшую вероятность, чем вероятность

«ступенча-

того изменения».

4. Вероятность

«случайного

импульса»

должна быть по

крайней

мере в 10 раз больше, чем вероятность «ступенчато-

го изменения» или «изменения в коэффициенте линейного

роста».

5. Сумма относительных

коэффициентов

R, -f R

-Ь Re

для состояния

«случайного

импульса»

должны быть не мень-

ше,

чем соответствующая сумма для любого

другого

состоя-

ния.

Условие (1) является гипотезой того, что «нормальное»

течение процесса лишь изредка прерывается скачкообраз-

ными

изменениями в уровне или коэффициенте линейного

роста.

Эффект

условия (2) и (4) состоит в том, что получение

первой

большой ошибки

будет

рассматриваться системой

как

случайный импульс до тех пор, пока последующие

дан-

ные

не подтвердят, что произошло ступенчатое изменение

уровня или коэффициента линейного роста.

148

Следствием условия

(3)

является

то, что

система стано-

вится

менее чувствительной

изменениям

коэффициенте

линейного

роста,

чем

уровне.

Во

многих практических

ситуациях

это

свойство желательно:

оно

предотвращает

«раскачку»

системы.

Условие

(5)

обеспечивает более широкий диапазон

ам-

плитуд состоянию случайного импульсного возмущения.

табл.

6.2

представлен рекомендуемый авторами метода

набор

значений параметров, удовлетворяющих перечислен-

ным

требованиям; этот набор давал

них

хорошие резуль-

таты

при

проверке

на

искусственных

реальных данных.

Таблица 6.2

Рекомендуемые

значения параметров (ft=4)

Несмотря на то что до сих пор речь шла о н^отоРМ

ле различных состояний

известными f

СТ0ЯН

™Д

ge-

ностями

их

наступления, нет оснований считать чтсгэти

ве

роятности неизменны

во

времени. Поэтому

в <*^ <**£

метода иногда целесообразно включать

ту ^

WJrSSS

дуру

модификации первоначально

за

анных

*^°f

НОСТ

состояний

учетом фактических входных данных.

ного роста величиной

1<т. пппгнозы на один

На

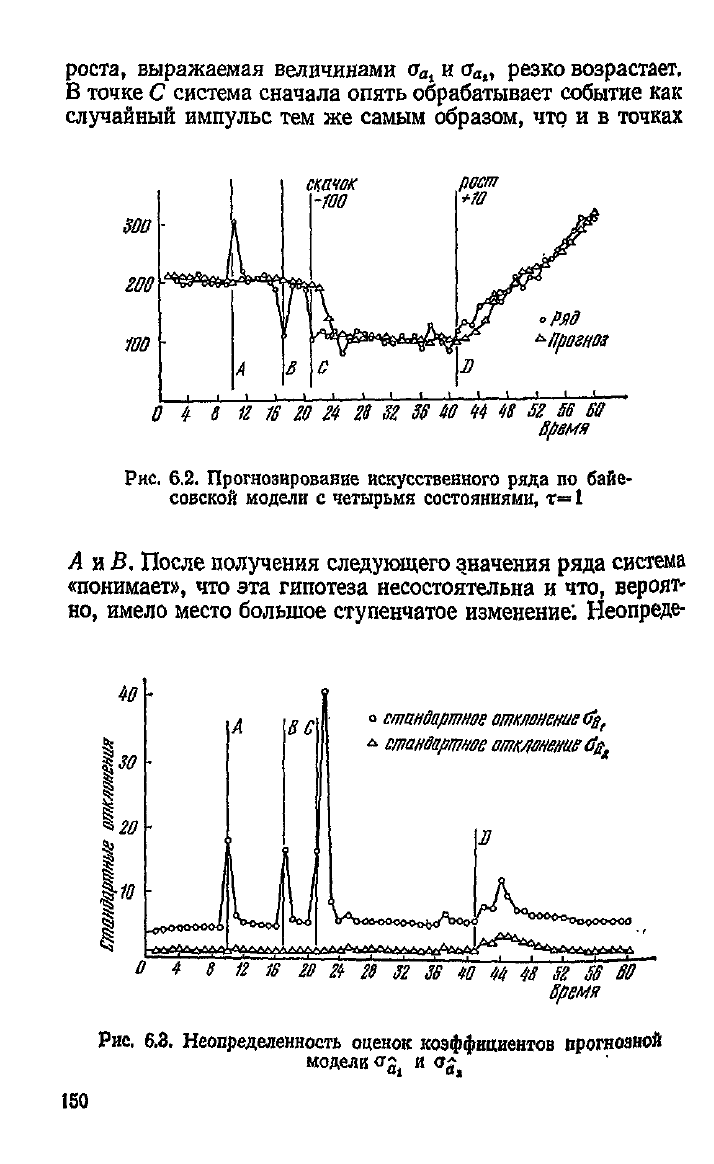
рис.

6.2

представлены данные

иоД««

™ °^

шаг вперед. Видно, что случайным^^^ SpSTa.

дает

очень малый вес

при

формировании текущего

пр

Рис.

6.3

показывает,

что ™

f™™°™

™Smro

носительно значений уровня

коэ#ициента линейно

Состояние

Изменения

отсутствуют

Ступенчатое

изменение

Изменение

коэффициента

ного

роста

Случайное

импульсное

нение

линей-

откло-

Вероятность

0,900

0,003

0,094

101

Я«

100

роста, выражаемая величинами о

а%

о*

„

резко возрастает.

В точке

система сначала опять обрабатывает событие как

случайный импульс тем

же

самым образом, что

и в

точках

Рис.

6.2. Прогнозирование искусственного ряда по байе-

совской модели с четырьмя состояниями, т=

В.

После получения

следующего

значения ряда система

«понимает», что эта гипотеза несостоятельна

что, вероят-

но,

имело место большое ступенчатое изменение; Неопреде-

Рис.

6.3. Неопределенность оценок коэффициентов прогнозной

модели ст^ и о^

150