Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

Приравнивая

коэффициенты при одинаковых степенях

В слева и справа, получаем:

где Для / <

tyi '=

и для / > (f Q

}

= 0.

Таким

обр'азом,'

коэффициенты'^

легко подсчитываются

рекурсивно.

Тогда

прогноз с вероятностью 1 — v не

будет

выходить за пределы

т№'Щ/2

является квантилем уровня 1 — v/2 стандартного

нормального

.распределения.,

Это

величина табличная:

1-V

"v/2

бОО/

0,674

95%

1,96

Адаптивные свойства модели. Рассмот-

рим

модель

V#t =

—

QB)e

момент

t + т она

может

быть записана:

Верем

условное математическое ожидание

момент

if при

известном до момента

прошлом.

Учитывая, что

получаем

(7.46)

191

Используя тот факт, что x

— x

(t— 1) + e

(7.46)

мож-

но

записать в виде х

(t) — ~x

(t — 1) -f

где X =

— 1 — Q или в виде х

(t) — hx

+ (1 — К)х

it — 1), что

является обычной моделью экспоненциальной средней

(см.

гл. 1), которая может быть записана и так:

где

lit

— экспоненциальная средняя процесса в момент /;

lit

— адаптивный коэффициент.

Можно

также показать, что предиктор процесса

приводится к модели линейного роста экспоненциального

типа:

Когда х

(t) рассматривается как функция от т при фик-

сированном

будем

называть ее прогнозирующей функцией

для момента t. Общий процесс (0, d, q) имеет своей прогно-

зирующей функцией полином от х степени d — 1.

(7.47)

для х > q — d.

Коэффициенты

iit

должны последовательно обновлять-

ся

с получением каждой новой фактической точки. Для t <•

<<7

— d прогноз

будет

зависеть от г

_i, ....

Bt~q+x>

а после этого определяться полиномом (7.47).

Класс

функций прогноза. Посмотрим,

какими

еще функциями можно описать

будущее

поведение

ряда исходя из модели АРИСС.

При

прогнозировании процесса

будущие

значения 8 являются неизвестными и непредсказуе-

мыми,

поэтому заменим их при вычислении прогнозов нулем.

Тогда класс функций прогноза для т > q

будет

определяться

192

общим решением однородного линейного разностного урав-

нения:

(7.48)

где

(7.49)

Предположим сначала, что G

, ..., G

> различны.

Тогда общее решение для момента k при условии, что ряд

начинается в момент t (при прогнозировании / соответствует

текущему моменту времени),

будет:

гдеЛ{

— константы. В этом можно убедиться непосредствен-

ной

подстановкой в исходное уравнение. Тогда при выпол-

нении

условия стационарности | G

| < 1 действительный

корень

уравнения ¥ (В) = 0 даст в качестве слагаемого за-

тухающую

экспоненту G/~"'. Пара комплексных корней

дает

затухающую

синусоидальную волну:

Предположим теперь, что ¥ (В) = 0 имеет т равных

корней

Gö

, так что И (В) содержит множитель (1 —

Тогда подстановкой можно проверить, что общее решение

будет:

В частности, при G

— 1 получаем полином от k — t поряд-

ка m—'l.

Вообще , когда ¥ (В) раскладывается на множители как

B)(l -

ß)...(l

B)(\

)

общее решение

будет:

т. е. функция прогнозирования состоит из смеси затухающих

экспонент,

полиномиальных членов, затухающих синусои-

дальных волн и их комбинаций.

Если взять комплексные корни характеристического

Уравнения на границе стационарности |Gj| — 1, то модель

193

превращается в нестационарнуюивключаетрегулярные(не-

затухающие)

периодические

колебания.

Например, функция

прогноза, которая является синусоидальной волной с 12-.

точечным периодом,

будет

удовлетворять уравнению:

где оператор В относится к т.

Это означает, что модель Брауна по своей

структуре

функциям

прогнозирования является частным

случаем

мо-

дели

АРИСС.

Модель Брауна является более жесткой и при

заданном наборе

функций,

включенных в нее, процесс про-

гнозирования полностью определяется единственным пара-

метром ß, который, кстати сказать, часто задается интуитив-

но,

Поэтому для обработки протяженных рядов предпочти-

тельней использовать метод Бокса-Дженкинса. Однако при

небольшом количестве точек, когда этот метод бессилен, мо-

дель

Брауна может оказаться полезной. Подбирать какие-

либо сложные функции при малом объеме выборки нецеле-

сообразно, поэтому для практического применения из

всех

моделей Брауна имеет смысл оставить лишь самые простые.

В экономических исследованиях включение в модель

синусоид,

даже

с адаптивной фазой и амплитудой, редко

приводит к удовлетворительному отображению сезонных

колебаний, и в каждом

случае

требуется

дополнительный

анализ.

Если включение синусоиды все же оказывается

полезным, то

удобнее

проводить исследование по модели

АРЙСС

для преобразованного ряда. Например, при 12-

точечном периоде целесообразно перейти к анализу ряда

щ.

_ узв + B

и т. п'.

Для более качественного анализа сезонных явлении

Бокс

и Дженкинс в [5] предлагают специальную

схему.

Учитывая, что в ней используются уже рассмотренные на-

ми

принципы

процедуры,

не

будем

на этом останавливать-

ся.

Сравнение процесса АРИСС с процессом Тейла—-Вейджа

Процесс Тейла—Вейджа можно записать как

(7.50)

где и и v — независимые случайные переменные. Посмот-

рим,

не является ли этот процесс частным

случаем

процес-

сов класса АРИСС. Для достижения стационарности не-

194

обходимо бзять вторую разность от исходного ряда х, т.«.

d — 2. Автокорреляционная функция для вторых разностей

соответствии с (1.5) обрывается при лаге k ~ 3. Поэтому

среди процессов

АРИСС

адекватными процессу Тейла—Вей-

джа могут оказаться только те, которые имеют порядок

(О,

2, 2), т. е.

(7.51)

Предположим,

что (7.50) может быть эквивалентно пред-

ставлен процессом (7.51). Тогда имеем соотношение

(7.52)

Рассмотрим

условные математические ожидания. По

Вычтем (7.54) из (7.53) — 2щ~

—

„

(7.55)

(7.53) из (7.52)

+ щ — 8

(

. (7.56)

Тогда связь между е* и щ, v

по (7.56)

будет

ej = и» + fj»

по (7.55) е, =.-|^«/.

Это приводит к соотношениям:

или

Таким

образом, гипотеза адекватности

двух

рассмат-

риваемых процессов приводит

тому,

что два независимых

ст

ти

ческих

процесса

выражаются один через дру-

гой. Это противоречие не устранимо ни при каких значениях

4i. Следовательно, процесс Тейла—Вейджа нельзя привес-

ти

процессу АРИСС

одним источником белого шума.

195

§ 4. ПРОГНОЗИРОВАНИЕ ПОСЛЕ

ЛОГАРИФМИЧЕСКОГО

ПРЕОБРАЗОВАНИЯ

В экономике часто встречаются негомогениые

временные ряды, в которых рост в процентном измерении

представляет, однако, гомогенный процесс. В этих

случаях

обычно переходят от исходного неоднородного ряда к на-

туральным логарифмам. Если к преобразованному ряду по-

добрать модель АРИСС, то прогнозы, генерированные

этой

моделью,

будут,

конечно, прогнозами логарифмов

будущих

наблюдений. Представляется естественным об-

ратный

переход

от логарифмов к исходному представлению

операцией антилсгарифмирования полученного прогноза.

Но

даст

ли такая операция условное математическое ожи-

дание

будущего

значения исходного ряда?

Ответ

будет

от-

рицательным, так как если обозначить исходный ряд че-

рез x

, a In (x

) — через у

предложенная операция бу-

дет давать оценку ехр [М (y

+JX)), где X — совокупность

прошлых значений х, а это, вообще гооворя, не является

математическим ожиданием.

Прежде чем продолжить рассуждения, рассмотрим лог-

нормальное распределение [86].

Пусть у — случайная переменная с нормальным' рас-

пределением N (|и, о

) и х — случайная переменная, свя-

занная

с у соотношением х =

&>.

Тогда распределение х

описывается логнормальной функцией плотности:

где х принимает только положительные значения и при

= 0 р (х) — 0. Мода распределения

будет

в точке х рав-

на

е»~

\ а медиана

точке х равна е». Моменты относи-

тельно начала отсчета:

Отсюда

математическое ожидание

а дисперсия

196

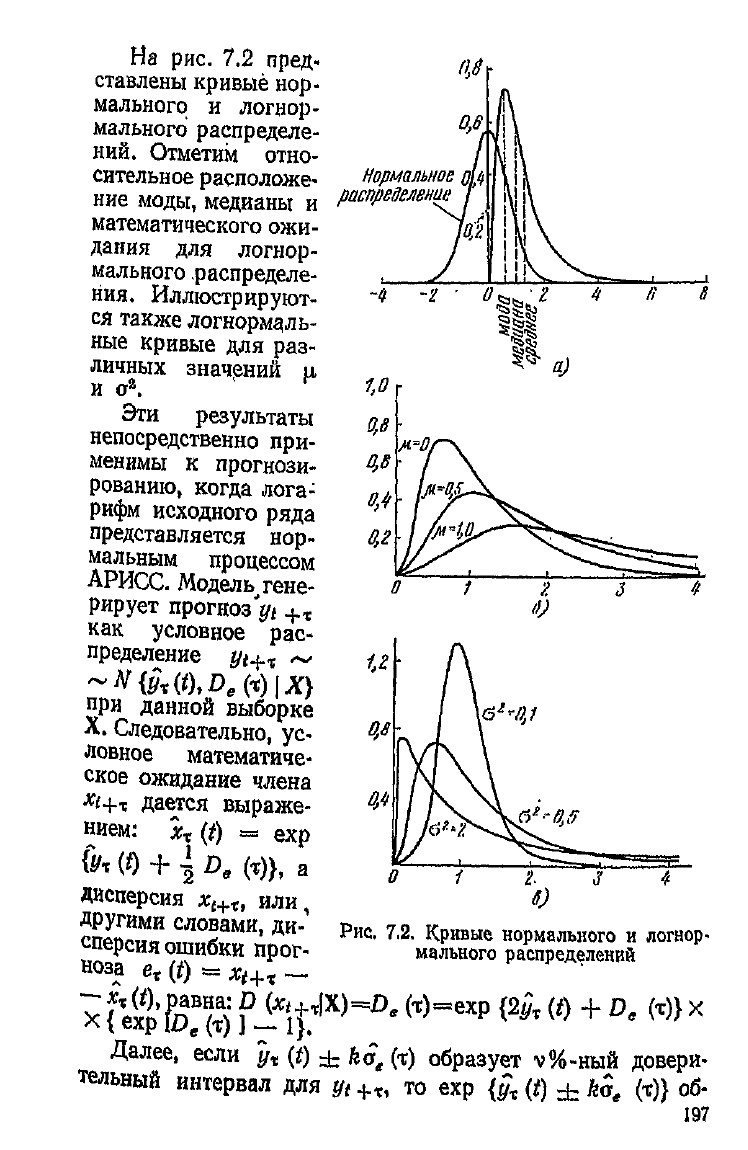
На

рис. 7.2 пред-

ставлены кривые нор-

мального и логнор-

мального распределе-

ний.

Отметим отно-

сительное расположе-

ние

моды, медианы и

математического ожи-

дания

для логнор-

мального.распределе-

ния.

Иллюстрируют-

ся

также логнормаль-

ные кривые для раз-

личных значений и

ЭТИ

результаты

непосредственно при-

менимы к прогнози-

рованию, когда лога-

рифм

исходного ряда

представляется нор-

мальным процессом

АРИСС.

Модель,

гене-

рирует прогноз V*

+-С

как

условное рас-

пределение yt+x ~

~N{y

(t),D

(t)\X}

при

данной выборке

X. Следовательно, ус-

ловное математиче-

ское ожидание члена

xt+x дается выраже-

нием:

(t) — ехр

ft*

(т)},

Дисперсия

t+x

или,

Другими словами, ди-

сперсия

ошибки

прог-

ноза

(0=*и-т

Рис.

7.2. Кривые нормального и логнор-

мального

распределений

fexp

КП")

1Х)==Г)

(t)==ex

{** W +

Далее, если

(t)±ka

(x)

образует

V%-HHU

довери

тельный интервал для y

t +т

, то ехр {^

(t) ± ka

(t)} об

197

разует

v%-Hbifi

доверительный интервал для

*<+*.

Заме-

тим, что доверительный интервал для Xt+

несимметричен

относительно х

(f), в то время как для yt+

он симметри-

чен.

§ 5. АГРЕГИРОВАНИЕ РЯДОВ И МОДЕЛЕЙ

Со

времени введения Дж. Э. Юлом

(1921)

авто-

регрессионных моделей и моделей скользящего среднего

они

вызывают интерес у статистиков, занимающихся анализом

временных рядов. Это объясняется тем, что модели доста-

точно просты и

могут

успешно применяться на практике.

Очевидным обобщением этих моделей является смешанная

модель авторегрессии — скользящего среднего. На прак-

тике смешанную модель АРСС

труднее

оценивать, чем, на-

пример,

AP-модель, но, с

другой

стороны, смешанная мо-

дель может быть статистически более

эффективной,

чем АР-

или

СС-модели. Согласно Боксу и Дженкинсу, если оце-

ниваются одновременно две модели АР (р) и АРСС (p

, q'),

то,

как правило, во второй модели потребуется меньше па-

раметров для достижения удовлетворительных

результа-

тов, т. е. р' + q' < р. Так как имеются веские основания

отдать

предпочтение модели с наименьшим числом парамет-

ров,

то смешанная модель часто предпочтительнее.

В работе К. Гренджера и М. Морриса [62] проведен тео-

ретический анализ, на основе которого сделан вывод о воз-

можности появления смешанных моделей в

результате

аг-

регирования рядов со сравнительно простой структурой.

Основная

теорема, доказанная в этой работе, формулиру-

ется следующим образом.

Пусть x

и y

— два независимых стационарных ряда

с нулевым математическим ожиданием. Тогда если x

~ АРСС (р, т), t/t ~ АРСС

(q,

п) и z

= x

+ Уи

т0 z

-АРСС (г, в), т. е. АРСС (р,

/n)+APCC,

(q, n) =

АРСС (г, s), где г < р + q и й < max (р -Ь п, q + m).

В тех

случаях,

когда два независимых ряда описыва^

ются моделями АРИСС, теорема

утверждает,

что АРИСС

(Рь <k, q

) + АРИСС (p

, d

д»)

« АРИСС (г; d\ s),

198

Не

составляет трудности обобщить основную теорему на

случай суммы любого числа независимых рядов:

где

точки зрения интерпретации два случая представляют

особый интерес. Первый, когда ряды агрегируются и обра-

зуется один общий; большинство макроэкономических ря-

дов, таких, как валовой национальный продукт, экспорт и

т. д., являются агрегатными. Второй, когда наблюденный

ряд является суммой

истинного,

процесса и ошибки наблют

дения:

«сигнал плюс

шум»,

фактически любой макроэко-

номический

ряд содержит существенные ошибки наблюде-

ния.

Рассмотрим несколько частных случаев, полнее раскры-

вающих содержание основной теоремы.

1. АР (р) + белый шум — АРСС (/?, р).

Это

соответствует

наблюдению авторегрессионного про-

цесса в присутствии белого шума.

2. АР (р) + АР (?) = АРСС (р + ft max (p, q))

и,

в частности,

АР (1) + АР (1) = АРСС (2, 1).

Это может соответствовать ситуации, когда исследуемый

ряд является агрегатом

двух

независимых ' авторегрессион-

ных рядов, или случаю, когда процесс АР (р) искажается

ошибкой

наблюдения АР (q).

Отметим,

что

сумма к

рядов,

описываемых моделью АР(1).

приводит к модели АРСС (к, к — 1).

СС

(р) + СС

(q)

= СС ( max (p, q))

и,

в частности, СС (р) + белый шум = СС (р).

Таким

образом, если истинный процесс генерируется

моделью

СС,

то добавление белого шума ошибок наблюде-

ния

не изменит типа и порядка модели. Значения парамет-

ров при этом, конечно, изменятся.

4. АРСС (р, т) -j-белый шум =

(АРСС

(р,р)>

если р >

т\

\APCC

(р,

т),

если р < т

199

Это говорит о том, что добавление ошибки наблюдения

может изменить порядок модели АРСС,

хотя

и не обяза-

тельно.

5. АР (р) + СС (?) = АРСС (р, р + q).

Этот случай также можно интерпретировать либо как

агрегирование, либо как наложение ошибки наблюдения,

не

являющейся белым шумом.

Итак,

четырех

из пяти рассмотренных случаев, кроме

случая 3, после сложения независимых рядов были полу-

чены смешанные модели авторегрессии — скользящего сред-

него. Между тем требование независимости рядов может

быть несколько ослаблено и получены те же выводы. Пред-

положим, что каждый ряд, входящий в

агрегат,

состоит из

двух

компонент. Одна компонента, общая для

всех

рядов,

представляет влияние общеэкономических факторов, а дру-

гая не зависит от первой и характерна только для данного

ряда. Тогда для каждой компоненты

могут

быть приняты

простые модели, а после агрегирования получена общая

модель суммы рядов в соответствии с основной теоремой.

Такие модели успешно использовались за

рубежом

при ана-

лизе цен на фондовой бирже и

доходов

фирм.

Наконец,

рассмотрим еще один случай, когда x

и y

ге-

нерированы авторегрессионной схемой

двух

переменных с

обратной

связью

a (B)x

-f Ь (B)y

= г

(B)x

(В)у^Щ>

где &

, щ — некоррелированные белые шумы;

Ь (0) - с (0)

Модель, описывающая только х

определяется элими-

нированием y

и имеет вид: [a (B)d (В) — с (В)Ь (В) ]x

d (B)e

+ b (B)u

Таким

образом, вновь появляется модель АРСС (р,ф

легко показать, что вообще р> q.

Рассмотренные случаи говорят о том, что по-видимому,

многие реальные данные описываются моделью АРСС. Фак-

тически можно сделать вывод, что наиболее вероятной мо-

делью

на практике

будет

смешанная модель авторегрессии —

скользящего среднего, что надо учитывать на стадии иден-

тификации.

§ 6. .ПРИМЕРЫ

Метод Бокса и Дженкинса был испытан на рядах

курса акций фирмы ИБМ и цен на золото.

Ряд

ИБМ

также был разделен на 3 отрезка по 48 точек,

а ряд цен на золото — на 6 отрезков по 60 точек. Для каж-

200