Лесникова Н.П. Физическая химия. Самостоятельное решение задач по химической термодинамике, электрохимии и кинетике

Подождите немного. Документ загружается.

161

Интегрирование уравнения (3.15) в соответствующих преде-

лах, позволяет получить выражение константы скорости для реак-

ции первого порядка:





 

.ln

,lnln

,ln,

ktkxaa

tkxadtk

xad















(3.16)

Из уравнения константы скорости для реакции первого поряд-

ка получим зависимость концентрации реагентов и продуктов реак-

ции от времени:

























,exp1,exp

ecc

ktaxPktaxaA

















(3.17)

Следует отметить, что константа скорости реакции первого по-

рядка может быть определена и в том случае, если вместо концен-

трации реагента измерять какое либо свойство системы. например,

оптическую плотность.

Из закона Бугера-Ламберта-Беера оптическую плотность (Е) и,

соответственно, концентрацию реагента в различные моменты вре-

мени можно представить

..,

,000

cclEclE

AtAtt





Подставим полученные значения концентрации вещества А в

уравнение константы скорости реакции первого порядка (3.16).

.ln

tAt

txc

txa

k 









(3.18)

Если предположить, что за некоторый промежуток времени













t концентрация реагентов уменьшилась в два раза, то выраже-

ние константы скорости реакции (3.16) после соответствующих пре-

образований принимает вид:

 

2ln

;

2ln

;ln

;

ktt

xa 





(3.19)

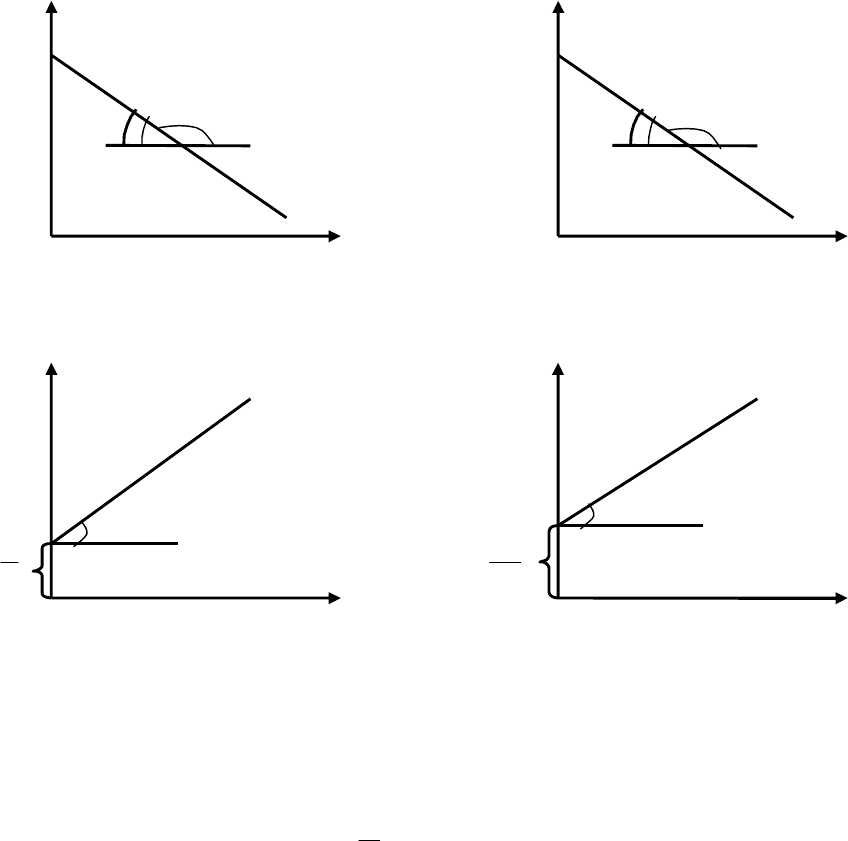
162

Графическое изображение функциональной зависимости





xaC



ln от времени соответствует рис. 3.2.(б).

Тангенс угла наклона прямой (а, б) позволяет определить кон-

станту скорости: .

tgk 



Реакции второго порядка. Многие бимолекулярные реакции

являются реакциями второго порядка, для которых возможны три

следующие схемы элементарного механизма превращения реагентов

в продукты реакции:









   

,2)

BAPBAc

PAb

BAPBAa











(3.20)

Выведем кинетические уравнения для всех типов реакций вто-

рого порядка. Предположим, что реакция протекает по механизму,

представленному первой схемой с равными концентрациями реаген-







tgtgk



















tgtgk











 xa

ktg











 xa

2ktg





Рис. 3.2. Графический способ определения порядка реакции:

а – при n = 0; б – при n = 1; в – при n = 2; г – при n = 3







163

тов. Тогда, в любой момент времени протекания реакции, концен-

трации реагентов соответствуют значениям:









   

 

xacBA

acBA





Подставим эти выражения в уравнение скорости реакции (3.8), ко-

торое для реакций второго порядка принимает вид:

 

xak

W 

Разделим переменные в полученном уравнении и проинтегрируем

его в соответствующих пределах:

 





 

dtk

xad

dtk

xad

илиdtk





















Тогда,

111111































cctaxat

k (3.21)

Если в какой-то промежуток времени протекания реакции













t концентрация любого из реагентов уменьшится в два раза, т.е.



то уравнение константы скорости (3.21) принимает

вид

ata

k 













 (3.22)

Графическое изображение функциональной зависимости 1/с от вре-

мени показано на рис. 3.2.(в), из которого следует, что





Если реакция второго порядка протекает по второй схеме, то

концентрация реагента А в любой момент времени равна (а – 2х).

После подстановки этого значения в уравнение основного закона

кинетики (3.8) и его интегрирования в соответствующих пределах,

получим:

164

 





 



































axat

ktk

axa

dtk

xad

dtk

xak

(3.23)

Если концентрация вещества А равна









cxaA







2 , т.е.

текущей концентрации, то уравнение константы скорости (3.23)

становится аналогичным уравнению (3.21). Но на графике функцио-

нальной зависимости 1/с от времени





При протекании реакции по третьей схеме концентрации реа-

гентов не равны между собой. Выразим концентрации реагентов

следующим образом:

























.;);(

,0,0

xPxcxbBxcxaA



















Подставим в уравнение основного постулата кинетики (3.8) эти

выражения и разделим переменные:

  

,0,0

dtk

xcxc

xcxck





 (3.24)

Для дальнейшего вывода используем разложение сложной дроби на

две простые, что можно представить следующим образом:

        

1111



















 xbxaabxbxa

Тогда уравнение (3.24) принимает вид

 

     

,0,0,0,0

,0,0

dtk

BAAB



































(3.25)

Интегрирование этого выражения в пределах от х = 0 до х и от

t = 0 до t с последующим преобразованием полученного логарифми-

ческого уравнения

 

   





,lnlnlnln

,0,0.0,0

,0,0

tkcxccxc

BBAA





(3.26)

позволяет получить выражение константы скорости реакции второго

порядка, когда концентрации реагентов не равны между собой:

165

 





 

.ln

,0,0

xcc

cct





(3.27)

Реакции n-порядка. Для вывода кинетического уравнения кон-

станты скорости реакции любого порядка, кроме п = 1, разделим в

уравнении (3.8) переменные и проинтегрируем полученное выраже-

ние в соответствующих пределах:

 

dtk

xad

dtk

xad

dtk

xak













































Математические преобразования позволяют получить уравне-

ние, которое является общим для реакций любого порядка, кроме

п = 1 и которое справедливо, если концентрации реагентов равны

между собой:

 

















 nn

k (3.28)

Предположим, что к моменту времени

концентрация реа-

гентов уменьшится вдвое, тогда константа скорости будет равна:

 





























k (3.29)

Из этого уравнения (3.29) выражение времени

для реакций раз-

личных порядков, кроме первого имеет вид:









t (3.30)

3.3. Способы определения порядка реакции

Основными способами определения порядка реакции являют-

ся: интегральный, дифференциальный и метод изолирования Ост-

вальда.

166

Интегральные методы определения порядков реакций осно-

ваны на применении интегрального кинетического уравнения для

обработки первичных экспериментальных результатов концентра-

ция – время.

Метод подстановки. Позволяет установить соответствие

опытных данных одному из интегральных кинетических уравнений.

Соответствие установлено, если после подстановки опытных дан-

ных об изменении концентрации от времени в очередные кинетиче-

ские уравнения, рассчитанные значения константы скорости колеб-

лются около постоянной величины. Этот способ дает надежные ре-

зультаты для реакций, степень превращения в которых достигает 70

– 90%.

Несовпадающие значения константы указывают, что реакция

сложная, а порядок может быть дробным или отрицательным. Сле-

довательно, надо искать другой способ определения порядка реак-

ции.

Вариантом метода подстановки является графический способ.

В этом случае порядок соответствует той величине, на каком из гра-

фиков наблюдается линейная функциональная зависимость концен-

трации от времени.

Определение порядка реакции по времени полупревращения. По

этому способу можно определить любой порядок реакции, если

имеются для различных опытов данные о начальных значениях кон-

центрации реагентов и времени, когда их концентрация уменьши-

лась вдвое. Уравнение для определения порядка реакции выводится

после соответствующего преобразования соотношения (3.30).

Прологарифмируем уравнение (3.30), при этом предположим,

что для данной реакции порядок реакции и константа скорости яв-

ляются величинами постоянными:









 

.,,

,ln1lnln

,ln1

lnln

constknесли

AгдеanAt











































(3.31)

167

Пусть из опытных данных значение

 

t соответствует на-

чальной концентрации

 

, а значение

 

t соответствует началь-

ной концентрации

 

, тогда

 





 

.ln1lnln

,ln1lnln

cnAt







(3.32)

Приравняем из обоих уравнений выражение ln A и преобразуем по-

лученное соотношение:

 





 





 

,ln1lnln1ln

110

cntcnt















   





   

.lnlnlnln1

12010

ttccn







Тогда порядок реакции можно определить из уравнения:

   

 

lnln

2010





















n (3.33)

Разновидностью этого способа является графическое изобра-

жение ln t

1/2

от ln c

. Если соблюдается линейная зависимость этих

величин, то угол наклона позволяет также определить порядок реак-

ции:









ntg



Метод Оствальда – Нойесса. Этот метод основан на зависи-

мости времени превращения

исходного вещества на определен-

ную долю от начальной концентрации. Из уравнения (3.30) для ре-

акций п – порядка при любом значении х можно получить следую-

щие уравнения:

 













 

11/112











t (3.34)

Если в уравнение (3.34) подставить вместо х величины

;

aaa

то получим ряд выражений времени превращения

для реакций

различных порядков:

168

Время превращения

порядок

реакции

1/2

1/3

1/4

 

121







 







 



Достоинство всех интегральных способов определения порядка

реакции в том, что они позволяют использовать первичные данные:

концентрация – время.

Дифференциальный метод определения порядка реакции.

Этот метод, который иногда называют методом Вант – Гоффа, осно-

ван на использовании основного кинетического уравнения

ckW  . Метод позволяет достаточно точно определить порядок

реакции, если имеются достоверные значения скорости реакции при

различных концентрациях c

Уравнение для определения порядка реакции может быть по-

лучено следующим образом:

.lnlnln;lnlnln

,,lnlnln

cnkWcnkW

тогдаcnkWckW





Так как константа скорости в этих реакциях имеет одинаковое зна-

чение, то из полученного равенства скоростей порядок реакции

можно определить по уравнению

lnln

,lnlnlnln

2211

cnWcnW











(3.35)

169

Графическое решение уравнения (3.35) в координатах

от

имеет вид прямой, где n

tg 



Метод изолирования Оствальда. Определяется частный по-

рядок реакции по каждому веществу, участвующему в реакции. Об-

щий порядок реакции равен сумме частных порядков. Для опреде-

ления частного порядка реакции все реагенты берутся в избытке, а

то вещество, по которому определяется порядок реакции – в недос-

татке. Выражение скорости реакции при [B] >> [A] соответствует

выражению (3.36), при этом, величина кажущейся константы скоро-

сти, зависит от концентрации вещества В. Порядок реакции по ве-

ществу А находят одним из рассмотренных выше способов.

каж

ckkгдеckW  (3.36)

Затем при постоянной температуре и различных значениях [B]

причем,{[B]

>> [A]

, определяется численное значение k

каж

. Гра-

фическим или алгебраическим путем рассчитывается порядок реак-

ции по веществу В (n

) и константа скорости k по уравнению ln

каж

= ln k + n

[B]. Зная порядки реакции по отдельным веществам

(частные порядки реакции), находят общий порядок реакции (n = n

+ n

3.4. Зависимость скорости реакции от температуры.

Вывод и анализ уравнения Аррениуса.

Для большинства химических реакций (исключая тримолеку-

лярные и ферментативные) скорость реакции с ростом температуры

увеличивается. Изменение скорости от температуры возможно в ре-

зультате изменения трех величин: константы скорости, концентра-

ции и порядка реакции. Обычно концентрация реагентов (особенно

для реакций в жидкой фазе) изменяется с температурой незначи-

тельно. Изменение порядка реакции под влиянием температуры –

явление редкое. Поэтому, в химической кинетике изменение скоро-

сти реакции под влиянием температуры связано, в первую очередь, с

изменением константы скорости.

Для многих реакций, особенно для реакций в растворах, дли-

тельное время было справедливым правило Вант – Гоффа, из ко-

торого следовало: "При повышении температуры на десять гра-

дусов скорость реакции увеличивается в два – четыре раза".

170

,,42

1010

тогда

или













(3.37)

По физическому смыслу величину γ считают температурным

коэффициентом Вант – Гоффа. На практике в значениях этого ко-

эффициента имелись значительные отклонения от предела два – че-

тыре раза.

Аррениус внес соответствующие допущения, которые допол-

нили правило Вант – Гоффа и позволили более точно установить за-

висимость скорости реакции от температуры.

Реагировать могут не все молекулы, но лишь те, которые

находятся в особой таутомерной форме или активной модифи-

кации. Эта активная, способная к реакции форма молекул, образу-

ется из обычных нормальных молекул при поглощении теплоты









молькДжE /



. Тогда, схему элементарной реакции следует пред-

ставить в виде:

constE













Лимитирующей стадией, определяющей скорость реакции, яв-

ляется первая, которая протекает значительно медленнее второй ста-

дии.

Образование активной модификации является обратимой ре-

акцией. Это позволяет концентрацию активной модификации выра-

зить через константу равновесия K

Введем соответствующие обозначения:



cc , – концентра-

ции исходного реагента А и его активной модификации. Тогда из

основного постулата кинетики, скорость реакции представим в виде

(согласно схеме реакции):

 

cKconstcconst

cKc









(3.38)