Лекции - Уравнения в частных производных
Подождите немного. Документ загружается.

www.uchites.ru
1
Уравнения в частных производных
Лекции
U§ 1. Некоторые определения и обозначения.
Определение.
Дифференциальным уравнением называется уравнение, содержащее производные
неизвестной функции. Если неизвестная функция зависит от одной переменной, то это
обыкновенное дифференциальное уравнение, иначе - уравнение в частных производных.
Определение.
Наивысший порядок производных неизвестной функции, входящих в уравнение, называется
порядком уравнения.
Определение.
Дифференциальное уравнение называется линейным, если производные и сама неизвестная
функция входят
в уравнение линейным образом.
a x u x a x u x ax ux f x
ij x x
ij
n
ix
i
n
ij i
() () () () ()() ()
,
++=
==
∑∑
11
(1)
Пусть выбран любой
α
α
α
= ( ,..., )
1 n
, где
α
α
ii
Z≥
∈
0, , и его норма:
α
α
α
∂
∂
∂
∂
α
αα
=++
=
F
H
G
I
K
J
F
H
G
I
K
J
1
1
1
... ,
...
n
n
D
xx
n
- дифференциальный оператор.
axDux fx
α
α
α
() () ()=
≤
∑
2
- запись линейного диф. уравнения с помощью диф. оператора.
(2)
Определение.
Открытое, связное множество
QR
n
⊂ называется областью.
По умолчанию будем считать область ограниченной.
Через
∂
Q или Γ будем обозначать границу области.
Определение.
S
R
n
⊂ - (n-1)-мерное многообразие S в
R
n
принадлежит классу
C
k
(k ≥ 0), если
для
∀∈∃>xSr
0
0, и 1 ≤≤in такие, что:
SSx x xx D
ri
I () (),
0
==
′′
∈
ϕ
lq
, где
′
=
−
+
xx xx x
ii n
( ,..., , ,..., )
111
SSx
r
I ()
0
однозначно проектируется на плоскость x
i
=
0
lq
, при этом:
D - проекция данного множества на плоскость
x
i
=
0
lq
,
ϕ
- k раз непрерывно
дифференцируема в D по всем переменным.

www.uchites.ru
2
Можно разбить поверхность на части, в каждой части можно одну координату выразить
через другие непрерывно дифференцируемой функцией.
C
Q
k
() - множество k раз непрерывно дифференцируемых функций в Q.
C
Q
k
() - множество k раз непрерывно дифференцируемых функций в Q .
C
QCQ
i
i
∞
=
∞
=() ()
0
I
, аналогично
C
Q
∞
().
&
()
C
Q
k
- множество финитных k раз непрерывно дифференцируемых функций.
Аналогично:
&
()
C
Q
∞
.
U§ 2. Классификация линейных уравнений в частных
производных второго порядка.
a x u x a x u x ax ux f x
ij x x
ij
n
ix
i
n
ij i
() () () () ()() ()
,
++=
==
∑∑
11
.
Aax aa
ij
ij
n
ij ij
==
=
()
,1
- матрица квадратичной формы.
λ
λ
1
,...,
n
- n вещественных собственных значений матрицы A
n
+
- количество положительных собственных значений.
n
−
- количество отрицательных собственных значений.
n
0
- количество нулевых собственных значений с учетом кратности.
1.Если
n
+
= n или n
−
= n, то это эллиптическое уравнение.
UEx:U Уравнение Пуассона
∆∆uf
xx
n
=++,... где : =
22
∂
∂
∂
∂
1
22
.
2.Если
n
+
= n - 1, n
−
= 1, или n
+
= 1, n
−
= n - 1, то уравнение гиперболическое.
UEx:U uuf
tt
−=∆ - волновое уравнение.
Для уравнения Лапласа:
A
nn×
=
F
H
G
G
G
G
I
K
J
J
J
J
10 0
01
01
...
... ...
... ... ... ...
... ...
Для волнового уравнения:

www.uchites.ru
3
A
nn()()
...
... ...
... ... ... ...
... ...
+× +
=
−
−
F
H
G
G
G
G
I
K
J
J
J
J
11
10 0
01
01
3.Если
n
+
≠ 0, а 110
0
<
<
−=
−
nn n, а , то ультрагиперболическое уравнение.
UEx:U uu u u
xx x x xx x x
11 22 33 44
0+−−=.
4.Если
n
0
0≠ , то параболическое уравнение.
UEx:U uuf
t
−=∆ , и - уравнение теплопроводности.
A =
−
−
F
H
G
G
G
G
I
K
J
J
J
J
10 0
01
01
...
... ...
... ... ... ...
... ...
Определение.
Каноническим видом линейного дифференциального уравнения в частных производных
называется такой вид, когда матрица A является диагональной.
UПриведение к каноническому виду.
1) y=y(x), то:
u
u
y
y
x
u
u
yy
y
x
y
x
x
p
p
n
p
i
xx
pq
pq
n
p
i
q
j
i
ij
=⋅
=⋅⋅
=
=
∑
∑
∂
∂
∂
∂
∂
∂∂
∂
∂
∂
∂
1
2
1,
Уравнение (1) в новой системе координат:
∂
∂
∂
∂
∂
∂∂
y
x
a
y
x
u
yy
fy
p
i
ij
q
j
ij
n
pq
pq
n
,,
... ( )
==
∑∑
F
H
G
I
K
J
+=
1
2
1
(1')
Матрица Якоби:
I
y
x
p
i
pi
n
=
=
∂
∂
,1
.
В результате:
B
I
A
I
T
=
UEx:U
ufxy
A
xy
=
=
F
H
G
I
K
J
=⇒ =±
(,)
.
012
12 0
12
12
012
λ
λ
λ
гиперболическое уравнение.
1
2
1
2
uuf
xx yy
′′ ′′
−= - канонический вид волнового уравнения.
Замечание: тип уравнения может быть различный в различных точках.
www.uchites.ru
4
U§ 3.Постановка начальных и краевых задач для
уравнений в частных производных.
Задача Коши для волнового уравнения:
uufxttxR
uxxR
uxxR
tt
n
t
n
t
t
n
−= > ∈
=∈
=∈
R
S
|
T
|
=
=
∆ (,),( , )
(),
(),
0
0
0
ϕ
ψ
()
()
()
1
2
3
Уравнение теплопроводности
uuftx
tx Q
t
T
−=
∈
∆ (, )
(, )
()
()
4
5
Уравнение Пуассона
∆u
f
=
Определение.
Если малые изменения правой части уравнения приводят к большим изменениям в
решении, то задача считается некорректной.
∆u
f
x
Q=∈ (6)
uxQ
Q
∂
∂
=∈0 (7.1)
∂
∂
∂
∂
u
t
xQ
Q
=∈0 (7.2)
∂
∂
σ∂
∂
u
n
uxQ
Q
+
F
H
G
I
K
J
=∈0 (7.3)
(6)(7.1) - первая краевая задача, задача Дирихле.
(6)(7.2) - вторая краевая задача, задача Неймана.
(6)(7.3) - третья краевая задача.
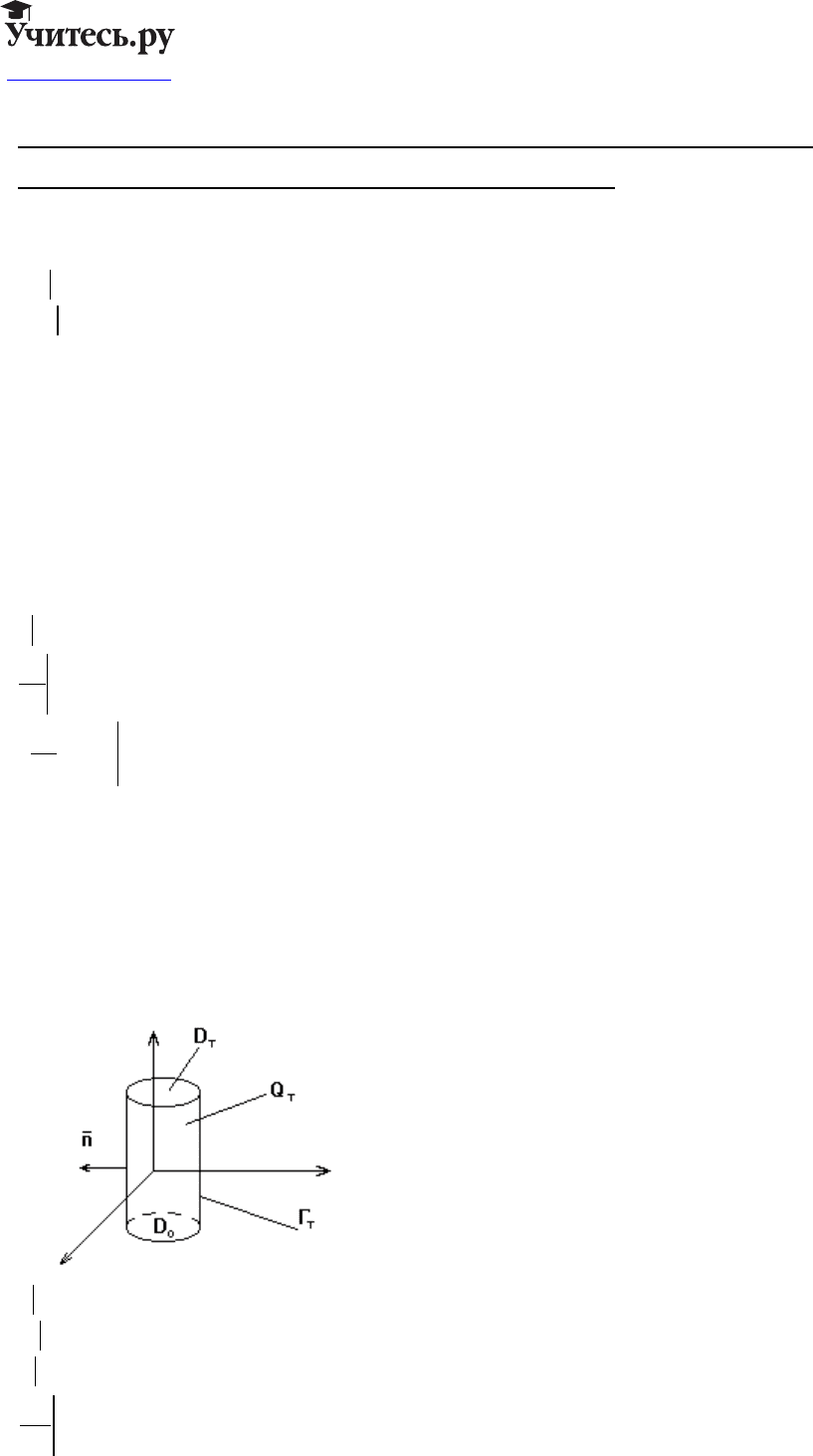
Волновое уравнение.
uuftx
tx Q
tt
T
−=
∈
∆ (, )
(, )
(8)
uxxD
t =
=
∈
0
0
ϕ
( ) (9)
uxxD
t
t
=
=
∈
0
0
ψ
( ) (10)
utx
T
T
Γ
Γ=
∈
0 ( , ) (11.1)
∂
∂
u
n
tx
T
T
Γ
Γ=∈0 ( , )
(11.2)

www.uchites.ru
5
∂
∂
σ
u
n
utx
T
T
+
F
H
G
I
K
J
=∈
Γ
Γ0 ( , ) (11.3)
(8) (9) (10) (11.1) - смешанные
(11.2) задачи
(11.3) (краевые задачи)
r
n - единичный вектор внешней нормали к поверхности.
На
D
0
задаются начальные условия.
На боковой поверхности - краевые задачи.
Параболическое уравнение.
uuftx txQ
tT
−= ∈∆ (, ), (, ) (12)
uxxD
t =
=
∈
0
0
ϕ
( ) (13)
utx
T
T
Γ
Γ=
∈
0 ( , ) (14.1)
∂
∂
u
n
tx
T
T
Γ
Γ=∈0 ( , )
(14.2)
∂
∂
σ
u
n
utx
T
T
+
F
H
G
I
K
J
=∈
Γ
Γ0 ( , ) (14.3)
(12) (13) (14.1) - первая, вторая и третья смешанные задачи
(14.2) для уравнения
(14.3) теплопроводности.
(14.1) - на границе задана температура;
(14.2) - задан тепловой поток;
(14.3) - задан теплообмен с окружающей средой.
U§ 4. Решение смешанных задач для волнового уравнения
методом Фурье (разделением переменных).
Первая смешанная задача.
uuftx txQ
tt T
−= ∈∆ (, ) (, ) (1)
uxxQ
t =
=
∈
0
ϕ
( ) (2)
uxxQ
t
t =
=
∈
0
ψ
( ) (3)
utx
T
T
Γ
Γ=
∈
0 ( , ) (4)
−= ∈∆vv
x
x
Q
λ
( ) (5)
v
Q
∂
= 0 (6)
Собственные значения (5) - (6) вещественны, имеют конечную кратность.
0
12
<<<<<
λ
λ
λ
... ...
s
λ
s
- изолир.
λ
s
s→∞ →∞, .
λ
λ
λ
12
12
, ,...,
, ,...,
s
s
vv v
- ортонормированный базис в LQ
2
().
В симметричной матрице собственные вектора, соответствующие разным собственным
значениям, попарно ортогональны.
Пусть функции
ϕ
ψ
xxftx
bg bg b g
,,, - разложены по базису vx
k
k
bg
mr
=
∞
1

www.uchites.ru
6
1
2
3
1
1
1
)() (); () () .
)() (); () () .
)(,) ()(); () (,)() .
ϕϕϕϕ
ψψψψ
xvx xvxdx
xvx xvxdx
ftx f tv x f t ftxv xdx
kk
k
kk
Q
kk
k
kk
Q
kk
k
kk
Q
==
==
==
=
∞
=
∞
=
∞
∑
z
∑
z
∑
z
тогда и u(t,x) можно разложить по базису
vx
k
k
bg
mr
=
∞
1
: ut x u tv x
kk
k
(, ) () ( )=
=
∞
∑
1
Почленно дифференцируем ряд 2 раза:
′′
+=
=
∞
=
∞
=
∞
∑∑ ∑
utvx ut vx ftvx
kk
k
kkk
k
kk
k
() ( ) () ( ) () ( )
11 1
λ
′′
+=
ut ut ft
k
k
k
k
() () ()
λ
(7)
Путём разложения решения в ряды по собственным функциям задачи алгебраизуем задачу,
получаем счётное число обыкновенных дифференциальных уравнений.
ux u vx
u
kk
k
kk
(, ) () ( )
()
00
0
1
=
=
R
S
|
T
|
=
∞
∑
ϕ
(8)
ux u vx
u
tkk
k
kk
(, ) () ( )
()
00
0
1
=
′
=
R
S
|
T
|
=
∞
∑
ψ
(9)
(7) (8) (9) - задача.
Решим однородное уравнение для (7):
µλ
µλ
λλ
2
0
1
+=
=±
=+−
л
k
kk kk k
i
ut a t b t
;
;
) ( ) cos sin
- общее решение однородного уравнения (7)
2) ( ) ( ) cos ( ) sin ;ut at t bt t
kk kk k
=+
λλ
′
+
′
=
′
+
′
=
R
S
|
T
|
atbt
at t t bt t t ft
kkkk
kk kkk kk
cos sin ;
( ) cos ( ) sin ( ).
λλ
λλ λλ
0
(10)
∆∆
∆
==−⋅
=⋅
=− ⋅
=⋅
z
z
λλ
λ
λ
λτ τ
τ
λ
λτ τ τ
kkk
kk
k
k
kk
t
k
k
kk
t
tf t
tf t
at f d
bt f d
: sin ( )
cos ( )
( ) sin ( )
( ) cos ( )
1
2
0
0
1
1

www.uchites.ru
7
В результате: ut t f d
kkk
t
( ) sin ( ) ( )=−⋅
z
λττ
τ
0
- частное решение неоднородного уравнения
(7).
ut a t b t t f d
kk kk k
k
kk
t
( ) cos sin sin ( ) ( )=++ −⋅
z
λλ
λ
λτττ
1
0
- общее решение уравнения
(7).
Подставим (8) и (9) в решение:
ua
ub
kkk
kkkk
()
() ,
0
0
==
′
==
ϕ
λψ
т.е.
b
k
k
k
=
ψ
λ
.
ut x t t t f d v x
kk
k
k
k
k
kk
t
k
k
( , ) cos sin sin ( ) ( ) ( )=++−⋅
R
S
|
T
|
U
V
|
W
|
z
∑
=
∞
ϕλ
ψ
λ
λ
λ
λτττ
1
0
1
Замечание: не обоснована сходимость рядов.
U§ 5.Решение смешанных задач уравнения
теплопроводности методом Фурье (разделения
переменных).
uuftx txQ
tT
−= ∈∆ (, ) (, ) (1)
uxxQ
t =
=∈
0
ϕ
() ( ) (2)
utx
T
T
Γ
Γ=∈0 ( , ) (3)
−= ∈∆vv
x
x
Q
λ
( ) (4)
v
Q
∂
= 0 (5)
λ
λ
1
1
,..., ,...
,..., ,...
s
s
vv
- собственные векторы и собственные значения.
ϕϕϕϕ
λ
() (); () () ;
(, ) () ( ); () (, ) ( ) ;
(, ) () ( );
() ( ) () ( ) () ( );
xvx xvxdx
ftx f tv x f t ftxv xdx
ut x u tv x
utvx utvx ftvx
kk
k
kk
Q
kk
k
kk
Q
kk
k
kk kkk kk
kkk
==
==
=
′
+=
=
∞
=
∞
=
∞
=
∞
=
∞
=
∞
∑
z
∑
z
∑
∑∑∑
1
1
1
111
′
+=ut ut ft
k
k
k
k
() () ()
λ
(6)
www.uchites.ru
8
u
uuv vx
kk
kkk
k
kk
k
()
() () () ( )
0
000
11
=
==
=
∞
=
∞
∑∑
ϕ
ϕ
ut Ce
k
k
t
k
()=
−
λ
- общее решение однородного уравнения (6)
ut C te
k
k
t
k
() ()=
−
λ
- частное решение неоднородного уравнения (6)
′
=
′
=
=
=
==
−
−
−−
=
∞
=
∞
z
z
∑∑
с te f t
с teft
с tefd
ut e f d
uuvxvx
k
t
k
k
t
k
k
t
k
t
k
t
k
t
kkk
k
kk
k
k
k
k
k
() ()
() ()
() ( )
() ( )
() () ( ) ( )
()
λ
λ
λ
λτ
ττ
ττ
ϕ
0
0
11
00
ut с eefd
kk
tt
k
t
kk
() ( )
()
=+
−−−
z
λλτ
ττ
0
- общее решение уравнения (6).
u с c
k
k
k
k
k
()0 == ⇒ =
ϕ
ϕ
ut x e e f d v x
k
tt
k
t
k
k
kk
(, ) ( ) ( )
()
=+
R
S
T
U
V
W
−−−
=
∞
z
∑
ϕττ
λλτ
0
1
Рассмотрим функцию:
ω
()
,;
,.
t
ce t
t
t
=
<
≥
R
S
|
T
|
−
−
1
1
2
1
01
ω
- бесконечно дифференцируема при t
<
1.
Если
t →1 из t <1, то:
−
−
→−∞
1
1
2
t
lim ( )
t
t
→
′
=
1
0
ω
, и при t
=
±1 функция склеивается как бесконечно гладкая.
ω
()t -финитная :
ω
∈
∞
&
()CR
www.uchites.ru
9
supp
ω
=−11, - замыкание множества, где
ω
отлична от 0.
ω
()tdt
−∞
∞
z
=1.
Введём
ωω
h
n
n
x
h
x
h
xRh() , ,=
F
H
G
I
K
J
∈>
1
0 - функция n переменных.
Свойства
ω
h
:
1)
ω
h
- бесконечно дифференцируемая, финитная:
ω
h
n
xCR()
&
()∈
∞
.
2)
sup ( )
ω
h
h
S= 0 - замкнутый шар радиуса h с центром в O.
ω
h
x()≥ 0.
3)
ω
h
R
xdx
n
() ,
z
=∀1 ( h > 0)
Доказательство.
ωωω
h
R
n
h
R
h
R
y
x
h
xdx
h
x
h
dx y dy
nn n
() ( )
z
z
z
=
F
H
G
I
K
J
==
=
1
1
, С находится из условия
ω
h
R
ydy
n
()
z
=1.
4)
Dx
C
h
C
h
n
α
α
α
α
ω
⋅≤ >
+
() , 0.
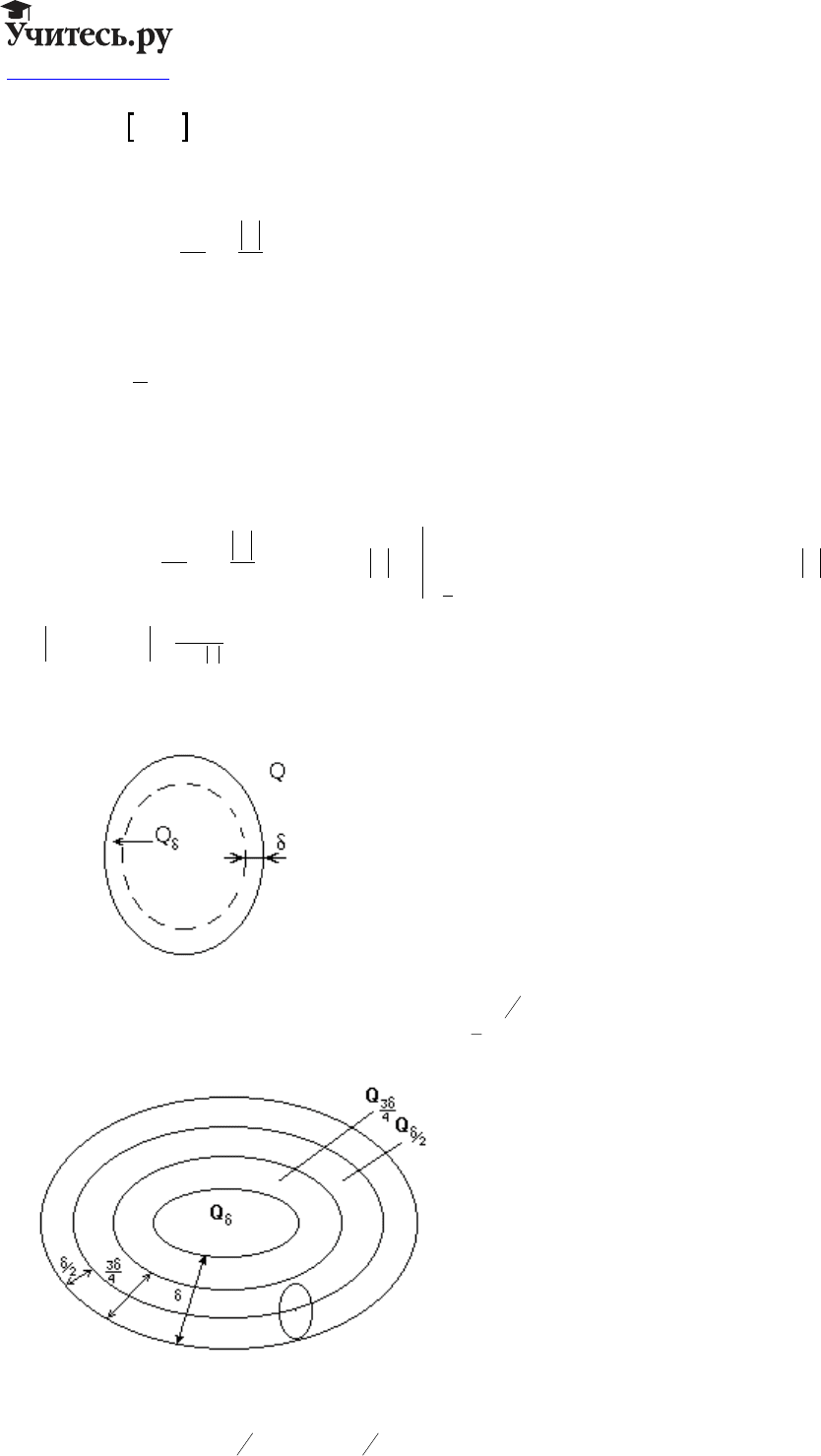
Обозначим:
QxQxQ
δ
ρ
∂
δ
=
∈
>>:(, ) 0
lq
ξω
δδ
δ
() ( )xxydy
Q
=−
z
4
3
4
Интеграл по x бесконечно дифференцируем.
Если
xQ∈
δ
, то: sup ( ) ( )
ω
δδ
44
xy S x−⊂

www.uchites.ru
10
Носитель функции принадлежит области интегрирования, и: xQ x
∈
⇒=
δδ
ξ
() 1.
Если
xQ∉
δ
2
, то
ξ
δ
()x = 0 : xQ x∈⇒
=
δδ
ξ
2
0 () .
Свойства функции
ξ
δ
()x :
1) ( )
&
();
ξ
δ
xCR
n
∈
∞
20 1)();≤≤
ξ
δ
x
31)() , ;
ξ
δδ
xxQ≡∈
40
2
)() , ;
ξ
δδ
xxQ≡∉
ξ
δ
()x - срезающая функция.
Пространство
L
2
.
Определение.
Пусть
QR
n
⊂ . Назовём множество функций ux x Q(),
lq
∈
, пространством LQ
2
(), если:
-
u
x
() - измеримы в Q;
-
∃
z
ux dx
Q
()
2
в смысле Лебега.
Вводится
(,) ( )( )
()
uv ux vxdx
LQ
Q
2
=
z
. Выполняются все аксиомы скалярного произведения.
Утверждение (без доказательства).
LQ
2
() - полное пространство.
Вводится
uuu
LQ
LQ
2
2
()
()
(,)= .
Свойства пространства
L
2
.
Теорема 1.
Множество финитных бесконечно дифференцируемых функций всюду плотно в
пространстве
LQ
2
() :
&
() ()
C
QLQ
∞
=
2
.
Доказательство.
Множество ступенчатых функций плотно в
LQ
2
().
Множество линейных комбинаций характеристических функций всюду плотно в
LQ
2
().
Доказать: любую характеристическую функцию измеримого множества можно сколь угодно
точно аппроксимировать финитными функциями.
Любое измеримое множество сколь угодно точно может быть аппроксимировано
открытыми областями.
Доказать: характеристическую функцию
χ
Ω
Ω
(),xQ
∈
можно сколь угодно точно
аппроксимировать финитными бесконечно гладкими функциями.
