Лекции - Уравнения в частных производных
Подождите немного. Документ загружается.

www.uchites.ru
21
∀∈ ∃ ∈fHQ FH
kk
() () Ω - продолжение f, такая, что:
1)
F
x
f
x
x
Q() () ( )=∈
2)
supp F ⊂Ω
3)
FCf
HHQ
kk
() ()Ω
≤ (5)
Замечание.
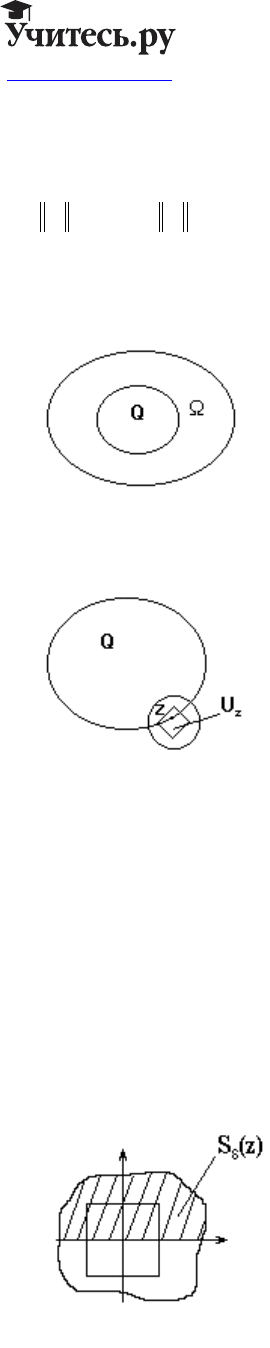
Лемма 1 - рассмотрены кубики, в теореме: из Q на
Ω
и все свойства, как в лемме 1.
Доказательство.
В окрестности каждой точки границы:
zQ
∈
∂
нарисуем шар Sz z
δ
δ
δ
() () , = .
Пусть в O(z) граница задаётся уравнением
xxzx
nn
=
′
=
′
ϕ
ϕ
(), () .
Введём новые переменные:
yxz
yxz
yx x
nnn
nn
111
111
=−
=−
=−
′
R
S
|
|
T
|
|
−−−
...
()
ϕ
- невырожденное преобразование координат.
Преобразование:
H
H
kk
→ - внутри пространства Соболева.
Во что перейдёт множество:
QSz∩
δ
()
Вырезали куб
K
a
.
Результат преобразования
Прообраз куба
K
a
- криволинейный кубик.
Покроем границу кубиками V
i
и выберем конечное подпокрытие.
(T
j
u)(y) = u(x(y)) (x
∈
V
j
) - переход от x к y,
переход от y к x :
T
y
j
−
→
1
: x
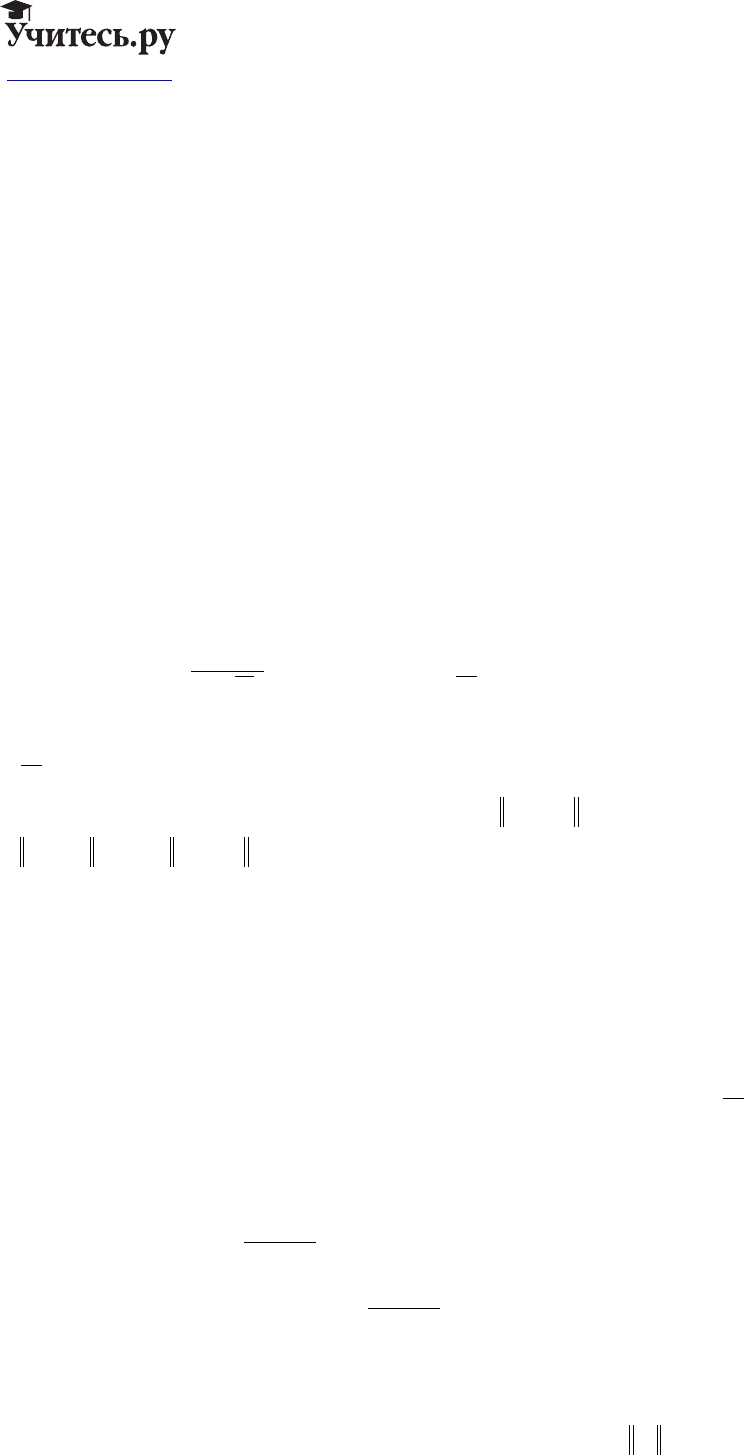
www.uchites.ru
22
supp
ϕ
jj
V⊂
Введём :
ψ
j
n
CR∈
∞
&
()
ψ
j
x()≡ 1 если x
j
∈
supp
ϕ
supp
ψ
jj
V⊂
ψ
j
на носителях
ϕ
j
обратятся в 1.
Fx T CT f
jj jj j
j
J
() ( )=
−
=
∑
ψϕ
1
1
Свойства оператора продолжения:
1. F(x) - ограниченный оператор;
2. Т.к.
ϕ
j
- финитная, то F(x) - финитная на Ω
Доказать: F(x)=f(x),если
xQ
j
∈ .
Fx f f f x
xQ
jj j
j
J
j
J
() ()
∈
==
===
∑∑
ψϕ ϕ
11
Замечание.
Теорема 1 остаётся справедливой для пространств
C
k
(следует из доказательства).
Теорема 2.
Пусть QR
n
⊂ - ограниченная область
∂
QC CQ HQ
kk
∈⇒
∞
=() () , CQ
∞
()- всюду плотно в HQ
k
().
Доказательство.
Рассмотрим произвольную функцию
∀
∈
fHQ
k
().
Q ⊂Ω - ограниченная.
F-продолжение f. Так как F - финитная в Ω, то
FF h
h
H
k
−
→→
()
,
Ω
00
fF FF
h
HQ
h
H
kk
−≤−→
() ()Ω
0
Сепарабельность пространств Соболева.
Теорема.
Пусть
QR
n
⊂ - ограниченная область,
∂
QC
k
∈
, тогда :
HQ
k
() - сепарабельное.
Построениe счётного всюду плотного множества.
Доказательство.
Рассмотрим
f
HQ
k
∈ () ; продолжение функции f :
∃
∈
⊂FH K Q K
k
()
π
π : .
Аппроксимируем функцию F . Множество финитных, бесконечно дифференцируемых
функций (в силу свойств осреднений) всюду плотно в пространстве финитных функций
FHK
k
∈ ()
π
.
Очевидно :
FF
e
mm m
m
imx
n
k
m
==
∑
(,)
/
()
; ,...,
2
2
1
π
.
Где коэффициенты :
FFx
e
dx
m
imx
n
K
=
−
z
()
()
(,)
/
2
2
π
π
.
Пусть H - сепарабельное гильбертово пространство.
Определение.
Функции
{}e
i
образуют ортонормированную систему, если e
i
=
1 , и (, )ee i j
ij
=
≠
0 , .
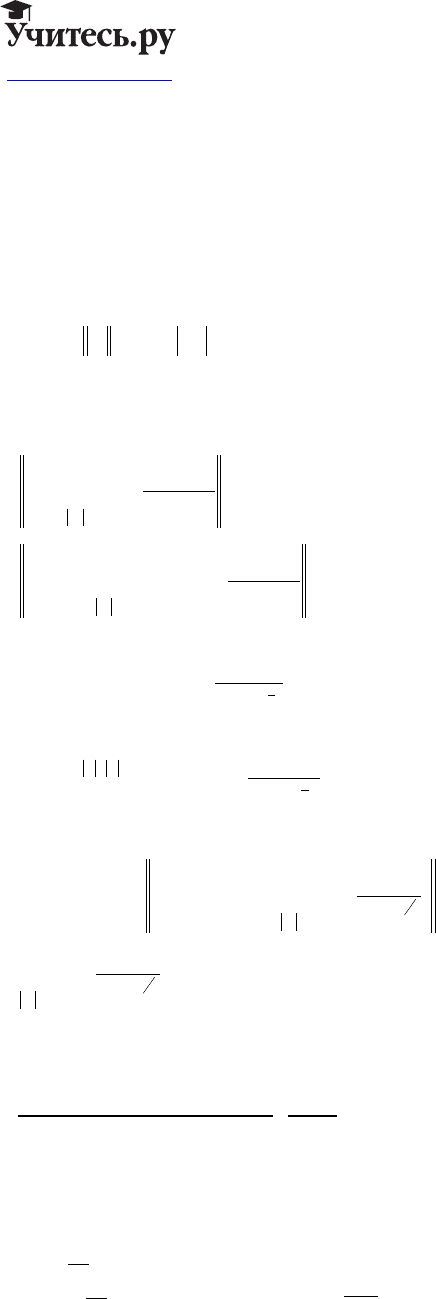
www.uchites.ru
23
Утверждение.
В каждом сепарабельном гильбертовом пространстве существует ортонормированный базис,
т.е. такая система
{}e
i
,что ∀∈ =
=
∞
∑
xH x xe
ii
i
,
1
.
Разложение по этому базису единственно, и :
xxe
ii
=
(, ).
Равенство Парсеваля.
xx
i
i
22
1
=
=
∞
∑
.
Пространство
L
2
- сепарабельное гильбертово пространство с ортонормированным базисом :
можно взять систему экспонент (нормированную).
Разложение в сходящийся ряд :
FF
e
N
Df DF
e
N
m
imx
n
mN
LK
m
imx
n
mN
LK
−→→∞
−→→∞
≤
≤
∑
∑
(,)
/
()
(,)
/
()
()
,
()
()
,
2
0
2
0
2
2
2
2
π
π
π
αα
π
Определим вид коэффициентов Фурье:
()
()
(,)
DF DF
e
dx
m
imx
K
n
αα
π
π
==
−
z
2
2
проинтегрируем по частям и получим :
=− ⋅ ⋅ = ⋅
+
−
z
() ( )
()
()
(,)
1
2
2
αα
α
π
α
π
im F
e
dx i m F
imx
K
m
n
, где
() ( )( )...( )im im im im
n
n
⋅=⋅ ⋅⋅ ⋅⋅⋅
α
αα α
12
12
di
Получаем :
DF D F
e
m
imx
mN
LK
n
αα
π
π
−⋅ →
≤
∑
(
()
),
(,)
()
2
0
2
2
и следовательно :
F
e
Fx H K
m
imx
mN
k
n
(,)
()
() ( )
2
2
π
π
≤
∑
→ в
F можно точно аппроксимировать линейными комбинациями экспонент.
Искомое множество - линейное пространство экспонент с рациональными коэффициентами.
UСлед функции из HU
kU
(Q).
Для функции из
LQ
2
() понятие значения на (n-1)- мерной поверхности не определено.
Если
f
LQ∈
2
() удовлетворяет условиям дифференцируемости, то :
определение следа функции на (n-1)- мерной поверхности.
Рассмотрим
QR
n
⊂ -ограниченную область,
∂
QC
∈
1
.
SQ⊂ - (n-1) - мерная поверхность,
S
C
∈
1
.
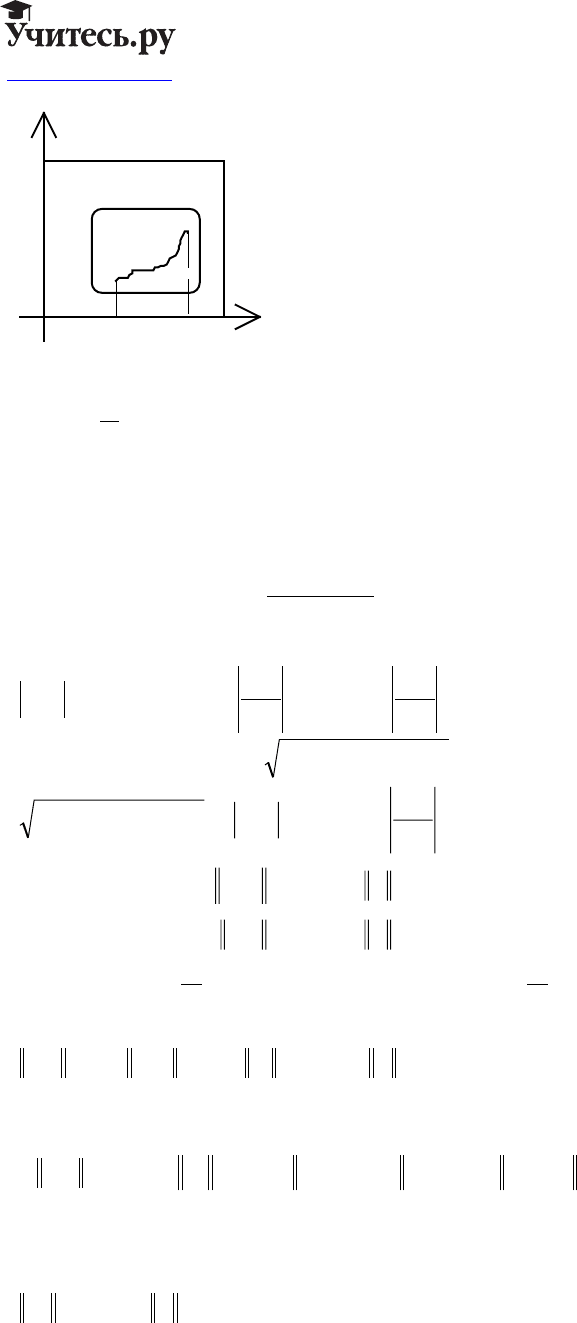
Пусть
QK xai n
i
⊂=<< ={,,}01
www.uchites.ru
24
S
K
a
a
Q
D
Можно разбить на конечное число простых кусков, однозначно проецирующихся на
координа тные плоскости и описывающиеся уравнением :
Sx x
n1
=
′
ϕ()
ϕ∈ ∈CD f CQ
11
(),
&
()
Для любой непрерывной функции след - её значение на поверхности, однозначно
продолженое по непрерывности.
f
fx x x D
S
| ( , ( )),
1
=
′′ ′
∈ϕ где
Так как f=0 вне области Q , то по формуле Ньютона-Лейбница :
f
fx x
fx
d
S
n
n
x
n
|(,())
(,)
()
1
0
=
′′
=
′
′
z
ϕ
∂ξ
∂ξ
ξ
ϕ
Оценим :
fd
f
da
f
dxa
S
x
n
n
x
n
n
a
n
|,()
() ()
1
2
2
00
2
0
2
1≤⋅⋅ ≤⋅
′
<
′′
z
z
z
ϕϕ
ξ
∂
∂ξ
ξ
∂
∂ξ
ξϕ
Обе части умножим на
1
11
22
+++
−
ϕϕ
xx
n
... и проинтегрируем по D :
1
111
1
1
21
1
21
1
22
2
1
2
2
3
+++ ⋅ ≤⋅
′
≤
≤
−
z
z
ϕϕ
∂
∂ξ
ξ
xxS
S
n
K
n
S
LS
HQ
S
LS H Q
n
fdsC
f
dx d
fCf
fCf
... |
|
|
()
()
() ()
f- финитная.
Так как
f
CQ∈
1
() может быть продолжена в Ω ()Q ⊂
Ω
финитным образом,
FC∈
&
()
1
Ω , причём
f
F
SS
||=
fFFCf
SLS S
LS H H Q
||
()
() () ()
2
2
11
=
≤
≤
Ω
f
HQ∈
1
()
Существует последовательность
{} () {} ()ffHQ fCQ
pp pp=
∞
=
∞
→∈
1
1
1
1
в , где :
fCf ff Cff
S
LS
p
HQ
pS qS
LS
pq
HQ
|,||
()
() () ()
2
1
2
1
33
0≤−≤−→
Отсюда следует фундаментальность последовательности следов в
LS
2
()
LS
2
()- полное, следовательно{|}f
pS
- сходится,
f
fLS
pS
LS
S
|()
()
2
2
⎯→⎯⎯∈
Перейдём к пределу, получим :
fCf
S
LS H Q
2
1
3
() ()
≤
Утверждение.
Определение
f
S
не зависит от выбора аппроксимирующей последовательности {}f
p
.
Доказательство.
Пусть есть две последовательности
f
ff
pp
,
%
→ в HQ
1
().
www.uchites.ru
25
Пусть
f
ff f LS
pS S pS S
|
%
|
%
()→→ , в
2
.
Следовательно, должны совпадать два предела в
LS
2
().
Рассмотрим
ff ff f f f f
Cff f f f f p
SS
LS
SpS
LS
pS pS
LS
pS S
p
HQ
pp
HQ
p
−≤− +− +−≤
≤ − ++ +−→ →∞
%
||
%
||
%
%%
,.
()
()
()
()
()
2
2
2
1
1
3
0
ej
Значит :
ff p
SS
LS
−→→∞
%
,
()
2
0
, и
f
f
SS
=
%
.
Если функция непрерывна в
Q и принадлежит HQ
1
(), то её понятие следа как значения
непрерывной функции и как предела совпадают.
UФормула интегрирования по частям.
Пусть Q- ограниченная,
∂QC fgHQ∈
∈
11
,, () .
f g dx f g n x ds f g dx
x
Q
QQ i x
QQ
i
⋅= ⋅ ⋅ −⋅
z
z
z
| | cos( , )
∂∂
∂
, n - единичный вектор внешней нормали к
∂
Q .
UТеорема Реллиха-Гординга.U
Если
f
H
∈
2
, то
f
H
∈
1
, если f
p
n
s
сходится в
H
2
, то f
p
n
s
сходится в
H
1
.
Пространство Соболева с большим показателем дифференцируемости k компактно вложено
в ространство Соболева с меньшим показателем.
Пусть
QR
n
⊂ - ограничена, ∂QC∈
1
, тогда : HQ
1
() - компактно вложено в LQ
2
().
Множества, ограниченные в
H
1
, являются предкомпактными в L
2
.
Определение.
Предкомпактными называются такие множества, замыкания которых компактны.
Из любой ограниченной последовательности функций из
HQ
1
bg
можно выбрать
подпоследовательность, сходящуюся в
LQ
2
().
Или : Для
∀
≤
V
n
HQ
1
1
()
можно выбрать {}V
n
, сходящуюся в LQ
2
().
Доказательство.
1. Продолжим функции
V
n
финитным образом в более широкую область Ω, Q ⊂Ω.
V
HV
nn
∈⊂
1
(),ΩΩ supp .
Оператор продолжения ограничен, и :
VC
n
H
1
()Ω
≤
.
Т. к. множество финитных, бесконечно дифференцируемых функций всюду плотно в
пространстве функций
H
1
с компактными носителями, то без ограничения общности
рассуждений можно считать, что все функции
V
CR
n
n
∈
∞
&
() - бесконечно дифференцируемы
в
R
n
.
V
n
n
lq
=
∞
1
- из неё будем выбирать сходящуюся подпоследовательность.
Используем преобразование Фурье :
%
() ( ) ( )
(, )
V
Vxe dx
nn
ix
R
n
n
ξπ
ξ
=
−
−
z
2
2
.
( , ) ...ξξξ ξxxx x
nn
=+++
11 22
.
В силу финитности :
%
() ( ) ( ) ,( )
(, ) (, )
()
V
Vxe dx V e
nn
ix
R
n
ix
L
n
n
n
ξπ π
ξξ
==
−
−
−
−
z
22
22
2
e
j
Ω
www.uchites.ru
26
Оценим по неравенству Коши-Буняковского:
%
() () ()
()
(, )
V V e dx C mes C
nn
L
n
ix
n
ξπ π
ξ
2
2
2
1
2
22≤⋅ ≤⋅ =
−−
z
Ω
Ω
Ω
Свойство.
В гильбертовом пространстве из ограниченной последовательности можно выделить слабо
сходящуюся подпоследовательность.
V
n
k
- слабо сходящаяся в L
2
()Ω .
(,)
()
V
nL
k
ϕ
2
Ω
- сходящаяся для любой непрерывной линейной функции ϕ∈L
2
()Ω .
В качестве
ϕ
возьмём функции :
ϕπ ξ
ξ
=
−
() ()
(, )
2
2
n
k
eV
ix
n
, и - сходится
∀
∈
ξ
R
n
Докажем, что
V
x
n
k
() - фундаментальна в L
2
()
Ω
VV VV V V d
nn
LR
nn
LR
nn
R
km
n
kk
n
km
n
−=−=− =
z
22
22 2
() ()
%%
()
%
()ξξξ
=− +−
<<
zz
%%
VVd VVd
nn
R
I
nn
R
I
km km
2
12
ξξ
ξξ
1244 344 1 244 344
R
| |<Rξ
Так как последовательность
{
%
()}V
n
k
ξ сходится для любых ξ и ограничена, то для интеграла
I
1
применяем теорему Лебега о предельном переходе под знаком интеграла, получаем :
I
1
→→
∞
∀0 при km
R
,,, где
R
- радиус шара.
I
R
VVd
R
VVd
Rx
VV dx
C
R
nn
R
nn
R
nn
R
j
n
km km
n
km
n
2
2
2
2
2
2
2
2
2
2
2
1
1
≤−≤−= −≤
<
=
z
z
z
∑
ξ
ξ
ξ
ξ
∂
∂
ξ
di
исходя из теоремы Планшереля (в обратную сторону) и свойств преобразования Фурье :
V
xV
V
iV
ViV
Xj
X
LR
j
LR
n
j
j
n
n
()
%
()
%
()
%
...
()
()
↔
↔⋅ ⋅
=⋅⋅
=+++
ξ
ξξ
ξ
ξξξ ξ
2
2
2
2
1
2
2
22
Выбором R, интеграл
I
2
можносделать сколь угодно малым, т.е. :IR
2
0→→∞, .
Если
R
→∞ и k,m - выбрать , то : VV
nn
L
km
−→
2
2
0
()Ω
, и последовательность
V
n
k
n
s
- фундаментальна.
UФормула интегрирования по частям
www.uchites.ru
27
f gdx f g n x ds f g dx
xQQix
QQQ
i
=⋅⋅ −⋅
z
z
z
| | cos( , )
∂∂
∂
(1)
∀∈ ⊂fg H Q Q R
n
,()
1
- ограничена,
∂
QC
∈
1
.
f g dx f g n x ds f g dx
mx m
Q
mQ
Q
mQ i m mx
Q
i i
⋅= ⋅⋅ −⋅
z
z
z
| | cos( , )
∂
∂
∂
(2)
f
gCQ
ff
gg m
ff gg m
mm
m
HQ
m
HQ
mQ Q
LQ
mQ Q
LQ
,()
,
|| , || ,
()
()
() ()
∈
−→
−→ →∞
−→ −→→∞
1
1
1
22
0
0
00
∂∂
∂
∂∂
∂
В уравнении (2) перейдем к пределу при
n →
∞
, получаем уравнение (1).
UПространство
&
()HQ
1
U
Определение.
Назовём пространством
HQ
1
o
() замыкание пространства финитных непрерывно
дифференцируемых функций в
HQ
1
().
HQ
1
o
()- замыкание
&
()
C
Q
1
в HQ
1
().
Если есть
uCQ uu m
mm
HQ
∈−→→
∞
&
(): ,
()
1
1
0 , то :
uuu Cuu m
Q
LQ
QmQ
LQ
m
HQ
||| ,
() ()
()
∂∂∂
22
1
0=− ≤− → →∞.
Если
uHQ∈
1
o
(), то u
Q
|
∂
= 0. Справедливо и обратное утверждение.
Теорема.
HQ uHQ u
Q
11
0
o
() (): |=∈ =
∂
ns
.QR
n
⊂ - ограничена,
∂
QC
∈
1
.
Определение.
Эквивалентные нормы.
Пусть H - гильбертово пространство со скалярным произведением ( . , . ).
Скалярное произведение
( . , .
′
)
называется эквивалентным ( . , . ) , если :
∀∈ ≤
′
≤xH Cxx xx Cxx, (,) (,) (,)
12
xxxx xx=
′
=
′
(,), (,).
Из эквивалентности скалярных произведений можно пользоваться любым.
Теорема 2.
В пространстве
HQ
1
o
() можно ввести скалярное произведение по формуле :
(,)
()
uv u vdx
HQ
Q
′
=∇∇
z
1
o
(3)
Доказательство.
(,)
(,) (,)
()
()
&
()
u v u vdx uvdx
uu uu
HQ
QQ
HQ
HQ
1
1
1
o
o
=∇∇ +
′
≤
z
z
Надо доказать :

www.uchites.ru
28
(,) (,)
() ()
uu C uu
HQ HQ
′
≥
11
1
oo
(4)
Доказательство от противного.
∀> ∃ ∈
′
<NuHQuu
N
uu
N
HQ HQ
0
1
1
2
11
o
oo
():(,) (,)
() ()
u
N
u
N
HQ
N
HQ
11
1
oo
() ()
≤
Будем считать, что
u
N
HQ
1
1
o
()
= , а это значит : u
N
uN
N
HQ
N
x
i
1
1
0
o
()
,<⇒ → →∞
uu LQ
N
k
→ в
2
() (по теореме Реллиха-Гординга)
() (),
(), (),
()
uLQN
uu HQuHQu
Nx
N
HQ
ki
k
→→
∞
→∈=
0
1
2
11
1
в
в
oo
o
u i N u const
x
i
== ⇒=01, ( ,..., )
Имеем противоречие. Теорема доказана.
UОбобщенное решение задачи Дирихле для уравнения Пуассона
−= ∈
=
R
S
T
∆ux f x x Q
u
Q
() () ( )
|
- уравнение Пуассона (1)
- условие Дирихле (2)
∂
0
Пусть
uCQ∈
2
()- решение задачи (1)-(2). Возьмем
v
CQ
∈
&
()
1
и умножим (1) на
v
,
проинтегрируем и получим :
−∇ =
z
z
u v dx f v dx
QQ
. Если
v
- гладкая, то :
∇∇ =
z
z
u v dx f v dx
QQ
(3)
Определение.
Функция
uHQ∈
1
o
() называется обобщенным решением задачи (1)-(2), если для любой
функции
v
HQ∈
&
()
1
выполняется тождество (3).
При исследовании обобщенных решений
f
LQ
∈
2
().
Лемма.
Существует линейный ограниченный оператор
ALQ HQ:() ()
2
1
→
o
, такой, что
(,) ( ,) ( ( ), ( ))
()
()
u v Au v v H Q u L Q
LQ
HQ
2
1
1
2
=
′
∀∈ ∈
o
o
.
При этом
AHQ HQ:() ()
11
oo
→ -компактный самосопряжённый положительный оператор.
По определению :
f
vuv
uLQ
() (,)
()
=
2
.
f
- антилинейный по
v
.
fv u v Cu v
u
LQ LQ LQ H Q
()
() () () ()
/
≤⋅≤ ⋅
22 2
1
1
o
.
f -ограничен, следовательно применим теорему Рисса :
(,) ( ,)
()
()
/
uv F v
LQ u
HQ
2
1
=
o
F - линейно зависит от u.
FCu
u
HQ LQ
1
2
1
o
()
/
()
≤
FAu
u
= .
Компактность очевидна по теореме Реллиха-Гординга.
www.uchites.ru
29
(,) (,) (,) (,) (, )
()
/
()
() ()
()
/
Au v u v v u Av u u Av
HQ
LQ
LQ HQ
HQ
1
2
2
1
1
o
o
o
===
′
=
Самосопряженность доказана.
(,) (,) ,
()
/
()
Au u u u u
HQ
LQ
1
2
00
o
=>≠
Теорема.
Для любой функции
f
LQ∈
2
() cуществует единственный uHQ∈
1
o
() краевой задачи (1) (2).
При этом
uCf
HQ LQ
1
2
o
() ()
≤ (4)
Задача Дирихле для уравнения Пуассона корректна, т.е. существует единственное решение
непрерывно зависящее от правой части.
Доказательство.
∇⋅∇ = ⋅
=∀∈
=≤
z
z
u v dx f v dx
uv Af v v H Q
uAfCf
QQ
HQ HQ
HQ HQ LQ
(,) ( ,) ( )
()
/
()
/
() () ()
11
11
2
1
oo
oo
o
UСобственные значения и собственные функции оператора Лапласа.
−= ∈
=
R
S
T
∆ux ux x Q
u
Q
() () ( )
|
λ
∂
(1)
(2)0
Определение.
Функция
uHQ∈
1
o
() называется обобщенной собственной функцией оператора -∆ с
условиями Дирихле, соответствующей обобщенному собственному значению λ, если она
удовлетворяет следующему интегральному тождеству :
∇∇ = ∀∈
z
z
u v dx uvdx v H Q
QQ
λ ,()
1
o
(3)
Теорема.
1. Собственные значения задачи (1) (2), являются вещественными, положительными,
изолированными, имеют конечную кратность, и :
λ
s
s→+∞ →+∞,
2.Существует ортонормированный базис в
LQ
2
() состоящий из собственных функций
задачи (1) (2)
{}u
s
.
3.
u
S
S
λ
R
S
|
T
|
U
V
|
W
|
составляет ортонормированный базис в HQ
1
o
bg
с эквивалентным скалярным
произведением :
(,)
()
/
uv u vdx
HQ
Q
1
o
=∇⋅∇
z
(4)
Доказательство.
Интегральное тождество (3) можно записать в виде :
(,) ( ,)
()
/
()
/
u v Au v
HQ HQ
11
oo
=λ , uAu Auu=⇒
=
λ
µ
,
µµµ
µ
123
00≥≥≥> → →
∞
... ,
s
s при .
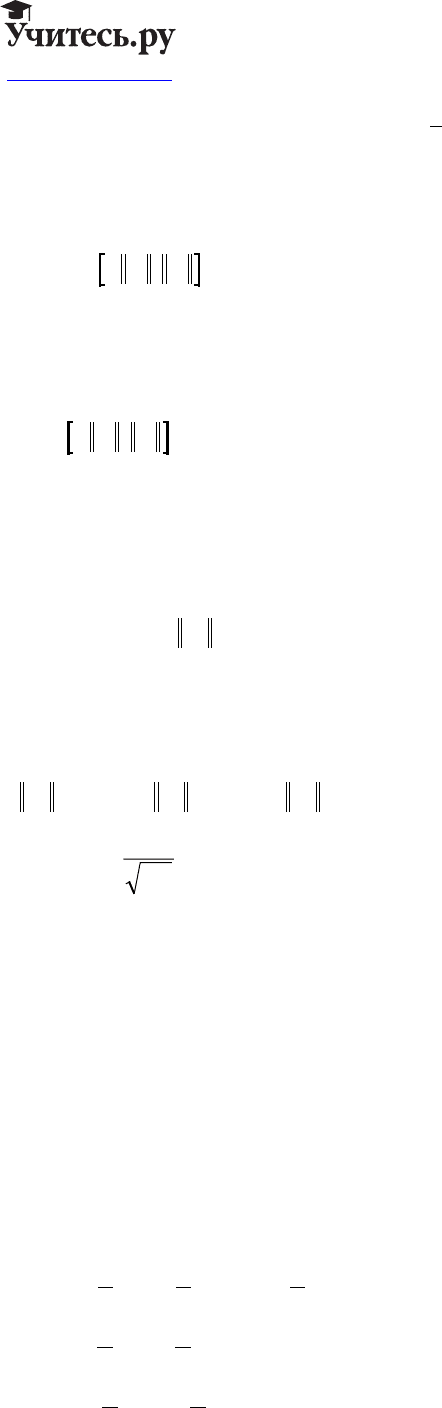
www.uchites.ru
30
Эквивалентная задача : Au u=
<
µ
µ
λ
,( )
1
Теорема 1.
Если
A
H
H
: → - линейный ограниченный самосопряженный оператор, тогда спектр
σ()A - вещественный, и :
σ() ,AAA⊂−
Теорема 2.
Пусть
A
H
H
: → - компактный, самосопряженный оператор, тогда σ()A состоит из {0} и
некоторого (конечного или счетного) множества изолированных собственных значений
конечной кратности :
λ
s
AA∈− ,
{0} всегда принадлежит спектру компактного оператора.
Теорема 3.
Пусть
A
H
H
: → - копактный, самосопряженный оператор, тогда существует
ортонормированный базис в пространстве
H
, состоящий из собственных функций этого
оператора :
∃⊂{}uH
s
.
Для удобства
u
s
LQ
2
1
()
= ,
(,) (,)
()
/
()
uu uu
sr
HQ
ssrLQ
1
2
o
=λ .
Значит : {}u
s
- ортонормированная система в LQ
2
().
Так как
HQ
1
o
() всюду плотно в LQ
2
(), то {}u
s
образует ортонормированный базис в LQ
2
().
uuu
s
HQ
ss
LQ
s
1
2
22
1
o
() ()
,==λ
Значит :
u
S
S
λ
R
S
|
T
|
U
V
|
W
|
образует ортонормированный базис в HQ
1
o
().
Рассмотрим задачу :
−+ = ∈∆uAu fx xQ
1
() ( ) (1)
где
Au a x u a x u x
ix
i
n
i
10
1
=+
=
∑
() ()()
Краевые условия :
u
Q
|
∂
= 0 (2)
−+ =∆vAv
1
0 (3)
v
Q
|
∂
= 0 (4)
Aw a xwx a xwx
T
ix
i
n
i
10
1
=− +
=
∑
( ()()) ()()
−+ =wAw
T
1
0 (5)
w
Q
|
∂
= 0 (6)
()∇∇+ =
z
z
uAudxfdx
QQ
ϕϕ ϕ
1
(7)
()∇∇+ =
z
vAvdx
Q
ϕϕ
1
0 (8)
()∇∇+ =
z
wAwdx
T
Q
ϕϕ
1
0 (9)
