Лекции - Уравнения в частных производных
Подождите немного. Документ загружается.


www.uchites.ru
71
lim lim ( , ) ( , )
lim lim ( , ) ( , )
,,
,,
ε
ε
τ
ε
ε
ξτ
ξτ
→→∞
→→∞
=−−
=−
zz
z
0
0
0
0
2
0
N
N
R
N
N
R
I dt U x t Lu x t dx
IUxuxdx
n
n
Т.к.
ξ
N
xN() ,→→∞1 , то
Uxux dx
R
n
(,)(,)
ξε τε
−−=
z
произведём замену
x
−
=
ξ
ε
η
2
, тогда x =+
ξεη
2
=+−=
−
z
1
2
2
()
(,)(,)
π
εη τ ε η ξ τ
η
n
R
eUx d u
n
lim lim ( , )
,,
ε
ε
ξ
τ
→→∞
=
0
1
N
N
Iu.
Если докажем, что остальные пределы дают 0.
Формула Пуассона:
u dt U x t Lu x t dx U x u x dx
RR
nn
(,) ( , ) (,) ( ,)(,)
ξτ ξτ ξτ
τ
=−− +−
z
z
z
0
0
uxt d Ux t Lu d Ux tu d
t
RR
nn
(,) ( , ) (,) ( ,)(,)=−− +−
z
z
z
τξτξτξ ξξξ
0
0
Можно найти решение задачи Коши для уравнения теплопроводности:
Рассматривается задача:
Lu x t u u f x t t T
t
(,) (,) ( )=− = <<∆ 0 (1)
ux x x R
n
(,) () ( )0 =∈
ϕ
(2)
Если решение из рассматриваемого класса существует, то оно представляется формулой:
uxt d U x t f d U x t d
t
RR
nn
(,) ( , ) (,) ( ,)()=−− +−
z
z
z
τξτξτξ ξϕξ
ξ
0
.
В рассматриваемом классе решений задача Коши для уравнения теплопроводности может
иметь не более 1 решения.
IdtUxtxuxtdx
NN
xN
3
1
,,
(,)()(,)
ε
ε
τ
ε
ξτ ξ
=−−
−
<+
zz
∆
IdtUxtxuxtdx
NN
xN
4
1
,,
(,)()(,)
ε
ε
τ
ε
ξτ ξ
=−−
−
<+
zz
∆
NxN<<+1
Применим теорему Лебега о предельном переходе под знаком интеграла
(необходимо, чтобы все элементы последовательности были ограничены интегральной
функцией).
U x t u x t dx C U x t dx C
RR
nn
(,)(,) (,)
ξτ ξτ
−−⋅ ≤ −− =
zz
00
где :
ε
τ
ε
<<−t .
Подынтегральная функция ограничена .
Так как :
Uxt
t
e
n
x
t
(,)
()
()
ξτ
πτ
ξ
τ
−−=
−
−
−
−
1
2
2
4
ej
, то :
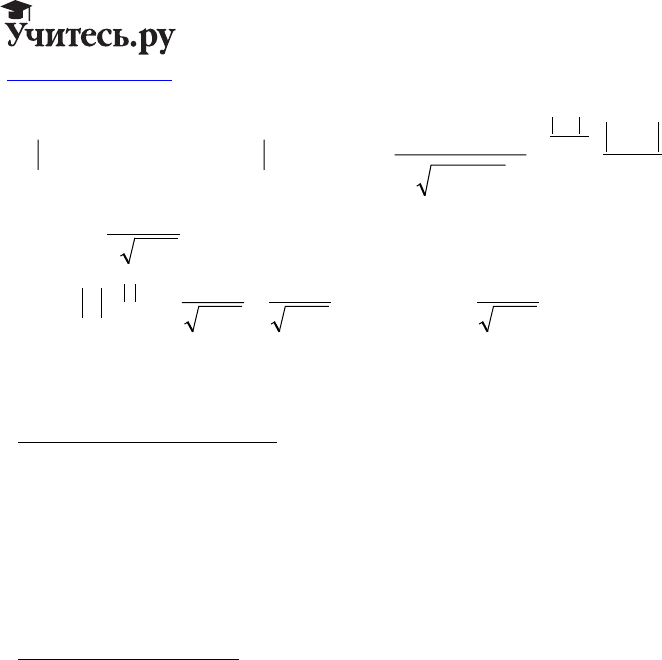
www.uchites.ru
72
∇−−⋅ ≤⋅
−
⋅
−
−
≤
zz
−
−
−
UxtuxtdxCC
t
e
x
t
dx
R
n
x
t
R
n n
(,)(,)
()
()
ξτ
πτ
ξ
τ
ξ
τ
01
4
1
2
2
ej
Замена :
x
t
−
−
=
ξ
τ
η
2
.
≤⋅
−
≤
−
−
z
Ced
t
C
t
R
n
2
3
2
1
ηη
ττ
η
, а интеграл
dt
t
t
τ
−
z
0
- сходящийся.
Сделано ограничение интегрируемой функцией.
Можно применять теорему Лебега о предельном переходе.
UТеория Фредгольма
(в Гильбертовом или Банаховом пространстве).
Рассмотрим компактный оператор
A
H
H
H
:,→
−
гильбертово пространство.
Изучаем уравнение :
()
E
Au
f
−
=
(1)
однородное уравнение
()
E
Av
−
=
0 (2)
однородное сопряженное уравнение
()EAw
−
=
∗
0 (3)
UТеорема Фредгольма.U
Теорема.
1. Если однородное уравнение (2) имеет единственное тривиальное решение, то
неоднородное уравнение (1) имеет единственное решение для любой правой части из
гильбертова пространства H.
2. Если уравнение (2) имеет нетривиальное решение, то тогда неоднородное уравнение (1)
разрешимо тогда и только тогда, когда правая часть уравнения (1) ортогональна всем
решениям уравнения (3) :
(, )fw
H
=
0.
3. Размерность ядра оператора
E
A− равна размерности оператора
E
A−
∗
и конечна.
dim ( ) dim ( )NE A NE A−= − <∞
∗
.
Введём :
T
E
A=−, тогда
T
E
A
∗
∗
=−.
Лемма 1.
di
m
()
N
E
A−<∞, dim ( )NE A−
<
∞
∗
.
Доказательство.
Предположим противное :
di
m
()
N
E
A
−
=
∞
.
Ядро - замыкает линейное подпространство.
x
N
E
A
x
Ax
x
Ax∈−⇔−=
=
() ,0
Следовательно единичный шар отображается на себя (в некомпактное множество), а
оператор компактный.
Ядро - замыкание бесконечномерного подпространства Гильбертова пространства.
Имеем противоречие, доказывающее теорему.
Лемма 2.
ℜ−()
E
A , ℜ−
∗
()EA - замкнуты в подпространстве.
Доказательство.
Пусть
yEAyy
nn
∈ℜ − →(), . Докажем, что y
E
A
∈
ℜ
−
().
∃=−xy EAx
nn n
:().
Разложим
x
n
на ортогональные составляющие.
xxx
nnn
=
′
+
′′
, где
′
∈−
′′
∈
−
⊥
x NEA x NEA
nn
(), ().
Значит :
yEAx
nn
=−
′
() .
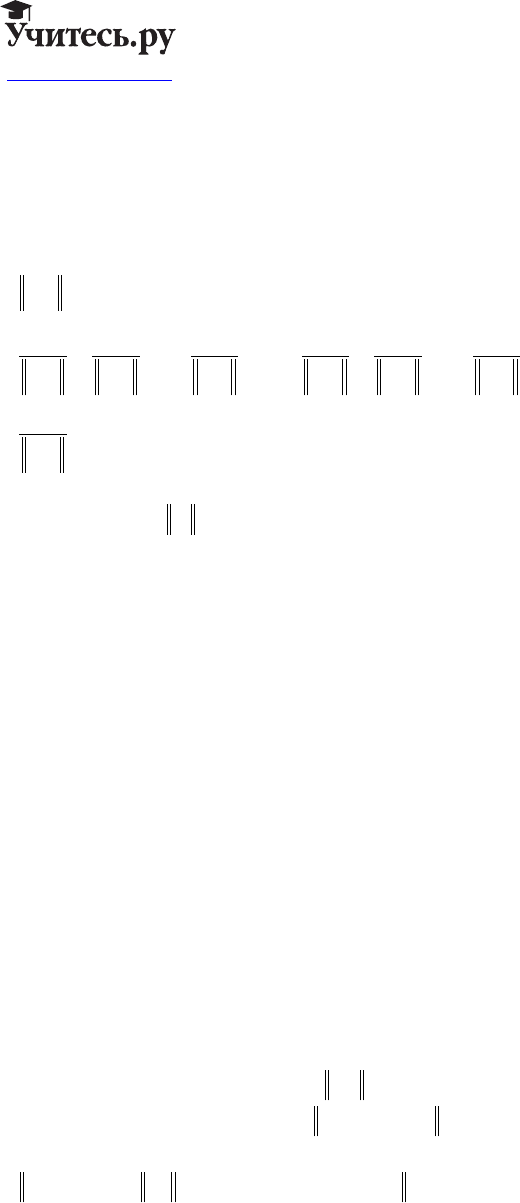
www.uchites.ru
73
1). {}
′
x
n
- ограниченная последовательность, следовательно можно выбрать
подпоследовательность
′
x
n
k
такую, что Ax
n
k
′
- сходящаяся.
Тогда :
yxAx
nn n
kk k
=
′
−
′
′
. В этом случае
′
x
n
k
сходится в H.
′
→=−⇒∈ℜ
−
x x y x Ax y E A
n
k
000
,().
2).
{}
′
x
n
- неограниченная. Можно выбрать подпоследовательность {}v
n
такую, что:
′
→∞x
n
k
, тогда :
y
x
x
x
A
x
x
n
n
n
n
n
n
k
k
k
k
k
k
′
=
′
′
−
′
′
F
H
G
G
I
K
J
J
,
%
%
%
%
%
%
y
x
x
x
A
x
x
n
n
n
n
n
n
k
k
k
k
k
k
′
=
′
′
−
′
′
F
H
G
G
I
K
J
J
.
′
′
→
%
%
%
x
x
x
n
n
k
k
, 0 =−
%
%
x
A
x
,
%
()
x
N
E
A
∈
−
Из сходимости следует, что ненулевые элементы принадлежат ядру и ортогональному
дополнению :
%
,
%
()xxNEA=∈−
⊥
1 .
Лемма 3.
HTNT
HTNT
=ℜ ⊕
=ℜ ⊕
∗
∗
() ( )
() ()
Доказательство.(первая часть)
Пусть
xNT y T∈∈ℜ
∗
(), (), тогда : (,) (, ) ( ,)xy xTz Txz
=
=
=
∗
0.
Получили :
NT T() ()
∗⊥
⊂
ℜ
.
Пусть
xT∈ℜ
⊥
(), тогда : (,) , ()
x
yy
T
=
∀
∈
ℜ
0 .
(, ) ( ,) ,xTz T x z z H=⇒ = ∀
∈
∗
00.
Значит :
ℜ⊂
=
ℜ
⊕
ℜ
=
ℜ
⊕
⊥∗
⊥
∗
() ( ), () () () ( )TNT HT T TNT и .
Введём обозначения :
T
HHTH H TH H
HH H H
kk
k
() , ( ) ,...,( )
...
=
=
=
⊃⊃⊃⊃
−112 1
12
Лемма 4.
∃≥ =
+
kHH
k
k
0
1
: .
Доказательство.
Предположим противное : пусть такого k не существует.
∀∃∈
⊥
=
+
nxH xH x
kkkk k
:,
1
1.
Возьмём n<m и рассмотрим
Ax Ax
nm
−
.
При этом
Ax x Tx Ax x Tx
nn n mm m
=− =
−
, .
Ax Ax x Tx x Tx
nmn nmm
−=−+− ≥()1.
Из подпоследовательности
x
n
нельзя выбрать фундаментальную подпоследовательность :
Ax
n
- фундаментальна.
Получили противоречие.
Лемма 5.
Пусть
N
T
() {}= 0 , тогда ℜ=()
T
H
.
Доказательство. (совпадает с доказательством 1
-ой
части теоремы).
Предположим противное :
ℜ=
≠
≠
() ,THH HH
121
тогда .
Предположили :
HH
21
=
, т.е. :
Для
∀∈ ∃∈ =f H x H Tx f
11
,:.
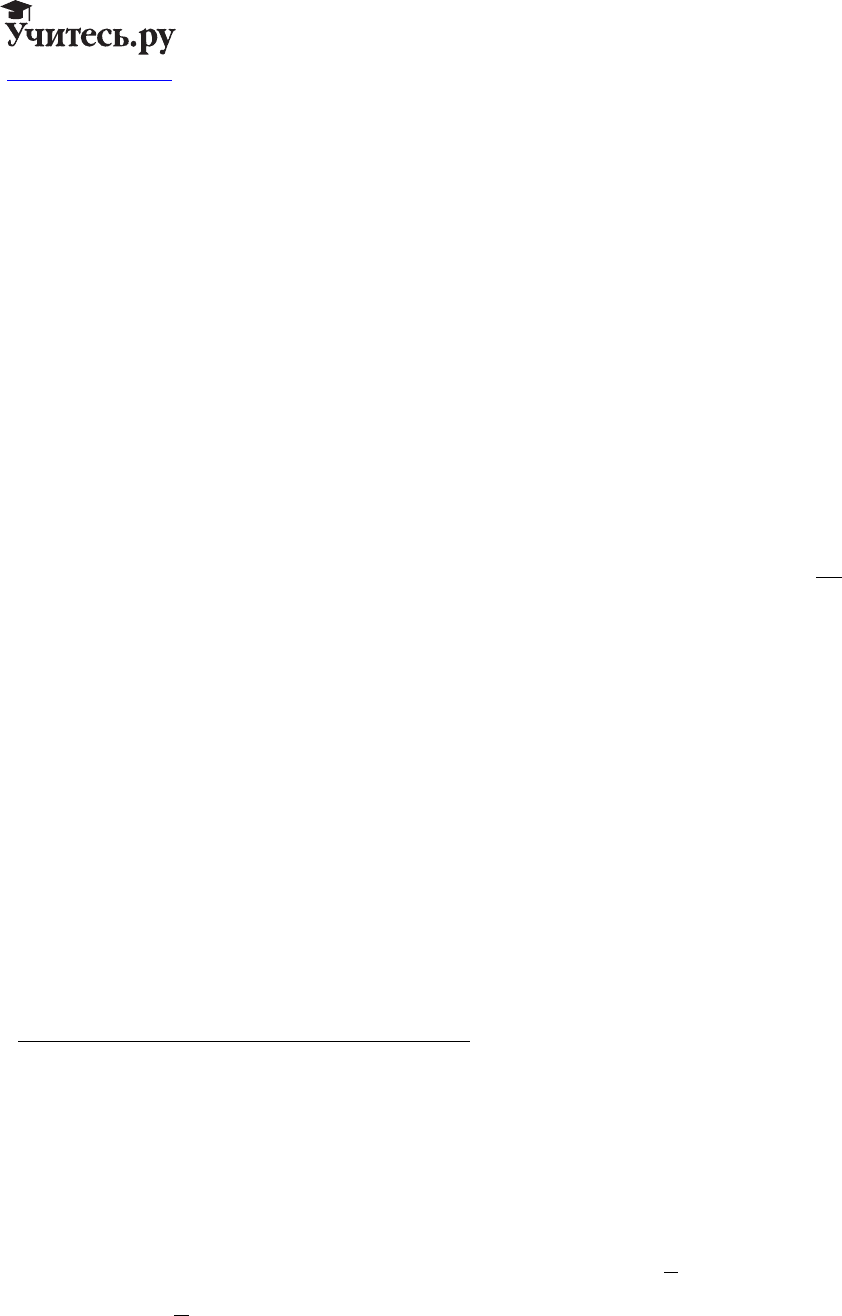
www.uchites.ru
74
Одновременно : для
∀
∈∃
∈
=
f H z H Tz f
1
,:.
Пусть
zHH∈ \
1
T
x
z
x
z
x
z(), ,−= −
=
=00
По индукции :
HH k
k
k
≠∀
+1
, .
Получено противоречие. Лемма 5 доказана.
Лемма 6.
dim ( ) dim ( )NT NT=
∗
.
Доказательство.
Предположим противное, т.е.
nNTmNT=
<
=
∗
dim ( ) dim ( ) .
Обозначим через
( , ,..., )
ϕ
ϕ
ϕ
12 n
- ортонормированный базис в
N
T
().
( , ,..., ) ( )
ψ
ψ
ψ
12 n
NT∈
∗
.
Sx Ix x
ii
i
n
=+
=
∑
(, )
ϕψ
1
.
Если докажем, что оператор S имеет тривиальное ядро, то по лемме 5 получим :
ℜ=()
S
H
.
Пусть
Sx = 0. По лемме 3 получаем Tx x x N T i n
i
==⇒⊥=00 1 и ( , ) ( ), ,
ϕ
.
Если x ортогонален
ϕ
i
для любого i , то :
x
N
S
=
=
00,: {} и .
Можно выбрать
S
xn
=
+
ψ
1
.
Умножим левую и правую части равенства на
ψ
n
+
1
:
Tx x
Sx
Sx
Niin
i
n
n
nnn
,(,)(,)
(, ) ,
(, )( , )
ψϕϕϕ
ψ
ϕψϕ
++
=
+
+++
+=
=
==
∑
11
1
1
111
0
0
1
bg
Значит : n=m.
Доказательство теоремы Фредгольма.
1) доказано по лемме 5 ;
2) доказано по лемме 6 и по лемме 3;
3) доказано по лемме 1 и 6.
Теорема доказана.
UТема. Теорема Гильберта-Шмидта
Пусть
A
H
H
: → , A - самосопряженный, ограниченный оператор; H - унитарное,
бесконечномерное полное сепарабельное пространство.
Лемма 1.
Пусть
A
H
H
: → - самосопряженный, линейный, ограниченный оператор, тогда все
собственные значения - вещественные.
Доказательство.
Пусть
λ
- собственное значение оператора A, соответствующее собственной функции x,
тогда:
λλ λλ
λλ λ
xx xx Ax x xAx x x xx
тк xx R
,, ,, , ,
,.. ,
bgb gb gb gb g bg
bg
=====⇒
⇒= ≠⇒∈0
Лемма 2.
Пусть
A
H
H
: → - самосопряженный, линейный, ограниченный оператор, тогда
собственные функции, соответствующие различным собственным значениям, ортогональны.
Доказательство.
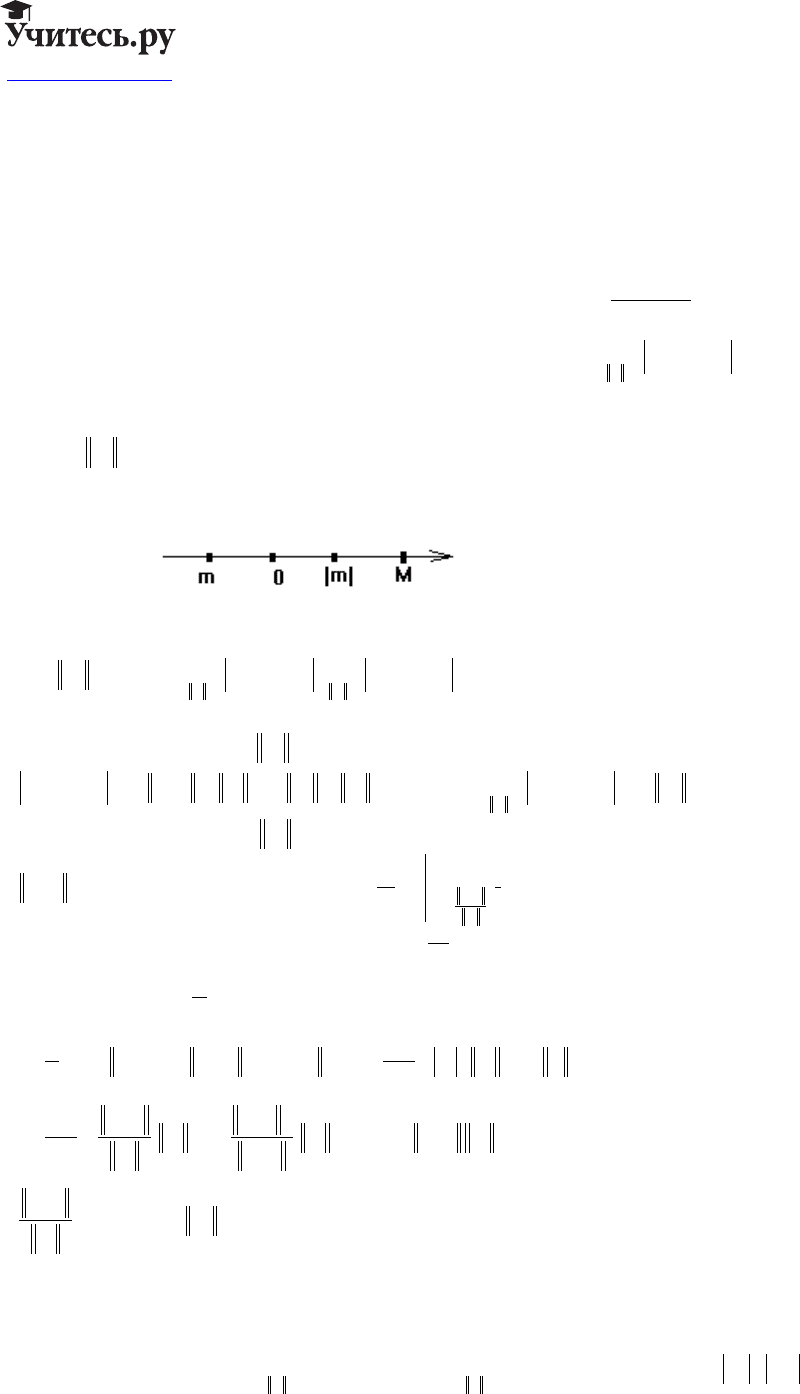
www.uchites.ru
75
Пусть
λ
λ
12
, - различные собственные значения оператора A, соответствующие различным
собственным функциям
xx
12
, , тогда:
λ
λ
λ
λ
λλ
112 112 12 1 2 122 212
1 2 12 12
00
x x x x Ax x x Ax x x x x
xx xx
,,,,, ,
,,
bgbgbgbgbgbg
bgbg bg
==
=
=
=
⇒
⇒− =⇒ =
Значит, собственные функции ортогональны.
Дополнительные обозначения.
Рассмотрим квадратичную форму
Ax x x Ax Ax x,, ,
bgbgbg
== - эрмитова и принимает
только вещественные значения. Обозначим через
C
Ax x
A
x
=
=
sup ,
1
bg
.
Лемма 3.
C
A
A
= - норма оператора равняется супренуму от модуля квадратичной формы.
Пояснение:
,
т.е.
A Ax x Ax x
xx
=
F
H
I
K
==
max sup , , inf ,
11
bgbg
Доказательство.
1) докажем, что:
C
A
A
≤
.
Ax x Ax x A x,
bg
≤⋅≤⋅
2
; отсюда: sup ,
x
Ax x A
=
≤
1
bg
.
2) докажем, что:
C
A
A
≥ .
Ax Ax Ax A x A
x
Axz Ax z x z Ax z x z
Cxz xz
C
xz
C
Ax
x
x
Ax
Ax
x C Ax x
Ax
x
CAC
Ax
x
Ax
z
A
A
A
A
AA
2
22 222
2
2
1
2
1
4
1
42
2
==
F
H
G
I
K
J
F
H
G
I
K
J
=
==++−−−≤
≤+−−= +=
=+
R
S
|
T
|
U
V
|
W
|
=
≤⇒ ≤
=
R
S
|
T
|
U
V
|
W
|
=
,,
,, ,
bgbg
bgchbgchbgch
ns
{}{}
λ
λ
λλλλλ
λλ λ
λ
λ
Лемма доказана.
Обозначим через
MAxx
x
=
=
sup ,
1
bg
mAxx
x
=
=
inf ,
1
bg
C
mM
A
= max ,
ch
.
Лемма 4.
www.uchites.ru
76
Пусть A
H
H
: → - ограниченный, самосопряженный оператор в H, тогда: m и M
принадлежат спектру оператора A:
mAM A
∈
∈
σ
σ
bg bg
, .
Доказательство.
Вместо A рассмотрим A-mE (спектр сдвинется на m, и оператор станет неотрицательным):
(), , , ()AmExx Axx mxx AmE−=−≥⇒
−
≥
bgbgbg
00
Не ограничивая общности рассуждений: оператор A - неотрицательный.
2.
MA∈
σ
bg
- докажем.
∃=xx
nn
lq
:1, и последовательность
δ
n
lq
, что:
δ
n
lq
→ 0 . Рассмотрим:
AMEx AMEx AMEx Ax Mx MAxx
nnnnnnn
−=− −=+− ≤
bgbgbgch bg
2
2
2
2
2,,
(т.к.
AM x== и 1, то член ограничен: Ax A x M M
n
222
22
1≤=⋅= )
≤− −= →→
∞
22 2 0
2
MMM M n
nn
δ
δ
bg
, .
Получено:
x
n
= 1 и норма образа AMEx
n
−→
bg
0 .
A-ME - не может иметь ограниченный обратный оператор.
Определение.
Подпространство
HH
1
⊂ называется инвариантным подпространством оператора A, если
из
xH∈
1
следует Ax H∈
1
.
Лемма 5.
Пусть
H
1
- инвариантное подпространство ограниченного самосопряженного оператора A,
тогда:
H
1
⊥
- ортогональное дополнение к этому подпространству - тоже инвариантное
подпространство того же самого оператора A.
Доказательство.
Пусть
xH∈
⊥
1
; докажем, что Ax H
∈
⊥
1
.
Рассмотрим:
Ax y x Ay,,
bgbg
==0 , где: xH
∈
⊥
1
, y H Ay H
∈
⇒∈
11
.
Лемма доказана.
Лемма 6.
Спектр компактного, самосопряженного оператора состоит из 0 и изолированных
собственных значений конечной кратности.
Доказательство.
1. Докажем, что
0 ∈
σ
A
bg
всегда.
Пусть
0 ∉
σ
A
bg
, тогда существует ограниченный обратный оператор A
−1
.
Возьмем
x ≤ 1 . AA
−
1
переводит шар (не компактное множество) в себя. Получено
противоречие.
2. Рассмотрим
Ax
x
f
Ay y
−=
−=
λ
λ
;
0
Ax
x
f
Ay y
−=
−=
λ
λ
; ( 1 )
( 2 )0
Если
λ
- собственное значение оператора A, то (2) - имеет нетривиальное решение, и (1) -
всегда разрешимо. По теореме Банаха - оператор A имеет ограниченный обратный оператор.
Случай 1: (2) имеет нетривиальное решение, и (1) имеет решение не для всех правых частей,
а только для тех, которые ортогональны решениям (2).
Случай 2:
∃−
−
AE
λ
bg
1
; других ненулевых точек, кроме собственного значения, быть не
может.
3. Докажем: все собственные значения ограничены.

www.uchites.ru
77
Рассмотрим Ax Ax
pq
−
2
, где:
x
p
- собственный вектор, соответствующий собственному значению
λ
p
,
x
q
- собственный вектор, соответствующий собственному значению
λ
q
,
тогда: Ax Ax x x c
pq ppqq pq
−=− ≥+≥
22
22
2
2
λλ λλ
.
Получено противоречие.
Комментарии:
- 0 может быть собственным значением бесконечной кратности, а остальная часть спектра -
из конечного числа собственных значений.
- 0 может не быть собственным значением, но тогда он - точка непрерывного спектра.
Окончательно: спектр состоит из изолированных собственных значений конечной кратности
и 0.
UТеорема Гильберта-Шмидта
Пусть
A
H
H
: → - компактный самосопряженный оператор, тогда существует
ортонормированный базис
xH
n
lq
⊂ , состоящий из собственных функций оператора A.
Доказательство.
Оператор A - ненулевой, следовательно:
A
≠
0 и
C
A
≠
0 .
Значит,
C
A
можно определить как максимум, и m , M- собственные значения. Можно найти
наибольшее по модулю собственное значение
λ
1
. Оно имеет конечную кратность, ему
соответствует некоторое количество собственных векторов.
Проведем процесс ортогонализации, и получим
H
1
- подпространство собственных векторов
оператора A, соответствующих собственному значению
λ
1
. Далее рассмотрим H
1
⊥
- тоже
инвариантное подпространство, и на нем A - компактный, самосопряженный. Если A на
H
1
⊥
не равен 0, на нем рассмотрим
C
Ax x
A
x
,
sup ,
2
1
0=≠
=
bg
. Найдем аналогично
λ
2
и
соответствующее ему
H
2
. Рассмотрим ()HH
12
⊕
⊥
и найдем собственное значение, если
оператор - не 0. В результатет получены
λ
λ
λ
123
≥≥≥L .
Конец:
на каком-то ортогональном подпространстве оператор A обращается в 0, и получена
конечная сумма , т.е.
Ax x H H H H
kk
=∈⊕⊕⊕ =
⊥
+
0
12 1
, L
bg
.
иначе:
HH H
k
12
⊕⊕
⊕
⊕LL - ортогональная сумма подпространств совпадает с H , т.к.
иначе на ортогональной сумме рассматривается ортогональное дополнение, и находится ещё
одно собственное значение.
Возможны 2 случая:
1) ортонормированный базис из элементов подпространств ( в этом случае система
собственных векторов дополнняется до ортонормированного базиса элементами ядра
оператора A):
ee e eeNA
r
k
r
k
j
k
1
11
1
1
,,,,,,,LLL
n
s
bg
⊂ ;
2) бесконечный ортонормированный базис :
ee e e
r
k
r
k
k
1
11
1
1
,,,,,,,LLL L .
Найдите больше информации на сайте Учитесь.ру (HTUwww.uchites.ruUTH)!
