Лекции - Уравнения в частных производных
Подождите немного. Документ загружается.

www.uchites.ru
61
=+∇
=⇒ ≡
zzz
z
ωω
ωω
2
0
2
2
1
2
00
x t dxdt x t dt dx
x t dxdt x t
Q
T
D
Q
T
T
,,
,,
bg bg
bg bg
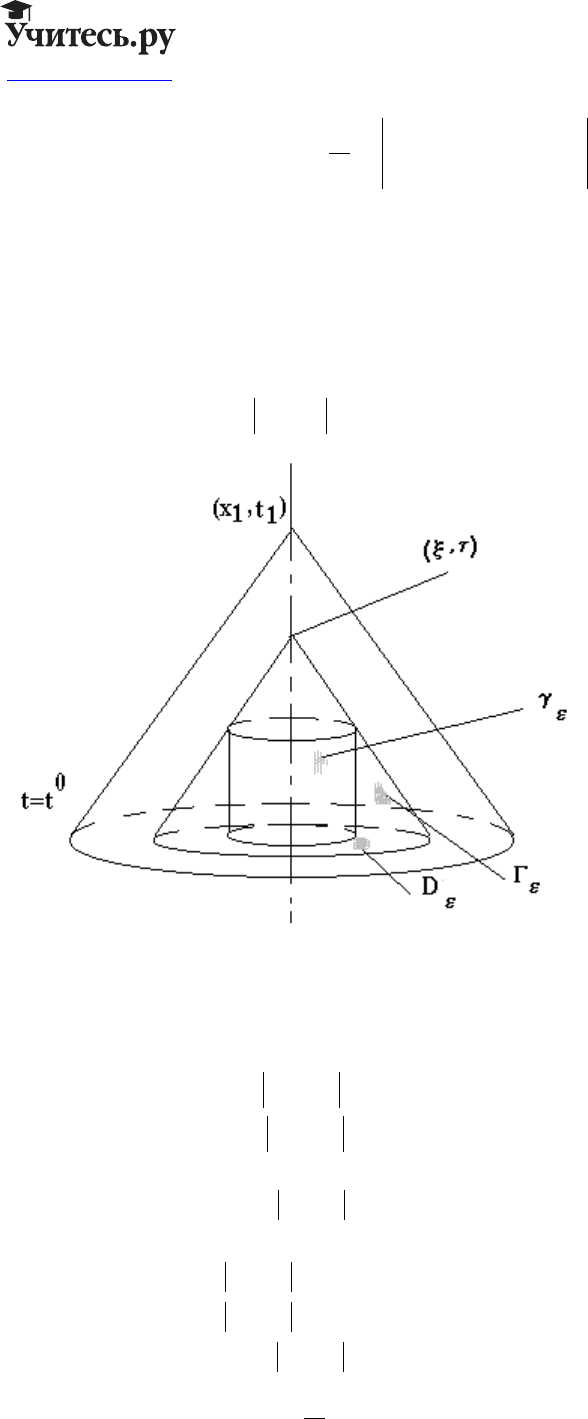
Формула Кирхгофа.
Дополнительные обозначения:
пусть есть
tt
01
< ,
x
1
- фиксируется. Обозначим :
KxtRxxttttt
xtt
110
4110 1
,,
,: ;=∈−<−<<
bg
o
t
- конус с вершиной в xt
11
,
d
i
.
Возьмем произвольную
ξ
τ
,
,,
bg
∈ K
xtt
110
.
Обозначим:
Γ
xtt
xt R x x t tt t t
110
4110 1
,,
,: ;=∈−=−<<
bg
o
t
DxtRxxtttt
xtt
110
41100
,,
,: ;=∈−<−=
bg
o
t
.
Выберем
0
0
<<
−
ε
τ
t и рассмотрим :
KxtR x ttt
ε
εξτ τε
=∈<−<−<<−,: ;
bg
n
s
40
- вне цилиндра, но внутри конуса.
Обозначим через
Γ
ε
- часть конической поверхности, ограниченной K
ε
:
Γ
ε
ξτ τε
=∈−=−<<−xt R x tt t,: ;
bg
n
s
40
γξετε
ε
=∈−=<<−xt R x t t,: ;
bg
n
s
40
DxtR x ttt
ε
εξτ
=∈<−=−=,: ;
bg
n
s
400
uCK CK D∈∩∪
21
bg b g
- дважды непрерывно дифференцируема в открытом конусе. При
этом :
uu uCK
tt
=− ∈∆
ch
- замыкание конуса.
Замечание:
- волновой оператор.
www.uchites.ru
62
Рассмотрим вспомогательную функцию: v
t
x
=
−
−
+
τ
ξ
1.
Рассмотрим:
v u u v vu uv vu uv
xx
x
tt
t
i
ii
i
−=− − +−
=
∑
dibg
1
3
. Заметим: v
x ≠
=
ξ
0 .
В дальнейшем: x принадлежит малому конусу с вырезанным цилиндром.
Проинтегрируем левую и правую части тождества по
K
ε
:
v udxdt vu uv n vu uv n ds
xxi tt
i
DK
ii
=−−+−
R
S
T
U
V
W
=
∪∪
∑
z
z
dibg
4
1
3
Γ
εε εε
γ
,
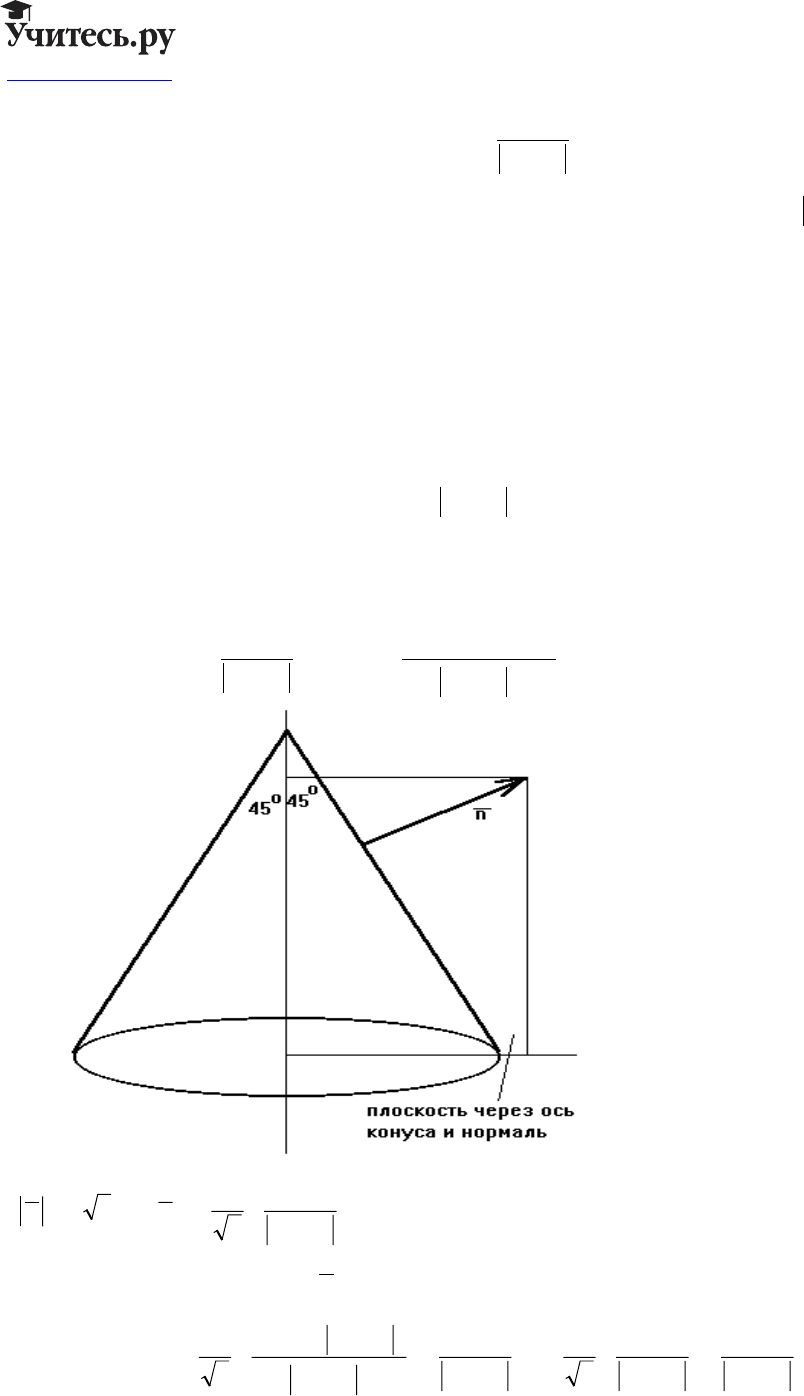
где: - единичный вектор внешней нормали к границе области.
Разобьем этот интеграл на 3 интеграла:
LL L==
z
z
z
II I
D
εε ε
γ
εε ε
12 3
=
Γ
;
потом
ε
→ 0 .
Рассмотрим на конической поверхности
xt
−
=
−
ξ
τ
интеграл
Ivnvnuds
xi t
i
i
ε
ε
34
1
3
=−
F
H
G
I
K
J
=
∑
z
Γ
Вычислим все частные производные функции v по
x
i
и по направлению внешней нормали к
поверхности:
v
x
v
tx
x
t
=
−
∇=
−−
−
1
3
ξ
τξ
ξ
bgb g
nn
x
x
==
−
−
F
H
G
I
K
J
2
1
2
1
ξ
ξ
,
Зная, что
v n grad v n
xi
i
i
=
∑
=
1
3
,
bg
, получим:
vn vn
tx
x
xxx
xi
i
t
i
=
∑
−=
−−
−
−
−
F
H
G
I
K
J
=
−
−
−
F
H
G
I
K
J
=
1
3
4
2
4
1
2
11
2
11
0
τξ
ξ
ξξξ
bg
,
где:
xt,
bg
∈Γ
ε
. Вывод: I
ε
1
0= .
Рассмотрим
I
ε
2
, зная, что для Dn
ε
=
−
000 1,,,
bg
.
www.uchites.ru
63
Iuvvudx
ux t
x
dx u x t
t
x
dx
tt
xt
t
xt
D
ε
εξτ εξτ
ξ
τ
ξ
ε
2
0
0
00
1=− =
−
+
−
−
−
F
H
G
I
K
J
<−<− <−<−
z
z
z
bg
di
di
,
,
Переход к пределу:
lim
,
,
ε
ε
ξτ ξτ
ξ
τ
ξ
→
−<− −<−
=
−
+
−
−
−
F
H
G
I
K
J
z
z
0
2
0
0
00
1I
ux t
x
dx u x t
t
x
dx
xt
t
xt
di
di
Вычислим:
Idtu
v
n
v
u
n
ds I I
t
x
x
ε
τ
ε
ξε
εε
∂
∂
∂
∂
333
0
=−
F
H
G
I
K
J
=
′
−
′′
−
−=
zz
n
x
x
=
−
−
F
H
G
I
K
J
ξ
ξ
,0
- внутренняя
нормаль к цилиндру.
Т.к. u - непрерывно дифференцируема на поверхности, то:
′′
≤
−
+
F
H
G
I
K
J
−
z
IM
t
dt
t
ε
τ
ε
τ
ε
πε
3
2
14
0
∂
∂
ξξ
ξ
τ
τ
ε
v
n
xx
x
t
t
=
−−
−
−=
−
,
bg
bg
4
2
учитывая:
x −=
ξ
ε
на цилиндрической поверхности.
′
=
−
=
−
−+
+−
−
−=
−
−=
−
z
z
z
z
z
I
t
dt u x t ds
t
dt u x t u t ds
tutdt
t
x
x
t
x
x
t
ε
τε
ξε
τε
ξε
τε
τ
ε
τ
ε
ξ
πτξ
3
22
00
0
4
bg
bg
bg
bgbg
bgbg
,,,
,
В силу оценки:
ux t u t C,,
bgbg
−<
ξε
2
Получим:
lim , ,
,
,,
ε
ε
ττ
ξτ
ξτ
τ
ξτ
πτξ
τ
ξ
ξ
τ
ξ
πτξ
→
−<−
−<−
−<−
′
=− +
−
−
+
F
H
G
I
K
J
=
=
−
+
−
−
−
F
H
G
I
K
J
+−
z
z
z
zzz
0
3
0
0
41
14
00
0 0
I t u t dt dt
t
x
ux tdx
ux t
x
dx u x t
t
x
dx t u t dt
tt
xt
xt t
xt
bgbg bg
di
di
bgbg
tutdt uxt
t
x
dx dt
t
x
ux tdx
t
t
xt t
xt
−=
−
−
−
F
H
G
I
K
J
+
−
−
−
F
H
G
I
K
J
z
z
z
z
−<−
−<−
τξ
π
τ
ξπ
τ
ξ
τ
ξτ
τ
ξτ
b gbg bg bg
,, ,
1
4
1
1
4
1
00 0
0
ux t
x
ds dx
ux t
x
ds
utdt
ux t
t
ds u x t
dx
x
dt
ux t
x
dx
x
xt
x
xt
t
x
xt
t
xtt t
xt
,,
,
,
,
,
00
0
0
0
0
00
0
000 0
1
4
1
4
d
i
d
i
bg
di
di
bg
−
=
−
⇒
⇒=
−
+
−
+
−
−<− −=−
−
−=− −<−
−<−
z
z
z
zzzzz
ξξ
ξ
π
τ
ξπ ξ
ξτ ξτ
τ
ξτ ξτ
τ τ
ξτ
u
t
ux t ds
t
uxt ds
dt
ux t
x
dx
x
xt
tx
xt
t
xt
ξτ
∂
∂τ
πτ πτ
πξ
ξτ ξτ
τ
ξτ
,, ,
,
bg
di
di
di
di
bg
=
−
F
H
G
G
I
K
J
J
+
−
+
+
−
−=− −=−
−=−
z
z
zz
1
4
1
4
1
4
0
0
0
0
0 0
0
λ
τ
λτ τλ
=−
=
U
V
W
⇒=− = =
t
tt
t пиt
0
0
0 р
bg
1
4
1
4
0
0
0
π
λ
τξ
ξπ
τξ
ξ
τ
ξλ
ξτ
d
ux x
x
ds
ux x
x
dx
t
x
x
xt
−
−=
−<−
zz z
−−
−
=
−−
−
, ,
ch ch
www.uchites.ru
64
u
t
ux t ds
t
uxt ds
ux x
x
dx
x
xt
tx
xt
xt
ξτ
∂
∂τ
πτ πτ
π
τξ
ξ
ξτ ξτ
ξτ
,, ,
,
bg
di
di
di
di
ch
=
−
F
H
G
G
I
K
J
J
+
−
+
+
−−
−
−=− −=−
−<−
z
z
z
1
4
1
4
1
4
0
0
0
0
0 0
0
Получена формула Кирхгофа: (1)
ux t
t
tt
utds
tt
utds
ux
x
d
xtt
t
xtt
xt
,, ,
,
bg
di
di
di
di
ch
=
−
F
H
G
G
I
K
J
J
+
−
+
+
−−
−
−=− −=−
−<−
z
z
z
∂
∂
π
ξ
π
ξ
π
ξτ ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξτ
1
4
1
4
1
4
0
0
0
0
00
0
Замена переменных (чтобы легче было дифференцировать по t):
ξ
ηξ η
ξη
−
−
==+− =−
x
tt
ztt ds ttds
0
00
2
,,
bg bg
∂
∂π
η
π
η
π
ηη
π
ξξ ξ
η
η
η
η
η
η
ξ
η
t
tt
ux t t t ds ux t t t ds
tt
ux t t t ds
tt
ut xutds
−
+−
F
H
G
I
K
J
=+− +
−
∇+− =
=
−
+−∇
== =
=
z
z
z
z
0
00
1
00
1
0
00
1
0
2
00
1
4
1
44
1
4
bgch bgch bgch
bg
bgb gbg
,, ,
,,
П
родифференцировано первое слагаемое:
′
1
bg
u
tt
ut xutds
tt
utds
ux
x
d
xtt
t
xtt
xtt
ξτ
π
ξξ ξ
π
ξ
π
ξτ ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
,,, ,
,
bg
bg
bgb gbg
di
di
ch
=
−
+−∇ +
−
+
+
−−
−
−=− −=−
−<−
z
z
z
1
4
1
4
1
4
0
2
00
0
0
0 0
0
Геометрический смысл формулы.
1. В первых двух интегралах производится интегрирование по границе основания конуса -
трехмерной сфере.
2. В третьем интеграле производится интегрирование по основанию конуса - трехмерному
шару.
3. Значение даламбериана вычисляется интегрированием по боковой поверхности конуса.
СМЫСЛ. Дважды дифференцируемая функция u(x,t) выражается через значение первых
производных на сфере (границе основания конуса) и
её даламбериан на боковой
поверхности конуса.
UЗадача Коши для волнового уравнения
Обозначим:
txtxRt
txtxRt
n
n
>= ∈ >
≥= ∈ ≥
00
00
lq
bg
n
s
lq
bg
ns
,: ,
,: ,
Определение.
Функция u(x,t) , такая, что:
1)
ux t C t,
bg b g
∈>
2
0 - дважды непрерывно дифференцируемая на t > 0
lq
;
2)
ux t C t,
bg b g
∈≥
1
0 - один раз непрерывно дифференцируемая в замыкании этого
множества;

www.uchites.ru
65
называется классическим решением задачи Коши для волнового уравнения, если:
;
;
;
;,
uf t
u
u
fCt CR
t
t
t
n
=>
=
=
∈> ∈
=
=
02
3
0
0
0
bg bg
bg
bg
di
ϕ
ψ
ϕψ
Пусть n=3.
Обозначим:
Kxttt
xtt
110
00
,,
,: ;=−<−<<
ξτ ξ τ τ
bg
mr
По формуле Кирхгофа функция u(x,t) выражается для любого конуса
K
xt,,0
через функции
f
,,
ϕ
ψ
в этом конусе. Функция u(x,t) однозначно определяется функциями
f
,,
ϕ
ψ
в
любом конусе и, значит, в полупространстве.
Теорема единственности.
Задача Коши (2)-(3) не может иметь более одного решения.
Вопрос существования.
Если классическое решение существует, то оно задается формулой Кирхгофа (4):
ux t
tt
ds
t
ds
ftx
x
d
xt xt
xt
,
,
b g bg bg bg
ch
=
F
H
G
I
K
J
++
+
−−
−
−= −=
−<
z
z
z
∂
∂π
ϕξ
π
ψξ
π
ξξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
1
4
1
4
1
4
4
Таким образом, вопрос о существовании классического решения
сводится к нахождению условий, налагаемых на функции
f
,,
ϕ
ψ
, при которых функция,
стоящая в правой части формулы (4), является решением этой задачи. Получено лишь
достаточное условие.
Предварительные рассуждения.
Введем функцию:
uxt
t
gds
g
xt
,, ,
τ
π
ξτ
ξ
ξ
bg bg bg
=
−=
z
1
4
5
Есть
gx Ct,
τ
bg b g
∈≥0 . Для каждого xRt∈>>
3
00,,
τ
d
i
определяется uxt
g
,,
τ
bg
как
интеграл.
Производится исследование
uxt
g
,,
τ
bg
.
Лемма 1.
Пусть функция g и все её производные по пространственным переменным непрерывны до
порядка k :
Dg C k
x
α
τ
α
∈≥
≤
0
bg
, , тогда:
1) функция и все её производные вплоть до порядка k по x и t непрерывны на множестве
t ≥≥00,
τ
lq
: Du C t k
xt g,
,,
α
τα
∈≥≥ ≤00
lq
ch
2) для
k ≥ 2 и ∀≥
τ
0 функция u
g
удовлетворяет однородному волновому уравнению при и
следующим условиям:
,
u
u
u
ugx
g
g
t
g
t
g
t
t
=
=
=
=
=
=
=
0
0
0
0
0
0
∆
di
bg
τ
Доказательство.
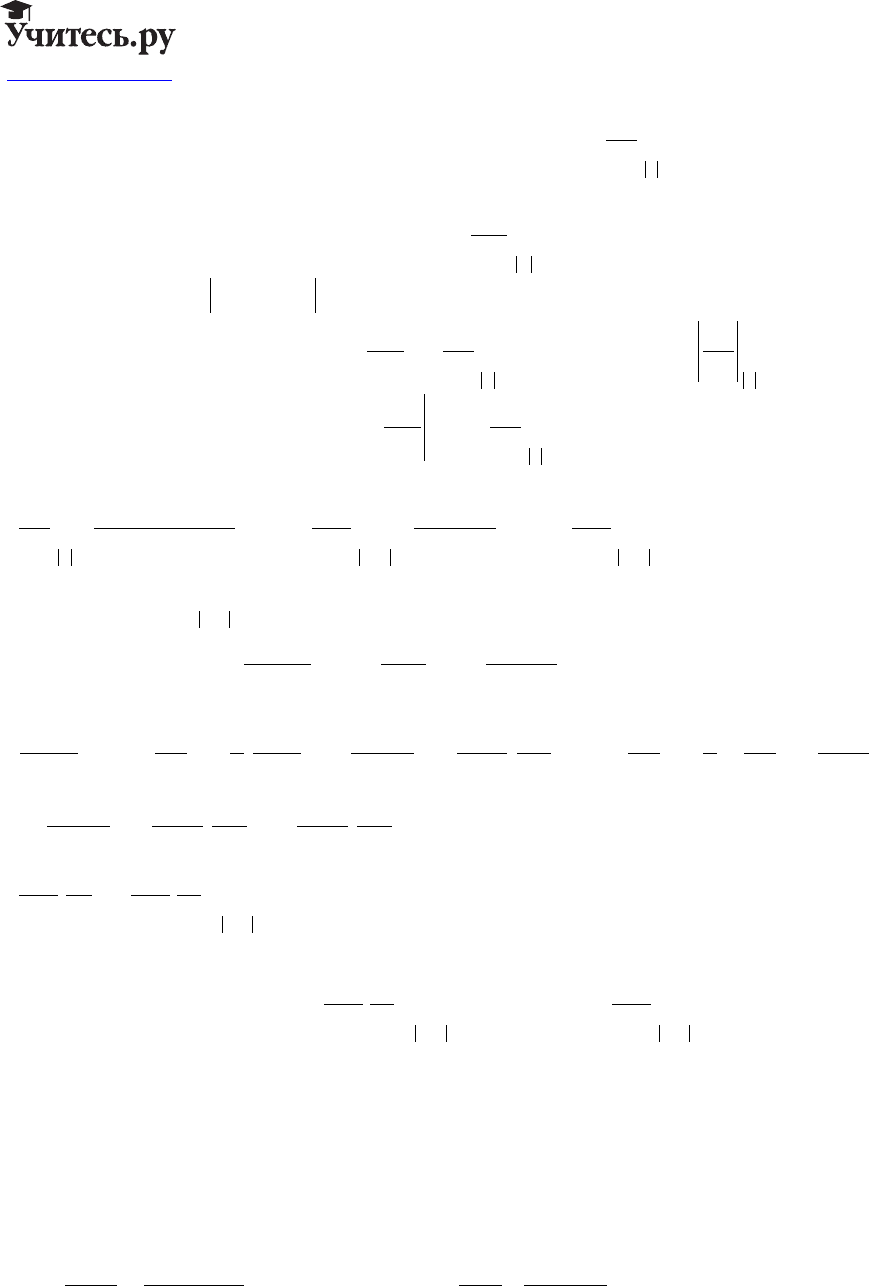
www.uchites.ru
66
В (5) перейдем к новой переменной, тогда: uxt
t
gx t ds
g
,, ,
τ
π
ητ
η
η
bg b gbg
=+
′
=
z
4
1
5
Отсюда следует первое утверждение леммы.
Применим
∆ к u
g
, тогда: ∆∆uxt
t
gx t ds
g
,, ,
τ
π
ητ
η
η
bg b g bg
=+
=
z
4
6
1
Подставим t=0:
uu
g
t
g
t==
==
00
0∆ .
Возьмем производные по t от
u
g
:
∂
∂π
ητ
π
ηητ
η
η
η
η
u
t
gx t ds
t
gx t ds
g
=++∇+
==
z
z
1
44
11
,,
bg bg
.
Рассмотрим производную при t=0:
∂
∂π
ττ
η
η
u
t
ds gx gx
g
t =
=
=⋅=
z
0
1
1
4
,,
bg bg
Преобразуем второе слагаемое:
t
gx t
n
ds
t
gt
n
ds
t
gd
xt xt
4
1
4
1
4
1
π
∂ητ
∂π
∂ξ
∂π
ξτ ξ
η
η
η
ξ
ξξ
+
==
=−=−<
zzz
,,
,
bg bg
bg
∆
обозначим :
Igd
xt
=
−<
z
∆
ξτ ξ
ξ
,
bg
тогда (7) примет вид:
∂
∂
π
u
t
u
t
I
t
gg
=+
4
.
Используем его для вычисления второй производной по времени:
∂
∂
∂
∂ππ
∂
∂π
π
π
∂
∂
π
∂
∂
2
22 2 2
2
1
4
1
4
1
4
4
1
4
1
4
u
t
u
tt
u
t
I
tt
I
t
u
tt
u
t
I
t
I
tt
I
tt
I
t
gg g g g
=− + = + =− + +
F
H
G
I
K
J
−
−+ =
1
4
1
4
π
∂
∂π
∂
∂
ξτ ξ
ξ
t
I
ttt
gd
xt
=
F
H
G
I
K
J
−<
z
∆ ,
bg
Предствляя этот объемный интеграл в виде повторного интеграла: сначала по сфере, а затем
от 0 до t, получим равенство:
1
4
1
4
π
∂
∂
ξτ ξ
π
ξτ τ
ξξ
ξ
tt
gd
t
gds uxt
xt xt
g
∆∆∆,,,,
bg bg b g
−< −=
z
z
F
H
G
I
K
J
==
- вследствие формулы (6) справедливо последнее равенство.
Лемма доказана.
Теорема 2.
Пусть:
ϕ
- трижды непрерывно дифференцируемая в
R
3
:
φ
∈ CR
33
d
i
;
ψ
- дважды непрерывно дифференцируема в
R
3
:
ϕ
∈ CR
23
d
i
;
f
f
x
f
xx
iij
,,
∂
∂
∂
∂∂
2
- непрерывны : f
f
x
f
xx
Ct
iij
,,
∂
∂
∂
∂∂
2
0∈≥
bg
;
тогда: решение задачи Коши (2)-(3) существует и дается формулой Кирхгофа (4).
Доказательство.
www.uchites.ru
67
Рассмотрим второе слагаемое: uxt
ψ
,
bg
в силу леммы 1 есть:
uxt Ct
ut
u
u
t
x
t
t
ψ
ψ
ψ
ψ
∂
∂
ψ
,
,
;
bg b g
bg
bg
∈≥
=>
==
=
=
2
0
0
0
00
0
Рассмотрим первое слагаемое
∂
∂
ϕ
u
t
. T.к.
ϕ
∈ CR
33
d
i
, то: uCt
ϕ
∈
≥
3
0
bg
∂
∂
ϕ
u
t
Ct∈≥
2
0
bg
∂
∂
∂
∂
∂
∂
ϕ
ϕ
u
tt
u
t
===
di
00
Начальные условия:
∂
∂
ϕ
ϕ
u
t
x
t =
=
0
bg
;
∂
∂
∂
∂
∂
∂
ϕϕ
ϕ
t
u
t
u
t
u
t
t
t
F
H
G
I
K
J
== =
=
=
=
0
2
2
0
0
0∆
di
.
Рассмотрим:
Fxt
ft x
x
d
d
ft ds
d
t
f ds u xt d Gxt d
xt x
t
t
xt
f
tt
,
,
,
,,,,,
bg
ch
bg
bg
bg b g b g
=
−−
−
=−=
=
−
=−=
−< −=
−=−
zzz
zz z z
1
4
1
4
4
0
000
π
ξξ
ξ
ξ
π
ρ
ρ
ξρ
τ
πτ
ξτ ττ τ τ τ
ξξρ
ξ
ξτ
ξ
,
где:
uxt Gxt
f
,, ,,−=
τ
τ
τ
bgbg
- обозначение.
В силу леммы 1 G и все её производные по x и t до второго порядка включительно
непрерывны на множестве
tt≥
≤
≤
00;
τ
lq
.
Функция G удовлетворяет:
;,
Gt
GGfxt
t
t
t
=>
==
=
=
0
0
τ
τ
τ
bg
bg
Перейдем к F. F непрерывна вместе со всеми производными по x до второго порядка
включительно в области
t ≥ 0
lq
, и её первая производная по времени непрерывна в этой
области.
Вычислим производную F по t:
FG Gxtd
t
t
t
t
=+
=
z
τ
τ
τ
,,
bg
0
но: G
t
=
=
τ
0 , и:
FGxtd
tt
t
=
z
,,
τ
τ
bg
0
Следует: FCt∈≥
2
0
bg
.
Fxt,
bg
- удовлетворяет волновому уравнению: F
f
=
Fxt,
bg
- удовлетворяет однородным начальным условиям: FF
t
t
t
=
=
=
=
00
0
Окончательно:
u
u
t
uF=++
∂
∂
ϕ
ψ
- удовлетворяет волновому уравнению u
f
= и
начальным условиям:
uu
t
t
t=
=
=
=
00
ϕ
ψ
;. .
Замечание.
Доказательство теоремы о существовании и единственности классического решения задачи
Коши в случае, когда n=3, опиралось на интегральное представление функции в виде
формулы Кирхгофа. Формулы, аналогичные формуле Кирхгофа, можно вывести для
произвольного числа пространственных переменных. Эти формулы дают выражение
достаточно гладкой функции u(x,t) через её первые производные и даламбериан в
конусе.
Пользуясь этим представлением, можно обобщить эти теоремы существования и
единственности для произвольного числа переменных (n>3).
Замечание.
Формулы, аналогичные формулам Кирхгофа для n=1 и n=2, можно получить из n=3 методом
спуска.
www.uchites.ru
68
UМетод спуска (как из формулы Кирхгофа получить формулы Пуассона и
Даламбера)
ux t
t
t
utds
t
utds
ux
x
d
xtt
t
xtt
xt
,, ,
,
bg
di
di
di
di
ch
=
−
F
H
G
G
I
K
J
J
+
−
+
+
−−
−
−=− −=−
−<−
z
z
z
∂
∂
πτ
ξ
πτ
ξ
π
ξτ ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξτ
1
4
1
4
1
4
0
0
0
0
00
0
Надо получить формулу Кирхгофа для n=2 - формулу Пуассона.
Обозначения:
1
2
123 3
123 3
),, ,
),, ,
xxxx xx
=
=
′
==
′
bgbg
bgbg
ξξξξ ξξ
Преобразуем интегралы:
ξ
ξ
3
0
0
22
0
tt
tt x
tt−
=
−−
′
−
′
−
bg
Рассмотрим:
1
2
0
0
22
0
π
ξξ
ξ
ξ
utd
tt x
xtt
,
bg
bg
′
−−
′
−
′
′
−
′
<−
z
Заменим
xx на , на
′′
ξ
ξ
.
Получим формулу:
ux t
t
utd
tt x
utd
tt x
d
ut d
x
xtt
t
xtt
tt
x
(,)
(,)
()
(,)
()
(, )
′
=
′′
−−
′
−
′
F
H
G
G
+
+
′′
−−
′
−
′
+
−
′
−
′
−
′
I
K
J
J
′
−
′
<−
′
−
′
<−
−
′
−
′
<
z
zzz
∂
∂π
ξξ
ξ
π
ξξ
ξ
π
ρ
ξρξ
ρξ
ξ
ξξρ
1
2
1
2
1
2
0
0
2
2
0
0
2
2
0
2
2
0
0
0
Получена формула Пуассона:
www.uchites.ru
69
uxt
t
utd
tt x
utd
tt x
d
ut d
x
xtt
t
xtt
tt
x
(, )
(,)
()
(, )
()
(, )
0
0
2
2
0
0
2
2
0
2
2
1
2
1
2
1
2
0
0
0
=
−−−
F
H
G
G
+
+
−−−
+
−
−
′
−
′
I
K
J
J
−<−
−<−
−
′
−
′
<
z
zzz
∂
∂π
ξξ
ξ
π
ξξ
ξ
π
ρ
ξρξ
ρξ
ξ
ξξρ
Формула Даламбера:
ux t
ux t t t ux t t t
utd d u d
t
xtt
xtt
t
t
xt
xt
,
,,
,,
bg
bgbg
bg bg
=
+− + −+
++
−+
+−
−+
+−
zzz
00
0
2
1
2
1
2
0
0
0
ξξ τ ξτξ
τ
τ
Обозначим:
Lu x t
u
t
u(,)=−
∂
∂
∆ .
Введём фундаментальное решение уравнения теплопроводности:
Uxt
t
e
Ux x t t
tt
e
n
x
t
n
xx
tt
(,)
(,)
()
()
=
−−=
−
−
−
−
−
1
2
1
2
2
0
2
0
4
00
0
4
π
π
ej
ej
Свойства U для уравнения теплопроводности:
1.
LU t t
xt,
()=>0
0
2.Если U продолжить тождественным 0 при
(, , )ttx xtt
≤
≠
≠
000
, то такая функция U
C
∈
∞
-
бесконечно дифференцируема.
Доказательство.
Если выписывать производные функции U, то получится рациональная функция,
умноженная на экспоненту, экспонента стремится к 0 быстрее любой рациональной
функции, значит, пределы все равны 0, и получена бесконечная гладкость.
3.
Ux x t t dx
R
n
(,)−− =
z
00
1
Доказательство.
Ux x t t dx e d
R
xx
tt
n
R
n n
(,)
()
−− = =
z
z
=
−
−
−
00
2
0
0
2
1
1
введём замену :
η
η
π
η
В качестве упражнения:
edt
t−
−∞
∞
z
=
2
π
.
4.
LUxxtt
xt
00
00
0
,
*
(,),−−=

www.uchites.ru
70
где L
tx
xt
i
i
n
00
0
2
1
,
*
−−
=
∑
∂
∂
∂
∂
- формула представления решения задачи Коши для
уравнения теплопроводности.
Дополнительные обозначения.
Пусть
uC t T C t T∈<<∩<<
21
00
,
()(), пусть u, Lu - ограничены в полосе.
Введём
ξ
N
n
CR∈
∞
&
(), обладающую свойством:
01
1
01
≤
≤
=≤
=≥+
ξ
ξ
ξ
N
N
N
x
xxN
xxN
() ;
() ( ),
() ( ),
grad ( )
()
ξ
ξ
N
N
xC
xC
≤
≤
U
V
|
W
|
0
0
∆
- используются срезающие функции.
Lu Lu u u
U x t xLuxt x uxt xuxt
U x tL xuxt xuxt
LxtUxtxuxt
xuxtU x t U
NN N N
NNN
NN
xt N t
Nx
i
(,)
( , ) ( ) ( ,) ( ) ( ,) ( )( ,)
( , )( ()(,)) ()(,)
(,)((,)()(,))
(()(,) ( , ) (
,
*
ξ
ξ
ξ
ξ
ξτ ξ ξ ξ
ξτ ξ ξ
ξτ ξτξ
ξξτξ
=⋅−∇∇−
−−⋅ −∇ ∇ − =
=−− −
−−= −− +
+−−−
2
2
∆
∆
−−
=
∑
xt xuxt
Nxx
i
n
ii
, ))( ( ) ( , )) )
τξ
1
n - размерность постранства
R
n
.
N - определяет область интегрирования.
Будем считать:
ε
τ
ε
<<−
<+
t
xN1
- интегрирование по цилиндру.
dt U x t x Lu x t dx
Ux xLux dx Ux xLuxdx
dt U x t x u x t dx dt U x t x u x t dx
Ux
N
xN
N
xN
N
xN
N
xN
N
xN
N
(,)()(,)
( ,)()(, ) ( , )()(,)
(,)()(,) (,)()(,)
(,)
ξτξ
ξεξ τε ξτεξ ε
ξτ ξ ξτ ξ
ξεξ
ε
τε
ε
τε
ε
τε
−− =
=− −−−− +
+−−∇∇+−− =
=−
<+
−
<+ <+
<+
−
<+
−
z
z
zz
zzzz
1
11
11
2 ∆
() (, ) ( , ) () (,)
( , ) ( )(,) ( , ) ( )(,)
,, ,, ,, ,,
xLux dx U x xLux dx
dt U x t x u x t dx dt U x t x u x t dx
IIII
xN
N
xN
N
xN
N
xN
NNNN
τε ξ τεξ ε
ξτ ξ ξτ ξ
ε
τε
ε
τε
εεεε
−− −− −
−∇−−∇ − −− =
=−−−
<+ <+
<+
−
<+
−
zz
zzzz
11
11
0243
2 ∆
Сначала рассмотрим интеграл:
U x t x Lu x t dx C U x t dx C
N
RR
n n
(,)()(,) (,)
ξτξ ξτ
−− ≤ −− =
zz
00
Можно применить теорему Лебега о предельном переходе под знаком интеграла:
