Лекции - Уравнения в частных производных
Подождите немного. Документ загружается.


www.uchites.ru
51
uCQ CQ CQ D
TT T
∈∩∩∪
21
bg ch c h
0
uCQ
T
∈
2
ch
vCQ
T
∈
1
ch
: v
Г
T
= 0 , v
D
T
= 0
Умножим обе части на v и проинтегрируем по цилиндру:
u u vdxdt fvdxdt
u v u v dxdt u vdx u vdx
u
n
vdxdt fvdxdt
tt
QQ
tt
Q
t
D
t
DQ
TT
TTTT
−=
∇∇ − + − − =
zz
zzzzz
∆
bg
bg
0
∂
∂
Г
∇∇ − = +
z
z
z
u v u v dxdt fvdxdt vdx
tt
QDQ
T
T
bg
ψ
0
(5)
Хотя обобщенное решение - общее понятие, но классическое решение
может не быть обобщенным.
Определение.
Обобщенное решение - функция u из
′
HQ
T
() - называется
обобщенным решением задачи (1)-(4), если
u
Г
T
=
0 u
t
=
=
0
ϕ
и для
∀∈
′
vHQ
T
(), такого, что v
D
T
= 0 и v
Г
T
=
0 выполняется интегральное
тождество (5).
Существование обобщенного решения первой смешанной задачи для волнового уравнения.
uufxt
tt
−=∆ (,) (,)xt Q
T
∈
(1)
u
T
Г
= 0 (2)
ux
t =
=
0
ϕ
() (
x
D
∈
) (3)
∂
∂
ψ
u
t
x
t =
=
0
() (
x
D
∈
) (4)
fLQ
T
∈
2
(), j
H
D∈
′
()
ψ
∈ LD
2
()
−=∆ee
x
λ
() xD
∈
bg
(6)
e
Q
∂
= 0 (7)
D
R
n
⊂ - ограниченная область;
∂
QC
∈
1
0
12
<≤≤ ≤ ≤
λ
λ
λ
.......... ...
k
e
11
и
λ
, e
22
и
λ
, ... , e
s
s
и
λ
e
k
k
λ
R
S
|
T
|
U
V
|
W
|
- базис,
тогда:
ψ
ψ
() ()xex
k
k
k
=
∑
ψψ
ψψ
kk
D
LD
k
k
xxexdx() () ()
(
=
=
z
∑
2
2
2
)
ϕ
ϕ
() ();xex
k
k
k
=
∑
где:
ϕϕ
kk
D
xe xdx=
z
() ()
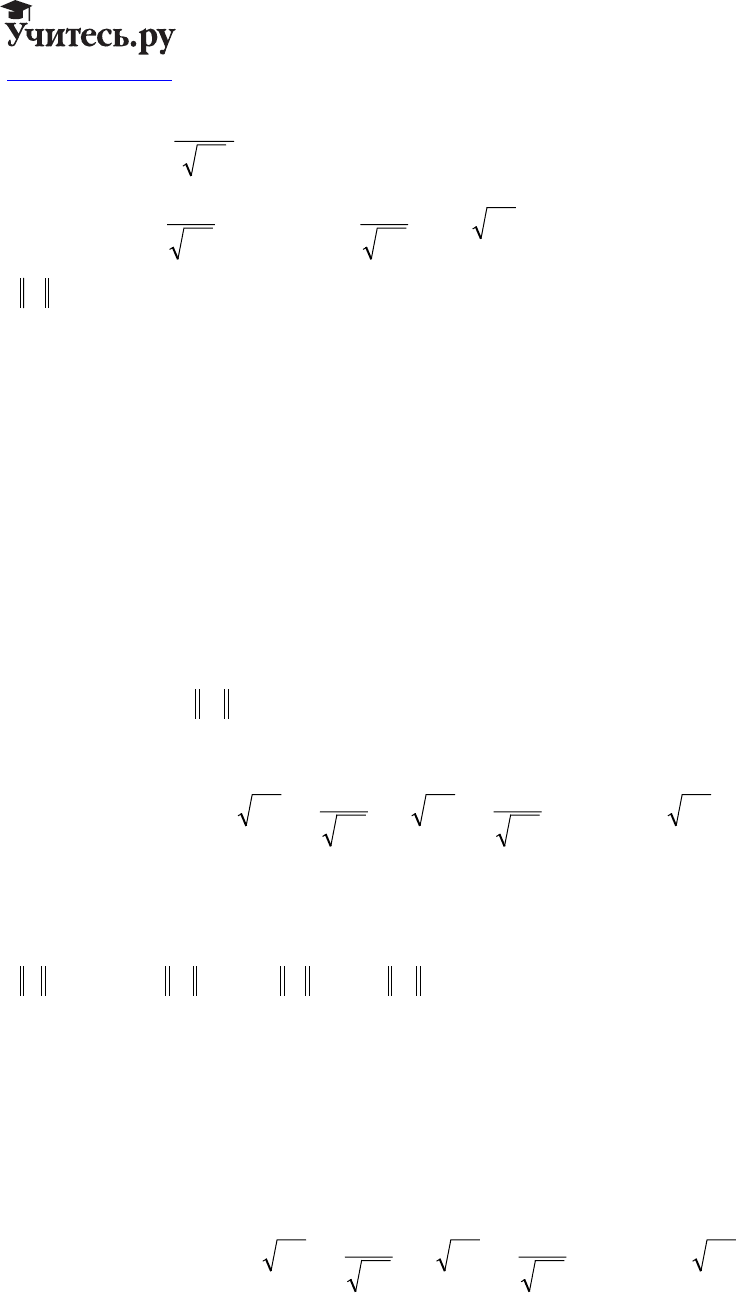
www.uchites.ru
52
ϕϕ
λ
ϕϕ
λ
λϕ
λ
λϕ
ϕϕλϕ
()
%
()
;
%
%
&
()
x
e
x
e
dx
e
dx
k
k
k
k
k
k
k
k
k
k
kk
HQ
k
k
k
k
k
=
=∇∇
F
H
G
I
K
J
==
==
∑
zz
∑∑
′
DD
2
2
2
По теореме Фубини:
fxt f te x
ft fxtexdx
ft fxtdxexdx
f t dt f x t dxdt
k
k
k
kk
kk
k
T
Q
T
,()();
() ( , ) ( )
() ( , ) ( )
() ( , )
bg
=
=
≤
≤
∑
z
zz
zz
D
DD
22 2
2
0
2
ft fxtdx
f t dt f
k
k
k
T
k
LQ
T
22
2
0
2
2
() ( , )
()
()
=
=
z
∑
z
∑
D
ux t t t f t d e x
k
kk
k
k
k
k
kk k
T
( , ) { cos sin ( ) sin ( ) } ( )=++ −
∑
z
ϕλ
ψ
λ
λ
λ
τλττ
1
0
(8)
Теорема.
∀∈fLQ
T2
(),
ϕ
∈
′
&
(HD),
ψ
∈ LD
2
() ряд (8) сходится в пространстве
′
HQ
T
() и сумма
этого ряда является обобщенным решением задачи (1)-(4). При этом имеет место оценка:
uCf
HQ LQ H L
TT
′′
≤++
() ()
&
() ()
22
ϕψ
DD
e
j
(9)
Доказательство.
Первый этап.
Пусть:
f
x
t
f
te
x
xex
xex
kk
kk
k
k
(,) () ();
() ();
() ();
=
=
=
ϕϕ
ψψ
Докажем, что тогда решение u(x,t) имеет вид:
ux t u x t u te x
ut tftd
kkk
kk k
k
k
k
k
kk
T
(,) (,) () ()
cos sin ( ) sin ( )
==
=+ + −
z
ϕλ
ψ
λ
λ
λ
τλτ
τ
1
0
′′
+=Ut Ut ft
k
k
k
k
() () ()
λ
(10)
U
k
k
()0 =
ϕ
(11)
′
=U
k
k
()0
ψ
(12)

www.uchites.ru
53
∇∇−
′
=
=∇∇−
′
=
z
zzzz
u t e x v x e x u t v x dxdt
u t dt e vdx e x dx u t v x t dt
kk k kt
Q
kk
T
kkt
T
T
() () () () ()()
() ( ) () ( , )
bgch
DD
t
00
при почти всех t
vHD
∈
′
&
()
T
.
=+−+
+
′
=+
+
z
z
z
z
zz
z
u t dt e vdx e x dx f t u t vdt
e x u v x dx f t e x v x t dxdt
exvx dx
kkk k kkk
TT
kk kk
Q
kk
T
() ( ) () ()
() ()(,) () ()(,)
()(,)
λλ
ψ
DD
Д
D
t
bg
00
00
0
Доказано:
если
f
x
t
f
te
x
xex
xex
kk
kk
k
k
(,) () ();
() ()
() ()
=
=
=
ϕϕ
ψψ
, то: utex
k
k
() ( ) - решение.
ut t t f t d
kkk
k
k
k
k
kk
t
( ) cos sin ( ) sin ( )=+ + −
z
ϕλ
ϕ
λ
λ
λ
τλττ
1
0
Второй этап.
fxt f xt f te x
xx ex
xx ex
Nkk
k
N
Nkk
k
N
Nkk
k
N
(,) (,) () ();
() () ();
() () ()
==
==
==
=
=
=
∑
∑
∑
1
1
1
ϕϕ ϕ
ψψ ψ
то:
Sxt utex
Nkk
k
N
(,) () ()=
=
∑
1
-обобщенное решение смешанной задачи.
Третий этап.
Докажем, что решения смешанной задачи со специальной правой частью сходятся к
обобщенному решению.
Осуществляется предельный переход:
Оценим
ut
k
() и их производные:
ut f d
ut C f d
kkk
kk
k
T
kk
k
kk
k
T
() ( ) ;
() ( ( ) );
≤+ +
≤++
z
z
ϕψ
λλ
ττ
ϕ
ϕ
λλ
ττ
11
1
0
2
1
2
2
2
0
′
≤++
′
≤++
F
H
G
I
K
J
z
z
ut f d
ut C f d
kkkkk
T
kkkkk
T
() ( ) ;
() ( )
2
0
2
1
222
0
ϕλ ψ ττ
ϕλ ψ τ τ
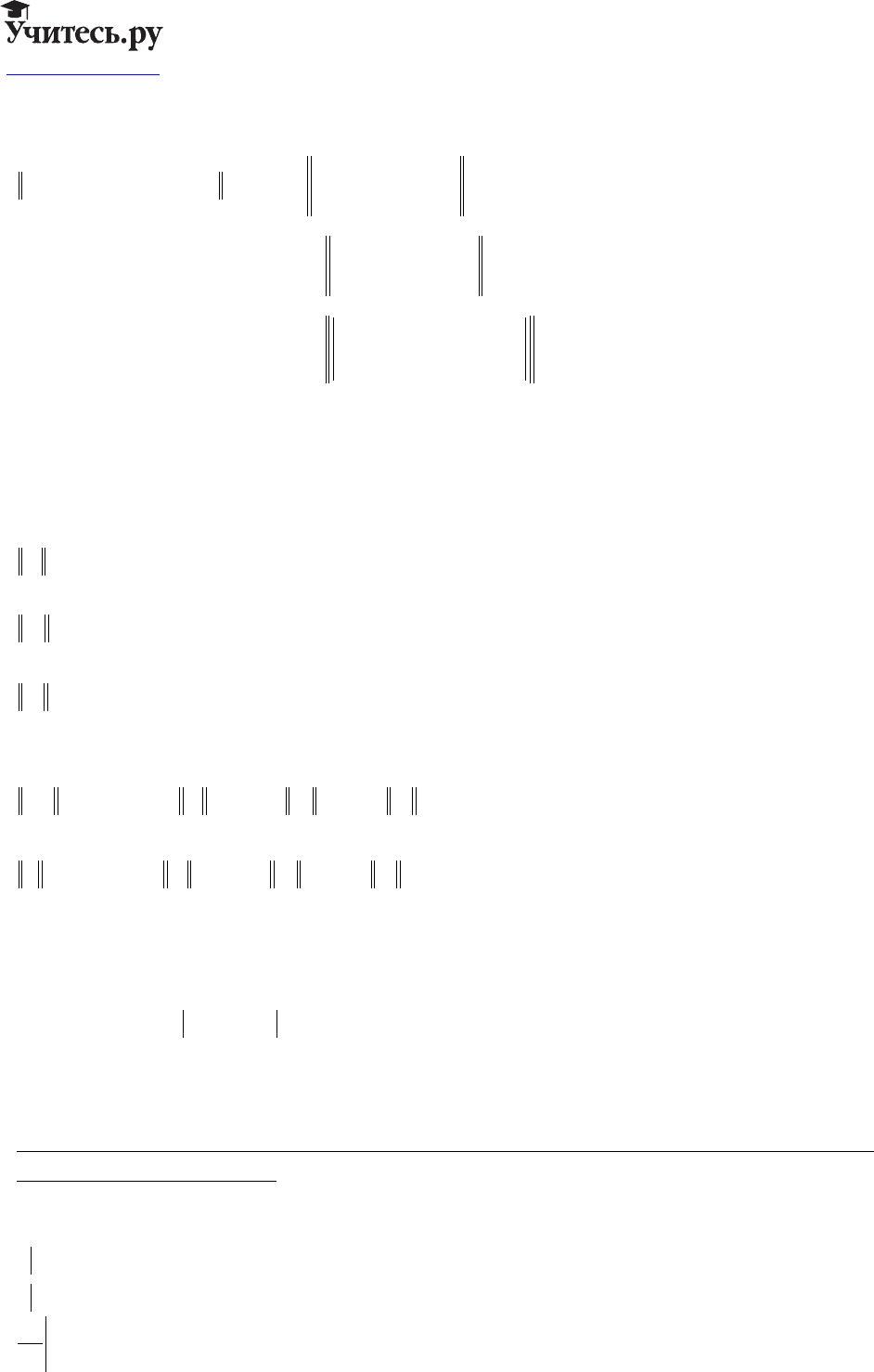
www.uchites.ru
54
Докажем, что последовательность фундаментальна.
Пусть N>M ; рассмотрим :
Sxt S xt utex
dt u t e x dx u t e x dt
dt u t e x dx u t e x dt
NM
HQ
kk
kM
N
HQ
kk
kM
N
T
kk
kM
N
H
T
kk
T
kk
kM
N
T
L
T
T
(,) (,) () ()
() ( ) () ( )
() ( ) () ( )
()
()
()
()
−= =
′
F
H
G
I
K
J
+=
′
F
H
G
I
K
J
+∇
F
H
G
I
K
J
=
′
=+
′
=+ =+
′
=+
∑
∑
zz
∑
z
∑
zz
∑
z
2
1
2
1
0
2
1
2
0
0
2
1
0
2
2
Д
Д
k=M+1
N
Д
Д
T
T
T
T
′
+≤
≤++
F
H
G
I
K
J
=+ =+
=+
∑
z
∑
z
z
∑
ut dt ut dt
Cfd
k
kM
N
T
kk
kM
N
T
kk k k
T
kM
N
() ()
()
bg
2
1
0
2
1
0
2
222
0
1
λ
ϕλ ψ τ τ
ϕλϕ
ψλψ
τ
τ
′
=
=
=
′
=
∞
′
=
∞
′
=
∞
∑
∑
z
∑
&
()
&
()
&
()
;
;
()
H
kk
k
H
kk
k
HQ
k
T
k
ffd
T
D
D
2
2
1
2
1
2
2
0
1
Значит
S
n
lq
n=1
∞
-фундаментальная в
′
HQ
T
bg
- полном , т.е. Su
n
→ .
SC f
uC f
N
HQ
H
LLQ
HQ
H
LLQ
T T
T T
′
′
′
′
≤
′
++
F
H
G
I
K
J
≤
′
++
F
H
G
I
K
J
()
&
(
(()
()
&
(
(()
;
2
2
2
2
2
2
22
22
ϕψ
ϕψ
D)
2
D)
2
D)
2
D)
2
Надо доказать, что u - обобщенное решение, если
S
n
lq
n=1
∞
-обобщенное решение.
∇∇− = +
z
z
z
S v S v dxdt f vdxdt x v x dx
NNt
Q
N
Q
N
t
T
T
di
ψ
()(,)
D
0
∀∈
′
==vHQv v
T
(): ,
D Г
TT
00
e
j
; при переходе к пределу получим:
∇∇ − = +
z
z
z
u v u v dxdt fvdxdt x v x dx
tt
bg
QQD
TT
ψ
()(,)0
UЕдинственность обобщенного решения первой смешанной задачи для
волнового уравнения
uufxt
tt
−=∆ (,) xt Q
T
,
bgch
∈ (1)
u
Г
T
= 0 (2)
ux
t =
=
0
ϕ
() xD
∈
bg
(3)
∂
∂
ψ
u
t
x
t =
=
0
() xD
∈
bg
(4)

www.uchites.ru
55
uHQ
T
∈
′
()
∀
∈
′
vHQ
T
()
vv
Г D
TT
==00;;
∇∇ − = +
z
z
z
u v u v dxdt fvdxdt vdx
tt
QQ
T
T
bg
ψ
D
0
Теорема 1.
Задача (1) - (4) может иметь не более одного обобщённого решения.
Доказательство.
Достаточно убедится, что однородная задача будет иметь единственное решение.
∇∇ − = ⎯ →⎯⎯⎯=
z
u v u v dxdt u
tt
Q
T
bg
00
?
Возьмем:
vx t
ux d t
tT
t
(,)
(,) ,
,
=
<<
≤≤
R
S
|
T
|
z
θθ τ
τ
τ
0
0
где:
τ
- произвольная, 0 <<
τ
T
.
vuxt t
vuxd
t
t
=− < <
∇= ∇
z
(,),( )
(,)
0
τ
θθ
τ
Интегральное тождество приобретет следующий вид:
dx u x t dt u x d dx u x t u x t dt
I dx u x t dt u x d I dx u x t u x t dt
Idx
du
dt
dt u dx
t
t
t
t
∇∇+ =
=∇ ∇ =
==≥
z
z
z
z
z
zzzzz
zz z
(,) (,) (,)(,)
(,) (, ) ; (,)(,) .
00
1
0
2
0
2
2
0
2
0
1
2
1
2
0
τ
τ
τ
ττ τ
τ
θθ
θθ
τ
DD
DD
DD
I dxuxd uxtdt dxuxtdtuxd dxuxd uxtdt
I u x t dt dx u x t dt
udx u
t
1
00000
1
0
2
0
2
20
00
=∇ ∇ =∇ ∇ −∇ ∇
=∇ ∇ =
=→≡
z
z
z
z
z
z
z
z
z
zzz
z
(, ) (,) (,) (,) (, ) (,)
(,) ; (,) ;
θθ θθ θθ
τ
θ
τ
τ
τ
τ
ττ
DDD
D
D
T
Те
орема доказана.
UАнизотропные пространства Соболева
Определение.
Анизотропным пространством Соболева
HQ
T
10,
() называется множество функций
uLQ u LQ
Tx T
i
∈∃∈
22
(): ()
n
s
.
Вводится скалярное произведение:
(, )
,
()
u v u v uv dxdt
HQ
Q
T
T
10
=∇∇+
z
bg
(1)
Свойства пространств:
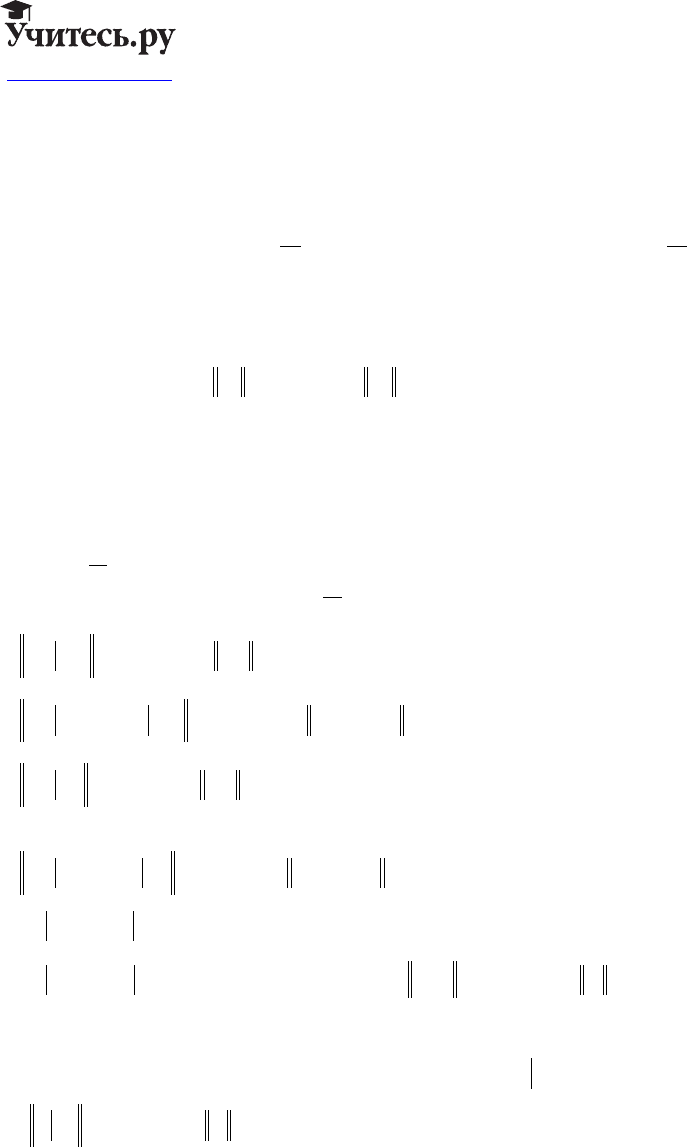
www.uchites.ru
56
Теорема.
Пространство
HQ
T
10,
() -полно.
Доказательство.
Фундаментальная последовательность, переход к пределу в интегральном тождестве.
Пусть
abT<>⊂
′
0, , D D через
′
=
′
×
⇒⊂
′
QDab QQ
TTT
(, ) .
Теорема 2.
∀∈ ∃ ∈
′
∈
⊂
′
≤
′
fHQ FHQ Fx fx
FQ F Cf F f
TT
T
HQ HQ
TT
10 10
10 10
,,
() ()
() () );
;
,,
: ( ) = ( ) (x Q
- продолжение .
T
supp
Теорема 3.
HQ
T
10,
() -сепарабельно.
Доказательство - продолжение функции до финитной.
Теорема 4.
CQ
T
∞
() всюду плотно в HQ
T
10,
() . Возьмем
∀∈ ∃ ∈
′
→uHQ u CQ u uHQ
T
k
T
k
T
10 10, ,
() () () таких : в .
uCu
uu Cuu
uCu
k
D
LQ
k
H
k
D
m
L
km
HD
k
L
k
H
T
T
T
T
∂
∂
∂∂
∂
ττ
ττ
τ
τ
2
2
2
10
2
2
2
2
2
2
()
()
()
()
()
()
,
≤
−≤−
≤
′
′
D
D
D
Г
Г
Q
uu Cuu
uu uu
uu u Cu
km
L
km
H
km km
k
L
H
TT
T
T
TT
TT
T
T
T
ГГ
Г
Q
ГГ
ГГ
Г
Г
Q
Переход к пределу :
−≤−
−→−→
→≤
2
10
2
10
2
2
2
2
00
()
()
()
()
,
,
;
Теорема 5.
Для
∀∈uH
T
10,
()Q можно определить след : uL
T
T
Г
Г
∈
2
() и при этом:
Г
Г
Q
uCu
T
T
T
L
H
2
10
2
1
()
()
,
≤ .
Обобщенные решения смешанной задачи для уравнения
теплопроводности

www.uchites.ru
57
uufxt xtQ
u
ujx xD
uCQ CQ D
uCQ
tT
t
T
xy
t
TT
T
T
−= ∈
=∈
∈∩∪∪
∈
=
∆ (,)
()
() ( )
()
, ( )
= ( )
( )
Г
Г
,
,
bg
1
02
3
0
21
1
0
21
дважды
непр.- диф.
по ,,
раз по
непрерывна в замыкании
цилиндра без верхней
крышки
v ∈
==
−=
−+∇∇ − =
∇∇ − = +
zz
zzz
zzz
C
u(x, 0)v(x, 0)dx
()(,)
1
Г D
D
TT
()Q
vv
u v uv dxdt fvdxdt
uv u v dxdt fvdxdt
u v uv dxdt fvdxdt x v x dx
T
t
QQ
t
Q Q
t
QQD
TT
T T
T
T
00
04
∆
bg
bg
bg
на боковой пов - ти интегралы в О , и:
( )
ϕ
Определение.
Обобщенное решение
uHQ
T
∈
10,
() - называется обобщенным решением задачи (1)-(3),
если
∀∈vHQ
T
1
() : vv
Г D
TT
=
=
00 выполняется интегральное тождество
(4).
UСуществование обобщенного решения первой смешанной задачи для
уравнения теплопроводности (метод Фурье, метод разделения
переменных)
uufxt
x
D
t
t
D
−= ∈
=∈
∈
=
=
∆
∆
(,)
()
x, t Q (1)
u = 0 (2)
u x D (3)
- e(x) = e(x) x (4)
e
T
Г
T
bg
0
0
ϕ
λ
∂
(5)
λ
λ
λ
12
, ,......., ,.....
S
- собственные значения;
ee e
v12
, ,........., ,...... - ортогональный базис в
&
HD
1
();
l
l
l
S
S
1
1
2
2
λλ λ
, ,...., ,... - ортонормированный базис в
&
HD
1
().
www.uchites.ru
58
Будем считать:
ϕ
∈∈LD f LQ
T22
(() )
ϕϕ ϕϕ
==
==
=
∞
=
∞
∑
z
∑
z
ss
s
ss
D
ss
s
ss
D
exexdx
fxt ftex ft fxtexdx
1
1
() ()
(,) () (), () (,) ()
при почти всех t интегрируема с квадратом в
LD
2
( ).
Равенство Парсеваля:
ϕϕ
LD
s
s
2
2
2
1
(
)
=
=
∞
∑
f-измерима и ft f xtdx
s
() ( , )
2
2
≤
z
D
по неравенству Гельдера.
ft fxtdx exdx
s
s
D
s
D
2
1
22
1() ( , ) ( )
=
∞
∑
zz
== .
По теореме Лебега можно слева и справа проинтегрировать по t и поменять местами
∑
z
и .
f t dt f
s
T
s
LQ
T
()
()
0
1
2
2
z
∑
=
∞
=
Решение имеет вид:
u(x, t) =
s
s=1
ϕττ
λλτ
eefdex
ux t u te x
ss
tt
s
T
s
ss
s
−−−
∞
=
∞
+
R
S
T
U
V
W
=
z
∑
∑
()
() ( )
(,) () ()
0
1
Надо доказать сходимость в
H
10,
().
Теорема.
∀∈
∀∈
U
V
W
fLQ
LD
T2
2
()
()
ϕ
ряд (6) сходится в пространстве HQ
T
10,
() к некоторой функции
uHQ
T
∈
10,
(), которая является обобщенным решением задачи (1)-(3). При этом:
uCf
H Q LQ LQ
TTT
10
22
,
() () ()
≤+
ϕ
( 7)
Доказательство.
Первый этап.
Предположим, что правая часть уравнения имеет вид:
fxt ftex
s
s
(,) () ()
=
, а начальная
функция:
ϕ
ϕ
() () () ()xex utex
s
s
s
s
=
=
u
s
.
Рассмотрим:
∇∇− = ∇ ∇ +
′
+=
−−−−−−−−−
−
−−−−−−
−
−
−
−
−
−
−
−
−
−
−
−
−
z
z
z
zzz
u v u v dxdt u t dt e x v x t dx
exdx utvxtdt u exvx dx
sst
Q
s
T
s
ss
T
ss
T
bg
() ( ) ( , )
() ()(,) () ()(,)
0
0
00
D
DD

www.uchites.ru
59
vHQ v HD t
vvHD
u t dt e x v x t dx
T
D
t
D
t
s
T
ss
D
t
Tt
∈⇒∈ ∀
=⇒∈
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
=+
−−−−−−−−−
−
−−−−−−
−
−
−
−
−
−
−
−
−
zz
11
1
0
0
() ()
()
() ( )( , )
,
Г
λ
По построению (,) удовлетворяет :
u
x
t
uuft u
e x dx f t u t v x t dt
e x v x t dx f t e x v x t dxdt
exvx dx
sss s s s
ssss
T
ss s s
ss
′
+= =
−−−−−−−−−−−−−−−−−−−−−−−−−
+−+
+= +
+
zz
zz
z
λϕ
λ
ϕ
ϕ
() ( )
() ( () ())(,)
()(,) ()()(,)
()(,)
0
0
0D
DQ
D
T
-интегральное тождество выполняется.
Второй этап.
fxt ftex
xex
Sxt utex
Nss
s
N
Nss
s
N
Nss
s
N
(,) () ()
() ()
(,) () ()
=
=
=
=
=
=
∑
∑
∑
1
1
1
ϕϕ
- решение имеет такой вид.
Третий этап. Доказательство фундаментальности последовательности
Sxt
N
(,). Оценим
модуль:
ut e e f d
ut e f d
e
e
efd
ss
tt
s
t
ss
t
s
t
s
t
s
t
s
s
T
ss
s
s
s
() ( )
() ( )
()
()
≤+
≤+
−
≤
≤+
−−−
−
−
−
z
z
z
ϕττ
ϕττ
ϕ
λ
ττ
λλτ
λ
λ
λ
0
22
2
2
0
2
2
2
0
1
2
2
1
Интегрируем слева и справа:
vtdt
eT
fd Tfd
xt S xt xt S xt dt
s
T
s
t
ss
s
T
s
ss
T
M
HQ
M
HD
T
s
T t
2
0
2
2
2
0
22
0
22
0
2
1
2
1
10 1
() () ()
(,) (,) (,) (,)
,
() ()
z
z
z
z
≤
−
+≤+
F
H
G
I
K
J
−=− =
−
ϕ
λλ
ττ
λ
ϕττ
λ
N > M
SS
NN
www.uchites.ru
60
=≤∇∇=
=≤+
F
H
G
I
K
J
∑
zz
∑
z
z
∑
z
∑
=+
=+ =+
u
s
S=M+1
N
() ( ) ()
()
()
te x dt C u t e edx
CutdtC fdt
s
H
s
T
ss
D
SM
N
T
s
T
s
SM
N
ss
T
SM
N
T
t
1
2
1
2
0
1
0
1
2
0
1
2
22
0
1
D
λϕ
Значит: последовательность фундаментальна и она сходится:
Sxt Uxt
N
HQ
T
(,) (,)
,
()
→
10
Sxt C fdt
Cf
N
HQ
ss
T
s
N
LL
T
Q
T
(,)
,
((
()
10
22
2
2
22
0
1
2
22
≤+
F
H
G
I
K
J
≤
≤+
F
H
I
K
z
∑
=
ϕ
ϕ
D) )
Переходим к пределу:
uC f
HQ L L
TDQ
T
10
22
2
2
22
,
((
()
≤+
F
H
I
K
ϕ
))
Надо доказать, что u - задает решение задачи.
∇∇− = +
z
z
z
S v S v dxdt f vdxdt v x dx
NNt
Q
N
Q
N
T
T
bg
ϕ
(,)0
D
При переходе к пределу выполняется интегральное тождество:
∇∇ − = +
z
z
z
u v uv dxdt fvdxdt v x dx
t
QQ
T
T
bg
ϕ
(,)0
D
Теореме доказана. Из этой теоремы не следует единственность.
UЕдинственность обобщенного решения смешанной задачи для
уравнения теплопроводности
uufxt xtQ
u
tT
T
−= ∈∆ ( , ) , ( )
= ( )
Г
bg
1
02
Теорема.
Задача (1)-(3) может иметь не более одного обобщенного решения.
Доказательство.
Пусть
∃uu
12
, -обобщенные решения, оценим
ω
=
−
uu
12
.
∇∇ − =
z
ωω
v v dxdt
t
Q
T
bg
0 (4)
vx t x d
t
T
(,) (,)=
z
ωθθ
- добавлена гладкость по t.
∃=−vxt
t
ω
(,)
Условия, налагаемые на v:
uu
D
TT
= ; =
Г
00 .
∇=∇
z
vx t x d
t
T
(,) (, )
ωθ
θ
0
2
0
=+∇∇=
z
z
z
z
ωωωθθ
(,) (,) (, )x t dxdt dx x t dt x d
t
TT
ДQ
T
