Лекции - Уравнения в частных производных

www.uchites.ru

41

Au a x

u

x

axu

Au au au

uvw H Q H Q

uAudxfdx

vAvdx

wAwdx

i

n

i

x

i

n

QQ

Q

i

1

0

1

0

11

1

0

=+

=− +

∈∀∈

∇∇ + =

=

+

=

+

∑

zz

z

bg bg

bg

bg bg

di

bg

∂

ϕ

ϕϕ ϕ

ϕϕ

, ,

7

8

9

Теорема 2.

1. Если задача (3) (4) имеет единственное решение, то задача (1) (2) также имеет

единственное решение для

∀∈fLQ

2

bg

.

2. Если задача (3) (4) имеет нетривиальное решение, то задача (1) (2) разрешима тогда и

только тогда, когда

fw

LQ

,

bg

2

0

=

, где w - решение однородной сопряженной задачи.

3. Размерности подпространств в решениях задач (3) (4) и (5) (6) совпадают и конечны.

Задача Неймана:

−= ∈

=∈

∆ ufx xQ

u

n

xQ

Q

bg b g bg

bg bg

1

2

∂

0

Рассмотрим задачу на собственные значения:

−= ∈

=

∈∀∈

∇∇ =

zz

∆ uux xQ

u

n

uHQ vHQ

u v dx u v dx

Q

QQ

λ

∂

λ

∂

bg b g b g

bg

bg bg

bg

10

11

Если то для

выполняется:

12

0

11

, Теор

ема 3.

1. Собственные значения оператора Лапласа с "-" с условиями Неймана вещественные,

конечнократные, неотрицательные и состоят из следующих чисел:

λ

0

00=>→

+

∞

→

∞

и при

s

:,

s

s .

2. Соответствующие собственные функции

u

s

lq

составляют ортонормированный базис в

LQ

2

bg

.

3.

u

s

λ

+

R

S

|

T

|

U

V

|

W

|

1

составляют ортонормированный базис в HQ

1

bg

.

Доказательство.

www.uchites.ru

42

∇∇ + = +

=+

−=+

∇= =

+

=

→→∞

z

zz

u v dx u v dx u v dx

u v Au v

vHQuAu

vu

u dx u dx Au u

QQQ

HQ HQ

QQ

λ

λµ

λ

µ

µλ

1

0

11

1

2

bg

bg b gb g

bg b g

bg bg

,,

,.

:

,

,.

Т . к . произвольная в то :

Возьмем вместо функцию

и :

Если то

Первая часть теоремы доказана.

По Гильберту-Шмидту строится

u

s

lq

- ортогональный базис в HQ

1

bg

и пусть

u

s

LQ

2

1

bg

= .

∇∇ =

∇∇ + = +

zz

u udx uudx

u u u u dx u u dx

s

Q

rss

Q

r

sr sr

Q

ss

Q

r

λ

bgbg

1

u

s

HQ

s

1

2

1

bg

=+⇒

+

R

S

|

T

|

U

V

|

W

|

λ

- ортонормированный базис в HQ

1

bg

.

Теорема 3 доказана.

Задача Дирихле - однозначная разрешимость.

Теорема 4 о гладкости решения задачи Неймана.

Пусть

fLQ HQ

loc

k

∈∩

2

bg bg

- правая часть уравнения. Пусть uHQ∈

1

bg

-

обобщенное решение задачи (1) (2), тогда:

uH Q

loc

k

∈

+

2

bg

Доказательство - аналогично теореме 3.

Теорема 5.

Пусть граница

∂

QC

k

∈

+ 2

; пусть правая часть fHQ

k

∈

bg

. uHQ∈

1

bg

-

обобщенное решение задачи (1) (2), тогда:

uH Q

k

∈

+

2

bg

.

Теорема 6.

Пусть граница

∂

QC

∈

2

; правая часть - fLQ

∈

2

bg

; uHQ

∈

1

bg

- обобщенное

решение задачи (1) (2), тогда:

uHQ

u

n

Q

∈=

2

0

bg

∂

.

Доказательство.

Обобщенное решение:

∇∇ =

z

u v dx f v dx

QQ

для

∀

∈

vHQ

1

bg

.

−+ =

z

∆ uv dx

u

n

vds fvdx

QQ

Q

∂

Уравнение (1) выполняется почти всюду в Q , и:

www.uchites.ru

43

∂

u

n

vds

u

n

Q

z

=⇒ =00

UМетод Ритца

Суть: сведение бесконечномерного случая к конечномерному.

Рассмотрим:

Eu u lu

HQ

bg bg

bg

=+

2

1

2 , где:

l(u) - линейный, ограниченный функционал в

′

⊂HHQ

1

bg

.

Найдем минимум квадратичного функционала:

Eu u l u l l u l l l

HH H

bg d i

≥− +−= −−≥−

′′ ′

222

2

22

2.

∃=

∈

′

inf

u

H

Eu d

bg

- конечное число.

Найдется v

m

lq

=

∞

1

такая, что: lim ,

m

mm

Ev d v

→∞

=

bg

lq

- минимизирующая

последовательность.

∃∈

′

u

H

, такой, что: E(u)=d . u - минимизирующий элемент.

Теорема 1.

Существует единственный

u

H

∈

′

, минимизирующий функционал E . При этом этом любая

минимизирующая последовательность является сходящейся к элементу u :

vu

m

→ .

Доказательство.

Возьмем любую минимизирующую последовательность. Очевидно:

vv

vvvv

mk

H

mkmk

H

±

=+±

′

2

1

4

1

4

1

2

22

,

bg

Почленно сложим соотношения с "+" и с "-":

vv

Ev Ev E

vv

dd

mk

H

m

H

k

H

mk

H

mk

−

=+−

+

=

=+−

+

F

H

G

I

K

J

≤+−=

′

′′

′

2

1

2

1

22

1

22

2

22

2

bg bg

ch

εε

Доказано: последовательность

v

m

lq

- фундаментальная в полном пространстве, значит:

vuH

m

→

′

в и, значит :

v u lv lu Ev Eu Eu d

m

H

mm

′

→→ →=,, ,

b g bg b g bg bg

.

Доказано: если

v

m

lq

- минимизирующая последовательность, то она сходится к

минимальному элементу.

Доказательство единственности от противного: пусть есть второй минимальный элемент;

составим минимизирующую последовательность:

uuuu

1212

,,,,L .

Она не сходится, значит, второй минимальный элемент не существует.

Пусть

ϕ

12

,,,,LL

s

H∈

′

составляют линейно независимую систему функций, линейная

оболочка которой плотна в

′

H

, т.е. полная система, значит:

∀∈

′

u

H

может быть аппроксимирован

ϕ

s

lq

.

Обозначим через

RH

k

⊂

′

- конечномерное подпространство

′

H

, натянутое на первые

k функций

ϕ

12

,,,L

k

.

Рассмотрим

inf

uR

k

Eu

∈

bg

- задача сводится к конечномерной.

www.uchites.ru

44

uc

i

k

i

=

∑

1

ϕ

, и E(.) может быть представлен в виде функции k переменных; обозначим её:

Fc c Ec c c

cc cl

kkk

ij

H

ij i i

i

k

ij

k

11122

11

2

,,

,

LL

bgb g

di bg

=++

+

=

=+

′

==

∑∑

ϕ

ϕϕ ϕ

Необходимое условие экстремума:

∂

F

c

ik

i

==012, , ,..., , тогда:

ϕϕ ϕ

ij

H

ji

i

k

ij

k

cl,

,

di bg

′

==

+=

∑∑

20

11

, где i=1,...,k. (1)

Система алгебраических уравнений (1) имеет единственное решение, т.к. её определитель

(Грама) отличен от 0.

ϕϕ ξξ ξϕ

ij

H

jj

ij

k

ii

i

k

H

,

di

′

==

′

∑∑

=>

11

2

0

Обозначим решение

cc

k

1

,,L , и: v c Ev Ev

ki

k

i

k

=≥≥

=

∑

ϕ

1

12

,

bg bg

L - монотонно

невозрастающая последовательность минимальных значений функционала.

v

k

lq

- последовательность Ритца.

Теорема 2.

Последовательность Ритца является минимизирующей, и, следовательно, сходится к

минимизирующему элементу u :

vuk

k

→→

∞

,

.

Доказательство.

Т.к.

L

k

ϕ

1

,,L

bg

всюду плотна в

′

H

, то:

∀

>

∃

∈

ε

0 и kvR

k

, такие что:

uv

H

−<

′

ε

.

Рассмотрим значение

Ev

ε

bg

:

Ev v lv v uu lv uu

vu vuu u lvu lu

duldc

H

εε εε ε

εε ε

εε ε ε

bg bg b g

bg bgbg

=+ =−++−+=

=−+ − + + −+ ≤

≤+ + + =+

′

22

2

1

22

222

22

,

Таким образом: Ev d c

ε

bg

≤

+

1

, и при :

s k Ev Ev d c

sk

≥≤

≤

+

bg bg

1

ε

.

Теорема 3.

u

H

∈

′

является мимимизирующим элементом для функционала E(u) тогда и только

тогда, когда

uv lv v H

H

,

bg bg

′

+=

∀

∈

′

0 , ( 2 )

Доказательство.

Необходимость: пусть u - минимизирующий элемент; возьмем

∀∈

′

∀

∈v

H

t

R

и , то: Eu tv Eu

+

≥

bgbg

, т.к. u -

минимизирующий. Обозначим через

Fu Eu tv

bg b g

=

+

. Необходимое условие

экстремума:

dF

dt

t =

=

0

0 .

F t u u v t t v l u tl v

H

bg b g bg bg

=+ + ++

′

2

222,.

www.uchites.ru

45

dF

dt

uv lv

t

H

=

′

=⇒ + =

0

00,,

bg bg

что и требовалось доказать.

Достаточность: пусть выполняется (2), то рассмотрим:

Eu v u uv v lu lv Eu

H

+= + + + + ≥

′

b g b g bg bg bg

22

222, ,

т.е.

Eu v Eu+≥ ⇒

bgbg

u - минимизирующий элемент, что и требовалось доказать.

Выводы.

1. Существует единственный минимизирующий элемент - предел минимизирующей

последовательности ( последовательности Ритца).

2. Минимизация функционала связана с обобщенным решением краевой задачи.

3. Метод Ритца можно использовать для решения эллиптической задачи.

Eu u lu

H

bg bg

=+

′

2

uv lv v H

H

,

bg bg b g bg

′

+=

∀

∈

′

02

Примеры.

1.

′

=HHQ

&

1

bg

Eu u fu f L Q

LQ

bg b g b g

bg

=∇ − ∈

2

2, ,

E u u dx fudx

QQ

bg bg

=∇ −

z

2

23

∇∇ − =

z

u v dx fudx

QQ

0 - интегральное тождество ( 4 )

(4) определяет обобщенное решение задачи Дирихле для уравнения Пуассона.

−=

∈

=

∆ ufx xQ

u

Q

bg b g bg

bg

5

6

∂

0

Теорема 4.

1. Существует единственный

uHQ∈

&

1

bg

, минимизирующий функционал в

&

HQ

1

bg

;

∀ vHQ

m

lq

bg

&

1

- минимизирующая последовательность

⇒→∈vuHQ

m

&

1

bg

2. Последовательность Ритца для функционала (3) в

&

HQ

1

bg

является минимизирующей.

3.

uHQ∈

&

1

bg

является минимизирующей для функционала (3) тогда и только тогда,

когда u является обобщенным решением задачи (5)-(6).

2. Задача Неймана.

Любое решение такой задачи равно сумме частного неоднородного и общего однородного

решения. Будем искать решение из

uHQ

∈

%

1

bg

, где

%

:HQ u HQ udx

Q

11

0

bg bg

=∈ =

R

S

|

T

|

U

V

|

W

|

z

- замкнутое подпространство

пространства

HQ

1

bg

.

Обобщенное решение задачи (7)-(8) :

∇∇ =

z

u vdx fvdx

QQ

9

bg

www.uchites.ru

46

Если u=v=const, то илевая и правая части не изменятся и: fdx

Q

=

z

0 .

Решение существует и единственно.

u v u vdx

E u u fvdx

HQ

Q

LQ

Q

,

%

|

bg

bg b g

bg

′

=∇∇

=∇ −

z

2

2 10

Будем полагать :

′

=HHQ

%

1

bg

, тогда:

Теорема 5.

1. Существует единственный

uHQ∈

%

1

bg

, минимизирующий функционал в

%

HQ

1

bg

;

∀ vHQ

m

lq

bg

%

1

- минимизирующая последовательность ⇒→∈vuHQ

m

%

1

bg

2. Последовательность Ритца для функционала (10) в

%

HQ

1

bg

является

минимизирующей.

3.

uHQ∈

%

1

bg

является минимизирующей для функционала (10) тогда и только тогда,

когда u является обобщенным решением задачи (7)-(8).

UИзучение классических решений эллиптических задач.

§1. Формула Грина.

QR

n

⊂ - ограниченная область;

∂

QCuvCQ∈∈

12

;,

ch

∆ uvdx

u

n

vds u vdx

QQQ

=−∇∇

z

∂

∆ vudx

v

n

uds u vdx

QQQ

=−∇∇

z

∂

Вычтем из первого второе:

∆∆uv vu dx

u

n

v

n

uds

QQ

−= −

F

H

G

I

K

J

zz

bg bg

∂

1

UИнтегральное представление производной

Определение.

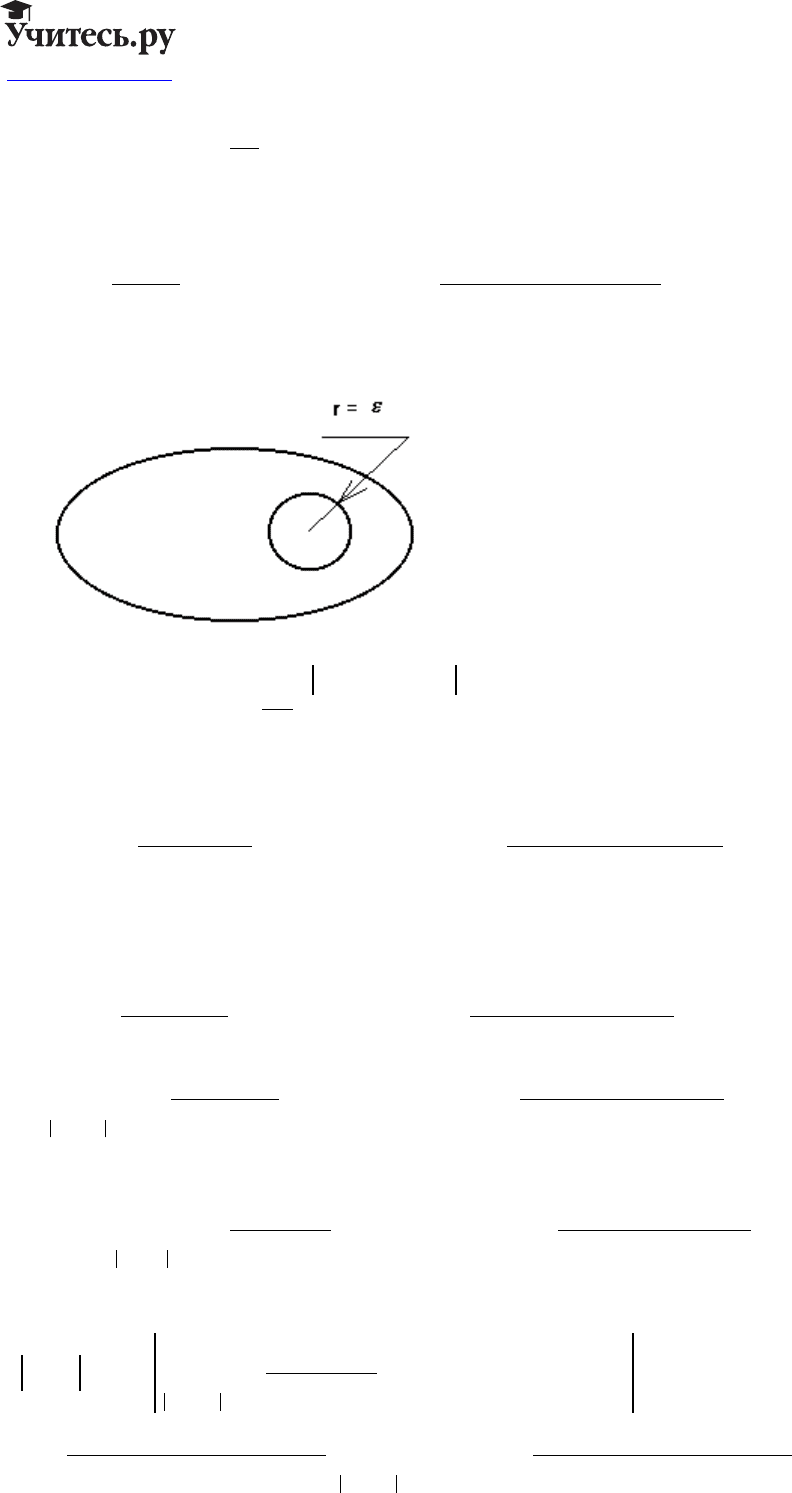
Фундаментальное решение уравнения Лапласа:

U

x

nx

n

x

n

bg

=

−

≥

−=

R

S

|

T

|

−

1

2

3

1

2

1

2

σ

π

,

ln ,

Следствие.

∆ Ux x

bg

=≠00,

Теорема 1.

www.uchites.ru

47

Пусть QR

n

⊂ - ограниченная область с границей класса

C

1

.

Пусть

fCQ∈

2

ch

, тогда:

fx f U x d

f

n

Ux

n

fds

Q

bg bgb g

bg

=−−

−−−

−

z

∆

ξξξ

∂

ξ

∂ξ

∂

ξ

∂

ξ

()

Доказательство.

Рассмотрим:

-- область без шара.

Sx x

QSx

r

rr

bg

mr

bg

=−<

=

ξξε

:

\Ω

∆∆

Ω

fUx Ux f d

f

n

Ux

n

fds

r

ξξ ξξξ

∂ξ

∂

ξ

∂ξ

∂

ξ

ξξ

ξ

∂

bg b g b g bgdi

bg

−− − =

=−−

−

L

N

M

O

Q

P

z

∆

Ω

fUx d

f

n

Ux

n

fds

f

n

Ux

n

fds

r

Q

x

ξξξ

∂ξ

∂

ξ

∂ξ

∂

ξ

∂ξ

∂

ξ

∂ξ

∂

ξ

ξξ

ξ

ξξ

ξ

ξε

bg b g

bg

−=

=−−

−

L

N

M

O

Q

P

+

+−−

−

L

N

M

O

Q

P

z

−<

Обозначим :

I

f

n

Ux

n

fds

x

ε

ξξ

ξ

ξε

∂ξ

∂

ξ

∂ξ

∂

ξ

=−−

−

L

N

M

O

Q

P

−<

z

bg

Надо доказать, что :

Ifx

ε

→→

bg

, при 0.

Обозначим :

I

f

n

Ux ds

M

n

ds

M

n

x

n

x

n

ε

ξ

ξε

ξ

ξε

∂ξ

∂

ξ

σε

1

22

0

2

1

2

=−≤

≤

−

=

−

→

−<

−

−<

−

z

bg

bg bg

www.uchites.ru

48

где :

σ

n

- площадь поверхности единичной сферы в n-мерном пространстве.

Учитывая, что:

∆ Ux x

Ux

n

Ux

dx

x

n

bg b g

bg bg

=

≠

−

=−

−

=

−=

−

00

1

∂ξ

∂

∂ξ

ξσε

ξ

ξε

I

Ux

n

fds

fds fx f fxds

x

n

xx

ε

ξ

ξε

ξ

ξε

ξ

ξε

∂ξ

∂

ξ

σε

ξξ

2

1

=

−

≤

≤=+−

−<

−

−< −<

z

zz

bg

bg bg bg bgch

Обозначим :

Iffxds

x

ε ξ

ξε

ξ

3

=−

−<

z

bg bgch

I

C

ds

C

n

x

n

εε

ξε

ε

σε

ε

σε

σε ε ε

3

1

00≤=≤→→

−

−=

−

z

,

Первая теорема о среднем.

Определение.

Функция u называется гармонической в области Q, если она удовлетворяет в этой области

уравнению Лапласа.

Пусть u(x) - гармоническая в

Ω⊂

R

n

.

D- ограниченная область

∂

Ω⊂

C

1

.

uC

u

n

ds

udx

Q

n

ds u dx

Q

QQQ

∈⇒ =

⇒⋅= =∇∇

z

zzz

2

0

11

Ω

∆

ch

bg

∂

1

Теорема 1.

Пусть

fx C Q

bg bg

∈

2

- гармоническая функция в Q , и пусть:

Sx Q

r

bg

⊂ , тогда : fx

r

fds

n

xr

bg bg bg

=

−

−=

z

1

σ

ξ

2

Значение гармонической функции в центре сферы равно среднему арифметическому её

значений на границе сферы.

Доказательство.

u x const

bg

≠

Обозначим :

I

ux

n

fds

I

fx

n

ux ds

xr

1

2

=

−

=−

−=

z

∂

ξ

∂

ξ

∂

ξ

bg

I

nr

f

n

ds

n

xr

2

1

2

0

=

−

=

−

−=

z

σ

∂ξ

∂

ξ

bg

www.uchites.ru

49

I

r

fds

n

xr

1

=

−

−=

z

σ

ξ

bg

Вторая теорема о среднем.

Пусть fx C Q

bg bg

∈

2

- гармоническая в Q функция;

Sx Q

r

bg

⊂ , тогда : fx

n

r

fd

n

xr

bg bg

=

−<

z

σ

ξξ

ξ

Доказательство.

fx f ds

n

x

bg bg

=

−

−=

z

1

σρ

ξ

ξρ

fx f ds

n

x

bg bg

σρ ξ

ξ

ξρ

−

−=

=

z

1

fx r

n

dfds fd

n

r

xxr

bg

bg bg

σ

ρξ ξξ

ξ

ξρ ξ

==

zz z

−= −<1

fx

n

r

fd

n

xr

bg bg

=

−<

z

σ

ξξ

ξ

, что и требовалось доказать.

UПринцип максимума

Теорема.

QR

n

⊂ - ограниченная, связная;

u(x) - гармоническая в Q, непрерывная в

Q , u x const

bg

≠

, тогда:

min ( ) ( ) max ( )

xQ xQ

ux ux ux

∈∈

<

′

<

∂∂

Доказательство.

Предположим противное:

Muy ux

xQ

=

∈

( ) max ( ) , yQ

∈

.

Тогда докажем, что в произвольной точке области значение функции U совпадает с M ,т.е. u-

const. Возьмем

∀∈zQ и соединим ломанной l точки Y и Z . Покроем ломанную конечным

числом шаров:

lSx

r

j

n

=

()

1

U

. Шары такие : Sx Q

r

j

()⊂ и xSx

j

∈

−

()

1

, причем:

xy

1

= ,

x

z

J

= .

uy ux

n

r

ud

n

xr

() ( ) ()==

−<

z

1

σ

ξξ

ξ

n

r

uy u d

n

xr

σ

ξξ

ξ

bg bg

ch

−=

−<

z

0

Если

uy u() ()−≥

ξ

0 ,то: uY u() ()

−

≡

ξ

0 , yr

−

<

ξ

ux uy M() ()

2

==

ux ux M() ()

32

==

L

uz

M

()=

Теорема доказана.

www.uchites.ru

50

UЕдинственность классического решения задачи Дирихле для уравнения

Пуассона

−=∆u

x

f

x

() () ()

x

Q

∈

(1)

ux

Q

∂

ϕ

= () ()

x

Q

∈

∂

(2)

fCQ CQ∈∈

ch b g

,

ϕ∂

- это не гарантирует существование решения. uCQ CQ∈

∩

2

() ( )

Теорема.

Задача (1) (2) может иметь не более одного классического решения.

Доказательство.

Предположим противное: пусть есть два классических решения:

uu

12

и . Это значит:

−=∆ux fx

1

() () ()

x

Q∈ (3)

ux x

1

() ()=

ϕ

()

x

Q∈

∂

(4)

−=∆ux fx

2

() () ()

x

Q∈ (5)

ux x

2

() ()=

ϕ

()

x

Q∈

∂

(6)

−=∆

ω

()

x

0 ()

x

Q∈ (7)

ω

()

x

= 0 ()

x

Q

∈

∂

(8)

ω

=−uu

12

Значит:

ω

= 0 и uu

12

=

Следовательно, если существуют два решения, то они равны друг другу. Что и требовалось

доказать.

UОбобщенные решения смешаной задачи для волнового уравнения

uufxt

tt

−=∆ (,) (,)xt Q

T

∈

(1)

u

T

Г

= 0 (2)

ux

t =

=

0

ϕ

() (

x

D

∈

) (3)

∂

ψ

u

t

x

t =

=

0

() (

x

D

∈

) (4)

D

R

n

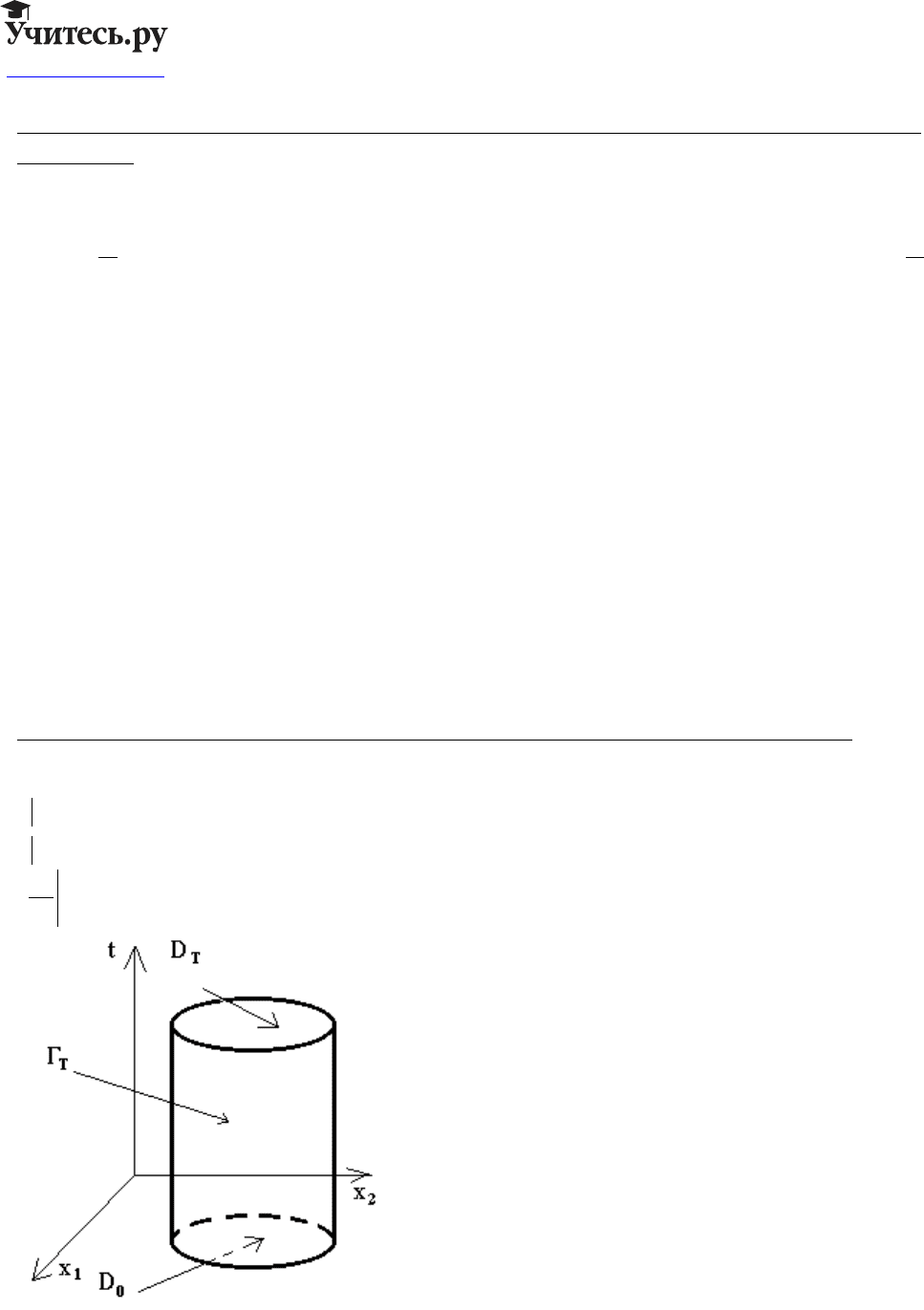
⊂ QD T

T

=

×

(, )0

Обозначения:

DDt

t

=×

lq

; Г

T

QT

=

×

∂

0,

bg

.

fLQ

T

∈

2

()

ϕ

ψ

,(∈ LD

2

)

Лекции - Уравнения в частных производных

Подождите немного. Документ загружается.