Лекции - Уравнения в частных производных
Подождите немного. Документ загружается.


www.uchites.ru
11
χ
Ω
Ω
Ω
()
,
,
x
x
x
=
∈
∉
R
S
T
1
0
Рассмотрим
ξ
δ
()x - финитная, бесконечно дифференцируема в
Ω
.
01
1
0
2
≤≤
≡∈
≡∈
ξ
ξ
ξ
δ
δδ
δδ
() ;
() , ;
() , .
x
xx
xx
Ω
Ω
Значит,
supp
ξ
δ
()xQ⊂ .
χξ χξ
χξ χξ χξ µ
δδ
δδ δδ
δδ
ΩΩ
Ω
Ω
Ω
Ω
Ω
ΩΩ
ΩΩ
() () () ()
() () () () () () ( \ )
()
\ \
xx xxdx
xxdx xxdx xxdx
LQ
Q
Q
n
−=−=
=− +− +− ≤ →
z
zzz
2
22
2
0
22
0
124444 34444
Аппроксимация получена.
Теорема 2.
Множество непрерывных функций всюду плотно в пространстве
LQ
2
().
Определение 2.
Пусть
fLQ∈
2
() и считается продолженной нулем вне Q (() , )
f
x
x
Q
≡
∉0 . Скажем:
f - непрерывна в среднеквадратичном, если
∀
>
∃
>
ε
δ
00:
fx fx z dx z
Q
() ( ) ,−+ <∀<
z
2
ε
δ
.
Теорема 3.
Любая функция из
LQ
2
() непрерывна в среднеквадратичном.
Доказательство.
Пусть
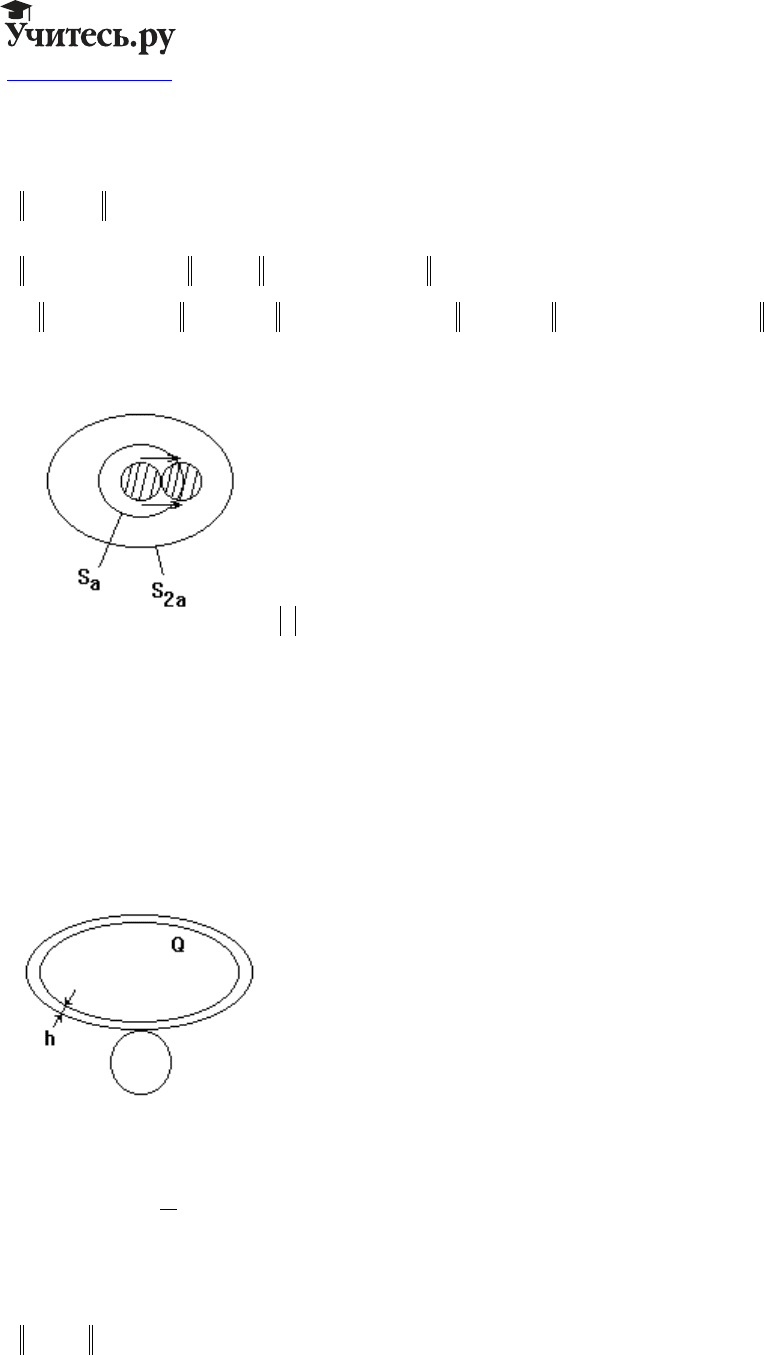
QS
a
⊂ ()0 . Пусть
Fx
xQ
xS Q
a
()
,;
,()\.
=
∈
∈
R
S
T
1
00
3
lq
www.uchites.ru
12
Fx C S
Fx S
FF
a
a
LS
a
ε
ε
ε
ε
()
&
(())
() ()
(())
∈
⊂
−<
∞
3
0
0
0
2
supp
Оценим:
fx fx z Fx Fx z
Fx Fx Fx Fx z Fx z Fx z
LQ LS
LS LS LS
a
aa a
()() ()()
()() ()() ()()
() ( ())
(()) (()) (())
−+
≤
−
+
≤
≤− + −+ ++−+ <
<< <
222
22 22 22
0
00 0
3
ε
ε
εε
ε
ε
ε
ε
12444434444 1 24444 34444 1 244444 344444
При сдвиге supp сдвигается в пределах шара радиуса 2a.
za<
Теорема доказана.
Определение 3.
fLQfx xQ
f x f y x y dy h
fx fy x ydy
hh
Q
hh
R
n
∈≡∉
=− >
=−
z
z
2
0
0
() ,
() () ( )
() () ( )
(2)
(3)
()
ω
ω
fx
h
() - бесконечно дифференцируема, финитна.
Свойства:
fx C R
fx xQ h
h
n
h
()
&
()
() ,(, ) .
∈
≡>
∞
0
ρ
fx
h
() - осреднение функции f.
Теорема 4.
ff h
h
LQ
−→→
2
00
()
,.
Любая функция из
L
2
сколь угодно точно аппроксимируема своими осреднениями -
бесконечно дифференцируемыми, финитными в
R
n
.
Доказательство.
www.uchites.ru
13
f x fx fy x ydy fx
hh
Q
() () () ( ) ()−= −−=
z
2
2
ω
От Q к
R
n
, от
R
n
к Sx
h
()
=−−⋅−=−⋅−≤
≤−⋅−≤⋅−
−≤ − =
=+
−=−
−=
=
=
−< −< −<
−< −< −<
−<
zzz
zz z
zzz
f y x y dy f x x y dy f y f x x y dy
fx fy x ydy
C
h
fx fy dy
fx fxdx
C
h
dx f x f y dy
yxz
xy z
xy z
C
h
h
xyh
h
xyh
h
xyh
xyh
h
xyh
n
xyh
h
Q
n
Qxyh
()() () () (()())()
() () ( ) () ()
() () () ()
ωω ω
ω
22
2
2
2
n
Qzh
n
z
n
n
dx fx fx z dz
C
h
dz fx fx z dx
C
h
hC
zz zz
−+ = −+ =
==⋅
<<
<
() ( ) () ( )
.
2
1
2
Ω
ε
εε
124444 34444
При
h →→
z
00, .
Возьмем любые две функции:
fCQ
CQ
D f dx f D dx
QQ
∈
∈
⋅=− ⋅
zz
α
α
α
α
α
ϕ
ϕϕ
()
&
()
()1
Определение.
LQ uL Q
loc
22
() (), :=∈ ∀ ⊂ΩΩΩ
o
t
- множество функций, принадлежащих L
2
на любом
компакте внутри области.
u
x
L
uL
=∉
∈−
1
01
1
2
2
(,)
(, )
εε
Определение 1.
Пусть
fL Q
loc
∈
2
()
fLQ
loc
α
∈
2
() - обобщённая производная функции f, если ∀∈
ϕ
α
&
()CQ выполняется:
fD dx f dx
QQ
α
α
α
ϕϕ
z
z
=−()1 (1)
Теорема 1.
Обобщённая производная определяется единственным образом.
Доказательство.
Предположим противное:
∃ff
12
α
α
, - обобщённые производные функции f.
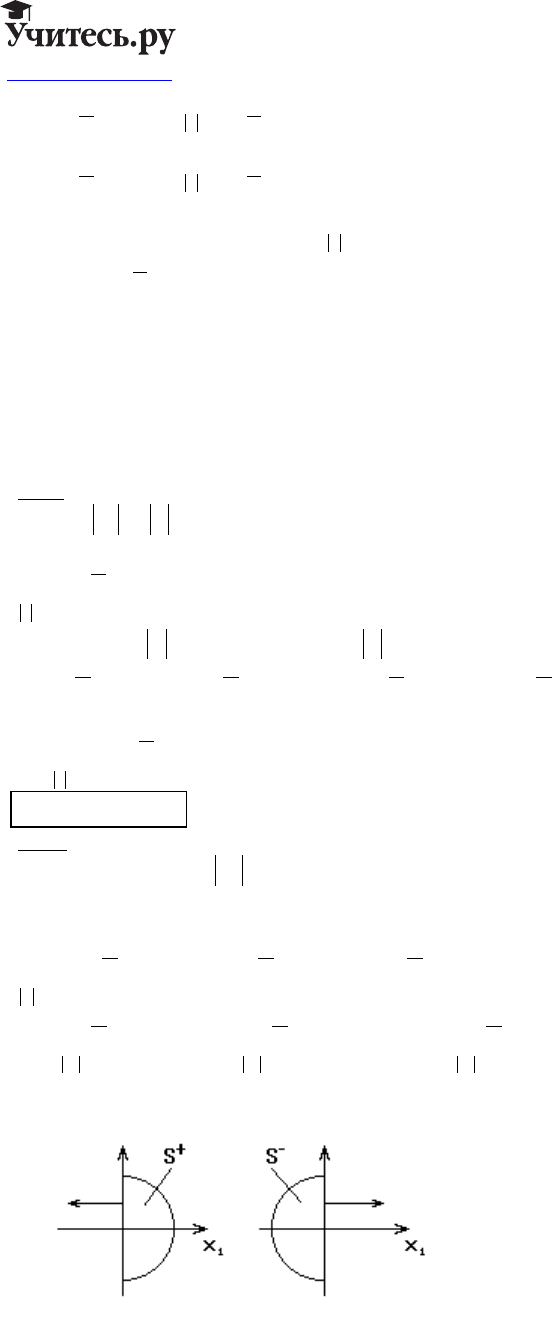
www.uchites.ru
14
fD dx f dx
QQ
α
α
α
ϕϕ
z
z
=−()1
1
(2)
fD dx f dx
QQ
α
α
α
ϕϕ
z
z
=−()1
2
(3)
(2),(3) - тождество для
∀∈
ϕ
α
&
()CQ
()ffdx ff
Q
12 12
00
αα αα
ϕ
−=⇒−=
z
- что и требовалось доказать.
Теорема 2.
Обобщённые производные не зависят от порядка дифференцирования.
Доказательство - из интегрального тождества (1).
Примеры обобщённых производных.
UEx 1.U
fx x x() ,=<
1
1
По определению:
fx xdx
x
x
() ()
ϕ
1
1
=
<
z
Пусть
Sxx
+
=<>10
1
:
mr
и Sxx
−
=< <10
1
:
mr
=−=−⋅+⋅=
=−
+− +−
z
z
z
z
z
<
x x dx x x dx x dx x dx
xxdx
x
S
x
S
x
S
x
S
x
x
11
1
1
11 11
1
11
ϕϕ ϕϕ
ϕ
() () () ()
sign ( )
fx
x
1
1
= sign
UEx 2.U
fx x x
bg
=<sign ,
11
1
Покажем, что обобщённой производной не существует.
Пусть
∃f
x
1
, то:
f x x dx x dx x dx
xdx xdx xdx
x
x
x
S
x
S
xx x
() () () ()
(, ) (, ) (, )
ϕϕϕ
ϕϕ ϕ
111
1
11 1
0020
<
′
<
′
<
′
<
z
z
z
zz z
=−=
=−
′′
−
′′
=−
′′
+−
где
′
=xx x
n
( ,..., )
2
1) пусть
ϕ
∈
∞+
&
()CS носитель в
S
+
, то :

www.uchites.ru
15
fx xdx
fx xdx
fx x S
x
x
x
x
x
() ()
()()
() ,
ϕ
ϕ
1
1
1
1
1
0
0
0
<
<
+
z
z
=
−=
≡∈
2) пусть
ϕ
∈
∞−
&
()CS : fx xdx
xx
S
11
0() ()
ϕ
−
z
= , значит:
fx xS
x
1
0() ,=∈
−
Вывод:
fx
x
1
0()≡ .
fx xdx xdx
x
xx
1
11
20()() (, )
ϕϕ
<
′
<
z
z
=
′′
Вывод:
f
x
x
( ) sign= , не имеет обобщённой производной.
Теорема 3.
Пусть
fLQ∈
2
() имеет обобщённую производную Df LQ
α
∈
2
(), то:
1.
Dfx Df x x Q
hh
α
α
() ( )();=∀∈ (4)
Df Df h
h
L
αα
−→→
2
00
()
,,
Ω
если
Ω∈Q .
2. Если к тому же
supp
f
Q⊂⇒
⇒= ∈( )() ( )();Df x Df x x Q
hh
α
α
(6)
Df Df h
h
LQ
αα
−→→
2
00
()
, (7)
Доказательство.
( )() ()() () ()
() () ( )
Df x D fy x ydy fyD x ydy
fyD x ydy
hx h
Q
xh
Q
yh
Q
αα α
α
α
ωω
ω
=−=−=
=− − =
zz
z
1
Выберем h так, чтобы Sx Q
h
()⊂
=− − =
−=−
→→
z
() () ( ) ( )().
()
,
() ()
1
00
2
22
α
αα
αα α α
α
ω
Dfy x ydy Df x
Df Df Df Df
Df h
yh
Q
h
h
L
h
L
ΩΩ
Подсказка: если функция финитна, то её носитель - внутри области.
Если функцию умножить на срезающую, то ничего не изменится.
Теорема 4.
f L Q const f i n
x
i
∈≡⇔==
2
01( ) , ,..., .
Утверждение.
www.uchites.ru
16
Пусть ∃=∀=fin
x
i
01, ,..., , то f L Q const∈
≡
2
()
fx f x
xxh
ii
() ( )()=⇒
=
00
Пусть
x
Q∈ - открытый компакт, то ()()fx
hx
i
=
0 для
x
∈
Ω
ff h
ff hh
CCdx CC
h
L
hh
L
hh hh
−→→
−→→
−
R
S
T
U
V
W
=−
z
2
12
2
12 12
00
00
12
2
12
()
()
,
,,
.
Ω
Ω
Ω
µ
nh
h
C
C
Cfx Cx
()
() , .
Ω
Ω
lq lq
12
0→⇒
→≡∀∈
- фундаментальна.
Теорема 5.
Пусть
QQ Q=∪
12
. fLQ
∈
2
() имеет обобщённые производные () ()Df LQ
Q
α
1
21
∈ и
() ()Df LQ
Q
α
2
22
∈ , то
существует обобщённая производная
() ()Df LQ
Q
α
∈
2
.
UПространство Соболева
Определение.
fLQ∈
2
()
lq
, такая, что ∃∈
≤
Df LQ k
α
α
2
(), называется пространством Соболева порядка
k.
fLQ DfLQ k HQ
k
∈∃∈ ≤=
22
(): (), ()
α
α
n
s
Обозначения:
HQ
k
bg
, WQ
r
k
() или WQ
k
().
Введём
(,)
()
uv DuDvdx
HQ
Q
k
k
=
z
∑
≤
αα
α
.
Утверждение.
HQ
k
() - гильбертово(унитарное, сепарабельное).
Теорема 1.
HQ
k
() - полное пространство.
Доказательство.
u
n
lq
- фундаментальная в HQ
k
()⇒ uu nm
nm
HQ
k
−→→∞
()
;,
2
0
Du Du dx nm
nm
Q
k
αα
α
−→→∞
z
∑
≤
2
0; ,
.
α
- мультииндекс
α
- может быть равен 0.
Du Du dx nm
nm
Q
αα
−→→+∞
z
2
0; ,
uu
n
→
0
в LQ
2
().
Du u
n
α
α
→ в LQ
2
().
Интегральное тождество для
u
n
:

www.uchites.ru
17
D u dx u D dx C Q
n
Q
n
Q
k
α
α
α
ϕϕϕ
⋅=− ∀∈
z
z
() ,
&
()1
Из сильной сходимости следует слабая:
udx uD dx u Du
QQ
α
α
α
α
α
ϕϕ
z
z
=− ⇒ =()1
00
u u dx n
Du Du dx n
Du Du dx n
n
Q
n
Q
n
Q
k
−→→∞
−→→∞
−→→∞
z
z
z
∑
≤
0
2
0
2
0
2
0
0
0
;
;
;
αα
αα
α
Вывод: пространство полное.
Свойства пространств Соболева.
1.
uHQ uHQ
kk
∈⇒∈
′
() ( ) для
′
⊂QQ
.
2.Если
uHQaCQ
kk
∈∈(), ( ), то au H Q
k
∈
().
3.Если
uHQi QQ Q
k
i
∈==∪(); ,;12
12
, то uHQ
k
∈
().
4.Если
uHQ
k
∈ (), то
ff h R Q
h
H
n
k
−→→∀⊂⊂
()
,( :)
Ω
Ω
Ω
0 0
если
supp
f
Q⊂ , то ff h
h
HQ
k
−→→
()
,00.
5.
ω
- невырожденное, k раз непрерывно дифференцируемое преобразование, отображающее
Q
ε
в Ω
ε
.
ω
ε
ε
: Q →Ω и пусть QQ⊂⊂
ε
ε
, Ω
Ω
.
Пусть
ω
()Q =Ω.
Пусть
fy H
k
() ( )∈Ω, то fxHQ
k
(()) ()
ω
∈ .
Утверждение.
Невырожденная, гладкая замена переменных сохраняет принадлежность функции
пространству Соболева.
6.Обозначим
KxRxa
a
n
=∈ <:
n
s
- куб со стороной 2a с центром в начале координат.
Множество бесконечно дифференцируемых функций замыкания куба является всюду
плотным в
HK
k
a
().
C
KHK
a
k
a
∞
=() ().
Доказательство.
Раздвинем область, возьмём
∀∈fHK
k
a
() и будем её аппроксимировать
последовательностью бесконечно гладких функций.
www.uchites.ru
18
ff
x
σ
σ
σ
=
F
H
G
I
K
J
>,1
(определена в растянутом кубе)
fHK
fCK
k
a
ha
σσ
σσ
∈
∈
∞
()
()
Оценим:
ff ff f f
h
HK HK
h
HK
h
k
a
k
a
k
a
−≤−
+
−
→→
σσσσ
() () ()
, 0 0
1244 344
Df Df
LK
a
αα
σ
−≤
2
()
Выберем
∀>
ε
0 и рассмотрим
ϕ
α
∈ CK
a
()
≤ − +− +− ≤
≤+ −
F
H
G
I
K
J
+
F
H
G
I
K
J
−
F
H
G
I
K
J
≤
≤+
F
H
G
I
K
J
−
F
H
G
I
K
J
+−
F
H
G
I
K
J
F
H
G
I
K
J
≤
≤
<
Df Df
x
xx
Df
x
x
Df
x
Df
x
LK LK LK
LK LK
LK
LK
aa a
aa
a
a
αα
εϕ
α
σ
α
σ
αα
σ
αα α
α
α
αα
α
α
ϕϕϕϕ
εϕ ϕ
σ
ϕ
σ
σ
σ
εϕ
σσ
σ
σ
22 2
22
2
2
1
21
1
() () ()
() ()
()
()
() ( )
() ()
из выбора
1244 344
21
1
21
1
2
22
22
1
εϕ σ σ
σ
εεσ σ
σ
ε
σ
σ
αα
ε
α
α
+− ⋅+−
F
H
G
I
K
J
⋅=
=+⋅ +⋅ −
F
H
G
I
K
J
≤⋅
=
=
<
() ( )()
.
()
yDfy C
CC
y
x
dx dy
LK
nn
nn
n
a
124444 34444
UРазбиение единицы
Теорема.
Пусть
QR
n
⊂ - ограниченная область, пусть QU⊂
α
α
U
- покрытие замыкания Q,
α
- может
равняться бесконечности.
U
α
- открытые, тогда: существует конечный набор
ϕ
j
jJ
n
s
( ,..., )=1 - финитные, бесконечно
дифференцируемые в
R
n
, неотрицательные функции, такие, что:
11
21
3
1
1
)();
)();( );
) : sup
ϕ
ϕ
αϕ
α
j
j
J
j
j
J
j
x
xxQ
jU
=
=
∑
∑
≤
≡∈
∀∃ ⊂
Используется для локализации свойства: U имеет свойство на
D
R
n
⊂ , расширяем D на
R
n
путём домножения на
ϕ
j
j
J
=
∑
1
.
Доказательство.

www.uchites.ru
19
Возьмём ∀∈yQ. Для ∀∃=
∈
yyyU
α
α
α
(): - y покрывается множеством U
α
.
Для каждой выбранной y построим:
%
()
&
();
$
()
%
( ) sup
$
,
$
()
(())
fx C R fx
fy f U
NxRfx
NU y
y
n
y
yy
y
n
y
y
∈≤≤
=⊂
=∈ >
⊂=
∞
01
1
0
α
α
αα
{}
Q покрывается NQ N
yy
y
: ⊂
U
. Из бесконечного покрытия выберем конечное
подпокрытие:
QN
yj
j
N
⊂
=1
U
.
Обозначим:
$
() ()fx fx
yj
j
=
∆
. Обозначим: GN
yj
j
J
=
=1
U
.
Определим:
gx C R
n
()
&
()∈
∞
:
10 1
21
3
)();
)() ;
).
≤≤
≡∈
⊂
g
x
gx x Q
gG
при
supp
Получили:
ϕ
j
j
j
j
J
x
fx
gx f x
()
()
() ()
=
−+
=
∑
1
1
.
Если
fx
j
j
J
()
=
∑
=
1
0, то
x
G∉ ,
g
x
()= 0, и 11
−
=
g
x
() .
Знаменатель в 0 не обращается.
Построена
ϕ
ϕ
αα ϕ
α
j
n
j
xCR x
jJ j U
()
&
(), ()
,():
∈≥
∀= ∃ = ⊂ −
∞
supp
0
1
выполняется свойство 3.
ϕ
j
x() - выполняются свойства 1 и 2.
Теорема о разбиении единицы доказана.
Теорема о продолжении функции.
Частный случай - продолжение из прямоугольников.
KxRxa
KxRx
a
n
i
a
n
i
=∈ <
=∈ >
+
:
:
n
s
ns
0
Продолжение функции из
K
a
+
в K
a
.

www.uchites.ru
20
Лемма 1.
∀∈
+
fCK
k
a
() ∃∈FCK
k
a
() - продолжение функции f:
Fx fx x K
a
() () ( )=∈
+
и FCf
CK C K
k
a
k
a
()
++
≤
F
H
I
K
1
1.Определить функцию.
2.Проверить условие сливания: совпадание значений функции и её производных по
x
i
до k-
го порядка.
Доказательство.
Определим
Fx
fx x K
Af x
x
i
xK
a
i
n
i
k
a
()
(),
,,
=
∈
′
−
F
H
G
I
K
J
∈
R
S
|
T
|
+
=
+
−
∑
1
1
(2)
Коэффициенты
A
i
из условия:
xx x
n
=
−
( ,..., )
11
A
i
sk
i
s
i
k
−
F
H
G
I
K
J
==
=
+
∑
1
10
1
1
, ,..., (3)
lim ( ) lim ( )
(,) (,)
(,) (,)
xx
i
i
k
nn
Fx Fx
Af x f x
fx fx
→+ →−
=
+
=
′
=
′
′
=
′
∑
00 00
1
1
00
00
Значит, функция непрерывна.
Теперь - доказательство совпадения производных.
lim ( ) ( )( , )
lim ( ) lim ( ) , .
()( ,) .
x
xx
i
n
i
k
i
i
k
n
nn
nk
DFx D f x
DFx A D f x
x
i
i
Dfx A
i
→+
→− →−
=
+
=
+
=
′
=
′
−
F
H
G
I
K
J
−
F
H
G
I
K
J
=
′
⋅−
F
H
G
I
K
J
∑
∑
00
00 00
1
1
1
1
0
1
0
1
α
α
αα
α
α
α
Выполняется одно уравнение из (3), и:
=
′
()(,)Df x
α
0 .
Значит:
FCK
k
a
∈
−
().
Неравенство (1) очевидно через определение нормы в
C
K
k
a
()
−
.
Замечание: из доказательства и свойства (6) пространств Соболева следует: можно перейти к
H
k
- пространству Соболева с выполнением этой теоремы, и (1) тоже справедливо.
Замечание: в силу того, что множество бесконечно дифференцируемых функций в
замыкании куба всюду плотно в пространстве
H
k
в этом кубе и в силу того, что протсранство
Соболева инвариантно относительно невырожденной гладкой замены переменных.
Лемма 2.
∀∈ ∃
∈
=
∈
+
+
fHK FHKFx fx xK
k
a
k
aa
() ():() () при и
FCf
HK HK
k
a
k
a
() ( )
≤
+
2
(4)
Теорема о продолжении функции.
Пусть
QR
n
⊂ - ограниченная область, граница
∂
QC
k
∈
. Пусть Q ⊂
Ω
(Ω⊂
R
n
- область),
тогда:
