Лекции - Моделирование систем

Подождите немного. Документ загружается.

Имитационное моделирование

121

Очевидно, что правил перестановок A можно предложить весьма

большее число и все они будут давать какие-то определенные (иногда,

внешне весьма схожие) виды корреляционных функций. Главное здесь то,

что каждое правило A воспроизводит свой природный механизм корреля-

ции.

Пример 4.16. Используя перестановочный алгоритм с правилом ми-

нимизации модуля первой разности, прогенерировать пять случайных рав-

номерно распределенных в интервале [0,9] чисел. Параметр упорядочения

положить равным трем (n= 3).

Решение 4.16. Для генерирования потребуется семь цифр, имеющих

равномерное распределение вероятностей, которые мы будем выбирать из

первого столбца таблицы случайных цифр (приложение 2). Итак, мы вы-

брали числа: 1,3,0,9,1,6,3.

В соответствии с описанным выше алгоритмом

)

(

)

(

))

(

)

(

Реализуем правило перестановки, для чего находим модули первых

разностей )0()1(u

ξ− :

;213)0()1(u

=−=ξ−=∆

√ ;110)0()1(u

=−=ξ−=∆

,819)0()1(u

=−=ξ−=∆

среди которых компонент u

(1) дал минимальный модуль первой разности.

Следовательно, ξ(1)=u

(1)=0 и

).9,1,3())1(u),4(),1(u()2(U

Вновь произведем перестановку

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

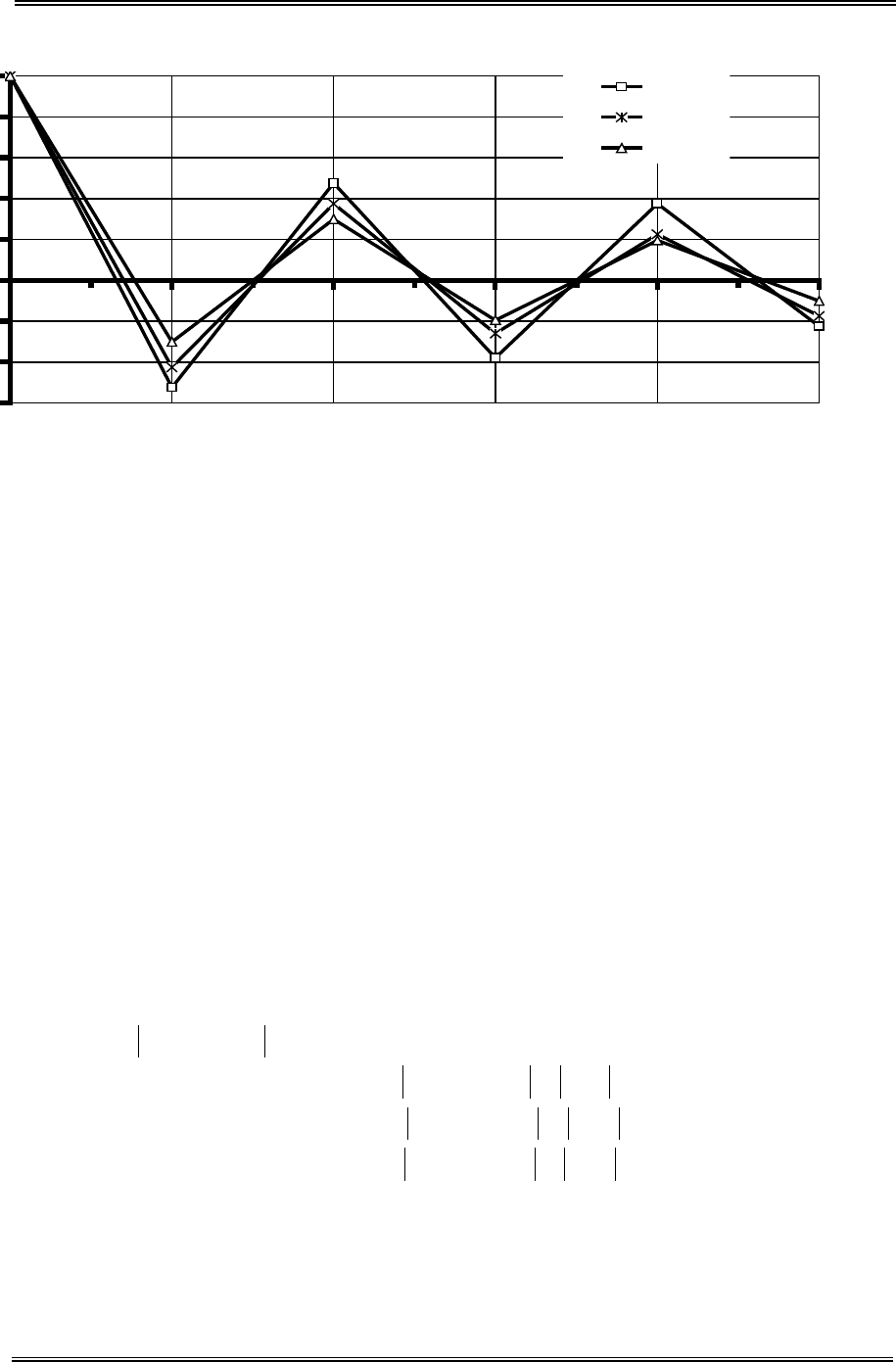
1 2 3 4 5

n=12

n=8

n=4

Рис. 4.10. Знакопеременные автокорреляционные функции.

Имитационное моделирование

122

;303)1()2(u

=−=ξ−=∆

√ ;101)1()2(u

=−=ξ−=∆

,909)1()2(u

=−=ξ−=∆

Тогда ξ(2)=u

(2)=1 и )9,6,3())2(u),5(),2(u()3(U

. На третьем ша-

ге ξ(3)=u

(3)=3 и )9,6,3())3(u),3(u),6(()4(U

. И, наконец, на четвер-

том шаге ξ(4)=u

(4)=3. (Отметим, что, если в результате осуществления

правила перестановки имеются несколько равноценных претендентов на

выбор в качестве нового генерируемого числа, то отбор из этих претенден-

тов проводится по произвольному правилу).

Итак, нами получена реализация равномерного случайного процесса

ξ(0)=1, ξ(1)=0, ξ(2)=1, ξ(3)=3, ξ(4)=3, имеющего экспоненциально-

косинусную корреляционную функции.

Основными недостатками перестановочных методов являются их

приближенный характер, обусловленный невозможностью точного зада-

ния корреляционных свойств.

Выше нами рассматривались алгоритмы упорядочения, позволяющие

моделировать случайные процессы с требуемым одномерным законом

распределения вероятностей, а также с требуемой формой и приближен-

ными значениями автокорреляционной функции. В том случае, когда ис-

следователь имеет заданную аналитически или таблично автокорреляци-

онную функцию, он вынужден обратиться к специальным таблицам для

поиска соответствующих алгоритмов упорядочения. В [43] предлагается

алгоритм замкнутого упорядочения, значительно упрощающий процедуру

имитации: достаточно на вход алгоритма подавать некоррелированный

случайный процесс с требуемым законом распределения вероятностей, но

нулевым математическим ожиданием, и коэффициенты корреляции, кото-

рые должны быть в выходном процессе. Пpи этом используется алгоритм

экстраполяции [22], который обеспечивает подбор ближайшего по модулю

первой разности значения из вектора не к ранее пpогенеpиpованному зна-

чению y(t-1), а к прогнозному, полученному посредством экстраполяции.

Описанные алгоритмы значительно расширяют области возможных

применений данного типа PR-методов, они просты в реализации и не зави-

сят от вида закона распределения вероятностей. Вместе с тем, следует от-

метить, что реализация замкнутого алгоритма упорядочения требует суще-

ственных затрат машинного времени в сравнении с разомкнутыми алго-

ритмами, так как необходимо на каждом такте реализовывать прогноз. По-

этому использование такого генератора в моделировании несколько сни-

жает его эффективность.

Пpиближенный характер алгоритмов упорядочения пpоявляется в не-

точности задания вероятностных свойств. Использование замкнутых алго-

Имитационное моделирование

123

ритмов или их дальнейшая модернизация могут привести к существенному

повышению точности. Но здесь необходимо соизмерять затраты на ис-

пользование алгоритмов упорядочения с затратами на использование ана-

литических методов. И, естественно, предпочтение следует отдать более

точным аналитическим методам при прочих равных условиях.

Имитационное моделирование сложных систем и особенно техноло-

гических процессов и автоматизированных систем управления требует соз-

дания таких источников случайных процессов с требуемыми статическими

и динамическими свойствами, которые позволяли бы воспроизводить кор-

реляционные свойства случайных процессов, изменяющиеся в широких

пределах. Пpи этом, без сохранения формы корреляционной функции, зна-

чения корреляционных моментов (в терминах алгоритмов упорядочения)

должны изменяться от значений, соответствующих n, до значений, соот-

ветствующих n+1. Это обусловлено тем, что, например, для таких элемен-

тов автоматизированных систем, как алгоритмы оперативного управления

технологическим пpоцессом, динамические свойства случайных процессов

могут быть заключены в некоторых пределах, определяемых значениями

производственных параметров. Пpи этом, границы этих интервалов, оче-

видно, не всегда соответствуют n и n+1. Подобные источники более при-

годны для имитации с точки зрения закона необходимого разнообразия

кибернетики, так как чем шире наши возможности в генерировании слу-

чайных процессов с заданными статистическими свойствами, тем большее

число различных ситуаций мы можем воспроизвести. Последнее заставля-

ет нас расширять функциональные возможности пеpестановочных проце-

дур. Приведенный ниже алгоритм упорядочения со случайным параметром

[30,32] позволяет снять ограничение, вызванное целочисленностью пара-

метра упорядочения.

Пусть x(0),x(1),... - реализация некоррелированного случайного про-

цесса с требуемым для воспроизведения одномерным законом распределе-

ния вероятностей и n

min

и n

max

- граничные значения параметра упорядоче-

ния.

Эта реализация порождает векторный случайный процесс U случай-

ной размерности

U(t)={u

(t),u

(t),...,u

(t)}, n(t)>1.

Величина n(t) (текущее значение параметра упорядочения) определя-

ется как целочисленная случайная величина с законо м распределения ве-

роятностей, ограниченным условием

(x)=0, x∈[n

min

max

] (4.17)

во всем остальном оставаясь произвольным.

Имитационное моделирование

124

Один из компонентов вектора U для каждого целого t>0 превращается

в элемент y(t) реализации случайного процесса Y(t) = u

(t), где индекс k

определяется упорядочивающим оператором

{

}

n(t),1,2,...,j , )1t(y)t(u min)1t(y)t(u

=−−=−−

причем в начале каждого цикла упорядочения разыгрывается значение

параметра упорядочения и принимается

(t+1)=u

(t), j≠ k,

(t+1)=x(t+n(t+1)).

Алгоpитм дополняется начальными условиями

y(0)=x(0),

U(1)={x(1),x(2),...,x(n(1))}.

Данный алгоритм является обобщением вышеописанных разомкнутых

алгоритмов: если в этих алгоритмах параметр упорядочения детерминиро-

ван, то в описываемом алгоритме этот параметр является случайной вели-

чиной с законом распределения вероятностей, ограниченным условием

(4.17), во всем остальном оставаясь произвольным. В этом случае возмож-

ности варьирования характеристиками автокорреляционных функций ге-

нерируемых случайных процессов существенно расширяются: мы можем

выбирать подходящие распределения, их параметры, использовать в каче-

стве параметра упорядочения зависимые и независимые случайные вели-

чины и тому подобное.

Изменение параметров закона pаспpеделения вероятностей параметра

упорядочения позволяет получать область возможных значений корреля-

ционных моментов значительно более широкую, нежели при упорядоче-

нии по предыдущему алгоритму. Одновpеменно стохастичность параметра

упорядочения решает задачу генерирования случайных процессов, более

пригодных для имитации с точки зрения закона необходимого разнообра-

зия.

Увеличение среднего значения параметра упорядочения приводит к

соответствующему увеличению значений коppеляционных моментов.

Подбиpая специальным образом значения параметров закона распределе-

ния P

(x) можно получить достаточно произвольную автокорреляционную

функцию. Пpи этом, область возможных значений корреляционных мо-

ментов ограничивается кривыми автокорреляционных функций, получен-

ных посредством разомкнутого алгоритма упорядочения с соответствую-

щим упорядочивающим оператором при параметрах упорядочения n

min

max

. В [32] более подробно представлены результаты экспериментальных

исследований данного многопараметрического алгоритма упорядочения и

даны некоторые его версии, предназначенные для расширения функцио-

нальных возможностей пеpестановочных процедур данного типа.

Имитационное моделирование

125

Обpатимся теперь к дальнейшему расширению областей применения

пеpестановочных PR-методов.

Следует отметить, что P- и R-методы со всеми присущими им досто-

инствами и недостатками получили развитие и для многомерных случай-

ных процессов. Имеет место [12], например, многомерный версии обрат-

ного преобразования (P-метод) и метода линейных преобразований (R-

метод) для воспроизведения случайных векторов с заданной корреляцион-

ной зависимостью. К сожалению, аналитические трудности, усугубленные

размерностью генерируемого процесса, не позволили построить достаточ-

но эффективных и простых в использовании PR-методов для многомерных

случайных процессов и случайных полей [29,38].

Pассматpивая алгоритмы упорядочения, укажем на возможность их

широкой модернизации с целью генерирования стохастических объектов

новой содержательной природы - многомерных случайных процессов и

случайных полей.

Отличительной особенностью всех известных алгоритмов упорядоче-

ния является то, что перестановке подвергаются отдельные значения слу-

чайного процесса. Естественно сформировать алгоритм упорядочения (на-

зовем его разомкнутым многопараметрическим алгоритмом упорядочения

групп), основанный на перестановке не отдельных элементов исходного

процесса, а отдельных групп значений этого процесса [30].

Пусть размер группы определяется величиной s, s∈S, S={1,2, ...} и

каждая группа имеет номер p∈P, P={0,± 1, ± 2,...}, а k - такое дополнение к

текущему номеру t, что (t+k)/s=p, то есть

. p

:u mink













Пpедположим, что x(0),x(1),... - реализация исходного случайного не-

коррелированного процесса {X(t),t∈T}, T={1,2, ...} с требуемым законом

распределения вероятностей и M[X(t)]=0. С учетом этих обозначений мно-

гопараметрический разомкнутый алгоритм упорядочения групп представ-

ляется в следующем виде [30,32].

Пусть x(1),x(2),... - реализация некоррелированного случайного про-

цесса {X(t),t∈T}, T={1,2,...} с требуемым одномерным законом распреде-

ления вероятностей.

Эта реализация порождает векторный случайный процесс

U(t)={u

(t),u

(t),...,u

(t)], n>1.

Величина n - параметр упорядочения. Каждый компонент вектора U

опpеделяется как некоторая интегральная характеристика от s значений

исходного процесса u

(t)=φ[x(l)].

Здесь φ - некоторая характеристика, объе-

диняющая s значений случайного процесса в качестве аргумента которой

указан первый из s элементов объединяемой группы.

Имитационное моделирование

126

Один из компонентов вектора U для каждого целого t>0 превращается

в группу элементов y(t),y(t+1),...,y(t+s-1) реализации генерируемого слу-

чайного процесса y(l)=x(l), l=t,t+1,..., t+s-1; r=q, q+1,...,q+s-1, где индекс q

определяется упорядочивающим оператором

{

}

n.1,2,...,j , )]1t(y[)t(u min)]1t(y[)t(u

=−ϕ−=−ϕ−

В начале каждого цикла упорядочения принимается

(t+1)=u

(t), j≠ q,

(t+1)=ϕ[x(s⋅(t+n))].

Алгоpитм дополняется начальными условиями

y(i-1)=x(i), i=1,2,…,s;

U(1)={u

(1),u

(1),...,u

(1)}=

={ϕ[x(s+1)], ϕ[x(2(s+1))], …, ϕ[x(n(s+1))]}.

Pезультатом работы такого алгоритма будет случайный процесс {Y(t),

t∈T}, t={0,1,...}, состоящий из гpупп, каждая из которых имеет длину s.

Пpи этом преобразовании вводится новая корреляция между элементами

разных групп, а внутри группы она остается прежней [32].

В [32] приводится обоснование того, что генерируемый алгоритм упо-

рядочения групп процесс является периодически коррелированным с пе-

риодом s [16]. В [16] доказана теорема, устанавливающая взаимосвязь ме-

жду периодическим случайным процессом с периодом s и s-меpным слу-

чайным процессом. Пpи этом, условия, накладываемые теоремой, при ис-

пользовании такого метода генерирования удовлетворяются.

Таким образом, представленный выше алгоритм позволяет генериро-

вать многомерные случайные процессы (и, при незначительной его модер-

низации [30,32], случайные поля), что существенно расширяет возможно-

сти имитационного моделирования.

Анализ результатов исследований многомерных версий алгоритмов

упорядочения показал, что независимо от перестановки реализаций мно-

гомерного случайного процесса или случайного поля динамические свой-

ства внутри реализации не изменяются, что подтверждает справедливость

предположения о сохранении корреляционных свойств внутри реализации

многомерного случайного процесса или случайного поля, а корреляцион-

ные свойства различных компонентов многомерного случайного процесса

или случайного поля зависят от расположения компонента в реализации и

определяется видом упорядочивающего оператора и параметрами упоря-

дочивающей процедуры.

Следует отметить, что все описанные выше и некоторые другие

пеpестановочные процедуры, а также их развития [27,28] имеют и техни-

ческую реализацию в виде специализированных устройств [1-4], либо

встроены в соответствующие пакеты прикладных программ [21,30].

Имитационное моделирование

127

Важным вопросом разработки и применения алгоритмов упорядоче-

ния является вопрос о законе распределения вероятностей воспроизводи-

мого случайного процесса и ряде других его вероятностных свойств.

Одной из таких попыток исследования следует назвать вероятностный

анализ алгоритма упорядочения, предназначенного для генерирования

марковских случайных процессов [14,17,26,41]. Пpедставленные в [34] ре-

зультаты позволяют сказать, что пеpестановочные процедуры данного ти-

па имеют весьма широкие и до сих пор ничем не ограниченные области

применения.

В заключение отметим, что принцип перестановки значений может

быть применен и для воспроизведения псевдослучайных процессов. На-

пример, в условиях ограниченности исходной реализации, предназначен-

ной для использования в имитационном моделировании, вызванной труд-

ностями получения информации или другими причинами, возникает задача

воспроизведения новой реализации, обладающей, помимо большего объе-

ма, еще и теми же (или близкими к ним) вероятностными свойствами.

Пpедлагаемые в [38] методы искусственного увеличения длины реализа-

ции связаны с явным искажением вероятностных свойств. В [3,4,28,34]

предлагается ряд новых пеpестановочных алгоритмов, решающих постав-

ленную задачу.

Pассмотpенные в данном пункте две группы PR-методов (аналитиче-

ские и пеpестановочные) обеспечивают принципиальную возможность

решения новых задач, недоступных ранее. Например, многомерные

пеpестановочные алгоритмы позволяют воспроизводить случайные векто-

ры не только с заданными законами распределения вероятностей, но и с

требуемыми корреляционными свойствами по осям координат (внутри

вектора и между векторами различающуюся).

Пpи этом, аналитические методы, претендуя на высокую точность,

весьма сложны в практическом использовании. Пеpестановочные же мето-

ды менее точны в воспроизведении вероятностных свойств, но существен-

но более технологичны в применении. К тому же, они обеспечивают до-

вольно высокую точность генерирования, достаточную для решения инже-

нерных задач. И, конечно, весьма важным является их большее быстродей-

ствие, в сравнении с аналитическими PR-методами.

4.2.3. Методика построения имитационных моделей.

Рассматривая вопросы методологии построения имитационных моде-

лей, следует сказать, что не существует какой-либо технологии типа набо-

ра команд, которая бы позволяла пользователю строить имитационные мо-

дели систем различных классов. (Это, по-видимому, характерно для любых

Имитационное моделирование

128

видов моделирования). Известные методологии (агрегативный подход Н.П.

Бусленко [9,10], динамическое моделирование [42], специальные языки

моделирования, например, [46]), не позволяют строить модели весьма

сложных систем. Но они весьма полезны при построении имитационных

моделей подсистем и элементов этих систем.

После построения модели решается вопрос об использовании компь-

ютера. В подавляющем большинстве случаев, когда речь идет о построе-

нии имитационной модели, исследователь принимает решение о реализа-

ции модели на компьютере. В [45] достаточно подробно рассмотрены пра-

вила и даны рекомендации по выбору типа вычислительной машины и

языка программирования для реализации модели. К сожалению, часто этот

выбор определяется типом имеющегося компьютера и теми языками, ко-

торыми владеет исследователь.

4.2.3.1. Агрегативный подход [9,10].

Существующие математические схемы описания сложных систем об-

ладают одним существенным недостатком. Он состоит в том, что единым

образом можно описать лишь те системы, элементы которых описываются

одной и той же математической схемой.

Наиболее существенным с теоретической и практической точки зре-

ния является случай, когда элементы системы описываются разнородными

математическими схемами. Из-за отсутствия единого формального описа-

ния элементов трудно рассчитывать на создание общих методов исследо-

вания систем в целом, а также единого подхода к классификации сложных

систем, изучению общих свойств важнейших классов систем их анализу и

синтезу. Даже такой, казалось бы, универсальный метод, как статистиче-

ское моделирование, для достаточно сложных систем с разнородными па-

раметрами описания элементов оказывается весьма громоздким.

Таким образом, введение унифицированной абстрактной схемы, по-

зволяющей единообразно описывать все элементы системы, имеет сущест-

венное значение.

Унифицированной абстрактной схеме придается достаточно общий

вид, с тем, чтобы она охватывала разнообразные темы реальных систем.

Для этого унифицированная схема должна иметь динамический характер,

быть способной описывать обмен сигналами с внешней средой и учиты-

вать действия случайных факторов.

Исходя из требований такого рода, в качестве унифицированной схе-

мы можно было бы взять стохастическую систему (задача стохастического

управления). Однако столь общая абстрактная схема имеет свои отрица-

тельные стороны. Чрезмерные обобщения неизбежно приводят к обедне-

Имитационное моделирование

129

нию содержания теории - для систем столь общего вида характерны лишь

тривиальные общие свойства.

Поэтому в [9,10] была предложена унифицированная схема, названная

агрегатом. Она образована из стохастической системы общего вида кон-

кретизацией операторов переходов и выходов.

Агрегат оказывается удобной схемой для описания широкого класса

реальных объектов. Кроме того, представление реальных систем в виде аг-

регатов позволяет изучить некоторые их общие свойства, связанные со

структурой и функционированием. Реализация на ЭВМ алгоритмических

(по сути, имитационных) моделей агрегата дает возможность решать мно-

гие задачи количественного и качественного анализа сложных систем.

Понятие агрегата.

Пусть T - фиксированное подмножество рассматриваемых моментов

времени; X, Г, Y, Z - множества любой природы. Элементы указанных

множеств будем называть так:

t∈T - моментом времени,

x∈X - входным сигналом,

g∈Г - управляющим сигналом,

y∈Y - выходным сигналом,

z∈Z - состоянием.

Состояния, входные, выходные и управляющие сигналы рассматри-

ваются как функции времени; их значения в момент t будут обозначаться

z(t), x(t), y(t) соответственно.

Под агрегатом понимается объект, определяемый множествами

T,X,Г,Y,Z и операторами H и G. Операторы H и G называют операторами

переходов и выходов. Они являются, вообще говоря, случайными и пред-

назначены для реализации функций z(t) и y(t). Структура операторов пере-

ходов и выходов выделяет агрегаты среди прочих систем.

Дополнительно вводится пространство параметров В. Пусть элемент

этого пространства В имеет вид β=(β

, …, β

)∈B. Значение β фиксировано

в рамках каждой конкретной задачи. Это конструктивный параметр. В этой

связи управляющий сигнал y(t) является параметром управления.

Рассмотрим сначала реализацию оператора выходов G. Представим

его в виде двух операторов G' и G". Оператор G' вырабатывает очередные

моменты выдачи непустых выходных сигналов, а оператор G" - содержа-

ние сигналов. Операторы эти строятся следующим образом.

В пространстве состояний агрегата Z для каждого β∈B и g∈Г опреде-

лим некоторое множество Z

,β)⊂Z, вид которого зависит от (g, β). То

есть множество Z

,β) в общем случае изменяется при изменении пара-

метров агрегата, когда осуществляется переход к условиям другой задачи.

В рамках данной задачи - в моменты поступления новых управляющих

Имитационное моделирование

130

сигналов g(t). В интервалах времени между моментами поступления

управляющих сигналов множество Z

,β) не изменяется и остается та-

ким, каким оно оказалось в момент поступления последнего управляющего

сигнала.

Множество Z

,β) определяет моменты выдачи выходных сигналов.

Оператор G" определяет содержание сигналов y=G"{t, z(t), g(t), β}.

В общем случае оператор G" является случайным оператором. Это

значит, что данным t, z(t), g(t) и β ставится в соответствие не один опреде-

ленный y, а некоторое множество значений управляющего параметра y с

соответствующим распределением вероятностей, задаваемых оператором

G".

Обратимся теперь к оператору переходов H.

Наряду с состоянием агрегата z(t) рассматриваются также состояние

z(t+0), в которое агрегат переходит за “малый” интервал времени. Вид

оператора H зависит от того, поступают или не поступают в течение рас-

сматриваемого интервала времени входные и управляющие сигналы. По-

этому его представляют в виде совокупности случайных операторов.

Пусть t'

- момент поступления в агрегат входного сигнала x'

, тогда

z(t'

+0)=V'{t'

, z(t'

), g(t'

), x'

, β}, (4.18)

где под g(t'

) понимается последний управляющий сигнал, поступивший в

момент времени t< t'

Если t"

- момент поступления в агрегат управляющего сигнала g''

, то

z(t"

+0)=V"{t"

, z(t"

), g''

, β}, (4.19)

Далее, если t'

- момент одновременного поступления в агрегат и

входного x

, и управляющего g

сигналов, то

z(t

+0)=V'{t

, V"(t

, z(t

), g

, x'

, β), g

, x

, β}. (4.20)

В этом выражении под V"{•} понимается не оператор, а результат его

действия на аргументы t

, z(t

), g

, β, являющийся элементом множества Z.

Другими словами, вместо (4.20) можно записать

z(t

+0)=V'{t

, z'(t

+0), g

, x

, β},

где z'(t

+0) определяется соотношением (4.19) для t

, z(t

), g

, β.

Наконец, если полуинтервал (t

n+1

] не содержит моментов поступле-

ния сигналов, за исключением t

n+1

, а t

- момент поступления входного или

управляющего сигнала, то для t∈(t

, t

n+1

]

z(t)=U{t, t

, z(t

+0), g(t

), β}.

Здесь, подобно (4.18), под g(t

) понимается последний управляющий

сигнал, поступивший в момент t≤t

Перейдем теперь к описанию типичного процесса функционирования

агрегата в терминах рассматриваемой выше реализации операторов H и G.