Лекции - Моделирование систем

Подождите немного. Документ загружается.

Имитационное моделирование

141

Информационная сеть занимает особое положение в связи с тем, что

она служит связующим материалом. В общем случае информационная сеть

начинается от уровней и темпов в пяти других сетях и заканчивается у

функций решений, определяющих темпы в этих сетях. Основная часть мо-

дели будет находиться внутри информационной сети, так как информация

– основа для принятия решений.

Для описания общей структуры динамической модели предприятия

необходима система уравнений. Она должна соответствовать обстановке и

взаимодействиям всех элементов моделируемой системы и процессам вы-

работки решений. Модель должна достаточно полно отражать наши пред-

ставления о реальной системе. Уравнения, которые мы будем рассматри-

вать, образуют основную систему, разработанную в соответствии с уже

описанной структурой модели. Будем рассматривать основные классы

уравнений, а не особые формы, которые могут принимать отдельные урав-

нения.

В основном система уравнений состоит из уравнений двух типов –

уравнений уровней и уравнений темпов. Для более полного понимания су-

ти уравнений следует рассмотреть вопрос о последовательности вычисле-

ний.

Система уравнений записывается вместе с определенными условиями,

устанавливающими способ ее решения. В динамическом моделировании

рассматриваются системы уравнений, которые регулируют изменяющиеся

во времени взаимодействия переменных. Эта изменчивость предопределя-

ет необходимость периодически решать уравнения для нахождения новых

состояний системы.

Для каждого момента времени может существовать специфическая

последовательность вычислений, определяемая характером системы урав-

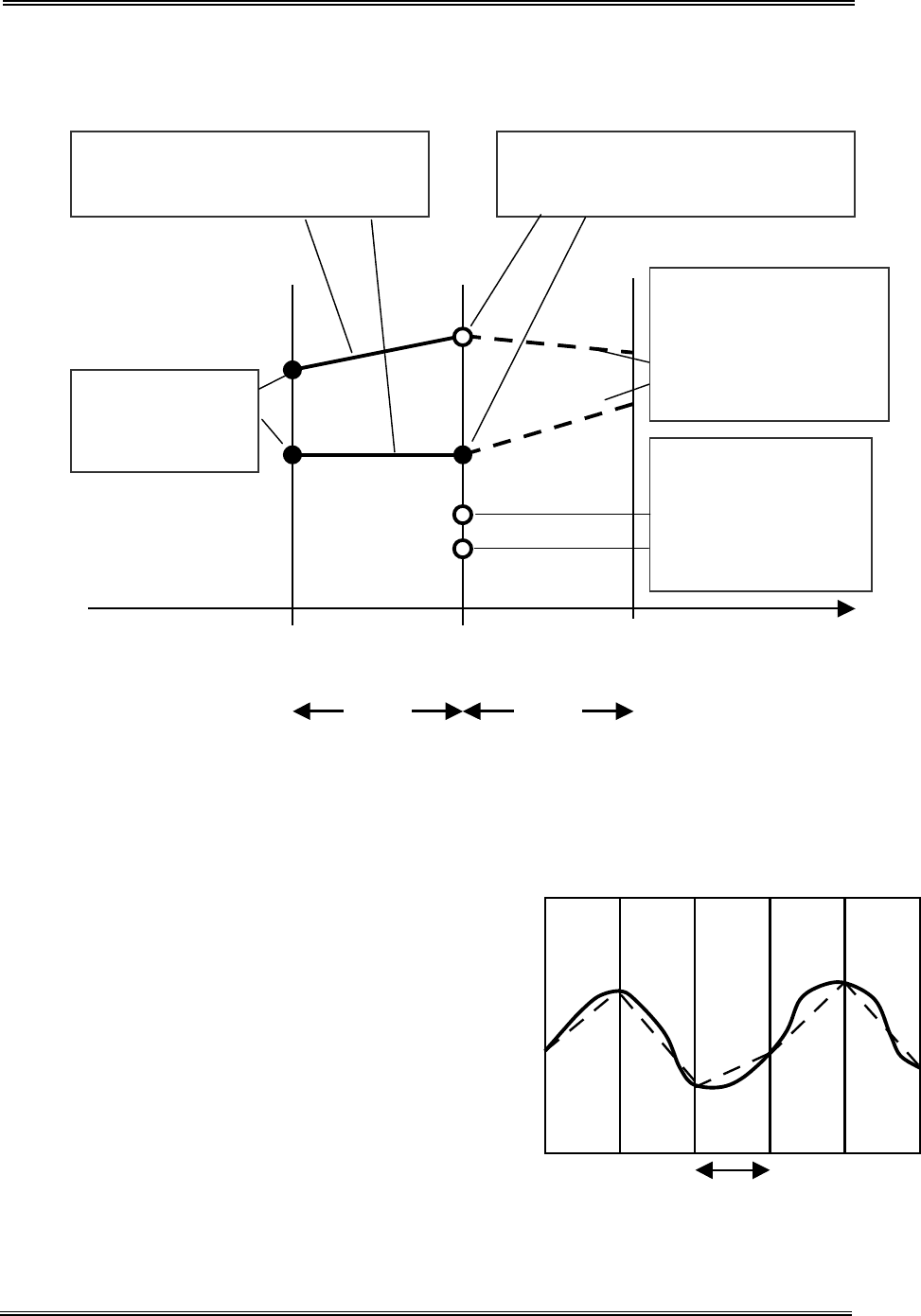
нений. На рис. 4.13 представлена последовательность, используемая в

данном случае.

Интервалы времени должны быть достаточно короткими, чтобы мож-

но было принять допущение о постоянстве темпа потока на протяжении

интервала, получив при этом удовлетворительное приближение к непре-

рывно изменяющимся темпам реальной системы. Это означает, что на

решения, принятые в начальной точке интервала, не будут влиять

изменения, происходящие в течение этого же интервала. Новые значения

уровней рассчитываются на конец интервала. По ним определяются новые

темпы (решения) для следующего интервала. Ясно, что можно выбрать

столь небольшие интервалы времени, что отрезки прямых, проведенных в

пределах каждого интервала, будут сколь угодно близко приближаться к

любой кривой (рис. 4.14). Практически возможно выбирать интервал столь

короткий, сколь это необходимо. Однако он должен быть таким, чтобы

объем вычислений не превышал возможностей современных

Имитационное моделирование

142

лений не превышал возможностей современных персональных компьюте-

ров.

В большинстве динамических мо-

делей допустимый интервал между

вычислениями определяется запазды-

ваниями. Запаздывания имеют вид по-

казательной функции. Существует эм-

пирическое правило выбора интерва-

ла. Он должен быть обязательно

меньше продолжительности любого

запаздывания. Желательно, чтобы он

был меньше его половины.

Наилучший способ проверки пра-

вильности выбора интервала решений

состоит в варьировании его величины

Рис. 4.13. Последовательность вычислений.

(DT – интервалы времени равной длины).

Рис. 4.14. Выбор интервала времени

DT.

t - время

Вспомогательные

переменные, вы-

числяемые после

определения уров-

ней.

Темпы в предстоя-

щий период KL, ко-

торые должны быть

рассчи

таны в момент

времени К.

Уровни в момент времени К, ко-

торые предстоит рассчитать.

Известные постоянные темпы в

течение интервала JK.

Известные

уровни в мо-

мент J.

Имитационное моделирование

143

и наблюдении за влиянием ее на результаты вычислений.

Особым критерием, определяющим максимальную величину интерва-

ла решений, является взаимосвязь между значениями уровней и темпами

потоков, входящими в эти уровни и исходящими из них. Интервал реше-

ний должен быть достаточно коротким, чтобы суммарный входящий или

исходящий поток не вызывал больших изменений в содержании уровня за

один интервал решений.

Вернемся к рис. 4.13. Момент К используется для обозначения «дан-

ного момента времени». Интервал JK только что истек. Информацию о

нем, как и о предыдущих периодах, может быть использована при решении

уравнений. Информация об уровнях и темпах в последующее время вооб-

ще недоступна при решении уравнений в настоящий момент времени К.

Прогнозы не представляют собой будущей информации, они являются

лишь представлениями о будущем, основанными на полученной ранее ин-

формации.

Для целей численного решения основные уравнения модели разделе-

ны на две группы:

- группа уравнений уровней,

- группа уравнений темпов.

При рассмотрении какого-либо интервала времени в первую очередь

решаются уравнения уровней, а затем полученные результаты использу-

ются в уравнениях темпов.

Вспомогательные уравнения, которые будут рассмотрены ниже, вво-

дятся для удобства в том или ином случае. Они решаются сразу после ре-

шения уравнений уровней – до решения уравнений темпов.

Уравнения решаются для моментов времени разделенных интервалом

DT. Уравнения решаются каждый раз применительно к условным момен-

там времени J, K и L. Причем принимается, что К представляет «настоя-

щий» момент времени, то есть принимается допущение, что в процессе

решения мы как раз достигли момента времени К, но пока еще не решили

ни уравнений уровней в момент К, ни уравнений темпов в интервале JK.

Уравнения уровней показывают, каким образом можно определить

уровни в момент К, основываясь на знании уровней в момент J и темпов на

протяжении интервала JK. В момент времени K вся необходимая инфор-

мация может быть получена и получается из предшествующего интервала

времени.

Уравнения темпов решаются в настоящий момент К после того, как

решены уравнения уровней. Поэтому значения уровней в настоящий мо-

мент К могут служить вводами для уравнений темпов. Темпы в интервале

JK также доступны для исследования. Иногда их можно использовать при

Имитационное моделирование

144

вычислении других темпов. Но в принципе это не является правильным и

необходимым.

Величины, определяемые из уравнений темпов (решений), относятся к

темпам потоков, на которые будет осуществляться воздействие в течение

предстоящего интервала KL.

Постоянство темпов в пределах интервала DT определяет собой по-

стоянную скорость изменения уровней в течение этого интервала времени.

После определения уровней в момент времени К и темпов для интер-

вала KL время индексируется. Это означает, что точки J,K,L сдвигаются на

один интервал времени вправо. Уровни, только что вычисленные для мо-

мента времени К, считаются теперь уровнями в момент J. Темпы для ин-

тервала KL становятся темпами для интервала JK. Настоящий момент вре-

мени K сдвигается таким образом на один интервал времени продолжи-

тельностью DT.

Модель следит за изменением системы во времени таким образом, что

окружающая среда (уровни) обусловливает решения и действия (темпы),

которые в свою очередь воздействуют на окружающую среду. Таким обра-

зом, взаимодействия внутри системы происходят в соответствии с «описа-

нием», которое было принято за основу при составлении уравнений моде-

ли.

Для выражения величин в уравнениях модели выбирают символы,

напоминающие общепринятую терминологию, связанную с повседневной

практической деятельностью. Например, уровень работающих в момент J –

ЧРАБ.J; в момент K – ЧРАБ.К. Темп выпуска готовой продукции в интер-

вале от J до K – ВГП.JК; в интервале K-L – ВГП.KL.

Константы не имеют обозначения времени, так как они не изменяются

от одного интервала времени к другому.

Уравнения уровней. Уровни представляют собой переменное по вели-

чине содержимое резервуаров в системе. Они существовали бы и в том

случае, если бы система была приведена в состояние покоя и все потоки в

ней остановились. Значения уровней определяются заново для каждого из

последующих интервалов времени, для которых решаются уравнения.

Уровни изменяются с постоянной скоростью, но их значения в этом про-

межутке времени не вычисляются.

Например,

КГП.K = КГП.J + (DT) (ВГП.JK - ПГП.JK),

где КГП - фактический запас готовой продукции,

DT - приращение времени между решениями уравнений системы,

ВГП - выпуск готовой продукции,

ПГП - потребление готовой продукции.

Имитационное моделирование

145

Уравнения уровней не зависят одно от другого. Решение каждого из

них зависит только от информации, касающейся предшествующего момен-

та времени. Поэтому порядок решения уравнений уровней не имеет ника-

кого значения.

Уравнения темпов (функции решений).

Уравнения темпов определяют темпы потоков между уровнями в сис-

теме. Они решаются на основе данных о существующих в настоящее время

величинах уровней в системе. В свою очередь темпы потоков являются

причиной изменений в уровнях.

Уравнения темпов реализуют действия, которые должны произойти в

системе за следующий интервал времени.

Уравнения темпов, как и уравнения уровней, на протяжении каждого

интервала времени решаются независимо одно от другого. Взаимодействие

в системе происходит при последующем воздействии темпов на уровни,

которые затем в свою очередь оказывают влияние на темпы в более позд-

ние интервалы времени. Уравнение темпа определят действие, которое бу-

дет совершаться непосредственно в следующий момент.

Например:

K.ST

KL.OUT =

где OUT - темп исходящего потока (единицы в неделю),

ST - количество, находящееся в настоящее время в запаздывании

(единицы),

D - константа - средняя продолжительность времени, необходи-

мого для преодоления запаздывания (недели).

Вспомогательные уравнения. Уравнения темпа может нередко стать

очень сложным, если его действительно формулировать лишь на основе

уровней. Часто бывает удобно разбить уравнение темпа на отдельные час-

ти, которые носят название вспомогательных уравнений. Эти уравнения

являются промежуточными. Они могут быть подставлены одно в другое и

далее в уравнения темпов.

Вспомогательные уравнения решаются на момент времени К после

решения уравнений уровней. Это обусловлено тем, что для их решения ис-

пользуются данные о значениях уровней в тот же момент времени. Они

должны быть решены прежде уравнений темпов, так как получаемые при

этом результаты необходимы для подстановки в уравнения темпов. В от-

личие от уравнений уровней и темпов, вспомогательные уравнения нельзя

решать в произвольной последовательности.

Дополнительные уравнения. Эти уравнения применяются при опреде-

лении переменных, не являющихся частью структуры модели, но исполь-

Имитационное моделирование

146

зуемых при печати и графическом отображении величин, представляющих

интерес для понимания поведения модели.

Уравнения начальных условий. Они используются для определения ис-

ходных значений всех уровней (и некоторых темпов), которое должно

быть произведено до начала первого цикла решения уравнений. Они также

используются в начальный момент времени для вычисления значений од-

них констант, исходя из значений других. Уравнения начальных условий

решаются только один раз перед началом каждого проигрывания модели.

Каждое уравнение позволяет определить переменную величину с

помощью констант и других переменных. Уравнений должно быть столько

же, сколько и переменных (включая исходное уравнение, служащее источ-

ником значений для каждого из внешних вводов, используемых при моде-

лировании).

Символы в диаграммах потоков. Диаграммы потоков являются на-

глядным описанием (представлением) системы уравнений. Диаграмма по-

казывает взаимосвязи между уравнениями и придает ясность формализа-

ции системы. Она дает ту же информацию, что и система уравнений, но в

иной форме. Диаграмма является промежуточной формой представления

системы между словесным описанием и системой уравнений.

Диаграмма потоков должна строиться одновременно с формулирова-

нием уравнений, описывающих систему.

Символика для представления модели в форме диаграммы основана

на произвольном выборе, производимом с целью более ясного представле-

ния частных аспектов той или иной ситуации. Система символов в дина-

мическом моделировании учитывает наличие взаимосвязей в системе. Она

отличает уровни от темпов и отделяет друг от друга шесть систем потоков:

информации, материалов, заказов, денежных средств, рабочей силы, обо-

рудования.

Диаграмма показывает, какие факторы влияют на каждую функцию

решения (темп). Однако диаграмма не раскрывает какие функциональные

связи существуют внутри функций решения.

Имитационное моделирование

147

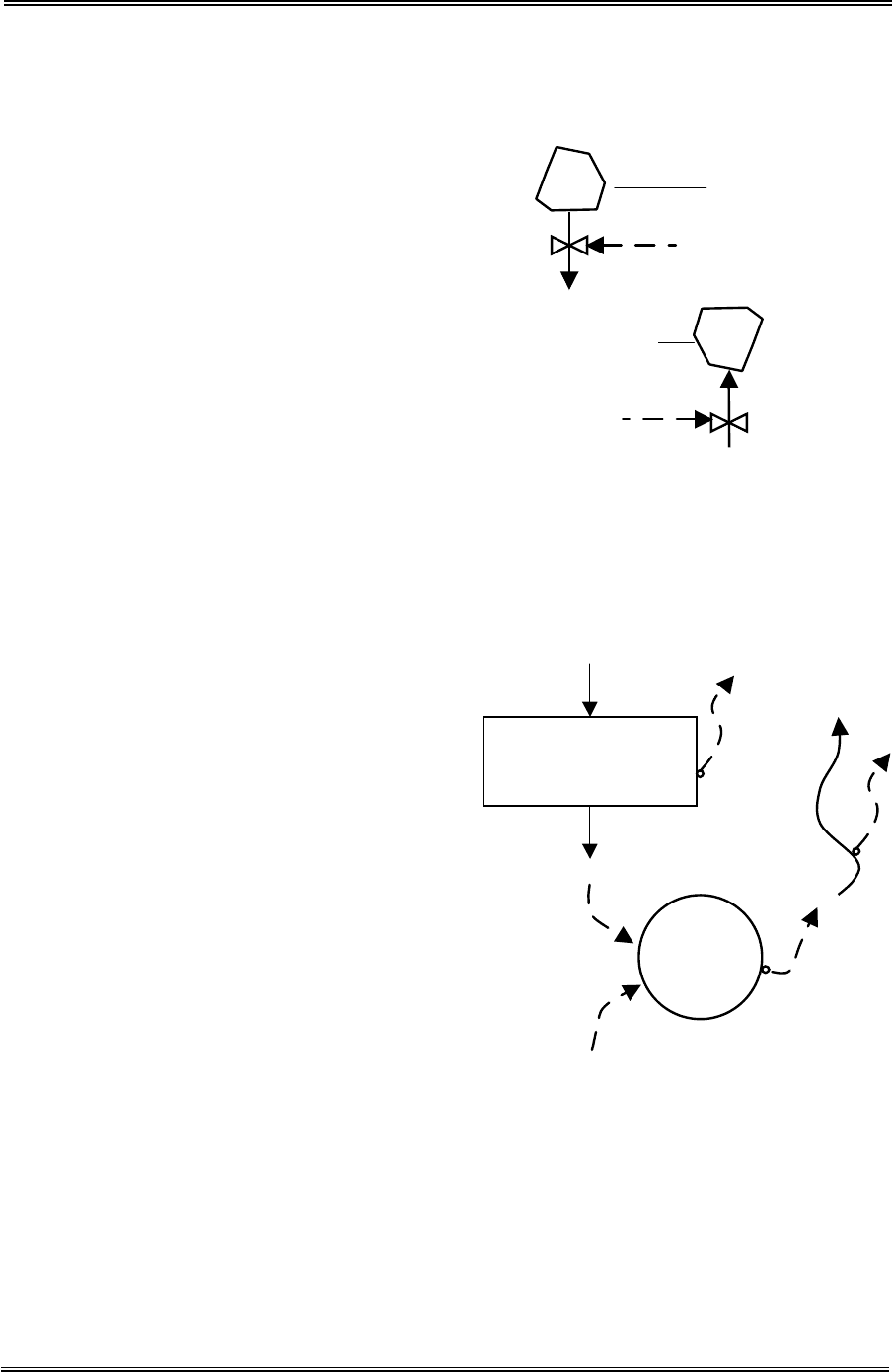
Истоки потоков и их конечные пункты. Часто бывает необходимо ре-

гулировать темпы потоков, истоки или конечные пункты которых не рас-

сматриваются в модели. Например, поток заказов должен откуда-то начи-

наться. Но точность терминологии,

используемой в системах потоков, не

допускает простого перехода инфор-

мационных линий в линии, символи-

зирующие заказы. В динамических

моделях предполагается, что заказы

начинаются там, где хранятся бланки

заказов. Но это не имеет отношения к

динамике модели. Точно так же вы-

полненные заказы должны быть изъя-

ты из системы в карточку выполнен-

ных заказов, которая обычно не имеет

существенных динамических характе-

ристик. При рассмотрении динамических моделей предполагается, что ха-

рактеристики источников и приемников не оказывают существенного

влияния на поведение системы.

Отбор информации. Пото-

ки информации связывают меж-

ду собой многие переменные в

системе. Отбор информации из

ее потока не оказывает воздей-

ствия на ту переменную, о кото-

рой собирается информация.

Вспомогательные уравне-

ния. Данный вид уравнений вы-

делен как независимое понятие из функций

решений, так как имеют самостоятельное зна-

чение. Они располагаются в каналах потоков

информации между уровнями и функциями

решений, которые регулируют темпы. Эти

уравнения могут быть алгебраически подставлены в уравнения темпов.

Рудник

Склад

SRR

IAR

6-1,L

SSR

IDR

6-3,A

Имитационное моделирование

148

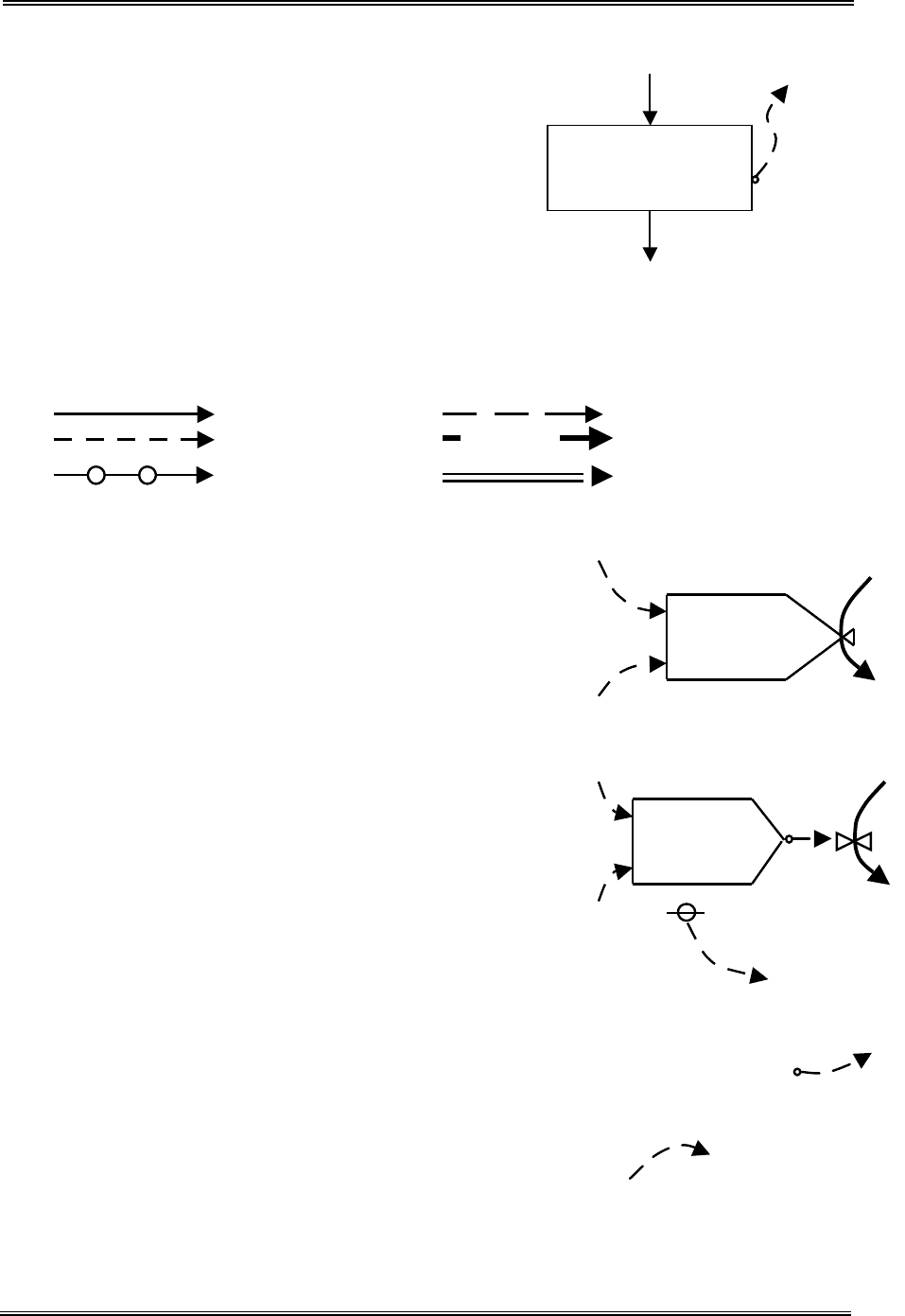
Уровни. Уровень изображается в

виде прямоугольника, в верхнем ле-

вом углу которого указывается обо-

значение переменной, характеризуе-

мой данным уровнем, а в правом

нижнем углу – номер уравнения.

Потоки. Потоки могут быть на-

правлены к уровню или от него.

Символ, относящийся к потоку, ха-

рактеризует и один из шести рассматриваемых типов потоков.

Материалы Денежные средства

Информация Оборудование

Заказы Рабочая сила

Функции решений (уравнения темпов). Функ-

ции решения определяют темп потока. Они дей-

ствуют, как вентили в каналах потоков, и поэтому

изображаются соответствующими символами.

Могут быть использованы две эквивалентные

формы символов потоков. Они изображают не

только решения, но и регулируемый поток

(сплошная линия) и ввода информации (пунктир-

ные линии), которые определяют темп потока.

Здесь же приводится номер уравнения, описы-

вающего величину темпа потока.

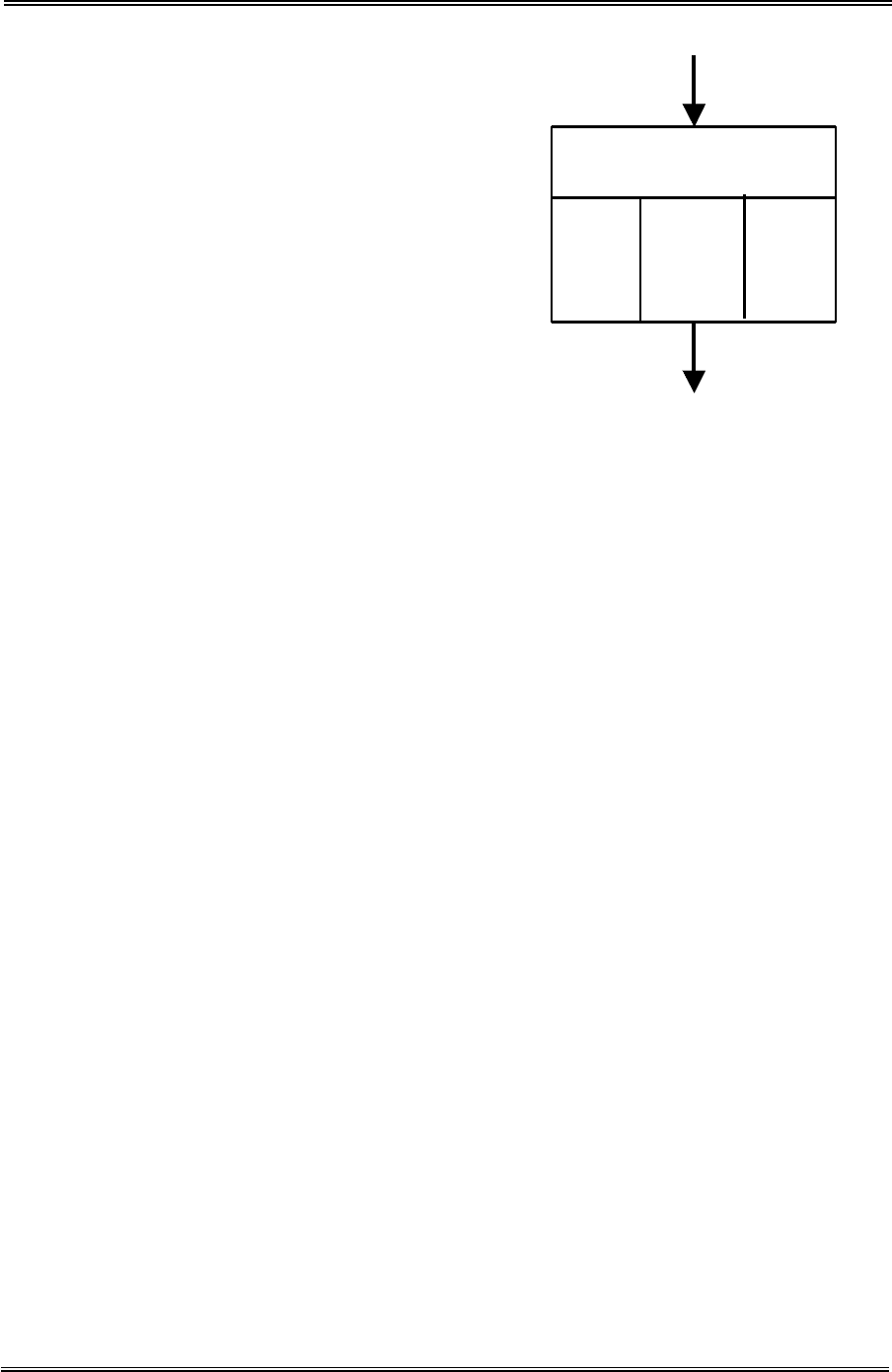
Параметры (константы). Многие числовые

величины, которые описывают характеристики

системы, принимаются постоянными (по крайней

мере на время вычислений в ходе одного проиг-

рывания модели).

Переменные на других диаграммах. Данное

обозначение используется, если диаграмма систе-

мы делится на отдельные части. Кроме обозначе-

ния уравнения может также указываться номер

страницы.

SRR

IAR

6-1,L

SSR

6-5,L

SSR

6-5,L

DUR

(DFD 13-24,A)

(MTR 13-17,L)

Имитационное моделирование

149

Запаздывания. Запаздывания пред-

ставляются совокупностью уровней и тем-

пов потока. Но частота использования вы-

нуждает ввести дополнительный символ.

SSD - темп на входе,

MTR - количество (уровень), пере-

мещаемое потоком,

13-17,L – уравнение для определения

количества MTR,

D3 - порядок запаздывания,

SRR - темп на выходе,

13-18,R - уравнение для определения

темпа на выходе,

DTR - постоянная времени запаздывания.

Этот символ заменяет три уровня со связывающими их между собой

темпами (для запаздывания третьего порядка – D3). D1 указывало бы на

запаздывание первого порядка. DTR – среднее время, необходимое для

преодоления запаздывания. Подробнее о запаздываниях и примеры по-

строения динамических моделей смотрите в [ 42].

4.2.3.3. Индивидуальное моделирование

В отличие от ранее рассмотренных методик построения имитацион-

ных моделей будем понимать под индивидуальным моделированием такие

разработки имитационных моделей, которые носят сугубо индивидуаль-

ный, уникальный характер. Это имитационные модели, разработанные для

исследования конкретных систем.

Рассмотрим пример такой имитационной модели, позволяющий ис-

следовать функционирование простейшего склада. Пусть на нем обеспечи-

вается поступление, хранение и выдача потребителю некоторой детали.

Для полноты картины будем считать, что все процессы, описывающие по-

ведение склада, носят вероятностный характер. Ясно, что детерминизация

какого-либо процесса приведет лишь к упрощению модели.

Введем следующие обозначения (рис. 4.15):

t - текущее время, t=1,2,…,

- состояние склада в момент времени t,

min

- минимально допустимое состояние склада,

max

- максимально допустимое состояние склада,

- сигнальный уровень (R

≥0),

- спрос на деталь в момент времени t (ε

≥

0),

- размер поставки деталей от поставщика (Q

≥0),

SRR

13-18,R

DTR

MTR

13-17,L

SSD

SRR

Имитационное моделирование

150

- время выполнения заказа на поставку (τ>0),

p - вероятность дефицита детали.

При поступлении спроса ε

в момент времени t состояние склада S

уменьшается на величину этого спроса. При достижении состоянием скла-

да некоторого сигнального уровня R

вырабатывается запрос потребителю

на поставку партии деталей. Через случайное время τ эта партия размером

поступит на склад и увеличит его состояние. Сигнальный уровень пред-

назначен для управления процессом пополнения содержимого склада. В

процессе функционирования склада возможна ситуация дефицита, когда

состояние склада S

может стать отрицательным (в математическом смыс-

ле). Это возможно в том случае, если в процессе потребления содержимое

склада будет исчерпано, а поставка партии деталей не произошла. Для

управления состоянием склада будем использовать параметр р – вероят-

ность дефицита.