Лекции - Моделирование систем

Подождите немного. Документ загружается.

Имитационное моделирование

101

первой цифры таблиц, получим следующие четыре трехзначных числа:

180, 276, 299, 379.

Второй способ получения первичных случайных чисел заключается в

использовании технических устройств - датчиков или генераторов случай-

ных чисел. В качестве таких могут применяться механические (рулетка,

кубик, и т.п.), электронные (резисторы, диоды, электронные лампы и т.п.),

радиоактивные и другие типы устройств. На выбор конкретного типа уст-

ройства оказывают влияние ряд факторов: стабильность параметров гене-

рируемых сигналов, взаимозаменяемость элементов, срок их службы, ус-

ловия эксплуатации, простота ис-

точника преобразований сигнала и

т.п. После определения типа источ-

ника требуется сконструировать

преобразователь случайного сигна-

ла, основное назначение которого

состоит в преобразовании получен-

ного первичного случайного сигна-

ла в форму, пригодную для исполь-

зования в вычислительном устрой-

стве. Приведем пример такого ге-

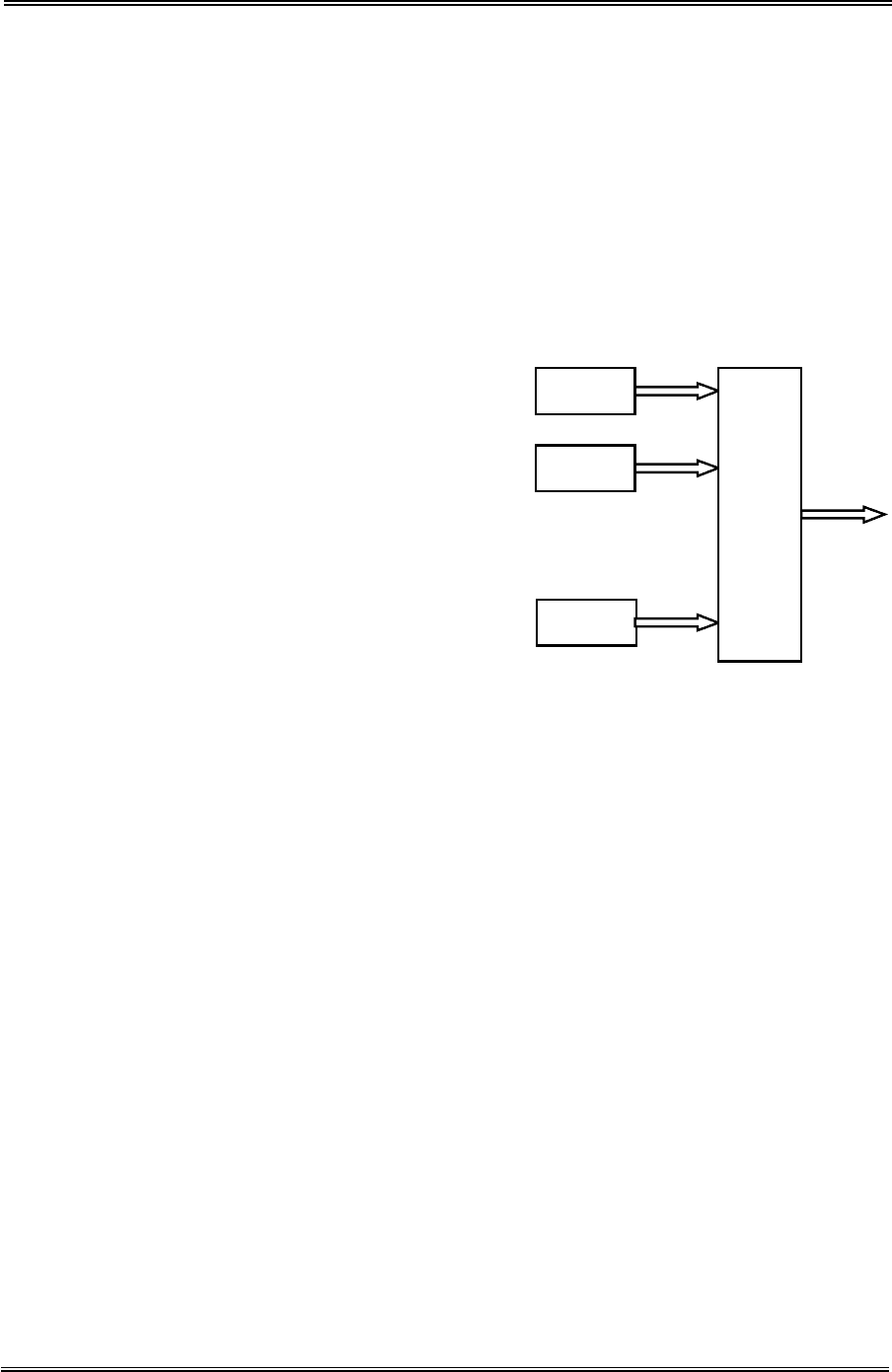
нератора (рис. 4.6) – [43]. Пусть мы

имеем Κ генераторов стандартных

импульсов ГИ-j, которые воспроизводят детерминированные по свойствам

импульсы. В силу того, что каждый из генераторов не является идеальным

устройством, сигналы на их выходах Χ

будут иметь случайные от-

клонения от идеального. Эти отклонения не превышают допустимых. Объ-

единяя все сигналы Χ

элементом ИЛИ, будем получать выходной сигнал

Υ, который по своей сути (в силу неидеальности генераторов) будет пред-

ставлять собой последовательность импульсов со случайными параметра-

ми, например, амплитудой.

Рис. 4.6. Датчик случайных чисел.

ГИ

Имитационное моделирование

102

И, наконец, третьим способом

получения первичных случайных

чисел являются методы генериро-

вания псевдослучайных чисел. При-

годность случайных чисел опреде-

ляется в конечном счете не процес-

сом их получения, а тем, удовле-

творяют ли они некоторым приня-

тым тестам. Но в таком случае со-

вершенно безразлично как эти числа получены (они могут быть даже со-

считаны по какой-то формуле). Главное, чтобы они удовлетворяли тестам.

Числа ξ

, ξ

, …, ξ

, …, которые вычисляются по какой-либо формуле и

могут быть использованы вместо случайных чисел при решении некото-

рых задач, называются псевдослучайными числами.

Большинство алгоритмов, используемых на практике, представляют

собой рекуррентные формулы следующего вида:

n+1

=Φ(ξ

), (4.2)

где ξ

- задано.

Часто в качестве функции Φ выбирают следующую функцию ξ

i+1

=[Αξ

], где [] - знак целой части числа, а Α- некоторый множитель(Α>>1).

Важной чертой алгоритмов вида (4.2) является то, что при реализации

на компьютере они всегда порождают периодические последовательности.

В самом деле, так как в коде любого персонального компьютера можно за-

писать лишь конечное количество чисел, заключенных между нулем и

единицей (равномерное распределение в интервале [0,1]), то рано или

поздно какое-нибудь значение ξ

совпадает с одним из предыдущих значе-

ний ξ

Вместо формулы (4.2) можно попытаться использовать для получения

последовательностей псевдослучайных чисел более сложные рекуррент-

ные формулы

n+1

=Φ(ξ

, ξ

n+1

, … , ξ

n-r+1

считая, что начальные значения ξ

, ξ

, …, ξ

r-1

заданы. В [40] приведены ал-

горитмы, основанные на подобных формулах.

В качестве конкретных алгоритмов вида (4.2) можно назвать методы

усечения, вычетов, перемешивания и т.д.

Метод усечения. В качестве рекуррентного процесса берется произ-

вольное число ξ

, состоящее из 2n двоичных цифр. Величина ξ

возводится

в квадрат (состоящий уже из 4n цифр) и выбирает число ξ

из 2n средних

двоичных цифр (от n+1-й до 2n -й). В дальнейшем процесс повторяется в

той же последовательности.

Такой рекуррентный процесс не дает удовлетворительной (в смысле

Имитационное моделирование

103

некоррелированности) последовательности случайных разрядов, а распре-

деление полученных этим способом псевдослучайных чисел отклоняется

от равномерного.

Пример 4.3. Пусть ξ

=1011. Построить последовательность из трех

псевдослучайных чисел методом усечения.

Решение 4.3. ξ

=(1011)

=01111001. Отсюда ξ

=1110,

=(1110)

=11000100. Отсюда ξ

=0001, ξ

=(0001)

=00000001. Отсюда

=0000. Имеем последовательность: 1110, 0001, 0000.

Приведенный пример демонстрирует один из существенных моментов

в использовании методов генерирования псевдослучайных чисел: неудач-

ный выбор начальных констант может привести к вырождению последова-

тельности чисел, то есть получению последовательности нулей.

Способ произведений. Значительно лучшие результаты дает следую-

щее видоизменение метода усечений: выбирается произвольная пара чисел

и ξ

; составляется их произведение и его средние цифры используются в

качестве ξ

Данный рекуррентный процесс дает меньшее отклонение псевдо-

случайных чисел от равномерного распределения, чем метод усечения в

первоначальном виде.

Пример 4.4. Пусть ξ

=24 и ξ

=31. Построить последовательность из

трех псевдослучайных чисел методом произведений.

Решение 4.4. ξ

=0744. ξ

=74. ξ

=2294. Тогда ξ

=29. ξ

=2146. От-

сюда ξ

=14. Таким образом, получена последовательность: 74, 29, 14.

4.2.2.3. P-методы.

Методы генерирования некоррелированных случайных чисел с тре-

буемым одномерным законом распределения вероятностей носят название

Р-методов.

В зависимости от точности воспроизведения последовательности

случайных чисел одномерного закона распределения вероятностей Р-

методы можно разделить на точные и приближенные.

К числу точных Р-методов относятся метод обратных функций (метод

Н.В.Смирнова) и специальные методы, к приближенным - метод Неймана

и метод кусочной аппроксимации (метод Н.П. Бусленко) [12].

В дальнейшем будем использовать следующие обозначения:

η - случайное некоррелированное число, равномерно распределенное

в интервале [0,1] ;

ξ - случайное число с одномерным законом распределения вероятно-

стей, который требуется получить;

Имитационное моделирование

104

δ - случайное число с гауссовским (нормальным) законом распреде-

ления вероятностей.

Метод обратных функций. Суть метода состоит в подборе некоторого

преобразования исходных случайных чисел, трансформирующего равно-

мерное в интервале [0,1] распределение в требуемое F

(x) , где F

(x) -

функция распределения. Выбор преобразования осуществляется в соответ-

ствии со следующим предложением [12] .

Если ξ удовлетворяет уравнению

η=

∫

∞−

)t(dF , (4.3)

где η - величина, распределенная равномерно на [0,1], то ξ распределено

по закону F

(x).

Выражение (4.3) можно, очевидно, переписать и через плотность рас-

пределения вероятностей

η=

∫

∞−

dt)t(f , (4.4)

Ясно, что преобразование Н.В. Смирнова можно применить и для

дискретных распределений, соответственно представив уравнение (4.3).

Пример 4.5. Пусть требуется найти преобразование для генерирования

случайных чисел, распределенных по равномерному в интервале [a,b] за-

кону распределения вероятностей.

Решение 4.5. Плотность равномерного в интервале распределения

имеет вид:

)x(f

−

x∈[a,b].

В соответствии с формулой (4.4) имеем

∫∫∫∫

∞−

ξ−

−ξ

−

=+==η

dt)t(fdt)t(fdt)t(f

Отсюда

)

(

−

(4.5)

Пример 4.6. Найти преобразование для генерирования случайных чи-

сел экспоненциальным распределением







>λ

λ−

0x,0

,0x,e

)x(f

Решение 4.6. В соответствие с формулой (4.4) имеем

Имитационное моделирование

105

∫∫

λξ−λ−

∞−

−=λ==η

e1dtedt)t(f

Отсюда, после логарифмирования левой и правой части равенства

η−=

λξ

−

1e , получаем )1ln(

η−

−=ξ или, с учетом того, что η и (1-η) рас-

пределены равномерно в интервале [0,1] , можно записать

)ln(

−=ξ .

Пример 4.7. Построить процедуру получения биномиально распреде-

ленных случайных чисел.

Решение 4.7. Известно [44], что биномиально распределенная случай-

ная величина ξ есть число успехов в n независимых испытаниях Бернулли

с вероятностью успеха в каждом из испытаний p и вероятностью неудачи

q=1-p.

Тогда алгоритм генерирования биномиально распределенных чисел ξ

c параметрами n и р имеет следующий вид:

- устанавливается начальное значение биномиальной величины ξ=0;

- генерируется источником первичной случайности равномерно рас-

пределенное на интервале [0,1] случайное число η (разыгрывается испыта-

ние Бернулли);

- проверяется условие η<p (произошло ли событие в испытании Бер-

нулли?), если событие не произошло (η<р), то осуществляется переход к

шагу 5;

- если событие в испытании Бернулли произошло (η≥р), то биноми-

альная величина увеличивается на единицу;

- шаги 2,3,4 повторяются n раз.

Пример 4.8. Получить три случайных числа с распределением Бер-

нулли, если вероятность успеха в каждом испытании p = 0,4.

Решение 4.8. В соответствии с физическим механизмом, описываю-

щим испытания Бернулли, имеем следующий алгоритм генерирования:

- устанавливается начальное значение бернуллиевского случайного

числа ξ = 0;

- генерируется источником первичной случайности равномерно рас-

пределенное на интервале [0,1] случайное число η;

- проверяется условие η<0,4 (произошло ли событие в схеме Бернул-

ли?), если событие произошло (η≥0,4), то ξ=1. В противном случав (η<0,4)

число не изменяется, то есть ξ= 0.

На выходе процедуры получено случайное число ξ, имеющее распре-

деление Бернулли с вероятностью успеха р .

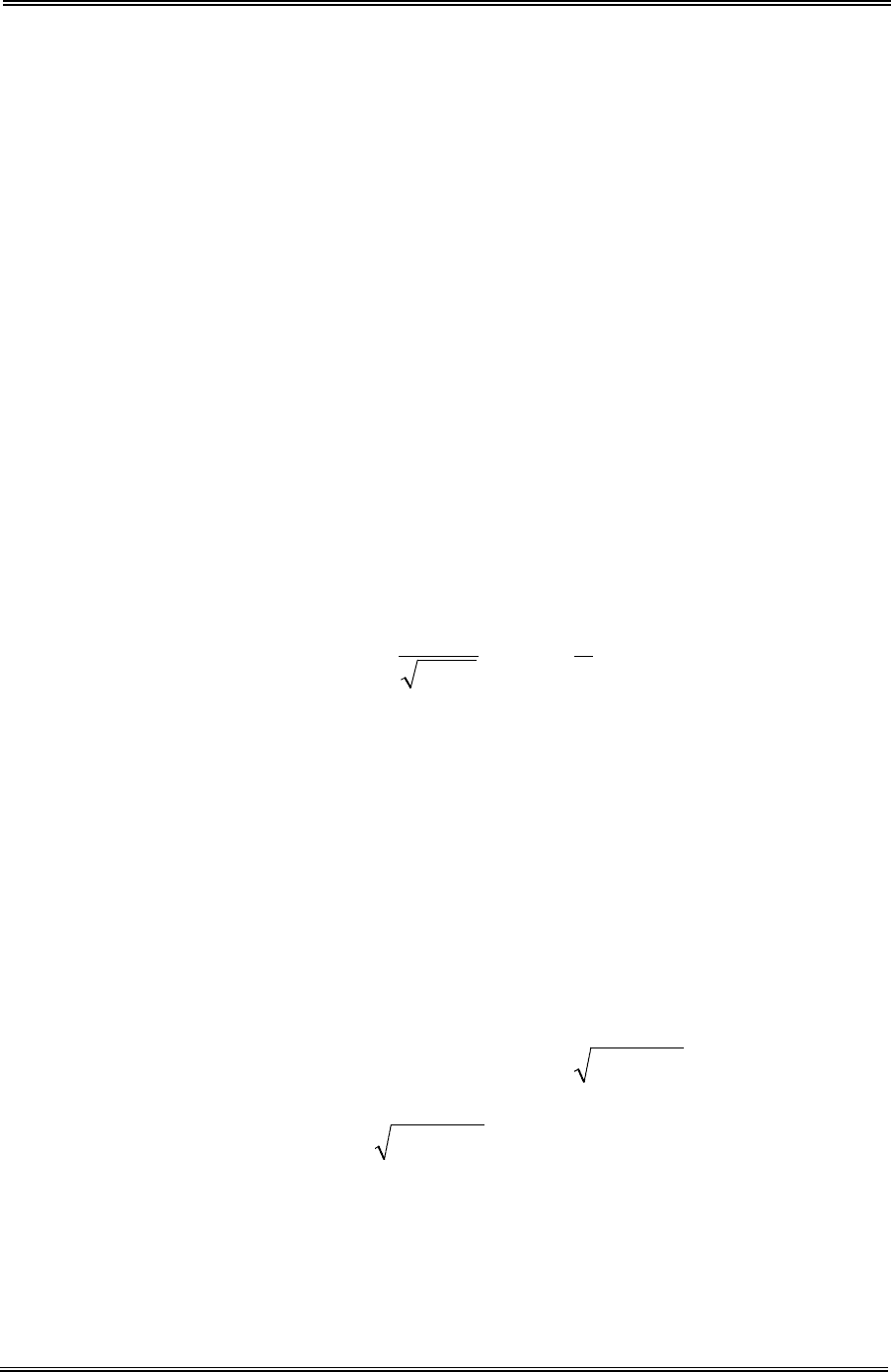
Имитационное моделирование

106

Для получения трех случайных чисел необходимо (в соответствии с

алгоритмом) три исходных числа η. Получим их из таблицы случайных

цифр (см. приложение 2). Ограничимся при этом двумя знаками после за-

пятой (заметим, что это ограничение зависит от точности задания парамет-

ров генерируемого распределения). Возьмем три первых пары цифр из

первой строки таблицы и запишем их в виде десятичной дроби:

=0,10; η

=0,09; η

=0,73.

Используя описанный выше алгоритм (р=0,4):

1) ξ

= 0;

2) η

≤ 0,4 (0,1 < 0,4). Следовательно, ξ

=0;

3) ξ

=0;

4) η

≤ 0,4 (0,09 < 0,4). Следовательно, ξ

=0;

5) ξ

=0;

6) η

>0,4 (0,73 > 0,04). Следовательно, ξ

=1.

Итак, получены три случайных числа 0,0,1, имеющих распределение

Бернулли с вероятностью успеха (появления события) р=0,4.

В соответствии с центральной предельной теоремой теории вероятно-

стей можно получить нормально распределенные случайные числа

12/k

−η⋅≈δ

∑

причем точность аппроксимации растет с ростом k. Для многих прак-

тических целей достаточно взять k=12, так что

∑

−η≈δ

Гауссовские случайные числа могут быть получены и как функции от

двух и большего количества чисел с другими, негауссовскими распределе-

ниями вероятностей, например, произведение двух чисел ξ

и ξ

, имеющих

одно распределение арксинуса, а другое - распределение Рэлея, имеет га-

уссовское распределение. Для генерирования чисел с распределениями

арксинуса и Рэлея может использоваться метод обратных функций

)2sin(

πη

ln2 η−=ξ

Тогда

)2sin(ln2

πη⋅η−=δ (4.6)

т.е. необходимо два исходных числа η

и η

, подвергнуть этому преобразо-

ванию.

Гауссовски распределенные числа являются основой для генерирова-

ния чисел с рядом распределений (в силу существующей взаимосвязи ме-

жду гауссовским и некоторыми другими распределениями). Так, например,

Имитационное моделирование

107

числа с распределением Рэлея могут быть получены из пары гауссовских

чисел

δ+δ=ξ

Числа с логарифмически нормальным распределением генерируются

преобразованием

σδ

−

=ξ me ,

где m и σ - параметры логарифмически нормального распределения.

Пример 4.9. Получить три гауссовских случайных числа, используя

центральную предельную теорему.

Решение 4.9. Для получения одного гауссовского числа по формуле

(4.6) необходимо 12 исходных чисел η. Выберем их из таблицы случайных

цифр (см. приложение 2) следующим образом: для δ

будем суммировать

12 первых чисел, записанных в виде двухзначной десятичной дроби, из

первой строки, для δ

- из второй, для δ

- из третьей строки. Тогда,

=(0,10+0,09+0,73+0,25+0,93+0,76+0,52+0,01+0,35+0,8б+0,34+0,67)-6,00=-

0,39;

=(0,37+0,54+0,20+0,48+0,05+0,64+0,89+0,47+0,42+0,96+0,24+0,80)-6,00=-

0,06;

=(0,08+0,42+0,26+0,89+0,53+0,19+0,64+0,50+0,93+0,03+0,23+0,20)-6,00=-

0,10.

Итак, получены три гауссовски распределенных случайных числа: δ

- 0,39; δ

= - 0,06; δ

= - 0,10.

Отметим, что в некоторых сборниках таблиц по математической ста-

тистике приводятся таблицы нормально распределенных случайных чисел

(приложение 3) с параметрами M[δ]=0 и σ[δ]=1. Используя формулу (4.6)

можно получить гауссовские случайные числа с иными параметрами и то-

гда следует (для приведения их к стандартному виду) произвести норми-

ровку.

Метод Неймана. Он относится к приближенным методам [12] и суть

его состоит в следующем:

- пусть закон распределения вероятностей, который требуется ввести

в последовательность случайных чисел, представлен плотностью f

(x), ог-

раниченной на интервале [a,b] и для которой, )};x(f{maxM

- для получения случайных чисел ξ с плотностью f

(x) генерируется

пара исходных чисел ),(

)k(

ηη , которая затем преобразуется в новую па-

ру чисел

)k(

(*)

)ab(a( η−+=η и )M

)k(

(*)

η⋅=η ;

Имитационное моделирование

108

- если

(*)

)(f η≥η

, то

)k(

η=ξ , в противном случае необходимо

вновь получить пару исходных чисел ),(

)1k(

ηη , преобразовать их по

тем же формулам в ),(

(*)

ηη , проверить условие и т.д.

Пример 4.10. Пусть требуется получить три случайных числа с зако-

ном распределения вероятностей







ππ−∉

−

∈

⋅

].2/,2/[x,0

],2/,2/[x),xcos(75,0

)x(f

причем М=0,75.

Решение 4.10. Будем получать пары исходных чисел из таблицы слу-

чайных цифр, выбирая в качестве η

две цифры, записанные в виде деся-

тичной дроби, из первого столбца, а для η

будем аналогично выбирать

цифры из второго столбца.

Тогда

)1(

η =0,10 и

)1(

η =0,09. Преобразуем пару (

)1(

η ,

)1(

η ) в новую па-

ру чисел

,4,02/

)1(

(*)

π−=η⋅π+π−=η

.0675,075,0

)1(

(*)

=η=η

Вычисляем 23175,0)4,0cos(75,0)(f

(*)

=π−⋅=η

, сравниваем )(f

(*)

η . Так как

(*)

)(f η>η

(0,23175 > 0,0675), то число

)1(

η принимаем в

качестве первого генерируемого случайного числа 1,0

)1(

=η=ξ . Делаем

аналогичные действия для второго числа

)2(

η и числа

)2(

η 37,0(

)2(

=η и

)54,0

)2(

=η . Имеем

;13,0)12()2/(

)2(

(*)

π−=−η⋅⋅π=η

;405,075,0

)2(

(*)

=η⋅=η

.9178,0)13,0cos(75,0)(f

(*)

=π−⋅=η

Так как

(*)

)(f η>η

(0,9178 > 0,405), то 37,0

)2(

=η=ξ . Третья пара

)3(

η = 0,08 и

)3(

η =0,42. Для этой пары

;42,0)12()2/(

)3(

(*)

π−=−η⋅⋅π=η

;315,075,0

)3(

(*)

=η⋅=η

.1865,0)42,0cos(75,0)(f

(*)

=π−⋅=η

Так как

(*)

)(f η<η

(0,1055 < 0,315), то пара ),(

)3(

ηη отбрасывает-

ся и для нее выбирается новая пара исходных чисел

)4(

η =0,99 и

)4(

η =0,01,

для которой

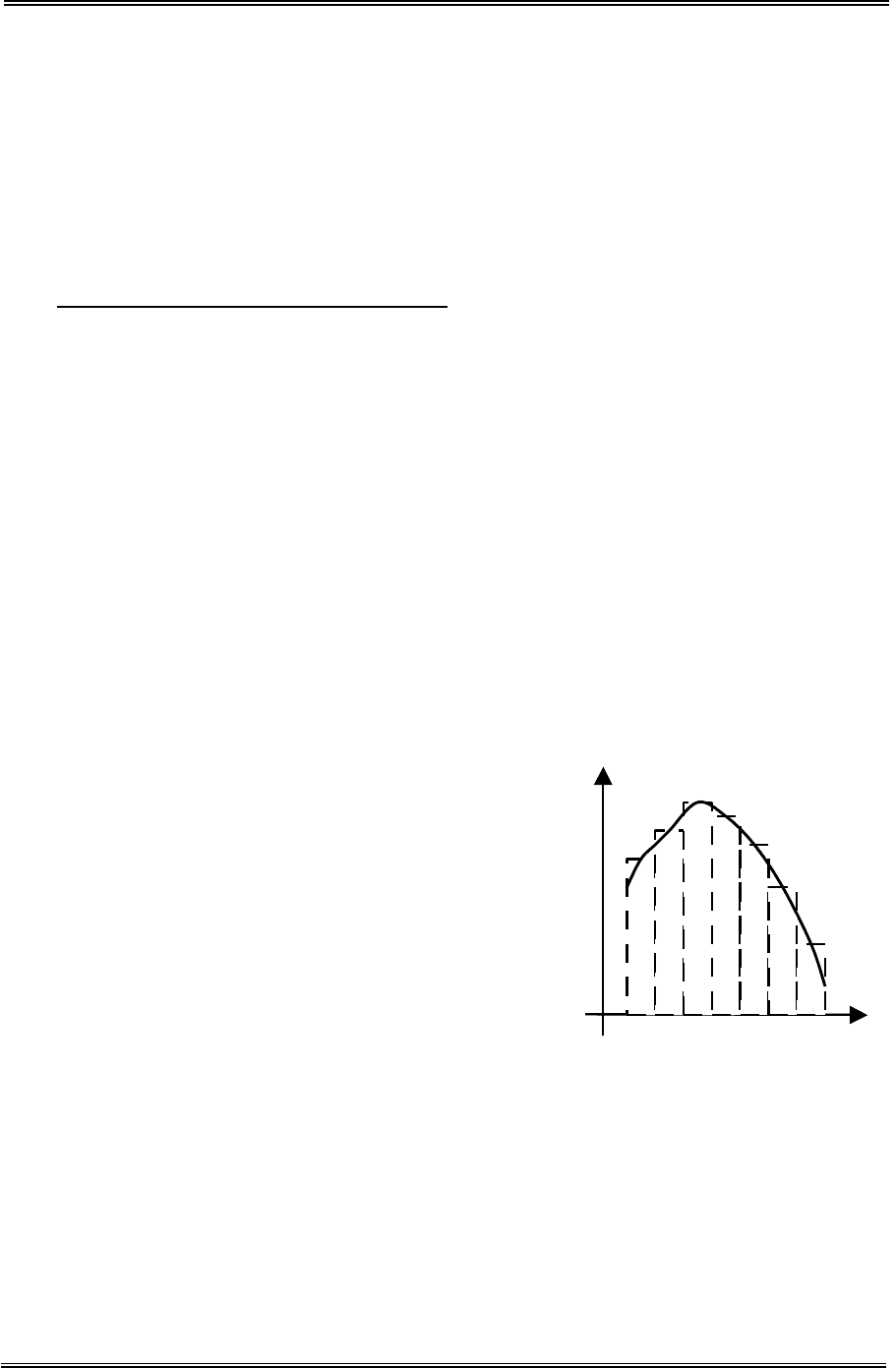
Имитационное моделирование

109

;49,0)12()2/(

)4(

(*)

π=−η⋅⋅π=η

;0075,075,0

)4(

(*)

=η⋅=η

.0708,0)49,0cos(75,0)(f

(*)

=π⋅=η

Так как

(*)

)(f η>η

(0,0706 > 0,0075), то 99,0

)4(

=η=ξ .

Итак, методом Неймана получено три случайных числа ξ

=0,1,

=0,37, ξ

=0,99.

Метод кусочной аппроксимации. Его сущность состоит в замене гене-

рируемого распределения вероятностей серией простых дискретных рас-

пределений, для которых можно указать достаточно удобные и простые

моделирующие процедуры [12].

Пусть требуется прогенерировать случайные числа с плотностью рас-

пределения f

(x). Предположим, что x∈[a,b] неограниченное распределе-

ние можно приближенно заменить ограниченным. Интервал [a,b] разбива-

ется на n достаточно малых интервалов (a

, a

m-1

), m=0,1,…,n-1, a

=a, a

=b,

так, чтобы заданное распределение в пределах этих интервалов можно бы-

ло достаточно точно аппроксимировать каким-нибудь простым распре-

делением, например, равномерным, трапецеидальным и т.д. В дальнейшем

рассмотрим кусочную аппроксимацию равномерным распределением.

Пусть P

- вероятность попадания случайного числа ξ в каждый из

интервалов (a

, a

m+1

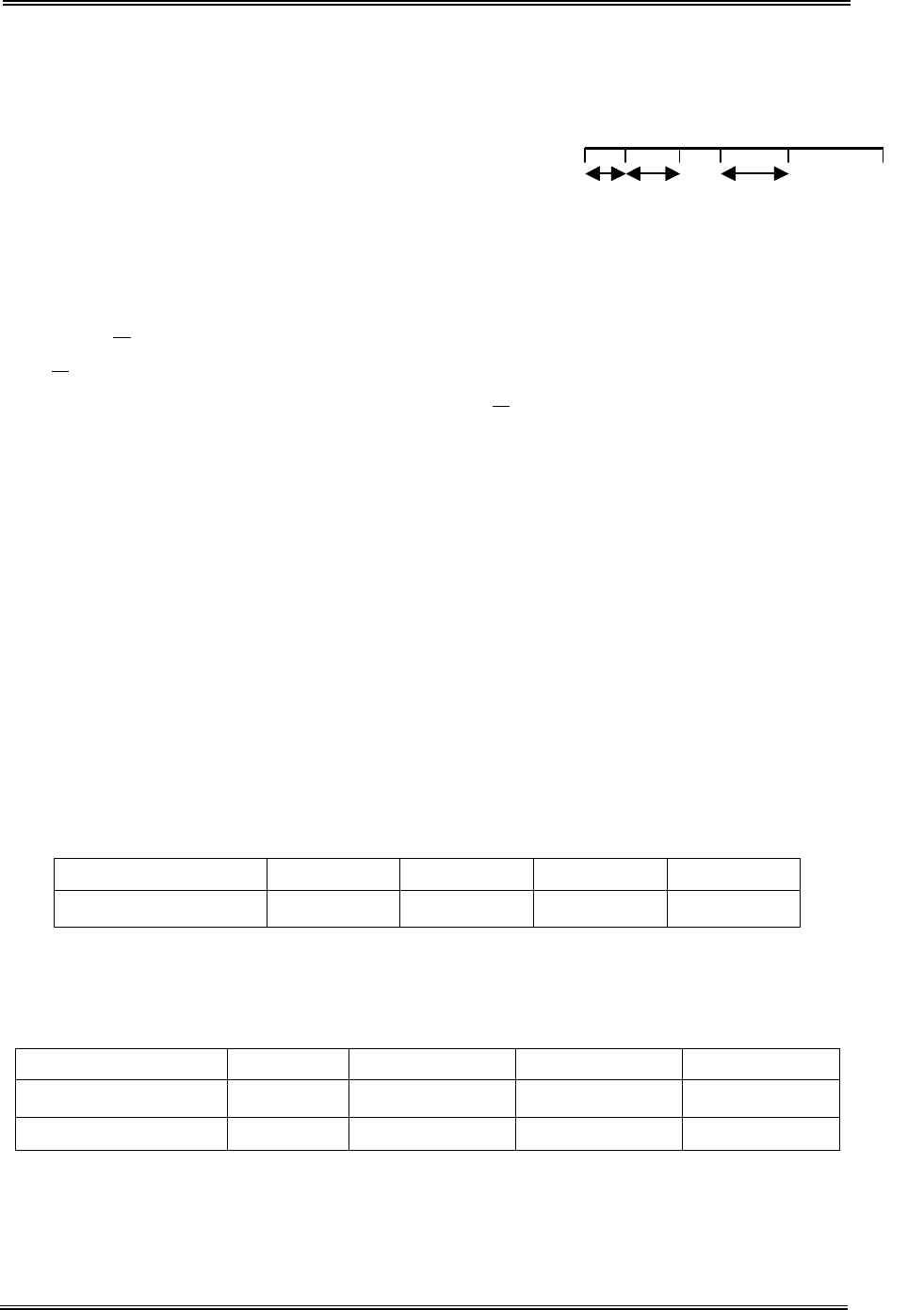
). Случайные числа ξ с кусочно-равномерным распре-

делением (рис. 4.7) можно получить в со-

ответствии со следующей схемой преобра-

зования случайных чисел:

- случайным образом с вероятностью

P выбирается, интервал (a

, a

m+1

);

- формируется число равномерно

распределенное в интервале (a

, a

m+1

), ко-

торое и будет ξ:

ξ=(a

m+1

- a

)⋅η + a

при этом η - случайное число, генерируе-

мое источником первичной случайности.

Рис. 4.7. Метод кусочной

аппроксимации.

. . . а

(x)

Имитационное моделирование

110

Случайный выбор интервала (a

, a

m+1

) с

вероятностью P

означает по существу моде-

лирование случайного числа, принимающего n

значений a

, m=0,1,…,n-1, с вероятностью P

каждое, что делается следующим образом. Ин-

тервал [0,1] разбивается на n интервалов (x

m+1

), m=0,1,…,n-1, x

=0, x

=1, длиной x

m+1

- x

= P

каждый (рис. 4.8).

Источником первичной случайности вос-

производится равномерно распределенное в [0,

1] число

. Путем последовательного сравне-

ния

с x

определяется интервал (x

, x

m+1

), то

есть тот интервал, в котором оказывается

, и, следовательно, соответст-

вующий интервал (а

, а

m+1

В основу этого процесса положен очевидный факт - вероятность по-

падания равномерно распределенной в интервале [0,1] случайной величи-

ны в некоторый подынтервал (x

, x

m+1

) равна длине этого подынтервала.

Метод кусочной аппроксимации обладает, в отличие от метода Ней-

мана, возможностями увеличения точности воспроизведения ве-

роятностных свойств. Для этого необходимо увеличить число малых ин-

тервалов (a

, a

m+1

), то есть n→∞, что приведет к снижению быстродействия

метода.

Пример 4.11. Пусть требуется прогенерировать методом кусочной

аппроксимации три случайных числа, если их закон распределения

вероятностей задан таблицей 4.1 (разбиение на малые интервалы (a

, a

m+1

)

произведено).

Таблица 4.1

, a

m+1

) (0,1) (1,2) (2,3) (3,4)

{

}

1mm

aaP

≤

0,2 0,3 0,4 0,1

Решение 4.11. Сформируем единичный отрезок для организации вы-

бора случайного интервала (a

, a

m+1

), m=0,1,2,3,4 (см. табл. 4.2)

Таблица 4.2

, a

m+1

) (0;1) (1;2) (2;3) (3;4)

{

}

1mm

aaP

≤

0,2 0,3 0,4 0,1

, x

m+1

)

(0,0; 0,2)

(0,2; 0,5) (0,5; 0,9) (0,9; 1,0)

Прогенерируем первое случайное число ξ

. Для этого разыграем (из

таблицы случайных цифр, приведенной в приложении 2, будем выбирать

пары цифр из 17-го и 18-го столбцов таблицы и формировать из них деся-

Рис. 4.8. Случайный выбор

интервала.

m+1

0 p

. . . p

. . . 1