Лекции - Моделирование систем

Подождите немного. Документ загружается.

Имитационное моделирование

не означает, что для количественной оценки наличия периодических со-

ставляющих не могут применяться статистические критерии, например,

критерий проверки гипотез о равенстве коэффициентов корреляции [20].

Особое значение нормальных (гауссовских) случайных процессов,

обусловленное их широким распространением на практике и наличием

обширных теоретических и прикладных исследований, позволяет сущест-

венно упростить как аналитическое, так и аппаратурное изучение свойств

случайного процесса. Поэтому одним из основных свойств процессов и яв-

ляется его нормальность.

Наиболее простым способом проверки на гауссовость реализации

случайного стационарного процесса является определение оценки плотно-

сти распределения и сравнение ее с теоретической нормальной плотно-

стью. При достаточно большой длине реализации и малых ошибках изме-

рений несоответствие теоретической и опытной кривых будет очевидным.

Тем не менее всегда желательно использовать статистические критерии

для оценки соответствия плотностей, наиболее популярным из которых

является критерий согласия Х

-квадрат [20,39].

В том случае, если статистическая проверка на нормальность реализа-

ции стационарного случайного процесса дает отрицательный результат,

это не означает, что продолжать исследования нет возможности. Просто

следует, используя различную справочную литературу (например, [44] или

приложение 1) или, исходя из физического смысла случайного процесса,

подобрать иной, отличный от гауссовского, закон распределения вероят-

ностей и проверить соответствующую гипотезу о соответствии этого тео-

ретического распределения опытным данным.

Таким образом, к числу основных свойств случайных процессов отно-

сятся стационарность, периодичность и нормальность.

Для оценивания этих свойств используются различные статистиче-

ские характеристики и критерии проверки гипотез о соответствии этих ха-

рактеристик теоретическим значениям или просто гипотезы о равенстве

их.

Если в распоряжении исследователя имеется несколько реализаций

одного случайного процесса или несколько реализаций различных случай-

ных процессов, то возникает необходимость изучения их взаимных веро-

ятностно-статистических свойств. В [7,8,14,15,17,20,37,39,41] приведены,

помимо определений совместных вероятностных характеристик, различ-

ные методы их оценивания и проверки гипотез. Получение и использова-

ние взаимных (совместных) вероятностных характеристик позволяет более

точно описывать и исследовать свойства объекта. Кроме того, в некоторых

случаях достигается сокращение объемов обрабатываемой информации за

счет объединения эквивалентных по свойствам реализаций.

Имитационное моделирование

4.2.1.2. Методика анализа временных рядов.

Будем считать, что исследователь решил все вопросы, связанные со

сбором, регистрацией и предварительной обработкой данных, и в его рас-

поряжении имеются зафиксированные в дискретной, цифровой форме на-

блюдения. Рассмотрим методику проведения последней операции - анали-

за данных.

Целью операции анализа данных является получение стационарной

составляющей реализации случайного процесса с выделением из отдель-

ной реализации всех нестационарностей и периодичностей, с фиксацией

порядка выделения и описаний нестационарностей и периодичностей, на-

хождение оценок и подбор теоретического закона распределения вероят-

ностей, наиболее точно в статистическом смысле описывающего распре-

деление реализации. Исследование начинается с анализа отдельных реали-

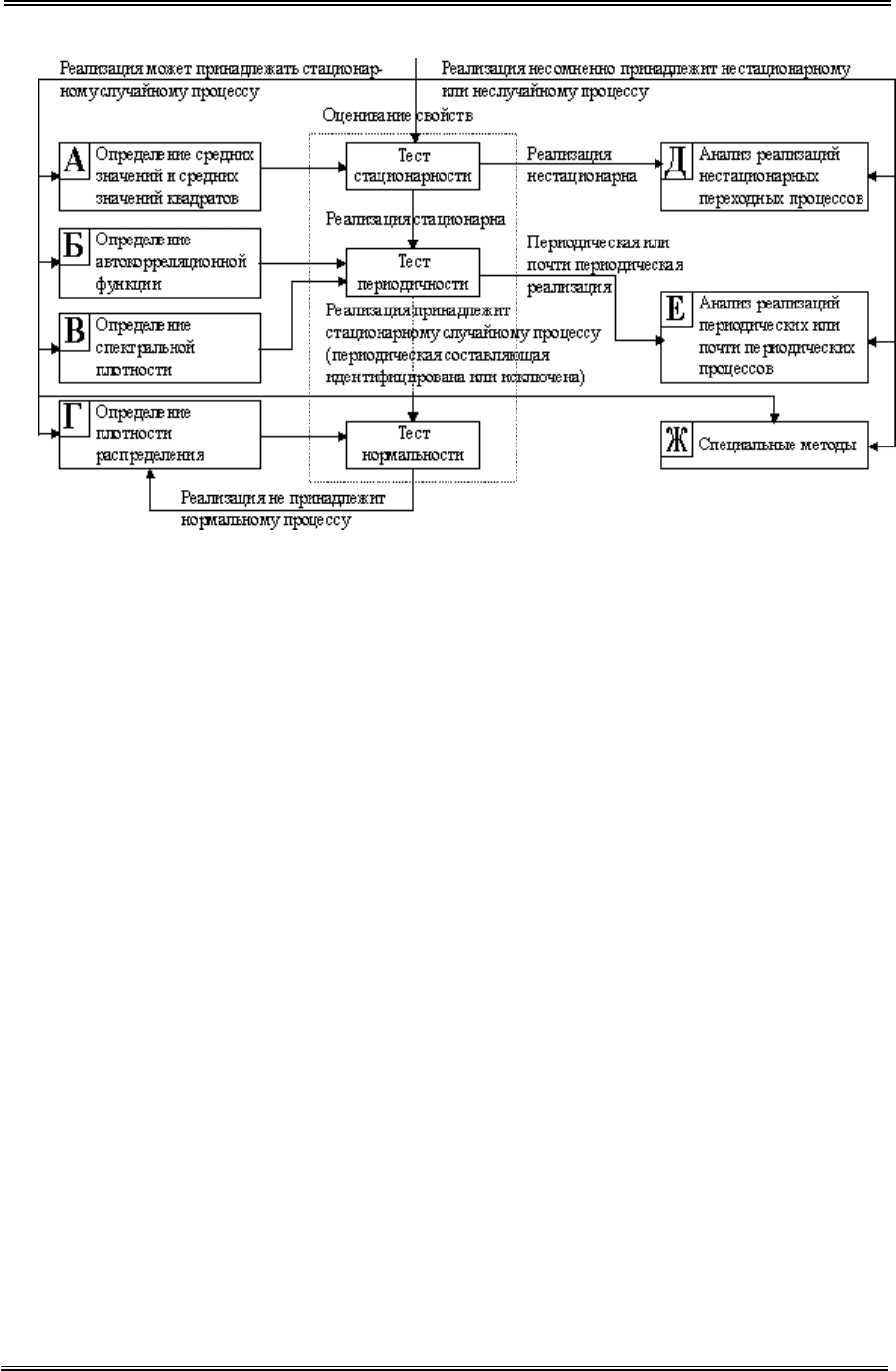
заций (рис. 4.4).

Визуальный просмотр реализаций призван выяснить, имеют ли место в

реализации нестационарность и периодичность. Если просмотр показал,

что процесс содержит подобные изменения, то необходимо провести их

анализ. При этом конечной целью является выделение временных измене-

ний из реализаций. С этой целью, исходя из физической сути процесса,

подбираются аппроксимирующие функции для нестационарности или пе-

риодичности, находятся параметры этих функций (для этого может ис-

пользоваться, например, аппарат регрессионного анализа [20,39]) и затем, с

помощью какой-либо арифметической операции, зависящей от характера

изменений, удаляют нестационарность и периодичность. Здесь могут ис-

пользоваться также специальные методы, привлеченные из других дисци-

плин исследования объектов.

Имитационное моделирование

Рис. 4.4. Анализ отдельной реализации.

После обнаружения временных изменений, оставшаяся реализация

передается вновь на начало схемы, и так повторяется до тех пор, пока при

визуальном просмотре не будет принято решение о том, что реализация

может принадлежать стационарному процессу. Если это решение принято,

то далее применяют точные количественные методы для оценивания ос-

новных свойств. При этом вычисляют оценки статистических характери-

стик - математического ожидания, дисперсии, автокорреляционной функ-

ции и других. Находится также гистограмма частот.

Все эти оценки используются для проведения тестов стационарности,

периодичности и нормальности. Причем, если хотя бы один из первых

двух тестов даст отрицательный результат (реализация содержит неста-

ционарность и/или периодичность), то необходимо перейти к анализу со-

ответствующих тенденций в процессе и затем, после выделения этих изме-

нений - к началу схемы.

В случае, если реализация не может быть отнесена к нормальным, не-

обходимо, как уже говорилось выше, выдвигать гипотезы о других теоре-

тических распределениях и проверять их до тех пор, пока не будет получе-

но достаточно точное решение. При этом точность определяется уровнем

значимости в критерии Х

-квадрат [20].

На этом этапе анализ отдельной реализации заканчивается и его сле-

дует применять ко всем имеющимся реализациям. (Заметим, что многие из

операций этого этапа могут быть реализованы на компьютере, для чего

имеются специальные программы).

Имитационное моделирование

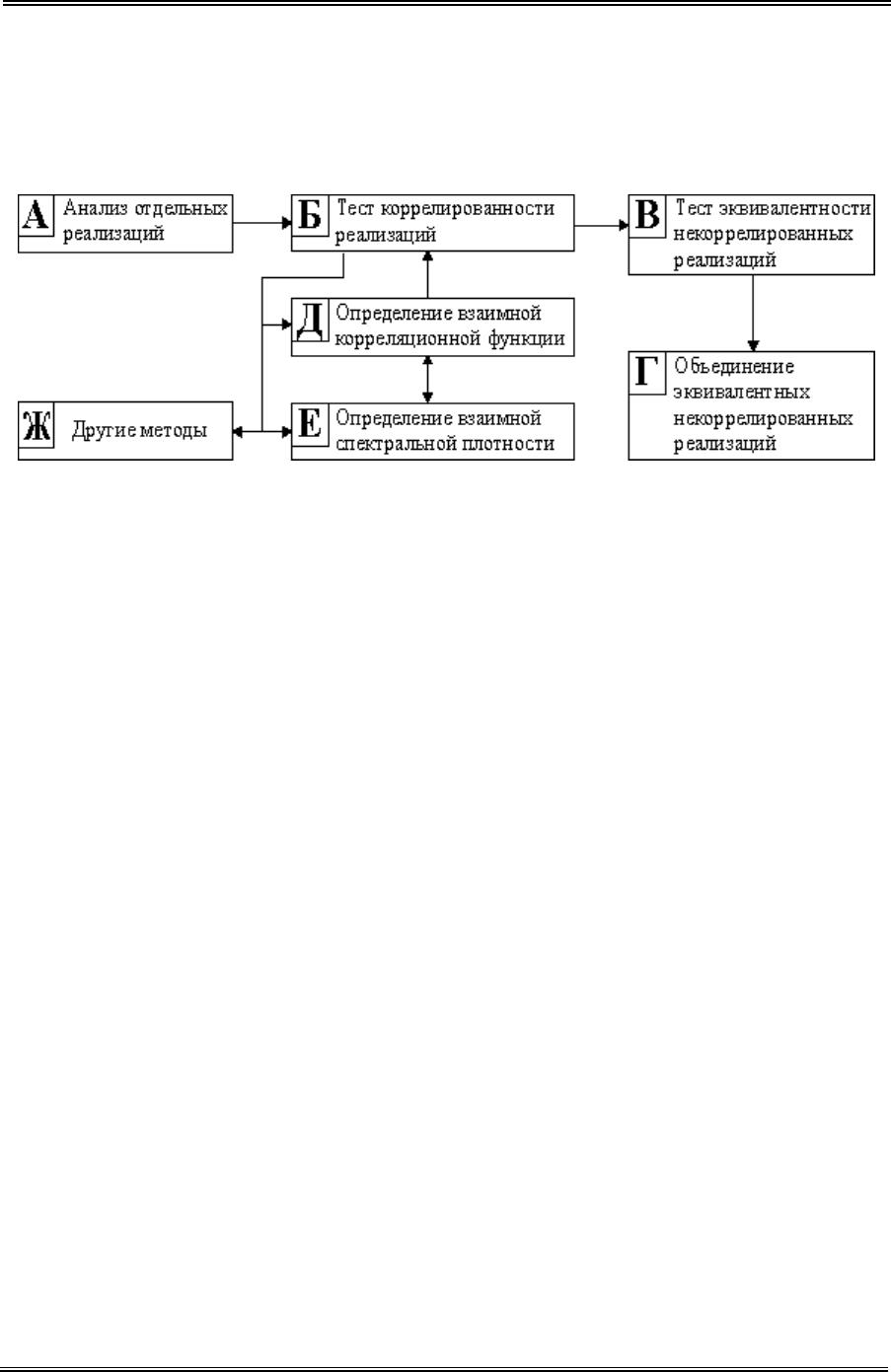
Следующим этапом исследования реализации является анализ сово-

купности реализаций (рис. 4.5).

Рис. 4.5. Анализ совокупности реализаций.

Этот анализ начинается с проведения теста коррелированности реали-

заций. Суть его состоит в том, чтобы по оценкам взаимных корреляцион-

ных функций (или взаимных спектральных плотностей) с помощью стати-

стических критериев о значимости коэффициентов корреляции [20], ре-

шить в количественной форме с указанием точности, являются ли реализа-

ции статистически связанными.

Если реализации коррелированы, то этап анализа совокупности реали-

заций на этом заканчивается. В противном случае необходимо попытаться

установить их эквивалентность. Для этого реализуется тест эквивалентно-

сти. Основной его смысл состоит в выявлении эквивалентных по вероятно-

стным свойствам реализаций случайного процесса. При проведении этого

теста используются статистические критерии об эквивалентности реализа-

ций (выборок) [20]. В случае обнаружения таких реализаций и в случае,

если для моделирования безразлично, какие из процессов, порождающих

эти реализации, необходимо использовать, эквивалентные реализации объ-

единяются. При этом основным критерием объединения является предста-

вительность реализации в смысле полноты описываемых свойств процесса

и длины реализации.

Таким образом, после проведения статистического анализа исследова-

тель располагает сведениями, достаточными для выбора метода воспроиз-

ведения того или иного процесса. Естественно, что вопрос о том, воспро-

изводить ли реализацию каким-либо методом генерирования или исполь-

зовать реальные ряды наблюдений (если их достаточное количество), ре-

шается исходя из целей моделирования и наличия достаточных объемов

данных. Если принимается решение об использовании реальных данных,

то вопроса о выборе метода генерирования не возникает. Но это, как пра-

вило, весьма и весьма редкий случай. Имитация, как статистический ме-

Имитационное моделирование

тод, требует многократных повторений численных экспериментов (для ус-

реднения результатов) и, естественно, что необходимо использовать раз-

личные, но эквивалентные по вероятностным свойствам, реализации слу-

чайных процессов. А это возможно только с помощью методов генериро-

вания.

4.2.2. Методы воспроизведения входных воздействий.

Исследование объектов и систем управления ими с помощью имита-

ционного моделирования и стремление достичь определенного уровня

адекватности модели реальному объекту заставляют непрерывно совер-

шенствовать и развивать методы и устройства моделирования случайных

процессов с разнообразными вероятностными свойствами. При этом ис-

следователь может обладать либо общими представлениями о свойствах

моделируемого процесса, которые получены в результате анализа реализа-

ций и которые требуется воспроизвести, либо имеет реализации процессов,

которые необходимо увеличить в объеме с сохранением вероятностно-

статистических свойств исходных реализаций. В первом случае речь идет

о генерировании случайных процессов, во втором - об их имитации.

Имитация случайных процессов, кроме применения в моделировании,

позволяет существенно сокращать объемы собираемых данных. В подав-

ляющем числе случаев отбор наблюдений является трудоемким и дорого-

стоящим процессом. Отсюда очевидным является стремление снизить ко-

личество проб, получив при этом максимально возможные сведения об ис-

следуемом случайном процессе.

Одним из возможных путей решения этой задачи является искусст-

венное увеличение объема некоторой исходной, небольшой по объему

реализации с тем, чтобы более ясно и четко выделить интересующие нас

вероятностные свойства.

Практические задачи, использующие статистическую информацию и

решаемые подобным образом, могут быть разделены на три класса:

1) реализующие только знания о законах распределения вероятно-

стей;

2) использующие только сведения о динамических (корреляционных,

спектральных и других) свойствах информации;

3) использующие данные одновременно о законах распределения

вероятностей и динамических свойствах.

Задачи первого класса могут быть решены простым и известным пу-

тем [37]: исходная информация помещается в некоторый бункер (урну) и

затем каждое из значений наугад вынимается и после фиксации вновь воз-

Имитационное моделирование

вращается в урну. Это классический пример снятия каких-либо динамиче-

ских связей. Причем при достаточно большом числе извлечений одномер-

ный закон распределения получаемой реализации стремится к одномерно-

му закону распределения исходной реализации.

С целью сохранения динамических свойств (нарушая при этом полно-

стью или частично одномерный закон распределения вероятностей) может

быть использована процедура, связанная с многократным повторением ис-

ходной реализации. При этом, если исходная реализация повторяется пол-

ностью, то имеет место сохранение одномерного закона распределения ве-

роятностей. Динамические свойства в выходной реализации будут иметь

ярко выраженный период, равный длине переносимого отрезка, то есть

числу извлекаемых подряд без изменения порядка следования значений

исходной реализации. Подобная процедура описана в работе [37].

С целью более полного использования вероятностно-статистических

свойств случайных процессов по выборкам малой длины (третий класс за-

дач) может быть применена одна из процедур генерирования случайных

процессов с заданным законом распределения вероятностей и корреляци-

онными свойствами. Для этого, пользуясь выше рассмотренными метода-

ми, получают максимально возможные сведения о вероятностных свойст-

вах случайного процесса (отдельно - о законе распределения вероятностей

и отдельно - о корреляционных свойствах). Затем, используя соответст-

вующие процедуры генерирования, воспроизводят реализации с требуе-

мыми динамическими и статическими свойствами.

Очевидно, что на имеющемся уровне знаний об исходном процессе

исследователь вынужден считать исходную реализацию представительной.

Статистические свойства полученной реализации обладают некоторой

ошибкой в сравнении с исходными, но при малых длинах исходных реали-

заций мы получаем возможность использовать эти значения для различных

работ.

Вместе с тем, использование методов генерирования, а не имитации

случайных процессов, предпочтительнее, так как эти методы более техно-

логичны в использовании из-за возможностей управления параметрами за-

конов распределения вероятностей и корреляцией (чего нет в имитации).

4.2.2.1. Классификация методов генерирования

и имитации входных воздействий.

Исследуя объект и систему управления им с помощью имитационного

моделирования и стремясь достичь определенного уровня адекватности,

необходимо использовать алгоритмы формирования и преобразования

случайных событий, величин, процессов и полей.

Имитационное моделирование

Под методами генерирования и имитации понимаются физически ли-

бо алгоритмически реализованные процедуры, позволяющие получать

дискретные или непрерывные процессы, которые по своей природе явля-

ются случайными (или псевдослучайными при наличии некоторых допу-

щений относительно природы генерируемого процесса [12,18,19,35,40].

Здесь и далее будем называть случайностью набор случайных или псевдо-

случайных чисел, который в зависимости от требований исследования

можно рассматривать как множество реализаций одномерной или много-

мерной случайной величины, либо в качестве реализации одномерного или

многомерного случайного процесса, либо в качестве реализации случайно-

го поля.

В том случае, когда речь идет об имитации проектируемой, а иногда и

эксплуатирующейся системы исследователь обладает лишь более или ме-

нее точными сведениями о свойствах входных процессов и должен при-

бегнуть к использованию методов генерирования случайных процессов как

средству имитации функционирования элементов системы.

Таким образом, основным средством воспроизведения входных воз-

действий являются методы генерирования случайных процессов с задан-

ными статистическими свойствами. В связи с этим, в дальнейшем под ге-

нераторами понимаются такие методы воспроизведения случайных про-

цессов, которые воспроизводят случайность с заданными исследователем

из каких-либо гипотетических соображений статистическими свойствами.

А под имитаторами понимаются методы воспроизведения случайных про-

цессов с требуемыми статистическими свойствами, основанные на исполь-

зовании реальных данных.

Использование понятия случайности неразрывно связано с ее вероят-

ностными характеристиками, которые можно разделить на две группы. К

первой группе (наиболее крупной) отнесем статистические характеристики

- закон распределения вероятностей и, следовательно, функцию распреде-

ления и, при существовании, плотность распределения вероятностей и то-

му подобное, то есть такие характеристики, которые отражают вероятно-

стные свойства каждой реализации независимо от степени взаимовлияния

и взаимосвязанности реализаций. Вторую группу составляют характери-

стики, отражающие динамические свойства, то есть корреляционные

функции и моменты, структурные функции, спектральные функции и тому

подобное.

Проблема создания источников случайности может быть решена дву-

мя путями:

1) созданием источников, доставляющих исследователю случай-

ность, обладающую требуемыми статическими и (или) динамическими

свойствами;

Имитационное моделирование

2) созданием источников первичной случайности, насчитывающих

весьма ограниченное число разновидностей, и разработкой различных ме-

тодов ее преобразования для получения заданных свойств.

Необходимость создания физической (или алгоритмической) проце-

дуры, адекватно воспроизводящей те или иные реальные явления, порож-

дающие вполне определенные вероятностные свойства генерируемой слу-

чайности, приводит ко вполне понятным трудностям в реализации первого

способа.

В подавляющем большинстве предпринятых реализаций второго спо-

соба в качестве первичной случайности, которая в дальнейшем подверга-

ется каким-либо преобразованиям, выбираются случайные или псевдослу-

чайные числа X, имеющие равномерный в интервале [0,1] закон распреде-

ления вероятностей и являющиеся независимыми между собой. Несколько

реже в качестве исходной величины используют случайную цифру X', ко-

торая с вероятностью p=0,1 может принимать любое из десяти значений:

0,1,2,3,4,5,6,7,8,9.

В [12,18,19,35,40] подробно рассмотрены принципы построения гене-

раторов первичной случайности, освещены преимущества и недостатки

многих из них. В связи с тем, что основой имитации служат различные по

своим свойствам случайные величины, процессы и поля, основное внима-

ние в данной главе уделяется методам преобразования вероятностных

свойств и предполагается, что в распоряжении исследователя имеется ге-

нератор первичной случайности, позволяющий получать наборы чисел с

равномерным законом распределения вероятностей в интервале [0,1].

Методы преобразования первичной случайности могут быть класси-

фицированы по конечным целям преобразований на Р-, R- и РR-методы

[43]. По способам воплощения эти же методы могут быть разделены на

физические устройства и алгоритмические процедуры. Простота и деше-

визна реализации последних обусловили их преимущественное использо-

вание в имитационном моделировании. В связи с этим в данной главе рас-

сматриваются только алгоритмические преобразования случайности.

Под Р-методами понимаются процедуры для получения некоррели-

рованных наборов случайных (или псевдослучайных) чисел, обладающих

требуемым законом распределения вероятностей.

R-методы - это процедуры, позволяющие генерировать наборы слу-

чайных чисел с требуемыми динамическими свойствами и произвольным

(безразличным для исследователя) законом распределения вероятностей.

РR-методами будем называть такие преобразования первичной слу-

чайности, которые наряду с требуемыми статистическими свойствами по-

зволяют получать необходимые динамические свойства в генерируемых

наборах случайных или псевдослучайных чисел.

Имитационное моделирование

Рассмотренная выше классификация методов преобразования случай-

ности в зависимости от соотношения статических и динамических свойств

обуславливается теми задачами, для которых, собственно, и создаются эти

методы. Для ряда задач, требующих только знания статических свойств

воспроизводимой случайности, выделены Р-методы. В других задачах

важно воспроизвести корреляционные или иные динамические свойства, а

на статику не накладывается никаких жестких ограничений. Наконец, су-

ществует ряд задач, в которых необходимо по возможности точно воспро-

извести статические и динамические свойства генерируемой случайности.

Очевидно, стремясь достичь определенной степени адекватности модели и

реального объекта, необходимо использовать и соответствующий класс

методов воспроизведения случайности. Причем, сравнительно редкое при-

менение R-методов и тем более РR-методов объясняется скорее сложно-

стью этих методов, чем стремлением к упрощению моделей.

Рассматривая имеющиеся в литературе методы введения требуемых

динамических свойств, следует отметить их узкую направленность на по-

лучение стационарных случайных процессов и полей с заданной корреля-

ционной зависимостью и в связи со свойством стационарности, заданной

структурной зависимостью. Имитационное моделирование сложных сис-

тем, несомненно, требует создания специальных динамических и комби-

нированных методов преобразования случайности, позволяющих получать

требуемые частотные и структурные зависимости и для нестационарного

генерируемого процесса или случайного поля. Это обусловлено теми осо-

бенностями указанных характеристик, которые позволяют более тонко и

точно имитировать реальные физические процессы и явления.

4.2.2.2. Источники первичной случайности.

В качестве первичных случайных чисел, которые в дальнейшем под-

вергаются каким-либо преобразованиям, выбирают некоррелированные

реализации ξ

случайной величины ξ, обладающей равномерным в интер-

вале [0,1] одномерным распределением вероятностей. Реже в качестве пер-

вичных случайных чисел используются реализации η

, случайной дискрет-

ной величины η, которая с равной вероятностью 1/10 принимает значения

0, 1, 2, 3, 4, 6, 5, 7, 8, 9. В дальнейшем в этом параграфе ξ

будем называть

случайным числом, а величину η

- случайной цифрой. Для установления

связи между ξ

и η

, разложим число ξ

в бесконечную десятичную дробь:

= 0,η

,η

, …, η

, … (4.1)

Имитационное моделирование

100

Эта запись означает, что

∑

∞

−

⋅η

В [40] доказана теорема о независимости случайных цифр в случай-

ном числе, которая формулируется следующим образом.

Десятичные цифры η

,η

, …,η

, … случайного числа ξ

представляют

собой независимые случайные цифры. Обратно, если η

,η

, …, η

, … - не-

зависимые случайных цифры, то формула (4.1) дает случайное число.

В вычислительных процессах всегда используют числа с конечным

количеством десятичных знаков, поэтому вместо случайных чисел ξ

упот-

ребляют конечные десятичные дроби ξ

=0, η

,η

, …, η

. Принято считать,

что здесь имеют место ошибки округления.

Предположим, что, используя некоторый механизм (игральную кость,

рулетку и т.п.), мы осуществили ряд опытов, в результате которых получи-

ли Ν случайных цифр, η

,η

, …, η

. Записав эти цифры в таблицу, полу-

чим то, что называется таблицей случайных цифр (приложение 2). Это есть

первый способ получения первичных случайных чисел.

Способ употребления такой таблицы прост. Если в ходе решения не-

которой задачи нам потребуется случайная цифра η

, то мы можем взять

любую цифру η

из этой таблицы. Если нам потребуется случайное число

, то мы можем по произвольному алгоритму выбрать из таблицы n оче-

редных цифр и считать, что

= 0, η

, …, η

Еще раз отметим произвольность выбора алгоритма получения цифр из

таблицы, не зависящего от конкретных значений этих цифр.

Пример 4.1. Используя таблицу (см. приложение 2) равномерно рас-

пределенных случайных цифр, получить пять случайных цифр.

Решение 4.1.а. Выбираем наугад строку таблицы. Пусть это будет 5-я

строка. Выписываем из нее 5 цифр: 1,2,8,0,7.

Решение 4.1.б. Выбираем наугад строку и колонку и, начиная с вы-

бранной цифры, двигаемся по диагонали влево и вверх по таблице.

Пусть мы выбрали 9-ю строку и 10-ю колонку. Тогда получаем сле-

дующие цифры: 5, 0, 8, 4, 9.

Пример 4.2. Используя таблицу равномерно распределенных случай-

ных цифр, получите четыре случайных трехзначных числа.

Решение 4.2.а. Выбираем наугад колонку и выписываем из нее, двига-

ясь вниз, 12 цифр. Пусть мы выберем, первую колонку и тогда получим

цифры: 1,3,0,9,1,6,3,8,6,7,9,1. Сгруппируем их в четыре группы (заметим,

что это можно сделать по-разному): 130, 916, 386, 791.

Решение 4.2.б. Воспользовавшись ходом шахматного коня и начиная с