Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.


81
x
n
X
n
2
sin
π
= ,
N
n∈ .
Заметим, что 0≠n (почему?).
Рассмотрим уравнение
0
4
9
=+
′′
TT
n
λ
.
Имеем
tBtAT
nnnnn
λλ
2
3
sin
2
3
cos += .
Тогда
)()(),( tTxXtxu
nnn
=
и решение задачи имеет вид
∞
=
=
1
),(),(
n
n
txutxu ,
или, в развернутом виде, -
∞
=
+=
1
2
sin)
4
3
sin
4
3
cos(
n
nn
x
n
t
n
Bt
n
Au
πππ
.
Используем начальные условия. Имеем
==
−==
∞
=
∞
=
1
1
0
2
sin
4
3
)0,(
)2(
2
sin)0,(
n
nt
n
n
x
nn
Bxu
xxx
n
Axu
ππ
π
.
Отсюда
=
−=
0
2
sin)2(
2
sin
2
0
2
0
2
n
n
B
xdx
n
xxxdx
n
A
ππ
Интегрируя по частям, имеем
)1(cos
)(
16
3
−= n
n
A
n
π
π
или

82
)1)1((
)(
16
3
−−=
n
n
n
A
π
или
=
+=
−
=
mn
mn
nA
n
2 ,0
12 ,
)(
32
3
π
Таким образом, окончательно решение задачи имеет вид
x
m
t
m
m
txu
m
2
)12(
sin
4
)12(3
cos
)12(
132
),(
0
33
+
⋅
+
+
−=
∞
=
ππ
π
.
Лекция 7. Метод Фурье: продолжение (применительно к решению
простейших многомерных задач)
Продемонстрируем применение метода на примере отдельных типовых
задач.
7.1. Гиперболическая задача (в прямоугольной области)
Задание. Решить первую смешанную задачу для волнового уравнения в
прямоугольнике:
uu
tt
Δ⋅= 49
(1)
=
=
−−=
=
0
0
)2)(7(
0
t
u
yxxy
t
u
t
(2)
0
2700
=
=
=
=
=
=
=
= y
u
x
u
y
u
x
u
. (3)
Решение. Здесь
yyxx
uuu +=Δ . В данном случае область )},{( y
x
представляет собой прямоугольник ]2,0;7,0[=D .

83
Согласно общей схемы (см. Лекция 6) решение задачи (1) – (3) ищем в
виде
)(),(),,(
t
T
y
x
Ф
t
y
x
u ⋅= .
Подставим ),,(
t
y
x
u в уравнение (1), получим
T
Ф
T
Ф ⋅Δ⋅=
′′
49 ,
или, после разделения переменных,
)0(
49
≥−=
Δ
=
′′
λλ
Ф
Ф
T
T
.
Отсюда
=+Δ
=+
′′
0
049
ФФ
TT
λ
λ
. (4)
Рассмотрим вначале второе из уравнений (4). Положим
)()(),( y
Y
x
Xy
x
Ф = .
Тогда, подставив это выражение, и, разделив переменные, получим
λ
−=
′′
+
′′
Y
Y
X
X
.
Обозначим, теперь, слагаемые левой части через
μ
− ,
ν
−
соответственно,
μ
−=
′′
X
X
, (5)
ν
−=
′′
Y
Y
, (6)
тогда
λ
ν
μ
=+ . (7)
Из граничных условий (3) следует, что
0)7()0( == XX , (8)
0)2()0( ==
Y
Y
. (9)
Из опыта решения одномерных задач (см. лекция 5) известно, что
0, ≥
ν
μ
. Решая задачу (5), (8) имеем

84
x
n
X
n
7
sin
π
= ,
2
7
=
n
n
π
μ
,
N
n∈
задачу (6), (9), -
y
m
Y
m
2
sin
π
= ,
2
2
=
m
m
π
ν
,
N
m∈ .
Таким образом, система собственных функций исходной краевой
задачи имеет вид
y
m
x
n
yYxXФ
mnnm
2
sin
7
sin)()(
π
π
⋅== , (10)
система собственных значений, -
22
27
+
=+=
mn
mnnm
ππ
νμλ
,
N
mn ∈, . (11)
Вернёмся к нахождению функций )(
t
T
. Рассмотрим первое из
уравнений (4). Имеем
049 =+
″
nmnmnm
TT
λ
,
тогда
)7sin()7cos( tBtAT
nmnmnmnmnm
λ
λ
+= . (12)
Таким образом, существуют двупараметрическое семейство функций
nmnmmm
TФu = , удовлетворяющих уравнению (1) и граничным условиям (3).
Решение задачи (1)-(3) ищем теперь в виде
∞
=
=
1,
)(),(),,(
mn
nmnm
tTyxФtyxu . (13)
Используем начальные условия (2). При 0=
t
из (13) с учётом (10), (12)
имеем
−−=⋅⋅
mn
nm
yxxyy
m
x
n
A
,
)2)(7(
2
sin
7
sin
π
π
, (14)
=⋅⋅
mn
nm
y
m
x
n
B
,
0
2
sin
7
sin
π
π
. (15)

85
Из (15) следует, что 0=
nm
B . Коэффициенты
nm
A определяются из (14)
обычным образом: обе части умножаются на
),( yxФ
nm
и почленно
интегрируются по области
D
. В результате, имеем
−−=
DD
nmnmnm
dxdyФyxxydxdyyxФA )2)(7(),(
2
,
т.е.
dy
m
yyxdx
n
xxA
nm
2
sin)2(
7
sin)7(
7
2
7
0
2
0
ππ
−
⋅−= ,
откуда, после раздельного вычисления каждого из интегралов по частям,
+=+=
⋅⋅
⋅
==
=
12 ,12 если ,
72
2 или ,2 если ,0
11
336
28
11
mmnn
mn
nmnn
A
nm
π
.
Таким образом, окончательно
=),,(
t
y
x
u
+
⋅
+
++
⋅
=
∞
=
++
0,
12,12
33
6
2
)12(
sin
7
)12(
sin)7cos(
)12()12(
12
196
mn
mn
y
m
x
n
t
mn
ππ
λ
π
,
где
12,12 ++ mn
λ
описывается соотношением (11).
7.2. Параболическая задача (в круговой области)
Задание. Найти решение первой смешанной задачи для уравнения
теплопроводности
uu
t
Δ⋅= 7, 40 ≤≤
r
, 0>
t
(16)
2
16)0,( rru −= , (17)
0),4( =
t
u . (18)
Решение. Если учесть однородность уравнения, а также зависимость
начальных и граничных условий только от расстояния
r
точки от начала
координат и конфигурацию области, можно прийти к заключении о наличии
в решении задачи осевой симметрии. Таким образом, процесс в физически
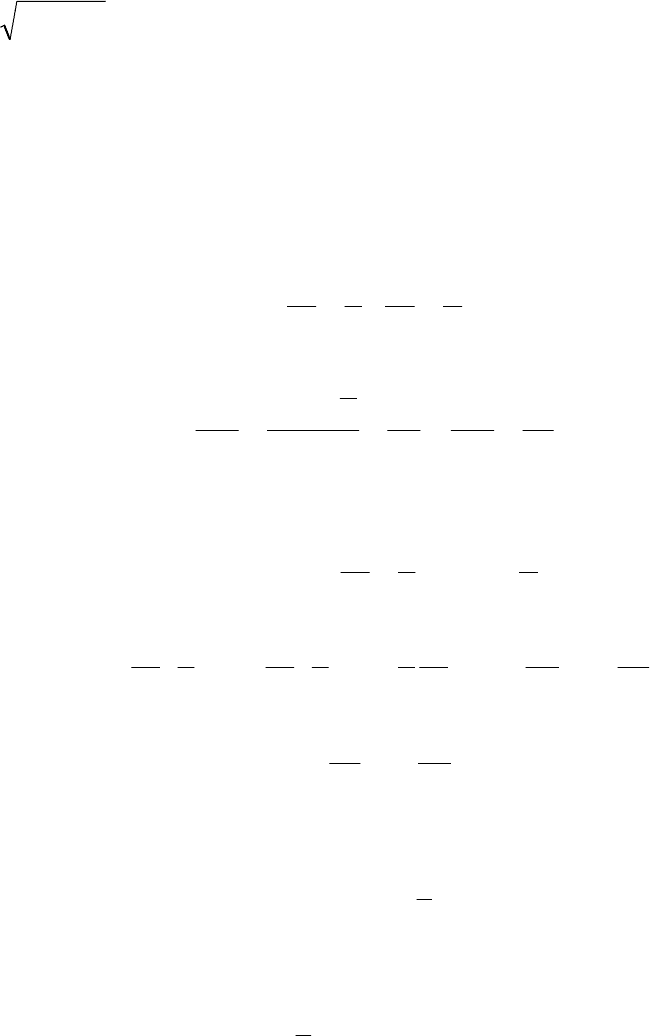
86
двумерной области математически описывается одномерным уравнением.
Т.е.
),(
t
r
uu = ,
где
22
yxr +=
.
Представим оператор Лапласа uΔ в полярных координат с самого
начала предполагая отсутствие зависимости функции u от
ϕ
, т.е. считая
0≡
ϕ
u .
Имеем
r
x
x
r
=
∂
∂
,
r
y
y
r
=
∂
∂
,
3
2
22
2
r
y
r
r
x
xr
x
r
=
⋅−
=
∂
∂
,
3
2
2
2
r
x
y
r
=
∂
∂
.
Тогда
rrx
u
r
x
x
r
uu =
∂
∂
= ,
ry
u
r
y
u =
,
rrrrrrxx
u
r
x
u
r
y
u
xr
x
u
r
x
x
u
r
x
x
u
2
2
3
2
)( +=
∂
∂
+
∂
∂
=
∂
∂
= ,
rrryy
u
r
y
u
r
x
u
2
2
3
2
+= ,
и
rrryyxx
uu
r
uuu +=+=Δ
1
.
В результате уравнение (16) принимает вид
+=
rrrt
u
r
uu
1
7, 40 <≤
r
, 0>
t
. (16
1
)
Решение задачи (16
1
), (17), (18) ищем в виде
)()(),(
t
T
r
R
t
r
u ⋅= . (19)
Подставляя (19) в (16
1
) и разделяя переменные, получим

87
λ
−=
′
+
′′
=
′
R
R
r
R
T
T
1
7
)0( ≥
λ
,
откуда
07 =+
′
T
T
λ
(20)
и
0
1
=+
′
+
′′
RR
r
R
λ
. (21)
Определимся с граничными условиями для функции )(
r
R
. Из (18), в
частности, следует, что
0)4( =
R
. (22)
Учтём, далее, что уравнение (21), - второго порядка. Поэтому, в
качестве второго дополнительного условия потребуем ограниченность
функции
R
в окрестности точки 0=
r
, т.е.
∞<± )0(R . (23)
Заметим, что данное требование вполне соответствует физическим
представлениям (ведь рассматриваемая задача вполне может описывать
процессы теплообмена или диффузии), с другой стороны, - оно оказывается и
математически достаточным для однозначного определения набора
собственных функций краевой задачи.
Рассмотрим уравнение (21). Умножив его обе части на
2
r
, получим
уравнение
0
22
=+
′
+
′′
R
r
R
r
R
r
λ
, (24)
которое является частным случаем
уравнения Бесселя. Для дальнейшего
необходимо ознакомление с некоторыми свойствами этого уравнения. Они
изложены ниже в замечании.
Замечание. (О теории решения уравнения Бесселя).
Дифференциальное уравнение второго порядка
0)()()()(
222
=−+
′
+
′′
zRzzRzzRz
ν
, (25)

88
где
2
ν
- постоянная, называемая уравнением Бесселя. Если в уравнении (24)
сделать замену
zr =
λ
, то получим уравнение (25) при 0=
ν
. Ненулевые
решения уравнения (25) называются
цилиндрическими функциями, они
строятся в виде степенных рядов. Одно из таких решений называется
функцией Бесселя, обозначается символом )(zI
ν
и имеет вид
+⋅++
−
=
∞
=
+
0
2
)1()1(
)2/()1(
)(
k
kk
kГkГ
z
zI
ν
ν
ν
,
где
⋅=
+∞
−−
0
1
)( dttezГ
zt
и называется
гамма-функцией. Свойства функции )(zГ хорошо изучены,
вот некоторые из них:
1. для 0>z )()1( zzГzГ =+ ;
2. для 0≤z ∞=)(zГ ;
3. !)1( nnГ =+ ;
4. )(zГ не имеет вещественных нулей.
В силу этих свойств функция Бесселя при
N
n∈ , в частности, имеет вид
+
−
=
∞
=
+
0
2
)!(!
)2/()1(
)(
k
nkk
n
knk
z
zI
.
Так как степень параметра
ν
в уравнении (25) чётна, то, очевидно,
)(zI
ν
−
также является его решением. Если
ν
- нецелое, то функции )(zI
ν
и
)(zI
ν
−
линейно независимы и общее решение уравнения (25) имеет вид
)()()(
21
zICzICzR
νν
−
+= .
Если же
N
n∈=
ν
, то
)()1()( zIzI
n
n
n
−=
−
,
т.е. функции
)(zI
n
и )(zI
n−
линейно зависимы. Поэтому для описания
общего решения уравнения Бесселя, в этом случае, используют
функцию
Неймана
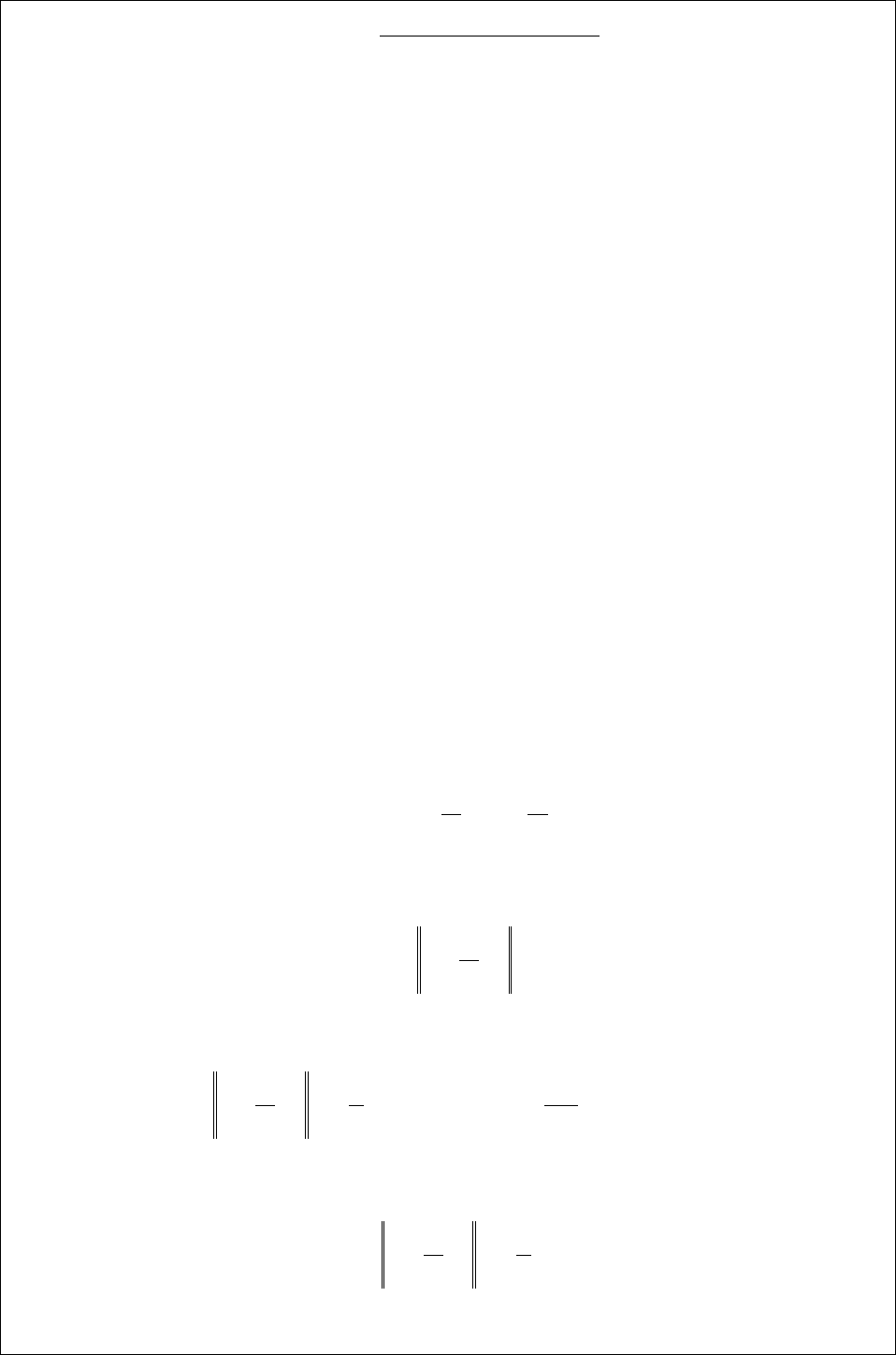
89
νπ
νπ
νν
ν
sin
)(cos)(
)(
zIzI
zN
−
−
= ,
которая для целых значений n определяется с помощью предельного
перехода
)(lim)( zNzN
n
n
ν
ν
→
=
.
Функция Неймана также является решением уравнения Бесселя и
линейно независима с )(zN
ν
. Поэтому общее решение уравнения (25), в этом
случае, можно представить в виде
)()()(
21
zNCzICzR
nn
+= . (26)
Однако функция )(zN
n
в окрестности точки 0=z является
неограниченной, поэтому ограниченные решения уравнения (25) имеют вид
)()(
1
zICzR
n
= .
Далее, функции Бесселя обладают своеобразными свойствами
ортогональности. А именно, пусть
β
α
, - корни одного из уравнений
0)( =zI
ν
, 0)( =
′
zI
ν
, 0)()( =+
′
zhIzzI
νν
. (27)
Тогда для 1−>
ν
справедливо
0
0
=
dzz
l
Iz
l
zI
l
βα
νν
, (28)
т.е. функции Бесселя ортогональны с весом
z
. Если же
β
α
=
, то (28)
представляет собой квадрат нормы
2
z
l
I
α
ν
функции Бесселя. В частности,
показано, что
−+
′
=
)(1)(
2
2
2
2
2
2
2
α
α
ν
α
α
ννν
II
l
z
l
I .
Отсюда, в частности, для первого из уравнений (27) имеем
)(
2
2
2
2
α
α
νν
′
=
I
l
z
l
I , (29)
Для второго, -

90
)(1
2
2
2
2
2
2
α
α
να
νν
I
l
z
l
I
−=
.
Нули цилиндрических функций.
При 0≥
ν
нули
μ
цилиндрических функций изолированы,
вещественны, их бесконечно много и положительные из них можно
пронумеровать в порядке возрастания натуральными числами, т.е.
......0
21
<<<<<
n
μ
μ
μ
.
Таким образом, набор функций
z
l
I
n
μ
ν
образует ортогональную, с
весом
z
, систему функций, которая оказывается и полна на отрезке ];0[
l
.
Вернёмся к уравнению (24).
В данном случае значение 0=
ν
, поэтому его общее решение, с учётом
замены
λ
rz = , согласно (26), имеет вид
)()()(
0201
λλ
rNCrICrR += .
Однако, в силу неограниченности функции Неймана и требования (23),
имеем
)()(
01
λ
rICrR = .
Далее, из граничного условия (22) следует, что
0)4()4(
01
==
λ
ICR
.
Пусть
n
μ
- положительные корни уравнения 0)(
0
=
μ
I . Тогда набор
16
2
n
n
μ
λ
= ,
N
n∈
представляет собой систему собственных значений, а набор функций
= rIrR
n
n
4
)(
0
μ
,
- систему собственных функций исходной краевой задачи.
Перейдем теперь к уравнению (20). Имеем
