Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.

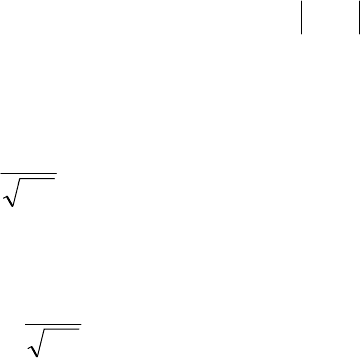
101
xxt
uau
2
= , +∞<<∞−
x
,
0>
t
(7)
)()0,(
x
x
u
ϕ
= .
Для неё функция Грина вводится аналогичным образом, а именно, - как
решение задачи
xxt
vav
2
= , +∞<<∞−
x
,
0>t
(8)
)()0,(
ξ
δ
−=
x
x
v
. (8
1
)
Обозначим его также через ),,(
t
x
G
ξ
. Тогда решение задачи (7) будет
иметь вид
+∞
∞−
=
ξξϕξ
dtxGtxu )().,(),( (7
1
)
Изложим порядок нахождения функции ),,(
t
x
G
ξ
. В силу отсутствия
граничных условий, метод Фурье непосредственно неприменим. В данном
случае используются идеи, лежащие в основе операционного исчисления. А
именно, применение к решаемому уравнению преобразования Фурье
позволяет понизить размерность задачи и свести решение уравнения в
частных производных к решению обыкновенного дифференциального
уравнения.
Напомним некоторые особенности преобразования Фурье.
Пусть непрерывно
дифференцируемая функция )(
x
f
абсолютно
интегрируема на числовой оси, т.е.
+∞
∞−
∞<dxxf )(. Тогда её
преобразованием Фурье
[]
)(xfℑ
называется следующий интеграл
[]
)()(
2
1
)( wFdxexfxf
iwx
==ℑ
+∞
∞−
−
π
, (9)
причем
+∞
∞−
= dwewFxf
iwx
)(
2
1
)(
π
. (10)

102
Соотношение (9) называется еще прямым преобразованием Фурье, а
соотношение (10), -
обратным. Помимо линейных свойств для
преобразования Фурье справедлива, так называемая,
теорема
дифференцирования
:
[
]
[]
)()()(
)(
xfiwxf
nn
ℑ⋅=ℑ .
Т.е.
+∞
∞−
−
= )()()(
2
1
)(
wFiwdxexf
niwxn
π
.
Применим теперь преобразование Фурье к задаче (8). Умножая обе
части её уравнения на
iwx
e
−
π
2
1
и интегрируя по
x
на интервале ),( +∞−∞ ,
имеем
),(),(
22
twFwatwF
t
−=
, (11)
где
+∞
∞−
−
= dxetxvtwF
iwx
),(
2
1
),(
π
.
А из граничного условия (8
1
) имеем
dxexwF
iwx−
+∞
∞−
−= )(
2
1
)0,(
ξδ
π
,
т.е.
ξ
π
iw
ewF
−
=
2
1
)0,(
(12)
Соотношения (11), (12) представляют собой уже задачу Коши для
обыкновенного дифференциального уравнения, величина w в нём играет
роль параметра. Общее решение уравнения (11) имеет вид
twa
eCF
22
0
−
= ,
а из начального условия (12) определяем
ξ
π
iw
eC
−
=
2
1
0
.

103
Таким образом, решение задачи (11), (12) и, тем самым,
преобразование Фурье искомой функции
v
, т.е. решения задачи (8), (8
1
),
имеет вид
)(
22
2
1
ξ
π
vwtwa
eF
+−
=
.
Найдем функцию
v
, используя некоторые сведения из теории
преобразований Фурье, а именно, - теорему сдвига и таблицу
преобразований. Первая из них утверждает:
если
[]
)()( wCxf =ℑ
, то
[]
)()( wCexf
iw
ξ
ξ
=+ℑ .
Положим в нашем случае
twa
ewC
22
2
1
)(
−
=
π
.
Тогда ),(
t
x
v
, - результат применения обратного преобразования Фурье
к функции )(w
C
. Согласно таблице преобразований:
если
pw
e
p
wC
4/
1
2
2
1
)(
−
= , то
2
)(
px
exf
−
= , 0Re >
p
.
В нашем случае следует считать, что
t
a
p
2
4
1
= . Тогда
)(
2
1
)(
1
4/
2
wC
p
e
p
p
wC
pw
⋅=⋅=
−
ππ
и, с учётом линейности преобразования,
2
)(
px
e
p
xf
−
=
π
,
т.е.
ta
x
e
ta
xf
2
2
4
2
4
1
)(
−
=
π
.
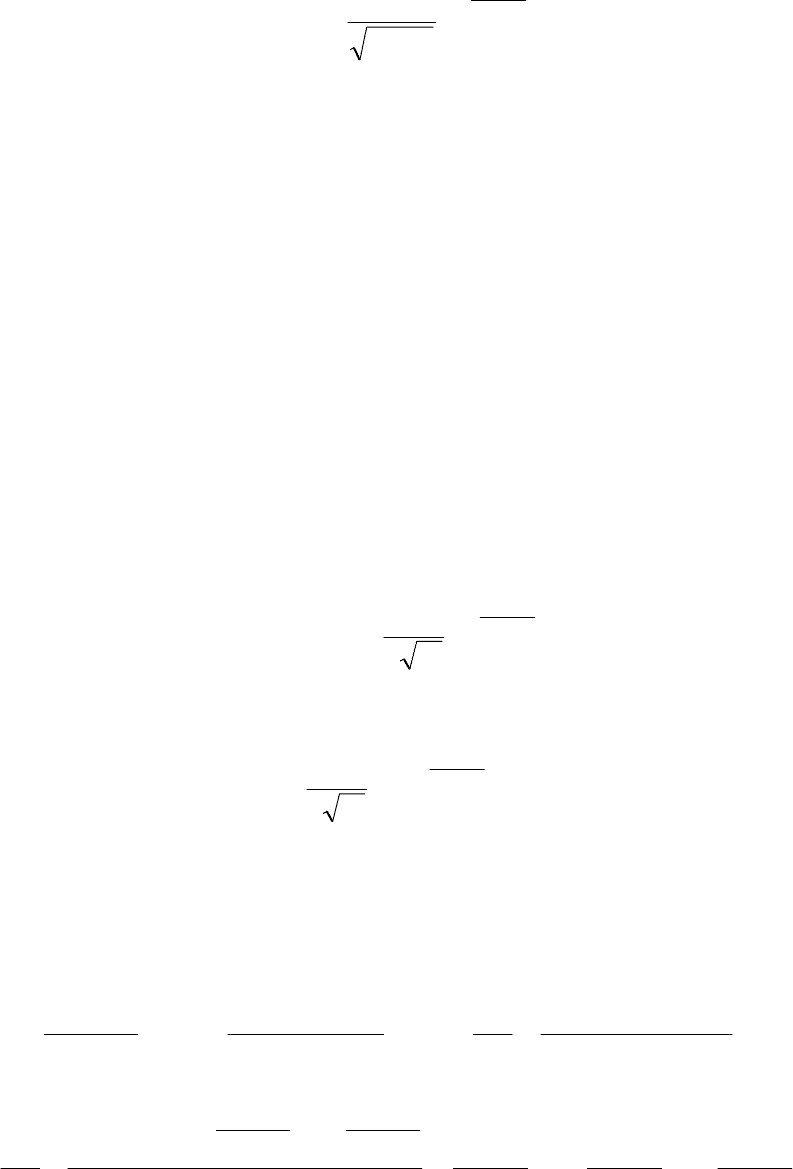
104
Тогда с учётом сдвига, функция )(
ξ
−
x
f
, т.е. ),(
t
x
v
и, тем самым
),,(
t
x
G
ξ
, имеет вид
ta
x
e
ta
txG
2
2
4
)(
2
4
1
),,(
ξ
π
ξ
−
−
= . (13)
Это и есть функция Грина задачи Коши (7).
8.3. Пример
Рассмотрим следующую задачу
txx
uu =9,
2
)0,(
x
exu
−
= , +∞<<∞−
x
, 0>
t
.
Она имеет вид (7), следовательно, её решение, - вид (7
1
). Т.е.
+∞
∞−
−
=
ξξ
ξ
detxGtxu
2
),,(),(.
В данном случае, согласно (13), функция Грина
t
x
e
t
txG
36
)(
2
6
1
),,(
ξ
π
ξ
−
−
= .
Тогда
ξ
π
ξ
ξ
dee
t
txu
t
x
2
2
36
)(
6
1
),(
−
∞+
∞−
−
−
⋅=
.
Проведем вычисление полученного интеграла. С этой целью,
выполним предварительно преобразование показателя в подынтегральном
выражении. Имеем
=
−+
+=+
+−
=+
−
t
xt
t
x
t
xx
t
x
36
2)361(
3636
2
36
)(
22
2
22
2
2
ξξ
ξ
ξξ
ξ
ξ
t
x
t
x
t
t
t
t
x
t
x
t
t
x
36136136
361
36
361361
)361(
36
2
2
2
2
2
+
+
+
−
+
=
+
−
+
−+
+
ξ
ξ
.
Таким образом,
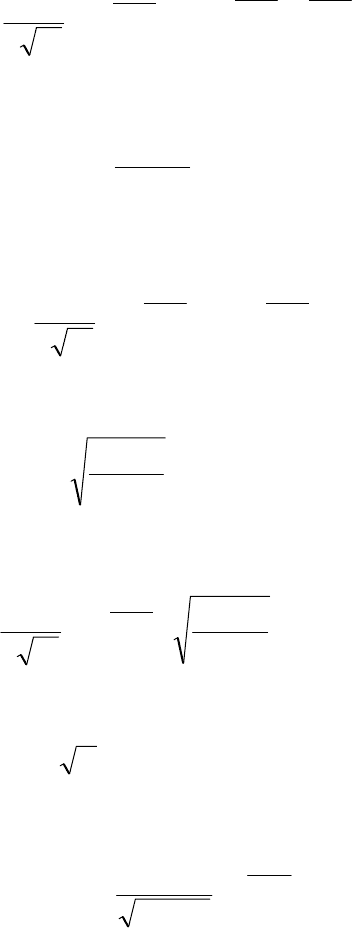
105
∞+
∞−
+
−
+
−
+
−
⋅⋅=
ξ
π
ξ
dee
t
txu
t
x
t
t
t
x
2
2
36136
361
361
6
1
),(.
Выполним теперь в интеграле замену
1
361
ξξ
=
+
−
t
x
.
Тогда, при ),( +∞−∞∈
ξ
величина ),(
1
+∞−∞∈
ξ
и
∞+
∞−
+
−
+
−
⋅⋅=
1
36
361
361
2
1
2
6
1
),(
ξ
π
ξ
dee
t
txu
t
t
t
x
.
Сделаем следующую замену
21
36
361
ξξ
=
+
t
t
;
где также ),(
2
+∞−∞∈
ξ
.Тогда
∞+
∞−
−
+
−
⋅
+
⋅⋅=
2
361
2
2
2
361
36
6
1
),(
ξ
π
ξ
de
t
t
e
t
txu
t
x
.
Учтем, что полученный несобственный интеграл есть
интеграл
Пуассона
и его значение равно
π
. Тогда, проводя очевидные упрощения,
окончательно получим
t
x
e
t
txu
361
2
361
1
),(
+
−
+
= .
Это и есть решение данной задачи. Заметим, что при наличии
малейших сомнений, в этом можно убедиться непосредственной
подстановкой.

106
Лекция 9. Разностные схемы решения простейших краевых задач
9.1. Вступительные замечания
Ниже рассматриваются методы решения краевых задач для
простейших уравнений параболического, эллиптического и
гиперболического типов вида
),(
),(
),(
txfuu
yxfuu
txfuu
xxtt
yyxx
xxt
=−
=+
=−
. (1)
Предполагается, что область
D изменения независимых переменных
является прямоугольной. Т.е.
{}
TtlxlxD ≤≤≤≤= 0 ,0:),(
для уравнений
параболического и гиперболического типов или
{}
mylxyxD ≤≤≤≤= 0,0:),(, - для эллиптического.
Обозначим через ][
u
L
левые части уравнений (1), выражение ][u
L
в
дальнейшем будем называть
дифференциальным оператором. В этом
случае уравнения (1) можно представить в виде
f
u
L
=][ . (2)
Разобьём область
D
прямыми параллельными осям координат на равные
части. Вершины этих частей будем называть узловыми точками (Рисунок 1),
а выполненное разбиение будем называть сеткой. Обозначим через
h
величину, характеризующую размер ячейки сетки (например,
h , -
наибольшая из сторон или диагональ прямоугольника). Заметим, что при
0→
h каждый из прямоугольников стягивается в точку. Обозначим через
h
u
набор значений искомой функции ),(
t
x
u или ),( y
x
u в узловых точках. Тогда
Задача численного решения краевой задачи заключается в нахождении
массива
)(h
u приближённых значений
h
u .
При разностном подходе эта задача решается следующим образом.
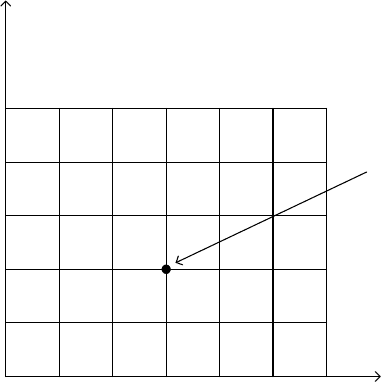
107
узловая точка (i,j)
t
T
j
0
i
l x
Рисунок 1. Построение сетки
На базе уравнения (2) формируется так называемый,
разностный
оператор
h
L . Он строится путём замены производных на разностные
отношения и выражается через значения искомой функции в узловых точках.
И, далее, вместо уравнения (2) рассматривается уравнение, или точнее,
система конечных соотношений
[
]
h
h
h
fuL =
)(
, (3)
где
h
f - набор значений функции
f
в узловых точках, для определения
набора
)( h
u . Система (3) и представляет, по существу, разностную схему. А
особенности сформулированного таким образом разностного оператора
решения краевой задачи
h
L определяют особенности вычислительного
процесса (3).
9.2. Показатели качества разностных схем
Принято качество составленной разностной схемы описывать
определёнными показателями. К их числу относятся
сходимость
вычислительного процесса, порядок аппроксимации
и устойчивость.
Опишем каждый из них.

108
Рассмотрим наборы
h
u и
)(h
u . Если при 0→h норма разности
0
)(
→−
h
h
uu , то вычислительная схема (3) называется сходящейся. Если
имеет место оценка
sh
h
hAuu ⋅≤−
)(
,
где 0>
A
, 0>
s
, то число
s
называется порядком сходимости.
Далее, пусть набор
)(h
u
представляет собой точное решение системы
уравнений (3). Очевидно, что набор
h
u , вообще говоря, этим соотношениям
не удовлетворяет. Предположим, что это различие характеризуется набором
h
f
δ
, а именно,
hhhh
ffuL
δ
+=][ .
Принято считать, что набор
h
f
δ
описывает качество аппроксимации
дифференциального оператора разностным. Предположим, что имеет место
оценка
p
h
hBf ⋅≤
δ
,
где 0>
B
, 0>
p
. Тогда число
p
называется порядком аппроксимации.
Рассмотрим понятие устойчивости. Этот показатель характеризует
чувствительность разностной схемы к тем погрешностям, которые неизбежно
допускаются в процессе вычислений. В частности, к ним относятся и
погрешности округлений. Если допускаемые неточности мало сказываются
на результатах последующих вычислений, то схема называется
устойчивой.
Эти неточности можно представить в виде возмущений правых частей
уравнений. Тогда понятие устойчивости можно трактовать так: малым
изменениям правых частей уравнений соответствуют и малые изменения в
решении. Математически это описывается следующим образом.
Вычислительная схема (3)
устойчива, если существуют
0
h
, 0>
δ
такие, что для
0
hh <∀ и
f
такого, что
δ
<f выполняется fCu
h
<
)(
.
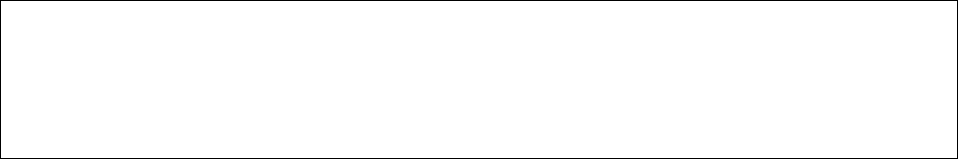
109
Оказывается, что между рассмотренными показателями существует
определённая связь. Она устанавливается следующей
теоремой.
Теорема 1. Пусть вычислительная схема устойчива и имеет порядок
аппроксимации 0>
p
. Тогда она является сходящейся и имеет порядок
сходимости
p
s
= .
Отсюда вытекает следующий порядок построения и исследования
разностных схем:
1.
проводится нахождение разностного оператора
h
L ;
2.
определяется порядок аппроксимации
p
разностной схемы (3);
3.
разностная схема исследуется на устойчивость.
Если результат выполнения последнего этапа оказывается
положительным, то разностная схема, согласно указанной теореме, является
и сходящейся.
9.3. Разностные схемы задач параболического типа
Рассмотрим, для определённости, первую краевую задачу
0 ,0 ),,( ><<=− tlxtxfuu
xxt
(4)
)()0,(
x
x
u
ϕ
= (5)
=
=
)(),(
)(),0(
2
1
ttlu
ttu
μ
μ
(6)
Разделим область ]},0;,0[),{(
T
l
y
x
D ∈= на прямоугольные части, шаг
по переменной
x
обозначим через h , шаг по переменной
t
, - через
τ
.
Выполним нумерацию узловых точек, обозначив через );(
j
i точку ),(
ji
tx ,
где
ihx
i
+= 0
,
τ
jt
j
+= 0. И для приближённого описания оператора ][u
L
в
точке ),(
j
i выберем определённую их совокупность. Этот набор называется
шаблоном. Употребительны следующие шаблоны:
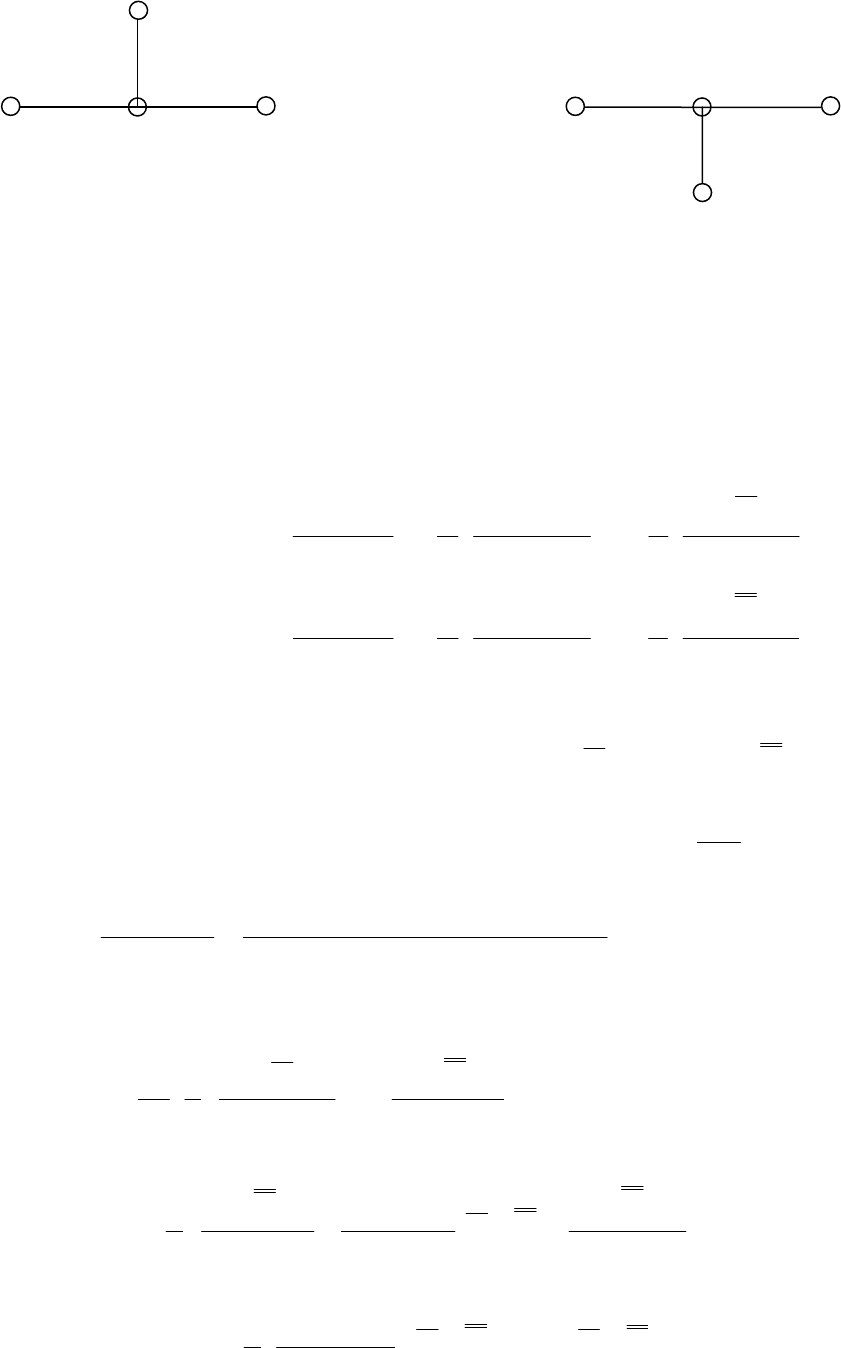
110
а) явный шаблон б) неявный шаблон
Первый из них, - шаблон а), называется
явным, второй, - шаблон б), -
неявным.
Построим выражения, аппроксимирующие в точке ),(
j
i производные,
входящие в уравнение (4). Используем для этих целей формулу Тейлора.
Имеем
3
3
3
2
2
2
1
),(
!3
1
),(
!2
1
),(
),(),(
h
x
txu
h
x
txu
h
x
txu
txutxu
jiji
ii
iiii
∂
∂
⋅+
∂
∂
⋅+
∂
∂
+=
+
3
3
3
2
2
2
1
),(
!3
1
),(
!2
1
),(
),(),(
h
x
txu
h
x
txu
h
x
txu
txutxu
jiji
ii
iiii
∂
∂
⋅−
∂
∂
⋅+
∂
∂
−=
−
Последние слагаемые в обоих выражениях представляют собой
остаточные члены в форме Лагранжа, где
),(
1+
∈
iii
xxx , ),(
1 iii
xxx
−
∈ .
Складывая теперь эти выражения и разрешая относительно
2
2
x
u
∂
∂
, получим
)(0
),(),(2),(
),(
2
2
11
2
2
h
h
txutxutxu
x
txu
jijiji
ii
+
+−
=
∂
∂
−+
, (7)
где
=
=
∂
∂
−
∂
∂
⋅=
Тейлора формуле
по слагаемые
первые Разлагая
),(),(
6
11
)(0
3
3
3
3
3
3
2
2
h
x
txu
h
x
bxu
h
h
iiii
()
=
∂
∂
−−
∂
∂
+
∂
∂
= h
x
txu
xx
x
txu
x
txu
h
i
ji
ii
iiii
),(
),
~
(),(
6
3
4
4
3
3
()
ii
ji
xx
x
txu
h
−⋅
∂
∂
⋅=
4
4
),
~
(
6
,
(
)
iii
xxx −∈
~
,
(i-1,j)
(
i
,j)
(
i+1
,j)
(
i
,j
+1
)
(
i
,j)
(
i
,j
+1
)
(i-1,j)
(
i+1
,j)
