Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.


11
Случай 1. 0=
x
. Тогда 0=y ,
3
λ
±=z , где 0≥λ .
Таким образом, множество решений
)
3
,0,0(),,(
λ
±=zyx
представляет собой множество точек, расположенных на оси OZ.
Случай 2.
x
z = . Тогда третье уравнение принимает вид
3
0
λ
=
и имеет смысл лишь при 0=λ .
Таким образом, множество решений ),,(),,(
x
x
x
zy
x
= , где
R
x
∈ и в
геометрическом плане представляет собой прямую, проходящую через
начало координат с направляющим вектором
)1,1,1(=
s
.
Заметим, что в этих точках
0=ugrad
, т.е. вырождается в точку, а
понятие параллельности точки и прямой не определено, поэтому
Ответ: (0, 0, z).
1.2. Векторное поле, дивергенция, ротор
Векторное поле. Если в каждой точке области D задан вектор а , то
говорят, что в области D задано
векторное поле.
Примером векторного поля является поле тяготения. Предположим, что
в начало координат помещена точечная масса
0
m . Тогда, на другую
точечную массу m , расположенную в точке ),,( zy
x
M
, со стороны массы
0
m ,
согласно закона всемирного тяготения, действует сила
2
0
r
mm
F γ=
, где
222
zyxr ++= . Или, с учетом направления,
−⋅⋅=
r
r
r
mm
F
2
0
γ
, т.е.
r
r
mm
F
3
0
⋅−=
γ
(Рисунок 2).

12
x
m
0
z
r
F
_
M(x,y,z)
m
y
Рисунок 2. Поле тяготения
Примерами векторных полей являются электростатическое поле,
распределение скорости в движущейся жидкости, газе и т.д.
Математически векторное поле описывается вектор-функцией
),,,( tzyxAA = . Если
A
не зависит от t, т.е. 0=
∂
∂
t
A
, то поле называется
стационарным, в противном случае, - нестационарным. Если существует
функция ),,( zy
x
u такая, что ugradA = , то поле
A
называется
потенциальным, а функция ),,( zy
x
u , - его скалярным потенциалом. Так,
например, потенциал поля тяготения
F равен
r
mm
u
0
γ
= .
Дивергенция. Рассмотрим векторное поле ),,(
321
ААAA = .
Дивергенцией поля
A
, обозначается div
A
, называется выражение
div
A
=
z
A
y
A
x
A
∂
∂
+
∂
∂
+
∂
∂
3
21
. (4)
Физический смысл. Пусть S – некоторая замкнутая поверхность,
ограничивающая объем
V (Рисунок 3), )cos,cos,(cos
γ
μ
λn , - вектор
внешней нормали.
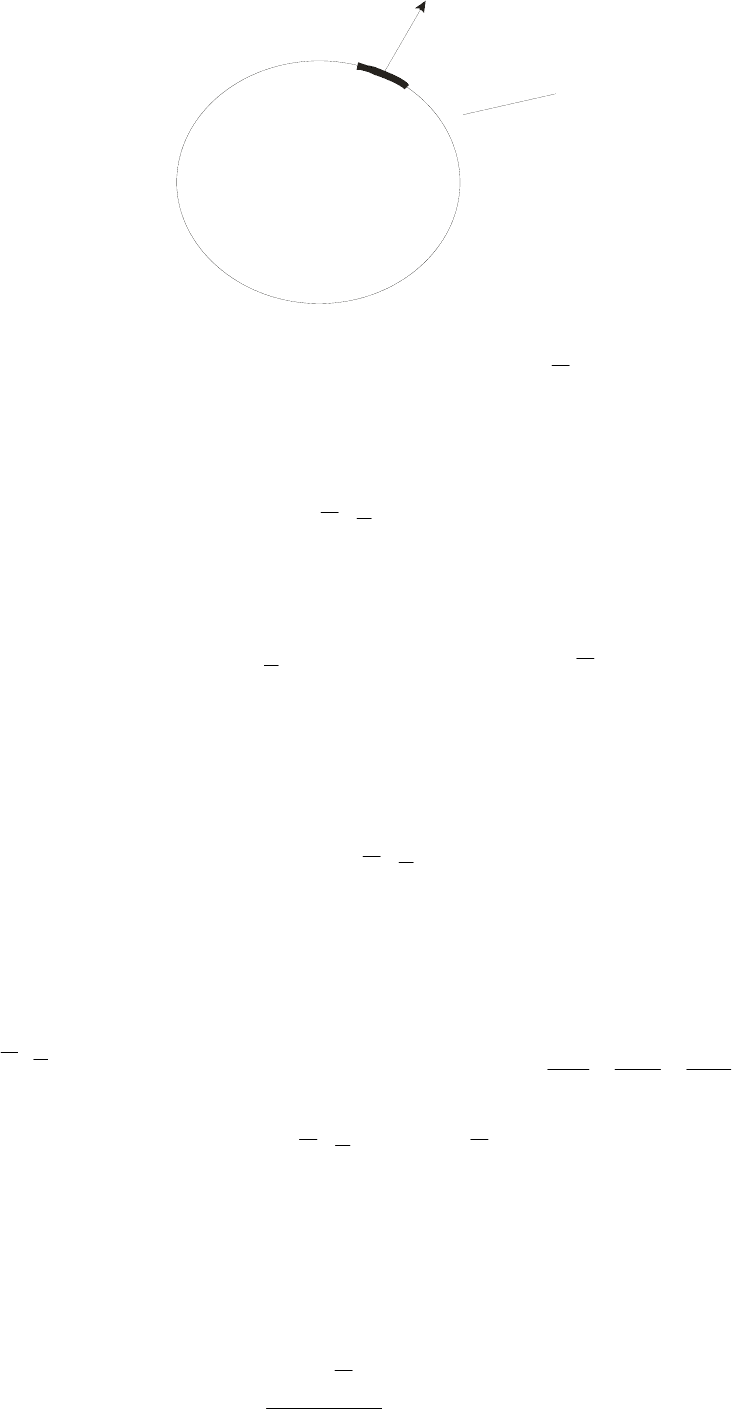
13
ds
V
n
_
S
Рисунок 3. Иллюстрация к div
A
Тогда
dsn
A
⋅ (5)
представляет собой поток векторного поля через участок поверхности
площади
ds в направлении n . Так, например, если
A
,- поле скоростей в
объеме жидкости, то (5) описывает количество жидкости, проходящей через
площадь
ds за единицу времени. Тогда
⋅
S
dsnA
,
представляет собой поток векторного поля через поверхность
S. Используя,
далее, к последнему выражению теорему Остроградского – Гаусса, имеем
∂
∂
+
∂
∂
+
∂
∂
=γ+μ+λ=⋅
S
V
S
dv
z
A
y
A
x
A
dsAAAdsnA )()coscoscos(
3
21
321
,
т.е.
=⋅
V
dvAdivdsnA
S
.
Если теперь рассмотреть отношение
V
dvAdiv

14
и перейти в нем к пределу при 0→
V
, т.е. стягивая объем в точку, получаем
)(lim
0
n
V
V
MAdiv
V
dvAdiv
=
→
.
На основании этого div
A
можно трактовать как плотность
источников
векторного поля.
Ротор. Ротором векторного поля ),,(
321
AAAА = , обозначается Arot ,
называется следующий вектор
k
y
A
x
A
j
z
A
x
A
i
z
A
y
A
Arot
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
=
121
3
2
3
.
Его физический смысл состоит в следующем.
Рассмотрим в векторном поле
A
замкнутый контур l, ограничивающий
поверхность
S. Тогда криволинейный интеграл
l
dlA
называется
циркуляцией поля
A
вдоль контура l. Обозначим через
)cos,cos,(cos
γ
μ
λ=n нормальный вектор к поверхности S, причем
предположим выполненным согласование направления
n и обхода контура
l. Тогда, согласно теореме Стокса,
⋅=
S
l
dsnArotdlA .
Т.е.
Циркуляция поля вдоль контура
l равна потоку ротора этого поля через
поверхность S.
15
По аналогии со скалярным потенциалом в теории поля вводится и
понятие векторного потенциала. А именно, вектор
B
называется векторным
потенциалом
поля
A
, если
A
В
rot =
Замечание. В теории поля Arot называется еще вращением или
вихрем поля А. Если 0=Arot , то поле
A
называют безвихревым.
1.3. Оператор Гамильтона
Оператором Гамильтона, обозначается ∇ , называется следующее
символическое выражение
k
z
j
y
i
x
∂
∂
+
∂
∂
+
∂
∂
=∇
.
Его действие в скалярных и векторных полях определяют так:
k
z
u
j
y
u
i
x
u
u
∂
∂
+
∂
∂
+
∂
∂
=∇
,
k
z
uj
y
ui
x
uu
∂
∂
+
∂
∂
+
∂
∂
=∇
,
,
3
21
z
A
y
A
x
A
A
∂
∂
+
∂
∂
+
∂
∂
=∇
,
121
3
2
3
321
k
y
A
x
A
j
z
A
x
A
i
z
A
y
A
AAA
zyx
kji
A
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
=
∂
∂
∂
∂
∂
∂
=×∇

16
z
A
y
A
x
AA
∂
∂
+
∂
∂
+
∂
∂
=
∇ 321
,
.
213232321
k
x
A
y
Aj
y
A
z
Ai
y
A
z
A
zyx
AAA
kji
A
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
=
∂
∂
∂
∂
∂
∂
=∇×
Отсюда следует, что
uugrad ∇=
AAdiv ∇=
AArot ×∇= .
1.4 . Повторные дифференциальные операции
Если к выражениям
u∇ , Adiv , Arot снова применить рассмотренные
выше операции, то получим
повторные дифференциальные операции.
Их всего пять:
udiv∇ , urot∇ ,
A
di
v
, Arotdiv , Arotrot . Рассмотрим их
более подробно.
1.
udiv∇ . Очевидно, что
2
2
2
2
2
2
z
u
y
u
x
u
k
z
u
j
y
u
i
x
u
divudiv
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
=∇
.
Т.е.
2
2
2
2
2
2
z
u
y
u
x
u
udiv
∂
∂
+
∂
∂
+
∂
∂
=∇
(6)
Введем дополнительное символическое выражение
2
2
2
2
2
2
zyx ∂
∂
+
∂
∂
+
∂
∂
=Δ
,
называемое
оператором Лапласа.

17
Тогда
uudi
v
Δ=∇ , (6
1
)
а сам оператор Δ , учитывая принятые выше договоренности, можно
представить в виде
2
∇=∇⋅∇=Δ
Тогда
uudi
v
2
∇=∇ (6
2
)
Таким образом, выражения (5), (5
1
), (5
2
) представляют собой
эквивалентные представления одной и той же операции.
2.
uro
t
∇ . Имеем
,0000
222222
=⋅+⋅+⋅=
=
∂∂
∂
−
∂∂
∂
+
∂∂
∂
−
∂∂
∂
−
∂∂
∂
−
∂∂
∂
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=∇
kji
k
yx
u
yx
u
j
zx
u
zx
u
i
yx
u
yx
u
z
y
y
y
x
y
zyx
kji
urot
т.к. нулевой вектор отождествляется с точкой.
К этому результату можно было бы прийти и так. Учитывая введенные
выше соглашения о замене произведения дифференцированием (т.е.
,
2
yxyx ∂∂
∂
→
∂
∂
⋅
∂
∂
например), имеем
00)( =⋅=∇×∇=∇×∇=∇ uuuurot
3.
Adiv∇ .

18
k
z
A
zy
A
zx
A
j
xz
A
y
A
yx
A
i
xz
A
yx
A
x
A
z
A
y
A
x
A
Adiv
∂
∂
+
∂∂
∂
+
∂∂
∂
+
∂∂
∂
+
∂
∂
+
∂∂
∂
+
+
∂∂
∂
+
∂∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
∇=∇
2
3
2
2
2
1
2
3
2
2
2
2
1
2
3
2
2
2
2
1
2
3
21
4.
Arotdiv
.0
)(
1
2
2
2
1
2
3
2
2
2
3
2
121
3
2
3
321
=
∂∂
∂
−
∂∂
∂
+
∂∂
∂
+
∂∂
∂
−
∂∂
∂
−
∂∂
∂
=
=
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
⋅∇=
=
∂
∂
∂
∂
∂
∂
⋅∇=×∇⋅∇=
zy
A
zx
A
zy
A
yx
A
xz
A
yx
A
k
y
A
x
A
j
z
A
y
A
i
z
A
y
A
AAA
zyx
kji
AArotdiv
Таким образом
.0=Arotdiv
5.
A
rotro
t
.
)(
2
2
2
3
2
1
2
2
3
2
2
1
2
3
2
2
1
2
2
2
2
2
1
2
3
2
2
1
2
2
2
321
k
zy
A
y
A
zx
A
x
A
j
z
A
zy
A
y
A
x
A
i
z
A
zx
A
y
A
yx
A
AAA
zyx
kji
rotArotrot
∂∂
∂
+
∂
∂
−
∂∂
∂
+
∂
∂
−+
∂
∂
+
∂∂
∂
−
∂
∂
−
∂
∂
−
−
∂
∂
−
∂∂
∂
+
∂
∂
−
∂∂
∂
=
∂
∂
∂
∂
∂
∂
=

19
Сравнивая, далее, полученное соотношение с
A
div∇ получаем
AAdivArotrot Δ−∇=
Задание. Найти uΔ , если
222
,
1
zyxr
r
u ++== .
Решение. 1) Найдем
x
u
∂
∂
.
Используя правило дифференцирования сложной функции, имеем
,
111
2
r
x
r
x
r
rrrxx
u
⋅
−=
∂
∂
⋅
∂
∂
=
∂
∂
=
∂
∂
т.е.
3
r
x
x
u
−=
∂
∂
Тогда
,
3
6
23
32
2
r
r
x
rxr
r
x
x
x
u
⋅⋅−
−=
−
∂
∂
=
∂
∂
т.е.
4
223
2
2
r
xzy
x
u −+
−=
∂
∂
.
2) Функция
r, и следовательно, функция u являются симметричны
относительно переменных
x, y, z, т.е. r(x, y, z) = r(y, x, z) = и т.д. На
результатах дифференцирования это отражается в том, что производные по
другим переменным определяются по аналогии. Т.е.
4
222
2
2
2
r
yzx
y
u −+
−=
∂
∂
.
2
4
222
2
2
r
zyx
z
u −+
−=
∂
∂

20
3) Складывая, далее, полученные соотношения, имеем
0
222
4
222
4
222
4
222
=
−+
−
−+
−
−+
−=Δ
r
zyx
r
yzx
r
xzy
u
.
т.е. 0
=Δu .
Замечание. Уравнение
0
=Δu ,
называется
уравнением Лапласа, а его решения, - гармоническими
функциями
. Т.о. функция
r
u
1
= , в трехмерной области, не содержащей
начало координат, является гармонической.
Лекция 2. Уравнения в частных производных, классификация,
приведение к каноническому виду
2.1. Вступительные замечания
Большое число физических задач приводят к дифференциальным
уравнениям с частными производными второго порядка относительно
искомой функции – измеряемой физической величины, зависящей, вообще
говоря, от времени и положения в пространстве. Такие уравнения можно
записать в виде соотношений между независимыми переменными
х
1
…
n
x ,
искомой функцией
u и ее частными производным первого и второго
порядков
nnjinn
xxxxxxxxxx
u,...,u,...u,...,u;u,...,u
1211
(1)
0
1121
21
=)u,u,...,u;u,...,u,u,u;x,...,x,x(F
nnjin
xxxxxxxxxn
