Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.


121
[]
)2()1()()1()()1(
5199
24
−−++
+−++=
kkkkkk
FFFFuu
τ
.
Это уже неявная схема и для получения значений функции u на очередном
временном слое требует выполнения ряда итераций.
10.3. Метод конечного элемента
Первоначально разработанный для решения задач теории упругости и
расчёта конструкций позднее этот метод стал использоваться и для решения
краевых задач математической физики. Концептуально он заключается в
следующем.
На первом этапе исходную краевую задачу заменяют эквивалентной
задачей обычно налагающей более слабые требования на гладкость искомой
функции. В частности, в качестве такой
может выступать задача о
нахождении экстремума некоторого функционала, оптимизирующая функция
которого является и решением рассматриваемой краевой задачи. Далее,
решение новой задачи приближённо ищется в виде линейной комбинации
некоторых базисных функций (это методы Галёркина, Ритца, коллокаций) с
неизвестными коэффициентами. Одной из характерных особенностей метода
конечных элементов является выбор базисных функций, производится это
следующим образом. Область изменения геометрических переменных
разбивается на конечные части в виде выпуклых многоугольников, или
многогранников в трёхмерном случае, на плоскости это, обычно,
треугольники или прямоугольники, а их вершины принимаются в качестве
узловых точек. В качестве базисной функции принимается функция,
представляющая собой линейную форму на конкретном конечном участке и
равную 0
вне его. Таким образом, формируется набор функций число
которых равно числу конечных элементов. Обратим внимание, что
расположение узловых точек может выбираться произвольно с учётом

122
априорных представлений о поведении искомой функции, т.е. их
равномерное распределение совсем не обязательно.
Рассмотрим для иллюстрации двумерную краевую задачу
параболического типа
fuu
t
+Δ= , (8)
где ),,(
t
y
x
uu = , Dy
x
∈),(,
0
tt >
2
2
2
2
yx ∂
∂
+
∂
∂
=Δ
,
),,(
t
y
x
f
f
=
и
∂∈=
=
Dyxtyxu
yxutyxu
),( для ,0),,(
),(),,(
00
. (9)
Показано, что эта задача эквивалентна, так называемой, слабой форме
задачи, имеющей вид
()
),(),(, vfvuavu
t
=+ , (10)
с начальным условием
()
vuvu
tt
,),(
0
0
=
=
, (11)
для
H
v
∈∀ , где выражения
∂
∂
=
∂
∂
D
vdxdy
t
u
v
t
u
,,
=
D
dxdyyxvtyxfvf ),(),,(),(
представляют собой скалярные произведения в функциональном
пространстве
H
, - множестве функций интегрируемых со своим квадратом в
области
D , а
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
D
dxdy
y
v
y
u
x
v
x
u
vua ),(

123
представляет аналог оператора Лапласа. Оказывается, что функция ),,(
t
y
x
u ,
удовлетворяющая задаче (10), (11) является и решением задачи (8), (9). В
этом смысле задачи (8), (9) и (10), (11) эквивалентны.
Решение задачи (10), (11), т.е. функция ),,,(
t
z
y
x
u , ищется методом
Галёркина. Предполагается, что
=
=
N
i
ii
yxtu
1
),()(
ϕα
, (12)
где
i
ϕ
- базисные функции. Подставляя (12) в (10) получаем систему
линейных дифференциальных уравнений для определения )(t
i
α
() ()
()
=
==
⋅+
N
j
iijiij
i
Nifa
dt
d
1
,1 ,,,,
ϕϕϕαϕϕ
α
, (13)
с начальными условиями
jki
ct =)(
α
, (14)
где
j
c - коэффициенты разложения функции ),,(
t
y
x
u на рассматриваемом
временном слое по базисным функциям и определяются из соотношений
()
()
=
==
N
j
ikijj
Nityxuc
1
,1 ,),,,(,
ϕϕϕ
.
На начальном временном слое
0
tt = значения ),(),,(
00
yxutyxu = .
Система (13), (14) используется для нахождения функций )(t
i
α
и,
совместно с (12), последующего продвижения на величину
t
Δ по переменной
t
, т.е. для определения ),,(
t
y
x
u на следующем временном слое. После этого
производится определение значений функции ),,(
t
y
x
u в узловых точках
),(
kk
yx , построения по наборам значениям ),,(
kkk
yxu очередной системы
базисных функций и последующего решения системы (13), (14).
Формирование базисных функций на каждом временном слое
производится так. Пусть исходная геометрическая область разделена на
треугольные конечные элементы и пусть
321
AAAΔ с вершинами ),(
111
yxA ,
),(
222
yxA , ),(
333
yxA один из них, условно i -ый элемент (рисунок 1).
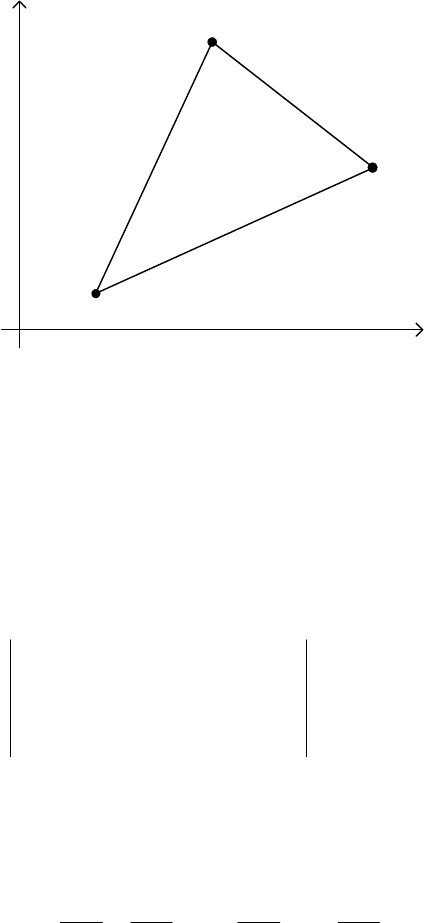
124
y
x
A
1
A
2
A
3
Рисунок 1. Треугольный конечный элемент
Пусть
321
,, uuu значения функции ),,,(
t
z
y
x
u в этих точках
соответственно. Тогда линейная интерполяция геометрически представляет
собой плоскость, точнее, часть плоскости, проходящую через точки
),,(
111
uyx , ),,(
222
uyx , ),,(
333
uyx . Её уравнение имеет вид
0
131313
121212
111
=
−−−
−−−
−−−
uuyyxx
uuyyxx
uuyyxx
.
Раскрывая теперь определитель по третьему столбцу и обозначая u через
i
ϕ
,
получим
3
3
33
3
3
23
1
3
33
3
23
1 u
A
A
u
A
A
u
A
A
A
A
i
−−
++=
ϕ
,
где
ij
A - алгебраические дополнения к элементам третьего столбца.
Более подробно о методе, вопросах его сходимости и применения к
другим типам краевых задач см. Э. Митчелл, Р. Уэйт. Метод конечных
элементов для уравнений с частными производными. М.: Мир, 1981. – 216 с.
125
Рекомендуемая литература
1.
Арсенин В.Я. Методы математической функции и
специальные функции. - М.: Наука, 1974.
2.
Г. Корн, Т. Корн. Справочник по математике для научных
работников и инженеров. - М.: Наука, 1970.
3.
Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в
частных производных математической физики. - М.: Высшая
школа, 1970.
4.
Крылов В.И., Бобков В.В., Монастырный П.И.
Вычислительные методы. Т.2. - М.: Наука, 1977.
5.
Митчелл Э., Уэйт Р. Метод конечных элементов для
уравнений с частными производными. - М.: Мир, 1981.
6.
Чудесенко В.Ф. Сборник заданий по специальным курсам
высшей математики (типовые расчеты). — М: Высшая школа,
1983 (1994).
126
Предметный указатель
Гамма-функция 88
Градиент скалярного поля 9
Дивергенция векторного поля 12
Задача Коши 56,63
— краевая 55
— Штурма-Лиувилля 69
Значения собственные 69
Жидкость идеальная 51
Интеграл Пуассона 105
Мембрана 45
Оператор Гамильтона 15
— дифференциальный 106
— Лапласа 16
— разностный 107
Операции дифференциальные повторные 16
Поле векторное 11
— — стационарное 12
— — нестационарное 12
— скалярное 6
— — стационарное 6
— — нестационарное 6
Потенциал векторный 15
— скалярный 12
Преобразование Фурье 101
— — прямое 102
— — обратное 102
Производная по
направлению 6
Процесс вычислительный
— —, сходимости 107, 108
— —, порядок аппроксимации 107, 108
— —, устойчивости 107, 108
Ротор векторного поля 14
Струна 40
Схема разностная
— —, явная 111
— —, неявная 111
Уравнение Бесселя 87, 88
— волновое 44
— гидродинамики и акустики 53
— гиперболического типа 24, 25
— диффузии 50
— каноническое 21, 25
— квазилинейное 21
127
— линейное 21
— — неоднородное 21
— — однородное 21
— параболического типа 24, 31
— состояния 53
— теплопроводности 50
— характеристик 28
— эллиптического типа 24, 30
— Эйлера 95
Условия начальные 55
— граничные 55
Функция Грина 98
— Дирака,
δ
-функция 62, 97
— Неймана 88
— обобщённая 62
Функции собственные 69
— цилиндрические 88
Циркуляция поля 14
Шаблон неявный 110
— явный 110
