Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.

111
где hxx
ii
2≤− .
Аналогичным образом, выполним разложение по переменой
t
2
2
2
1
),(
!2
1
),(
),(),(
ττ
t
txu
t
txu
txutxu
jiji
jiji
∂
∂
⋅+
∂
∂
+=
+
и
2
2
2
1
),(
!2
1
),(
),(),(
ττ
t
txu
t
txu
txutxu
jiji
jiji
∂
∂
+
∂
∂
−=
−
.
Тогда из первого из этих соотношений
τ
τ
2
2
1
),(
!2
1
),(),(),(
t
txutxutxu
t
txu
jijijiji
∂
∂
⋅−
−
=
∂
∂
+
(8)
из второго, -
2
2
2
1
),(
!2
1
),(),(),(
τ
τ
t
txutxutxu
t
txu
jijijiji
∂
∂
⋅+
−
=
∂
∂
−
(9)
Используя (7), (8) для шаблона а), получим
),()(0)(0
),(),(2),(),(),(
2
2
111
ji
jijijijiji
txfh
h
txutxutxutxutxu
=++
+−
−
−
−++
τ
τ
Отбрасывая в последнем соотношении величины )(0)(0
2
h+
τ
получаем
явную разностную схему
j
i
j
i
j
i
j
i
j
i
j
i
f
h
uuuuu
=
+−
−
−
−+
+
2
11
1
2
τ
, (10)
где нижний индекс указывает номер узловой точки по переменной
x
,
верхний, - по переменной
t
. Обратим внимание, что соотношение (10)
разрешимо относительно
1+j
i
u , т.е. значения функции на следующем
временном слое, что существенно облегчает решение.
Действуя аналогичным образом, для шаблона б) получим
неявную
разностную схему.
j
i
j
i
j
i
j
i
j
i
j
i
f
h
uuuuu
=
+−
−
−
−+
−
2
11
1
2
τ
. (11)

112
Её особенностью является то, что она неразрешима относительно
значений
j
i
u
на следующем временном слое. Однако, в целом,
соответствующая система уравнений трёхдиагональна и для её решения
используются специальные методы, одним из наиболее употребительных из
которых является
метод прогонки.
Если теперь к (10) или (11) добавить начальные и граничные условия
ii
u
ϕ
=
0
j
j
u
10
μ
= ,
j
j
N
u
2
μ
= ,
получим замкнутую задачу для нахождения значений
1+j
i
u на )1( +
j
-ом
временном слое, в случае схемы (10), и значений
j
i
u на
j
-ом временном
слое, в случае схемы (11).
Устойчивость разностных схем. Обозначим отношение
r
h =
2
/
τ
.
Будем предполагать, что оно остаётся постоянным при проведении
вычислений. Это означает, что изменение шага по одной из переменных
влечёт соответствующее изменение шага и по другой.
При этих условиях показано, что явная схема оказывается устойчивой,
если
2
1
≤r
, неявная, - при 0>
r
, что естественно выполняется автоматически.
Таким образом, неявная схема является глобально устойчивой. Кроме этого,
следует отметить, что обеспечение устойчивости в случае явной разностной
схемы требует большего дробления шага, и, влечёт к большим объёмам
вычислений по сравнению с неявной.
Порядок аппроксимации. При замене дифференциального оператора
разностным величина производимой погрешности обуславливается
величиной )(0)(0
2
h+
τ
. Показано, что при значениях
r
h =
2
/
τ
,
обеспечивающих устойчивость разностных схем, порядок аппроксимации
явной разностной схемы 2=
p
, неявной 1=
p
.
113
Сходимость. В соответствии с теоремой 1 (п.2) можно утверждать, что
при выполнении указанных выше требований относительно устойчивости,
явная разностная схема имеет порядок сходимости 2=
s
, неявная, - 1=
s
.
9.4. Разностные схемы задач эллиптического типа
В качестве примера, рассмотрим первую краевую задачу для уравнения
Пуассона в прямоугольнике
),( yxfuu
yyxx
=+ , a
x
<<0, by <<0
)(),0(
1
yyu
ϕ
= , )(),(
2
yyau
ϕ
=
)()0,(
1
xxu
ψ
= , )(),(
2
xbxu
ψ
=
Разобьём область ]},0[],;0[:),{( bya
x
y
x
D ∈∈= на равные
прямоугольные части со сторонами h и
l
по переменным
x
и y ,
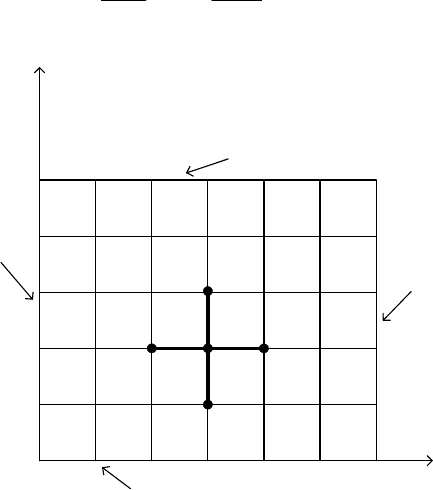
соответственно, и рассмотрим трёхслойный пятиточечный шаблон (Рисунок
2), где ihx
i
= , jly
j
= для Ni ,0= , Mj ,0= .
y
b
j
0
i
a x
(i+1,j)
(i,j-1)
(i-1,j)
(i,j+1)
)(
2
x
ψ
)(
2
y
ϕ
)(
1
y
ϕ
)(
1
x
ψ
Рисунок 2. Шаблон, используемый для аппроксимации
114
Используем изложенный выше (см. п. 3) подход для аппроксимации
входящих в уравнение производных. В результате получим следующую
разностную схему для внутренних точек ),(
j
i области D
ji
jijijijijiji
f
l
uuu
h
uuu
,
2
1,,1,
2
,1,,1
22
=
+−
+
+−
−+−+
(12)
Если к (12) добавить граничные сеточные условия
jj
u
1,0
ϕ
= ,
jjN
u
2,
ϕ
= ,
ii
u
10,
ψ
= ,
iMi
u
2,
ψ
= ,
где
Ni ,0=
, Mj ,0= , получим замкнутую систему уравнений для
определения приближённых значений функции ),( y
x
u во внутренних
узловых точках.
Полученная вычислительная схема обладает следующими
особенностями:
1.
при 0
/
>=
r
h
l
схема устойчива;
2.
при const
r
= она имеет порядок аппроксимации 2=
p
;
3.
схема является сходящейся и имеет порядок сходимости 2=
s
.
Замечание. Отметим, что вид уравнения определяет и вид используемого
шаблона. Так, например, для уравнения
),(4 yxfuuu
yyxyxx
=++ ,
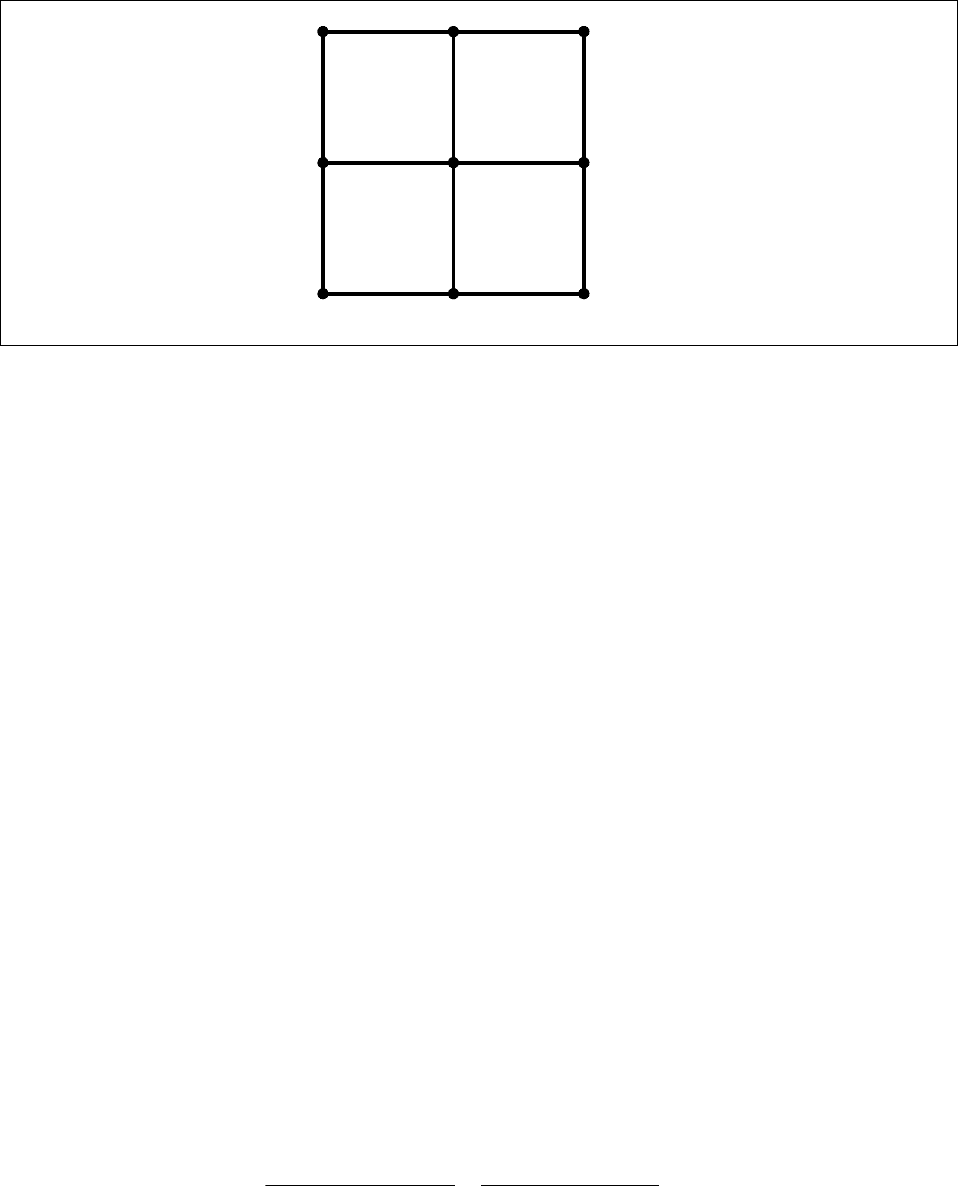
которое по-прежнему является гиперболическим, прежнего шаблона уже
недостаточно. В этом случае используется трёхслойный девятиточечный
шаблон
115
h
l
(i,j)
(i+1,j+1)
(i-1,j-1)
9.5. Разностная схема задачи гиперболического типа
Рассмотрим для определённости первую краевую задачу для
одномерного волнового уравнения
),( txfuu
xxtt
=− ,
l
x
<<0, 0>
t
=
=
)()0,(
)()0,(
2
1
xxu
xxu
t
ϕ
ϕ
,
l
x
<<0
)(),0(
2
ttu
μ
= , )(),(
2
ttlu
μ
= , 0>
t
.
Используем изложенные выше подходы к построению разностных
схем. Также будем предполагать область D прямоугольной, т.е.
l
x
≤≤0,
T
t
≤≤0. Проведём аналогичное разбиение области
D
с шагом h и
τ
по
переменным
x
и
t
, соответственно и применим трёхслойный пятиточечный
шаблон (см. п. 4).
Тогда для аппроксимации уравнения в узловой точке ),(
j
i получим
следующую разностную схему
j
i
j
i
j
i
j
i
j
i
j
i
j
i
f
h
uuuuuu
=
+−
−
+−
−+
−+
2
11
2
11
22
τ
. (13)
где также, как и ранее, нижний индекс соответствует переменной
x
верхний – переменной
t
. К этим соотношениям необходимо добавить ещё те,
которые вытекают из начальных и граничных условий, а именно, -

116
===
==
−
=
Mjuu
Ni
uu
u
j
j
Nj
j
i
ii
ii
,0 , ,
,0 , ,
210
2
01
1
0
μμ
ϕ
τ
ϕ
. (14)
Схема (13), (14) является явной, т.е. разрешимой относительно
1+j
i
u
и
имеет следующие характеристики.
Обозначим 0
/
>=
r
h
τ
. Тогда
1.
при 1<
r
схема является устойчивой,
2.
имеет порядок аппроксимации 2=
p
,
3.
является сходящейся и имеет порядок сходимости 2=
s
.
9.6. Оценка погрешности численных решений
При численных расчётах используют различные подходы для оценки
погрешности численных решений. Один из них заключается в использовании
правила Рунге. Его сущность заключается в следующем.
Оказывается, что главный член погрешности метода имеет вид
p
hyx ),(
ρ
, где
p
- порядок погрешности метода, h - параметр,
определяющий размер сетки. Тогда приближённо можно считать, что
p
h
hyxyxuyxu ),(),(),(
ρ
≈−
где ),( y
x
u , - точное значение искомой функции, ),( yxu
h
- приближённое,
полученное с шагом h . Тогда проведя расчёты с половинным шагом 2
/
h ,
получим
p
h
hyxyxuyxu )2/)(,(),(),(
2/
ρ
≈− (16)
Разрешим теперь систему соотношений (15), (16) относительно ),( y
x
ρ
.
Получим
pp
hh
hh
yxuyxu
yx
)2/(
),(),(
),(
2/
−
−
≈
ρ
Подставив теперь полученное соотношение в (16), получим

117
12
),(),(
),(),(
2/
2/
−
−
≈−
p
hh
h
yxuyxu
yxuyxu ,
представляющей собой оценку погрешности приближённого решения
),(
2/
yxu
h
. Таким образом, проводя последовательно вычисление с шагом h и
2
/
h получаем возможность контролировать погрешность вычислений в
общих узловых точках.
Другой подход заключается в следующем. Проводят вычисления с
шагом h и 2
/
h и сравнивают значения в общих узловых точках.
Совпадающие десятичные знаки считаются верными.
Лекция 10. Многомерные краевые задачи, некоторые методы их
решения
Многомерными здесь будем называть задачи, содержащие более одной
геометрической переменной. Изложим некоторые подходы к их решению,
получившие распространение в последние десятилетия.
10.1. Методы расщепления
В этих методах исходная многомерная разностная схема с помощью
специальных процедур разбивается на ряд одномерных. После этого к
последним применяют экономичные вычислительные методы, в результате
чего суммарная трудоёмкость исходной задачи существенно снижается.
Рассмотрим в качестве примера двумерное уравнение
теплопроводности
),,( tyxfuuu
yyxxt
++= .

118
Используя, как более устойчивый, неявный пятиточечный шаблон, обычным
образом (см. Лекция 9) аппроксимируем входящие в уравнение производные,
в результате чего получим соответствующую разностную схему
k
ij
ij
k
ij
k
ijji
k
ij
k
ji
k
ij
k
ij
f
h
uuu
h
uuuuu
+
+−
+
+−
=
−
−+−+
−
2
11
2
,1,1
1
22
τ
, (1)
Здесь шаг по переменным
x
, y был выбран одинаковым и равным h .
Система соотношений (1) представляет собой линейную систему уравнений
для определения приближённых значений функции ),,(
t
y
x
u на k -ом
временном слое. Её можно представить в виде
b
A
u
k
= , (2)
где
k
u
- набор длины
N
значений ),,(
t
y
x
u в узловых точках ),(
j
i ,
A
-
постоянная матрица порядка
N
N
× , b - вектор, определяемый значениями
),,(
t
y
x
u и функцией ),,(
t
y
x
f
на )1( −k -ом временном слое. В одномерных
задачах матрица
A
имеет трёхдиагональный вид и решение системы (2)
проводится методом прогонки, имеющим трудоёмкость равную )(0
N
.
Однако, в многомерных схемах, построенных на базе (1), соответствующая
система уравнений (2) трёхдиагональной уже не является. Поэтому, для её
решения необходимо использовать уже иные, менее экономичные методы, а
это отражается и на общей трудоёмкости решения. Так, например, при
использовании метода Гаусса для решения системы (2) общее число
арифметических операций составляет уже величину порядка
3
N
.
Изложим идею расщепления.
Выполним очевидное преобразование схемы (1)
k
ij
k
ij
ij
k
ij
k
jiji
k
ij
k
ji
k
ij
fu
h
uuu
h
uuu
u
ττ
+=
+−
+
+−
−
−
−+−+
1
2
11,
2
,1,1
22
(3)
и обозначим, входящие в (3), разностные операторы через
2
,1
,1
2
h
kuuu
u
ji
k
ij
k
ji
k
ijxx
−
+
+−
=Λ ,
2
11
2
h
uuu
u
k
ij
k
ij
k
ij
k
ijyy
−+
+−
=Λ ,
119
k
ij
k
ij
k
ij
fuF
τ
+=
−1
,
k
ij
k
ij
uEu = .
Тогда систему соотношений (3) можно представить в виде
()
k
ij
k
ijyyxx
FuE =⋅Λ+Λ− )(
τ
или в матричной форме
()
kk
yyxx
FuE =⋅Λ+Λ− )(
τ
, (4)
где
{
}
k
ij
k
uu = ,
{
}
k
ij
k
FF = . Здесь имеется в виду, что
{}
k
ijxx
k
xx
uu Λ=Λ
и т.д. Т.е. применение оператора
Λ к набору
k
u
эквивалентно его
применению к каждому элементу этого набора.
Рассмотрим теперь схему
kk
yyxx
FuEE =Λ−Λ− ))((
ττ
. (5)
В развернутом виде она имеет вид
()
kk
yyxxyyxx
FuE =⋅ΛΛ+Λ+Λ−
2
)(
ττ
.
Очевидно, что левые части вычислительных схем (4), (5) отличаются на
малые порядки
2
τ
. Поэтому в тех случаях, когда это несущественно, в
теории эти вопросы изучаются, наборы значений
k
u полученные при
использовании вычислительных схем (4), (5), близки. Однако схему (5)
можно разбить на две одномерные. А именно,
()
()
=Λ−
=Λ−
kk
yy
kk
xx
vuE
FvE
τ
τ
, (6)
где
k
v - вспомогательный промежуточный набор. Таким образом, решив
последовательно две одномерные трёхдиагональные схемы (6), получим
приближённое решение задачи (4) и, следовательно, задачи (3), достигнув
при этом трудоёмкости равной )(02
N
⋅ , т.е. величины )(0
N
.
Изложенный подход использовался, в частности, к решению задач
прогноза погоды в ВЦ АН СССР и описан в монографии Г.И. Марчук.

120
Численное решение задач динамики атмосферы и океана. Л.:
Гидрометеоиздат, 1974. – 304с.
10.2. Комбинированные подходы
Известны результативные попытки использования для дискретизации
по одной из переменных, например, по переменной
t
, приближённых
методов решения обыкновенных дифференциальных уравнений.
Такой подход использовался, в частности, также при моделировании
задач прогноза погоды (см., например, Mac Donald A.E., Lee I.L., Sun S. QNH:
Design and Test of a Quasinonhydrostatic Model for Mesoscale Weather
Production. – Monthly Weather – Review, Vol. 128, p. 1016-1036) и заключается
в следующем.
Пусть, имеется система уравнений параболического типа
(
)
tuuuuuzyxFu
yyxxyxt
,,,,,,,,= . (7)
Тогда дискретизация по времени с использованием метода Адамса-Башфорта
третьего порядка приводит к следующей схеме
[]
)2()1()()()1(
51623
12
−−+
+−+=
kkkkk
FFFuu
τ
.
Это явная схема, требует одного вычисления правых частей уравнений на
каждом шаге интегрирования и оказывается устойчивой при определённых
соотношениях между
τ
и h , - шагом дискретизации по геометрическим
переменным. Для вычисления наборов значений функции u на двух первых
временных шагах используется метод Адамса-Башфорта первого порядка. К
числу особенностей этой схемы можно отнести необходимость удерживать в
оперативной памяти наборы значений правых частей уравнений на трёх
временных слоях.
Наряду с приведённой схемой, для
решения задач климатологии
апробировалась также схема, основанная на методе Адамса-Мултона
третьего порядка. Применительно к системе (7) она выглядит так
