Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.

61
Задача 4. Поставить краевую задачу о поперечных колебаниях струны
с закрепленными концами, нагруженной в точке
0
x сосредоточенной массой
0
m .
Решение. Один из вариантов постановки основан на δ-функции
Дирака. Изложим минимально необходимые сведения о ней.
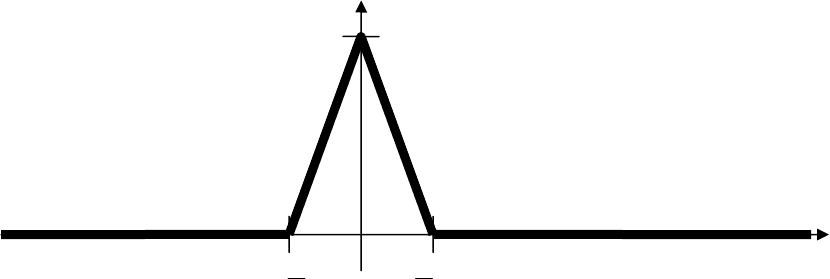
Рассмотрим последовательность
{}
)(x
n
ϕ
непрерывных функций, где
)(x
n
ϕ
представляет собой кусочно-линейную функцию и имеет следующий
вид
Очевидно, что при ∞→n последовательность
)()( xx
n
δ
ϕ
→ , где
≠
=∞+
=
0 , 0
0 ,
)(
x
x
x
δ
,
причём на любых отрезках
[]
)0;(; −∞⊂BA
или
[]
);0(; +∞⊂BA
эта сходимость
равномерная. Оказывается, что свойства функции )(
x
δ
определяются
свойствами генерирующей её последовательности )(x
n
ϕ
. В частности, можно
показать, что
+∞
∞−
=− )()()(
00
xdxxxx
ϕδϕ
для любой непрерывной функции )(
x
ϕ
, откуда
=−
B
A
xdxxxx )()()(
00
ϕδϕ
на произвольном отрезке [A;B], содержащем точку
0
x и
n
x
)(x
n
ϕ
n
1
−
n
1
62
+∞
∞−
= 1)( dxx
δ
.
Функции, определяемые подобным образом, называются
обобщёнными, а
функция )(
x
δ
, - δ-функцией Дирака.
В данной задаче плотность )(
x
ρ
струны с сосредоточенной на ней
массой можно описать с помощью δ-функции. А именно,
)()()(
000
xxmxx −+=
δ
ρ
ρ
, где )(
0
x
ρ
- линейная плотность непосредственно
струны, и краевая задача принимает вид
0 , 0 , ))()((
0000
><<=−+ tlxuTuxxmx
xxtt
δ
ρ
<<=
=
lxxxu
xxu
t
0 , )()0,(
)()0,(
ψ
ϕ
0,0),(),0( >==
t
t
l
u
t
u .
Напомним, что при малых поперечных колебаниях струны сила
натяжения
0
T постоянна.
Лекция 5. Задача Коши для одномерного волнового уравнения, решение
Даламбера
5.1. Постановка задачи
Формулируется так.
Необходимо найти решение уравнения
xxtt
uau
2
= , +∞<<∞−
x
, (1)
удовлетворяющего начальным условиям
=
=
)()0,(
)()0,(
xxu
xxu
t
ψ
ϕ
, +∞<<∞−
x
(2)

63
Такая задача называется задачей Коши. Заметим, что в данном случае
граничные условия отсутствуют. Задача может описывать, в частности,
поперечные колебания бесконечной струны или продольные колебания
бесконечного стержня. Она является идеализацией той ситуации, когда
изучаемый объект действительно имеет значительные размеры и
рассматриваются процессы в тех его точках, которые удалены от его границ.
В этих случаях возможное
влияние граничных условий невелико и им
допустимо пренебречь.
5.2. Решение задачи
Известным образом (см. Лекция 2) уравнение (1) приводится к
каноническому виду и определяется его общее решение. Далее, производится
переход к первоначальным переменным и с использованием начальных
условий устанавливается окончательный вид функций, вошедших в общее
решение.
Рассмотрим эти этапы последовательно.
Приведение уравнения к каноническому виду. Составляем
уравнение характеристик
0)()(
222
=− dtadx ,
откуда
a
dt
dx
±= .
Интегрируя теперь последние соотношения имеем
C
a
t
x
= .
Положим
a
t
x
−=
ξ
, a
t
x
+=
η
.
и выразим
tt
u ,
xx
u через новые переменные
ξ
,
η
. Имеем
ηξ
uuu
x
+=
,
ηηξηξξηηηξξηξξ
uuuuuuuu
xx
++=+++= 2
,

64
ηξ
auauu
t
+−=
ηηξηξξηηηξξηξξ
uauauaauauaauauau
tt
222
2)()( +−=+−++−−=
.
Подставляя эти соотношения в уравнение (1), получаем
0=
ξη
u
. (3)
Общее решение. Рассматриваем (3). Проведя последовательное
интегрирование, имеем
0)( =
∂
∂
ξ
η
u
.
Следовательно,
)(
1
ξ
ξ
Fu =
,
где
)(
1
ξ
F
, - произвольная функция. Далее, интегрируя последнее
соотношение, имеем
ξξξ
ξ
dFd
u
)(
1
=⋅
∂
∂
,
)()(),(
η
ξ
η
ξ
G
F
u += , (4)
где
ξξξ
= dFF )()(
1
, )(
η
G
- произвольные функции. Соотношение (4) и
представляет собой общее решение уравнения (3). Выполняя обратную
замену переменных, получаем общее решение уравнения (1) в исходных
переменных
)()(),( a
t
x
G
a
t
x
F
t
x
u ++−= . (5)
Решение Даламбера. Воспользуемся начальными условиями (2) и
подберем вид функции F и G.
Имеем
)()()()0,(
x
x
G
x
F
x
u
ϕ
=+=
)()()()()0,(
0
xxaGxaFGFxu
tttt
ψ
η
ξ
ηξηξ
=+−=⋅+⋅=
=
.

65
Таким образом, для определения функции F и G имеем систему
уравнений
=+−
=+
)()()(
)()()(
xxaGxaF
xxGxF
ψ
ϕ
ηξ
.
Заметим, что в силу вида функций F и G справедливы соотношения
=
−
=
=
=
0
)(
)(
0
t
atxF
dx
d
d
dF
xF
t
ξ
ξ
=
+
=
=
=
0
)(
)(
0
t
atxG
dx
d
d
dG
xG
t
η
η
.
Поэтому последней системе уравнений можно придать вид
=
′
+
′
−
=+
)()()(
)()()(
xxGaxFa
xxGxF
ψ
ϕ
.
Дифференцируя теперь первое из уравнений имеем
=
′
+
′
−
′
=
′
+
′
=+
)()()(
)()()(
)()()(
xxGaxFa
xxGxF
xxGxF
ψ
ϕ
ϕ
, (6)
где последние два уравнения представляют линейную систему относительно
)(xF
′
, )(xG
′
. Разрешая её, получим
a
xxa
xG
2
)()(
)(
ψ
ϕ
+
′
=
′
a
xxa
xF
2
)()(
)(
ψ
ϕ
−
′
=
′
,
а после интегрирования на промежутке
[]
a;0, -
+−=−
+−=−
a
a
dxx
a
aFaF
dxx
a
aGaG
0
0
)(
1
)0(
2
1
)(
2
1
)0()(
)(
1
)0(
2
1
)(
2
1
)0()(
ψϕϕ
ψϕϕ
.
Подставляя теперь функции F, G с соответствующими аргументами в
соотношение (5) и, учитывая, что в силу первого из уравнений (6),
)0()0()0(
ϕ
=+
G
F ,
66
получим
+
−++
=
+
−
atx
atx
dxx
a
atxatx
txu )(
2
1
2
)()(
),(
ψ
ϕϕ
(7)
Выражение (7) и представляет собой
решение Даламбера задачи Коши
(1), (2). Оно может быть приспособлено и для решения краевых задач, в
частности, анализа колебаний струны конечной длины.
Рассмотрим в заключение пример, иллюстрирующий использование
формулы (7).
Задание. Найти отклонения бесконечной однородной струны при
следующих начальных условиях:
1. Известен профиль струны )(
x
ϕ
в момент 0=
t
2. Начальные скорости отсутствуют.
Решение. В данном случае задача Коши имеет вид
0 , ,
2
>+∞<<∞= tx-uau
xxtt
=
−∉
−∈
=
0)0,(
2
;
2
, 0
2
;
2
, cos
)0,(
xu
x
xx
xu
t
ππ
ππ
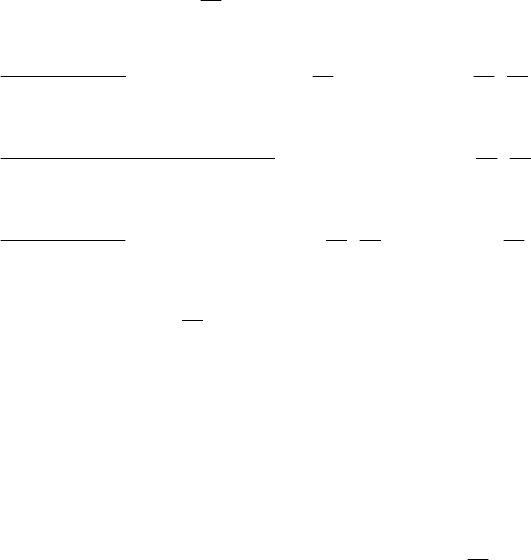
67
Здесь 0)( ≡
x
ψ
. Тогда, используя (7) и учитывая особенности функции
)(
x
ϕ
, имеем
>−
>+
−∈−
−
−∈±
−++
−∈+−<−
+
−<+
=
2
если , 0
2
,
2
;
2
если ,
2
)cos(
2
;
2
если ,
2
)cos()cos(
2
;
2
,
2
если ,
2
)cos(
2
если , 0
),(
π
πππ
ππ
πππ
π
atx
atxatx
atx
atx
atxatx
atxatx
atx
atx
txu
(8)
Заметим, что выше, при выводе формулы Даламбера, предполагалось
существование
)(x
ϕ
′
. Поэтому без дополнительного исследования решение
(8) можно считать обоснованным лишь в точках
2
π
±≠± atx
.
Лекция 6. Метод Фурье (применительно к решению одномерных
краевых задач)
6.1. Теоретические положения
Метод Фурье (или метод разделения переменных) является одним из
основных аналитических методов решения линейных краевых задач
гиперболического и параболического типов. В теоретическом плане он
обоснован для следующих задач:
0 , M ,)grad(
>∈−=
tDquuκdiv
u
u
t
tt
ρ
ρ
, (1)

68
где
=
=
)()0,(
)()0,(
MMu
MMu
t
ψ
ϕ
, D
M
∈ , (2)
>∈=
∂
∂
+
>∈=
∂
∂
>∈=
0 , , 0),(
0 , , 0
0 , , 0),(
tSM
n
u
tMu
tSM
n
u
tSMtMu
γ
. (3)
Здесь D – вообще говоря, n-мерная открытая область, ограниченная
кусочно-гладкой поверхностью S, коэффициенты уравнения (1)
удовлетворяют условиям
0)(,0)(,0)(
≥>>
M
q
M
k
M
ρ
,
где ),...,(
1 n
xxM = , а набор начальных (2) и вид граничных (3) условий
выбираются, соответственно, в зависимости от типа краевой задачи.
Согласно метода Фурье решение задачи (1)-(3), первоначально, ищется в
виде
)()(
t
T
M
Фu = , (4)
где
Ф(М), T(t), - непрерывно дифференцируемые, достаточное число раз,
функции своих переменных. Подставив (4) в (1), получаем
ТqФkgradФdiv
ТФ
ТФ
))(( −=
′
′′
ρ
ρ
или, после деления обеих частей на
Ф
T
ρ
, -
Ф
qФkgradФdiv
T
T
T
T
ρ
−
=
′
′′
)(
.

69
Левая часть последнего соотношения зависит только от
t
, правая, - от
x
1
, … , x
n
. Так эти переменные независимы, то каждая часть есть величина
постоянная. Обозначив её через
λ
− , в результате этого получим
−=
′
−=
′′
λ
λ
T
T
T
T
(5)
и
λ
ρ
−=
−
Ф
qФkgradФdiv
)(
(6)
Если выражение (4) подставить в граничные условия (3), получим
=
∂
∂
⋅+
=
∂
∂
=
0)(
0
0)(
n
Ф
MФ
n
Ф
MФ
γ
. (7)
Уравнение (6) совместно с условием (7), точнее, с одним из них,
называется
задачей Штурма-Лиувилля, её нетривиальные решения, -
собственными функциями, а соответствующие им значения λ, -
собственными значениями краевой задачи (1)-(3).
Фундаментальное значение для обоснования метода имеют следующие
утверждения.
Пусть
n
λ
,
N
n∈ , - собственные значения, а Ф
n
(М), - система
собственных функций. Заметим, что Ф
n
определяются с точностью до
постоянного множителя. Тогда справедлива
Теорема 1. Собственные значения краевой задачи (1)-(3)
неотрицательны, а их множество счетно.
70
Из (5), в этом случае, имеем
=
+=
− t
nn
nnnnn
n
eAT
tBtAT
λ
λλ
sincos
Тогда каждая из функций
)()(),( tTMФtMu
nnn
=
удовлетворяет как уравнению (1), так и граничным условиям (3). Теперь уже,
чтобы удовлетворить и начальным условиям (2) решение задачи ищется в
виде
∞
=
=
1
),(),(
n
n
tMutMu ,
т.е.
∞
=
⋅=
1
)()(),(
n
nn
tTMФtMu .
Положив теперь 0=
t
, имеем
=⋅
n
nn
MTMФ )()0()(
ϕ
=
′
n
nn
MTMФ )()0()(
ψ
Из этих соотношений и определяются наборы коэффициентов
n
A ,
n
B с
использованием ортогональности функции )(MФ
n
.
Замечание. Заметим, что задача (1)-(3) является однородной. Если же в
исходной задаче уравнение неоднородно, то эта неоднородность
раскладывается в ряд Фурье по собственным функциям соответствующей
Теорема 2. Система собственных функций ортогональна в области D с
весом ρ, т.е.
=
D
mn
dvMФMФM 0)()()(
ρ
, mn ≠ .
Каждая из функций непрерывно дифференцируемых в
D
разлагается в
ряд Фурье по собственным функциям
n
Ф . Этот ряд абсолютно и равномерно
сходится в
D
, где
D
- замыкание области D .
