Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.

41
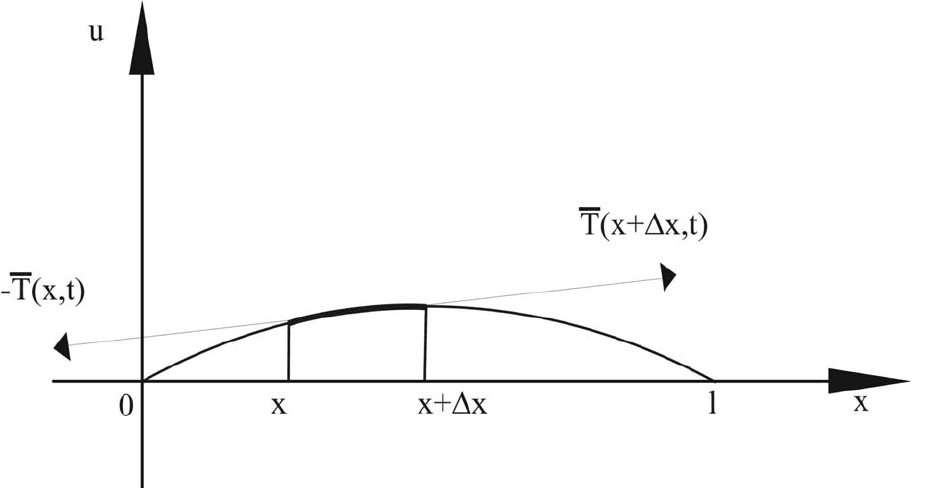
Рисунок 1. Малые поперечные колебания струны
Процедура составления уравнения состоит в следующем.
Рассматривается малый участок струны [x, x+Δx], (см. Рисунок 1),
описываются действующие на него силы и оставляется уравнение его
движения в направлении оси ou, как твердого тела. Далее, в полученном
соотношении осуществляется предельный переход при Δ x→ 0.
На
выделенный участок действуют следующие силы:
- силы натяжения
),(),,(
__
txTtxxT −+
Δ
, которые описывают действие
отброшенных частей струны на рассматриваемый участок;
- внешние силы, суммарная проекция которых в направлении оси
описывается линейной плоскостью ).,(
t
x
f
Силы натяжения обусловливаются растяжением струны. Принято
считать, что они направлены по касательным к профилю струны в
«противоположные» стороны. Далее, если принять, что
),(
_
txT
представляет
собой действие в точке x со стороны участка [x, l], то становится понятным и
заданные на Рисунке 1 знаки.

42
Подчеркнем, что в данном случае, рассматриваются малые колебания
струны. В математическом плане под этим понимают возможность
пренебрежения величинами порядка
22
,
x
uu . Эти допущения влекут
следующие особенности:
1.
сила натяжения
),(
_
txT
не зависит от х.
Действительно, из отсутствия перемещений в направлении oх следует,
что
0),(),((
__
=++− tхxTпрtxTпр
охох
Δ
Обозначим через
.),(),( txTtxT = Тогда, исходя из геометрического
смысла производной
).,()),(
2
1
1)(,(
),(1
1
),(cos),(),(
2
2
_
tхxTtxutхxT
txxu
txxTtхxTtхxTпр
x
x
ох
ΔΔ
Δ
ΔϕΔΔ
+=−+=
=
++
⋅+=+=+
).,()),(
2
1
1(),(
),(1
1
),()),((
2
2
_
txTtxutxT
txu
txTtxTпр
x
x
ох
−=−⋅=
+
⋅−=−
Таким образом
.0),(),( =++− txxTtxT
Δ
В силу произвольности значения х следует, что
).(),( tTtxT =
2.
сила натяжения )(
_
tT не зависит также и от
t
.
Действительно, длина струны
)(
t
l
в момент времени
t
равна

43
.),(
2
),(
2
1
),(
2
1
),(
2
1
1),(1)(
2
0
2
0
2
0
0
2
0
2
ltxu
l
ldxtxul
среднемо
теоремепо
dxtxudx
dxtxudxtxutl
x
l
x
l
x
l
l
x
l
x
=
+=+=
+
=
=
+=
+=
==
Таким образом, в процессе колебаний длина струны остается
постоянной, точнее, практически постоянной, следовательно, и
.)(
0
TtT =
Тогда необходимые для составления уравнения движения участка
проекции сил натяжения на ось ou равны
).,(
1
sin),(
0
2
0
0
_
tхxuT
u
u
TTtхxTпр
x
x
x
ох
ΔϕΔ
+=
+
==+
),,(),((
0
txuTtxTпр
xох
−=−
а проекции внешних сил, -
.),(
х
t
x
f
Δ
Обозначив теперь через
)(
x
ρ
линейную плотность материала струны,
согласно второго закона Ньютона имеем
{}
.),(),(),()(
0
xtxftxutxxuTuxx
xxtt
Δ
Δ
Δ
ρ
+−+=⋅
Разделим теперь эти части соотношения на
х
Δ
и перейдем к пределу при
.0→
х
Δ
Получим
).,()(
0
txfuTux
xxtt
+=
ρ
Или
),,(
2
txFuau
xxtt
+=
(1)
где
).(/),(),(),(/
2
xtxftxFxTa
o
ρρ
==
Если струна однородная, т.е.
0
)(
ρ
ρ
=x
, то очевидно, коэффициент
2
a
также является константой.
44
Уравнение (1) является искомым, оно и описывает колебания точек
струны при сделанных предложениях. Нередко оно называется
одномерным
волновым уравнением.
3.2. Продольные колебания стержня
Рассмотрим упругий стержень (Рисунок 2) длины l с поперечным
сечением S(x) и модулем Юнга
).(
x
F
Предположим, что точки одного
сечения совершают одинаковые движения и обозначим через
),(
t
x
u
отклонение в продольном направлении в момент времени
t
, сечение, которое
в ненапряженном состоянии имеют абсциссу
x
.
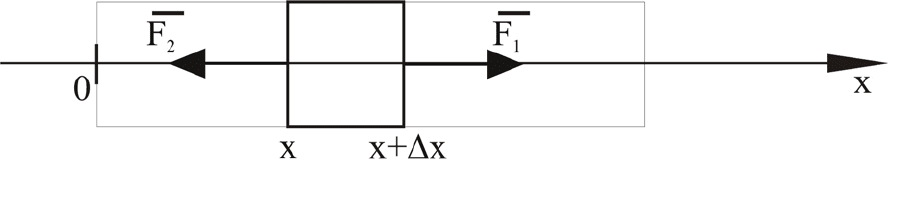
Рисунок 2. Продольные колебания стержня
Составим уравнение относительно функции
),(
t
x
u
предполагая наличие
внешней силы с заданной линейной плотностью
),(
t
x
f
.
Как и выше (см. п. 1) процедура получения уравнения остается прежней.
А именно, рассматривается достаточно малый участок [x, x+Δx] стержня,
описываются действующие на него силы и составляется уравнение его
движения как твердого тела. Далее, через предельные переходы при
0→
х
Δ
приходят к требуемому уравнению.
Предположим, что
х
Δ
достаточно мало. В этом случае выделенный
участок полностью расположен в зоне деформации одного типа (или
растяжения, как на рисунке 1, или сжатия). Поэтому действующие на участок
силы, обусловленные напряжениями внутри стержня, направлены в

45
противоположные стороны. Далее, допустим, что напряжения, возникающие
в стержне в процессе деформации, подчиняются закону Гука. В этом случае
силы со стороны удаленных частей стержня описываются выражениями
).,()()(
),,()()(
2
1
txuxSxEF
txxuxxSxxEF
x
x
−=
+++=
Δ
Δ
Δ
Тогда, в соответствии со вторым законом Ньютона имеем
−+++=⋅ ),()()()( txxuxxSxxEuxx
xtt
Δ
Δ
Δ
Δ
ρ
,),(),()()( xtxftxuxSxE
x
Δ
+−
где, )(
x
ρ
, - линейная плотность стержня. После деления на
x
Δ
и
предельного перехода при 0→
x
Δ
, получим уравнение.
),,()),()()(()( txftxuxSxE
x
ux
xtt
+
∂
∂
=
ρ
которое и является искомым. Если предположить, что
S
E
,,
ρ
- постоянные,
то обозначив
ρρ
),(
),(,
2
txf
txF
ES
a ==
, получим знакомое волновое
уравнение
(см. п. 1).
).,(
2
txFuau
xxtt
+=
Таким образом, как поперечные колебания однородной струны, так и
продольные колебания однородного стержня описываются внешне
одинаковыми уравнениями.
3.3. Малые поперечные колебания мембраны
В данном контексте
мембраной называется тонкая упругая пленка, не
оказывающая сопротивления изгибу.
46
Задача формулируется следующим образом. Предварительно натянутая
мембрана тем или иным образом, закреплена вдоль некоторого контура
G,
расположенного в плоскости
xoy. Необходимо составить уравнение,
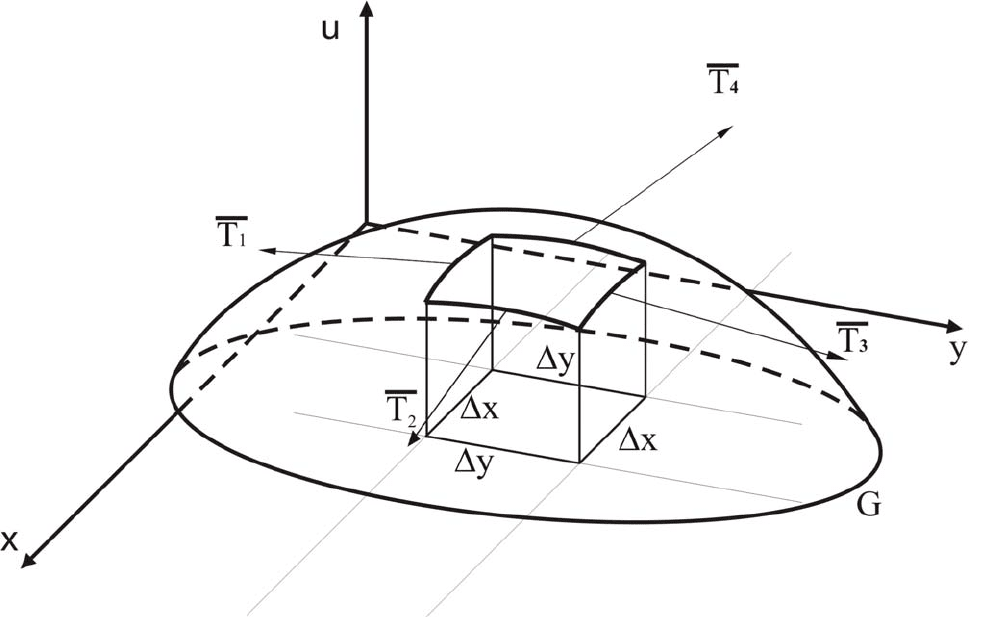
описывающее малые колебания ее точек этой плоскости (Рисунок 3).
Рисунок 3. Колебания мембраны
Обозначим через ),,(
t
y
x
u отклонение от плоскости xoy точки мембраны,
проекция которой на плоскость
xoy есть точка ),( y
x
. Вследствие малости
рассматриваемых движений будем пренебрегать при выводе уравнения
малыми второго порядка
222
,,
yx
uuu и т.д.
Рассечем мембрану плоскостями параллельными координатным
плоскостям
xou, you и выделим малый участок (см. Рисунок 3).
47
Предположим, что его проекцией на плоскость xoy является
прямоугольник ].,;,[
yyy
x
x
x
Δ
Δ
++ Составим уравнение движения этого
участка как твердого тела.
В силу отсутствия «изгибных» сопротивлений предполагается, что силы
натяжения действуют в плоскостях касательных к профилю мембраны
перпендикулярно границе выделенного участка. Можно показать, что
малость рассматриваемых перемещений и их отсутствие в плоскости
параллельной плоскости
xoy влечет постоянство величины сил натяжения.
Обозначим через
0
T линейную плотность этих сил. Тогда распределение сил
натяжения показано на Рисунке 3, где
xTTT
Δ
031
==
.
042
yTTT
Δ
==
Проекции же этих сил на направления
ou соответственно равны
),,(
01
_
tyхuxTTпр
yоu
⋅Δ−=
),,(
03
_
tyyхuxTTпр
yоu
ΔΔ
+⋅=
),,(
02
_
tyхxuyTTпр
xоu
ΔΔ
+⋅=
).,,(
04
_
tyxuyTTпр
xоu
⋅−=
Δ
Пусть, далее, задана плотность внешних сил
),,(
t
y
x
f
. Здесь
учитывается, что с точностью до малых второго порядка
22
,
yx
uu площадь
рассматриваемого участка равна площади его проекции на
xoy.
Применяя теперь второй закон Ньютона, имеем
)),,(),,((),(
0
tyxutyyxuxTuyxyx
yytt
−+=⋅⋅
Δ
Δ
Δ
Δ
ρ
.),,(
)),,(),,((
0
yxtyxf
tyxutyxxuyT
xx
ΔΔ
Δ
Δ
⋅+
−++
.

48
Деля теперь, обе части последнего соотношения на
y
x
Δ
Δ
⋅
и переходя к
пределу при
0, →y
x
Δ
Δ
получаем
),,()(),(
0
tyxfuuTuyx
yyxxtt
++=
ρ
или
),,,(
2
tyxFuau
tt
+⋅=
Δ
(2)
где
),(
),,(
),,(
yx
tyxf
tyxF
ρ
=
,
,
),(
0
2
yx
T
a
ρ
=
yyxx
uuu +=
Δ
- двумерный оператор Лапласа.
Для однородной мембраны
0
),(
ρ
ρ
=yx
и величина
2
a
является
постоянной.
Уравнение (2)описывают колебания мембраны, при указанных
предположениях, имеет гиперболический тип и называется
двумерным
волновым
уравнением.
3.4. Уравнение теплопроводности (диффузии)
Уравнение теплопроводности описывает распространение тепла в среде.
Рассмотрим трехмерный случай. Пусть поверхность
S ограничивает
некоторый объем
V (твердое тело, газ, жидкость). Обозначим через
),(
t
M
u
- температуру в точке
М этого объема в момент времени
t
. Уравнение для
),(
t
M
u
составляется на основании уравнения теплового баланса:
21
,,,, QSьповерхност
черезпрошедшее
теплаколичество
Qтела
ытемпературизменениена
ушедшеетеплаколичество
QtвремязаV
объемеввыделенное
теплаколичество
+=
Δ
т.е.
21
QQQ +=
.
Опишем каждую из этих составляющих.

49
1. Пусть
),(
t
M
f
- объемная плотность источников выделения
(поглощения) тепла.
Тогда
tdvtMfQ
V
Δ
= ),(
.
2.
Пусть
)(
M
c
представляет собой удельную теплоемкость среды,
)(
M
ρ
, - ее объемная плотность. Тогда
=
V
dvMtMctMuQ )(),(),(
1
ρ
Δ
3.
Для описания потока тепла через поверхность используем закон
Фурье. Согласно ему количество тепла, проходящее через единицу площади
в направлении нормали участка
_
n за единицу времени равно
n
u
kq
∂
∂
⋅−=
,
где )(
M
k , коэффициент теплопроводности. Будем считать, что
_
n - вектор
внешней нормали. Тогда
tds
n
u
kQ
S
Δ
∂
∂
−=
2
.
Учтем, далее известное соотношение
γβα
coscoscos
_
z
u
y
u
x
u
nugrad
n
u
∂
∂
+
∂
∂
+
∂
∂
=⋅=
∂
∂
,
где
)cos,cos,(cos
_
γβα
=n
и для приведения поверхностного интеграла к
объемному воспользуемся теоремой Острорадского – Гаусса:
=⋅
SV
dvadivdsna
___
.
В результате этого получим
tdv
g
radukdivQ
V
Δ
..
−=
)(
2

50
Подставим теперь полученные в 1-3 соотношения в уравнение теплового
баланса.
Имеем
tdvkgradudivdvMMctMutdvtMf
VVV
ΔρΔΔ
−
=
)()()(),(),(
.
Перенесем все выражения в одну часть, разделим на
t
Δ
и перейдем к
пределу при
0→
t
Δ
. Имеем
0),()( =
−−
∂
∂
V
dvtMfugradkdiv
t
u
c
ρ
Заметим, что данное соотношение справедливо для произвольного
объема V, поэтому подинтегральная функция должна быть равна нулю.
Отсюда
),()( tMfugradkdiv
t
u
c +−
∂
∂
ρ
(3)
Это уравнение есть искомое, оно называется уравнением
теплопроводности.
Отметим, что оно параболического типа.
В частном случае, когда
k
c ,,
ρ
- постоянны, и учитывая, что
uuuuugraddiv
zzyyxx
Δ
=++=)(, получим
),(
2
tMFua
t
u
+=
∂
∂
Δ
,
где .
),(
),(,
2
ρρ
c
tMf
tMF
c
k
a ==
Замечание 1. Аналогичным образом, выводится и уравнение,
описывающее концентрацию вещества, оно называется
уравнением
диффузии
.
В этом случае ),(
t
M
u представляет концентрацию диффундирующего
вещества, а вместо закона Фурье используется закон Нернста
,
n
u
Dq
∂
∂
−=
