Лекции - Краевые задачи математической физики
Подождите немного. Документ загружается.

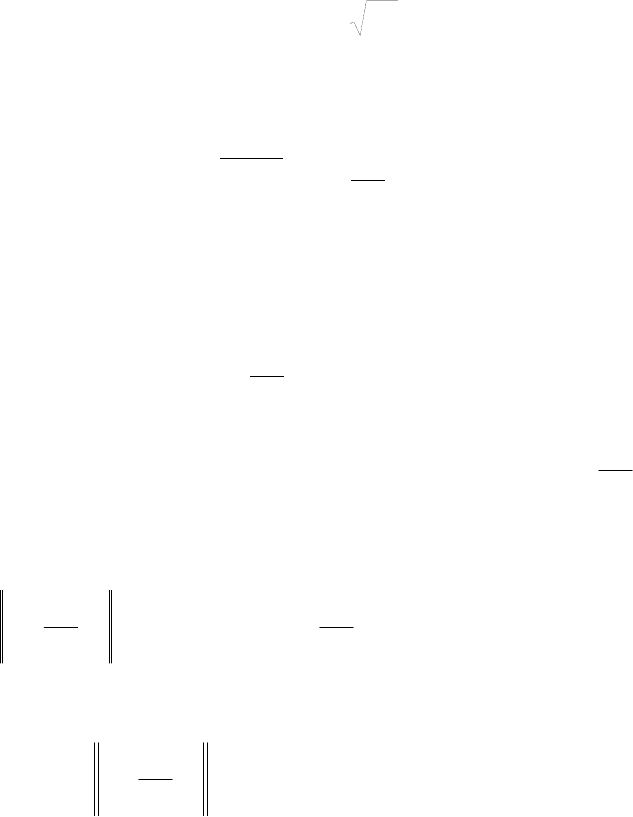
91
07 =+
′
nnn
TT
λ
,
откуда
t
nn
n
eAT
λ
7−
=
.
Тогда, в соответствии с общей схемой метода Фурье, решение краевой
задачи (16), (17), (18) ищем в виде ряда
⋅=
∞
=
−
1
0
7
)(),(
n
n
t
n
rIeAtru
n
λ
λ
или
⋅=
∞
=
−
1
0
16
7
4
),(
2
n
n
t
n
rIeAtru
n
μ
μ
.
Для определения коэффициентов
n
A воспользуемся начальным условием.
Имеем
−=
=
∞
=1
2
0
16
4
)0,(
n
n
n
rrIAru
μ
Умножим теперь обе части последнего соотношения на
rrI
n
4
0
μ
и
почленно проинтегрируем на
]4;0[ . Имеем
drrIrrrIA
nn
n
−=
⋅
4
0
0
2
2
0
4
)16(
4
μμ
. (30)
Используя соотношение (29), получим
)(8
4
2
0
2
0 n
n
IrI
μ
μ
′
=
. (31)
Попытаемся теперь вычислить или, по крайней мере, упростить
интеграл, расположенный в правой части соотношения (30), приведя его к
конечному виду.
Прежде всего учтём, что из уравнения (25) при 0=
ν
, в частности,
следует
0)()()(
0
2
00
2
=+
′
+
″
zIzzzIzIz
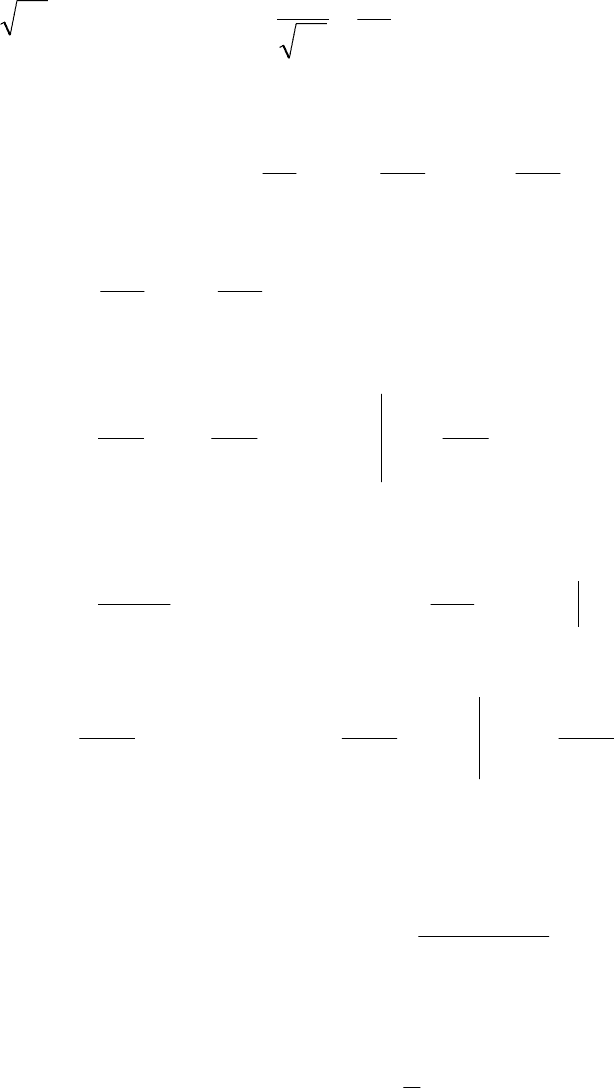
92
Или, после сокращения на z ,
)()()(
000
zzIzIzzI −=
′
+
″
Отсюда
(
)
)()(
00
zzIzIz −=
′
′
. (32)
Тогда после выполнения замены в рассматриваемом интеграле
zr
n
=
λ
(или
z
z
r
n
n
μ
λ
4
==
), последовательного использования
соотношения (32) и интегрирования по частям, получим
=
−=
−=
4
00
)32(
0
2
22
0
2
)(
1
1
16
4
)16(
n
dzzIzzdrrIrrI
nn
n
μ
μμ
μ
(
)
частям по
0
0
2
22
2
)(
1
1
16
=
′
′
−−=
dzzzIz
n
nn
μ
μμ
=
′
+
′
−−=
n
n
dzzIzzzIz
nnn
μ
μ
μμμ
0
0
2
2
0
0
0
2
22
2
)(
2
)(
1
1
16
=
−−=
′
⋅
−=
nn
n
dzzIzzIzdzzIz
nn
μμ
μ
μμ
0
)32(
0
0
0
0
0
2
4
частям по
0
2
4
2
)(2)(
512
)(
216
(
)
′
−=
′
−=
′
′
=
n
n
n
nnn
IzzIdzzzI
μ
μ
μ
μμμ
0
0
3
0
0
4
0
4
)(
1024
)(
1024
)(
1024
. (33)
Таким образом, из (30) с учётом (31), (33) имеем
)(
128
0
3
nn
n
I
A
μμ
′
⋅
−= .
Если же теперь дополнительно использовать свойство
)()()(
1
zIzI
z
zI
+
−=
′
ννν
ν

93
при 0=
ν
, окончательно получим
)(
128
1
3
nn
n
I
A
μμ
⋅
= .
Таким образом, решение данной краевой задачи имеет вид
∞
=
−
⋅
⋅
⋅=
1
0
16
7
1
3
4
)(
1
128),(
2
n
n
t
nn
rIe
I
tru
n
μ
μμ
μ
,
где
n
μ
- корни уравнения 0)(
0
=zI .
7.3. Эллиптическая задача (в круговой области)
Задание. Решить задачу Дирихле для уравнения Лапласа в круге
0=Δu , 30 <≤
r
πϕϕ
2
3
2
+−=
=
r
u
. (34)
Решение. Из постановки задачи вытекает целесообразность
использования полярных координат. Поэтому, для начала, представим
уравнение Лапласа в полярных координатах. Имеем
22
yxr +=
,
x
y
tg =
ϕ
.
Тогда, непосредственно дифференцируя первое соотношение и второе, - как
неявно заданную функцию, получим
r
x
x
r
=
∂
∂
,
r
y
y
r
=
∂
∂
,
2
r
y
x
−=
∂
∂
ϕ
,
2
r
x
y
=
∂
∂
ϕ
.
Далее, находим вторые производные:
2
2
2
2
r
y
x
r
=
∂
∂
,
3
2
r
xy
yx
r
−=
∂∂
∂
,
3
2
2
2
r
x
y
r
=
∂
∂
,
42
2
2
r
xy
x
−=
∂
∂
ϕ
,
4
222
r
yx
yx
−
−=
∂∂
∂
ϕ
,
42
2
2
r
xy
y
=
∂
∂
ϕ
.
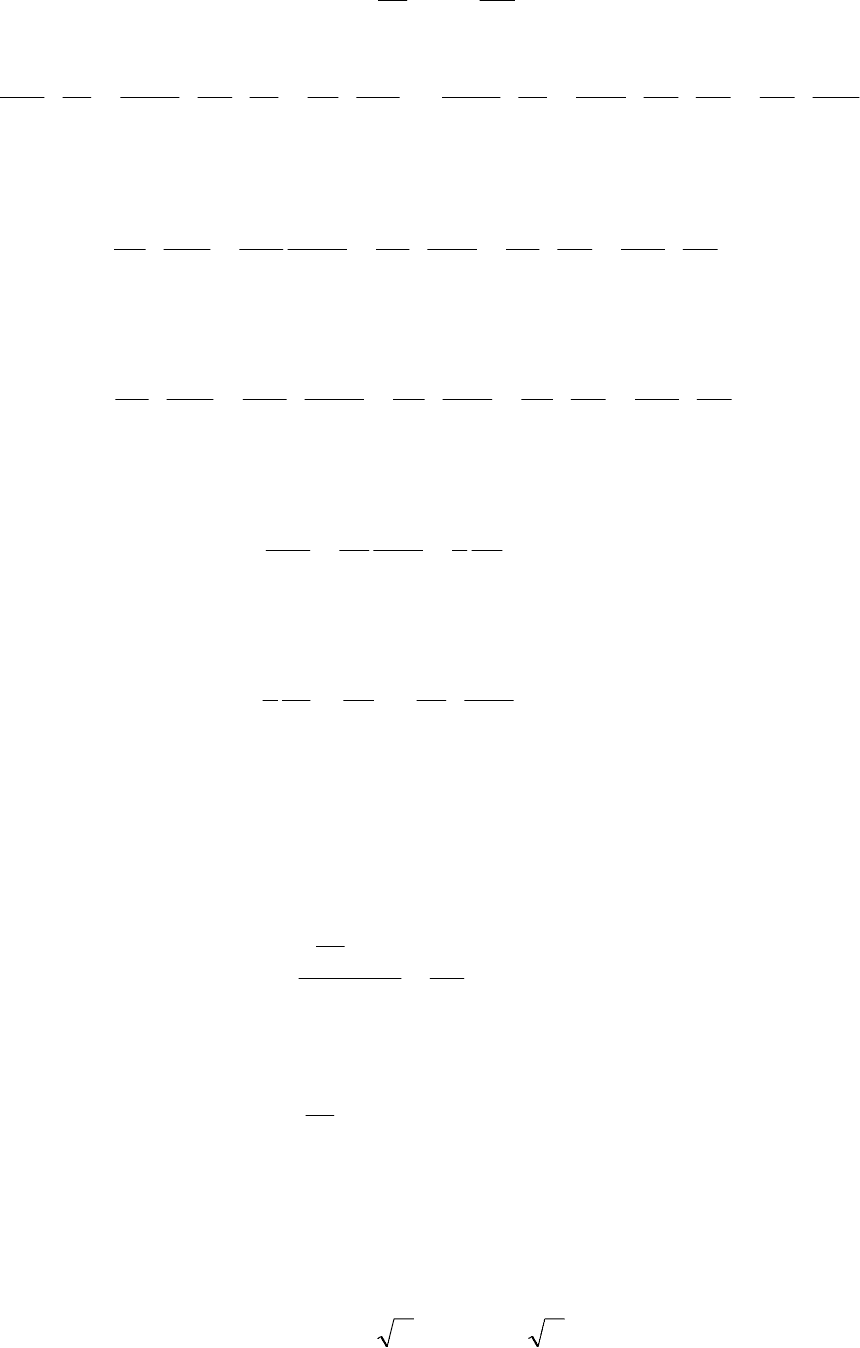
94
Тогда
x
u
x
r
uu
rx
∂
∂
⋅+
∂
∂
⋅=
ϕ
ϕ
,
2
2
2
22
2
22
2
2
x
u
xx
u
x
r
r
u
x
r
r
u
x
r
xr
u
x
r
r
u
u
xx
∂
∂
⋅
∂
∂
+
∂
∂
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
∂
∂
⋅
∂∂
∂
+
∂
∂
⋅
∂
∂
=
ϕ
ϕ
ϕϕ
ϕ
ϕ
ϕ
ϕ
,
или, подставляя полученные выше выражения
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
⋅−
∂
∂
⋅+
∂
∂
⋅+
∂∂
∂
−
∂
∂
⋅=
u
r
xy
r
r
yu
r
y
r
u
r
xy
rr
x
u
xx
43
2
2
2
4
22
32
2
2
2
22
. (35)
Действуя совершенно аналогичным образом, получим
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
⋅+
∂
∂
⋅+
∂
∂
⋅+
∂∂
∂
⋅+
∂
∂
⋅=
u
r
xy
r
r
xu
r
x
r
u
r
xy
rr
y
u
yy
43
2
2
2
4
22
32
2
2
2
22
. (36)
Тогда, согласно (35), (36) решаемое уравнение принимает вид
0
11
2
2
22
2
=
∂
∂
+
∂
∂
+
∂
∂
r
u
r
u
rr
u
ϕ
или
0
11
2
2
2
=
∂
∂
⋅+
∂
∂
∂
∂
ϕ
u
r
r
u
r
rr
(37)
Решение задачи (34), (37) ищем в виде
)()(),(
ϕ
ϕ
Ф
r
R
r
u = , (38)
Подставив (38) в (37), после разделения переменных получим
()
λ
−=
′′
=
′
∂
∂
−
Ф
Ф
R
Rr
r
r
.
Отсюда
=+
′′
=−
′
∂
∂
⋅
0
0)(
ФФ
RRr
r
r
λ
λ
. (39)
Здесь, очевидно, 0≥
λ
, т.к. )(
ϕ
Ф , -
π
2-периодическая функция. Решая
второе из уравнений (39), имеем
ϕλϕλϕ
sincos)(
21
CCФ += ,
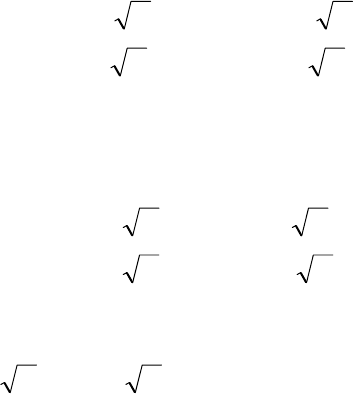
95
и из требования )()2(
ϕ
π
ϕ
ФФ =+ , учитывая произвольность постоянных
1
C ,
2
C имеем
=+
=+
ϕλπϕλ
ϕλπϕλ
sin)2(sin
cos)2(cos
.
Сворачивая выражения в каждом из соотношений в произведение,
имеем
=+⋅
=+⋅
0)cos(sin
0)sin(sin
λϕπλπ
λϕπλπ
.
Отсюда
0sin =
λπ
, n
πλπ
= ,
2
n
n
=
λ
, }0{∪∈
N
n .
Тогда
ϕ
ϕ
ϕ
nBnAФ
nnn
sincos)( += , (40)
где
N
n ∪∈ }0{.
Вернёмся к первому из уравнений (39). Имеем
0
22
=−
′
+
″
nnn
RnrRRr . (41)
Данное уравнение является
уравнением Эйлера. Возможны
следующие варианты его решения:
1.
замена
t
e
r
= , в результате которой получаем уравнение с постоянными
коэффициентами;
2.
α
rrR =)(, где
α
- постоянная.
Воспользуемся вторым вариантом. Из (41) имеем
0)1(
2
=−+−
ααα
ααα
rnrr
или
0
22
=− n
α
.
Отсюда n±=
α
. Таким образом, общее решение уравнения имеет вид
nn
rCrCR
−
+=
21

96
Но, в силу ограниченности и непрерывности решения в круге 3≤
r
,
имеем
0
2
=C . Таким образом,
n
n
rR =
)sincos(),(
ϕϕϕ
nBnArru
nn
n
n
+=
и
∞
=
+=
0
)sincos(),(
n
nn
n
nBnArru
ϕϕϕ
.
Далее, из граничного условия (34) имеем
∞
=
+−=+
0
2
2)sincos(3
n
nn
n
nBnA
πϕϕϕϕ
.
Заметим, что при 0=n естественно считать 0
0
=B . Умножая, теперь,
последовательно обе части на
ϕ
ncos
,
ϕ
nsin
и почленно интегрируя на
]2,0[
π
получим
ϕϕπϕϕϕϕ
ππ
dndnA
n
n
cos)2(cos3
2
0
2
0
22
−−=⋅ ,
ϕϕπϕϕϕϕ
ππ
dndnB
n
n
sin)2(sin3
2
0
2
0
22
−−=⋅
.
Отсюда, после интегрирования по частям,
3
20
3
0
π
=A
,
n
n
n
A
3
4
2
⋅
−= ,
n
n
n
B
3
4
3
⋅
−= ,
N
n∈ .
Таким образом, окончательно решение задачи имеет вид
−−=
∞
=1
2
3
sin
1
cos
3
4
3
20
),(
n
n
n
n
n
n
n
r
ru
ϕϕ
π
ϕ
.

97
Лекция 8. Метод функций Грина
Этот метод, наряду с методом Фурье, относится к числу основных
методов решения линейных задач математической физики. Его идея
заключается в следующем. Предварительно рассматривается некоторая
специальная задача, характерная для целого класса, и ищется её решение,
называемое функцией Грина. Далее, решение исходной задачи выражается
через функцию Грина с помощью квадратур.
Рассмотрим метод
на примере простейших задач параболического
типа.
8.1. Краевая задача
Пусть имеется однородная задача
=
∂
∂
+
=
><<=
=
0
),(
),(
)()0,(
0 ,0 ,
;0
2
lx
xxt
x
txu
htxu
xxu
tlxuau
ϕ
(1)
Рассмотрим дополнительную задачу
=
∂
∂
+
−=
><<=
=
0),(
)()0,(
0 ,0 ,
;0
2
lx
xxt
x
v
htxv
xxv
tlxvav
ξδ
(2)
где )(
ξ
δ
−
x
, —
δ
-функция Дирака. Напомним (см. Лекция 7), что
≠
=∞+
=−
ξ
ξ
ξδ
x
x
x
,0
,
)(
и обладает свойством

98
+∞
∞−
=− )()()(
ξξδ
gdxxxg . (3)
Предположим, что решение задачи (2) известно, обозначим его через
),,(
t
x
G
ξ
. Оно называется функцией Грина краевой задачи (1). Тогда
решение исходной задачи, т.е. задачи (1), определяется соотношением
ξξϕξ
dtxGtxu )(),,(),(
0
= . (4)
Попробуем обосновать этот факт, допуская возможность
дифференцирования под знаком интеграла. Действительно, подставив (4) в
(1), имеем
=
ll
xxt
dtxGadtxG
00
2
)(),,()(),,(
ξξϕξξξϕξ
или
()
=−
l
xxt
dtxGatxG
0
2
0)(),,(),,(
ξξϕξξ
.
Равенство, очевидно, верное, т.к. ),,(
t
x
G
ξ
является решением
уравнения (2). Следовательно, и функция (4) удовлетворяет уравнению (1).
Также, очевидным образом, выполняется начальное
=−==
ll
xdxdxGxu
0
)3(
0
)2(
)()()()()0,,()0,(
ϕξξϕξδξξϕξ
,
и граничные
0)(
),,(
),,(
;0
0
=
∂
∂
+
=
ξξϕ
ξ
ξ
d
x
txG
htxG
lx
l
условия.
Нахождение функции Грина в данном случае может быть выполнено с
помощью метода Фурье. Так, формально применяя его схему к решению
задачи (2), имеем:
1. Задача Штурма-Лиувилля
0)()( =+
′′
xXxX
λ
, 0≥
λ
.
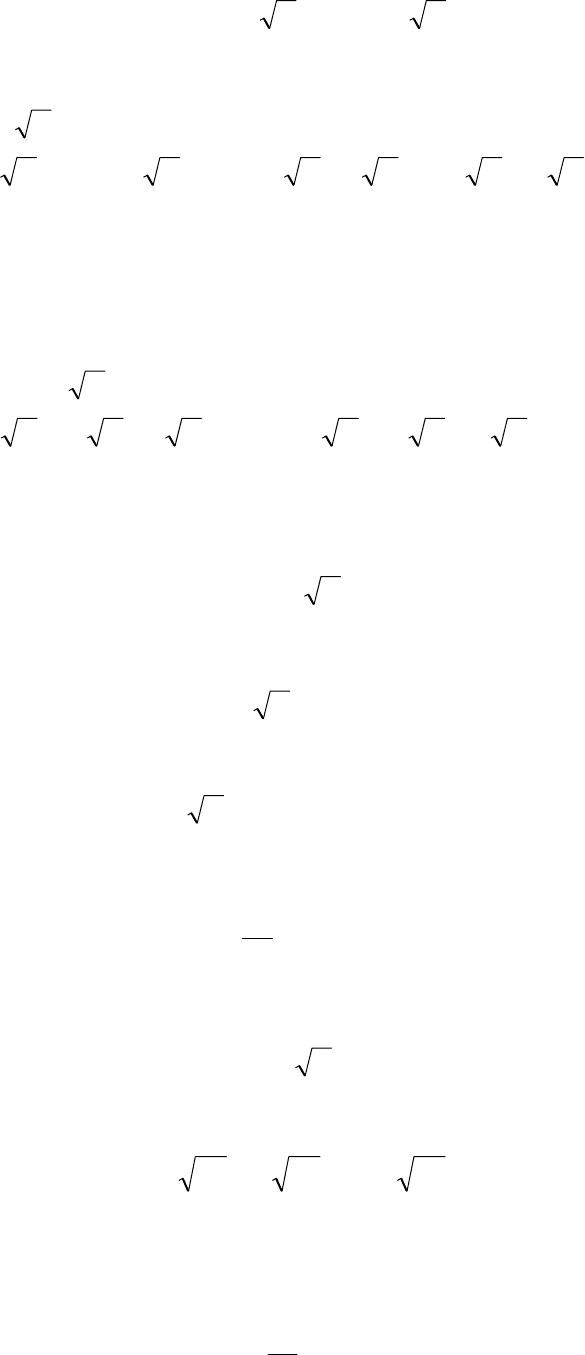
99
Отсюда
xCxCxX
λλ
sincos)(
21
+=
.
2. из граничных условий следует, что
=+−++
=⋅+
0)cossin(sincos
0
2121
21
lClChlClC
hCC
λλλλλλ
λ
.
Если 0=
λ
, то 0
1
=C и соответствующая функция 0≡X . Поэтому
0≠
λ
и, группируя слагаемые, получаем однородную систему уравнений
относительно С
1
, С
2
=++−
=⋅+
0)cos(sin)sin(cos
0
21
21
ClhlClhl
hCC
λλλλλλ
λ
.
Для нахождения ненулевых решений приравниваем к нулю
определитель системы, в результате чего получим
0sin)1(
2
=+ lh
λλ
.
Так как 01
2
>+
λ
h , то
0sin =l
λ
,
отсюда
nl
πλ
= ,
N
n ∈
или
2
=
l
n
n
π
λ
,
N
n ∈ .
Таким образом
nn
ChC
21
λ
−=
и собственные функции
xxhxX
nnnn
λλλ
sincos)( +−= , (5)
где постоянные
n
C
2
приняты равными единице.
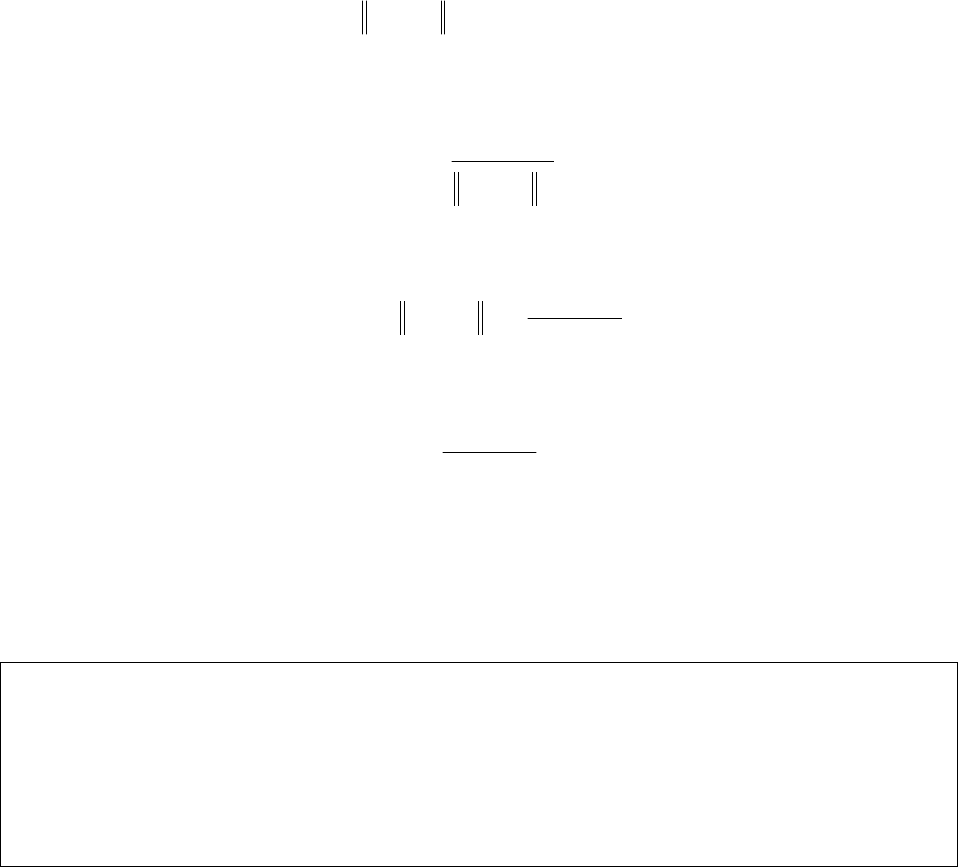
3. набор функций )(tT
u
t
l
na
nu
eAtT
2
)(
−
=
π
(6)
100
4. общий вид решения задачи (2)
∞
=
=
1
)()(),,(
n
nn
tTxXtxG
ξ
.
5. из начального условия
∞
=
−==
1
)()()0,,(
n
nn
xxXAxG
ξδξ
.
Отсюда
−=
l
nnn
dxxXxxXA
0
2
)()()(
ξδ
и
)(
)(
1
2
ξ
n
n
n
X
xX
A =
,
где
2
1
)(
2
2
n
n
h
xX
λ
+
= .
7. окончательное решение задачи (2)
+
= )()()(
1
2
),,(
2
ξ
λ
ξ
nnn
n
XxXtT
h
txG ,
где
)(tT
n
,
)(xX
n
,
)(
ξ
n
X
определяются соотношениями (5), (6).
Заметим, что аналогичным образом может быть введена и определена
функция Грина и для неоднородных краевых задач.
Замечание. В физическом плане функция ),,(
t
x
G
ξ
описывает эффект
наличия в точке
ξ
=
x
в момент 0=
t
некоторого источника. Поэтому иногда
она и называется
функцией влияния мгновенного точечного источника
или просто,
функцией влияния.
8.2. Задача Коши
Рассмотрим задачу
