Лекции - коллоидная химия
Подождите немного. Документ загружается.

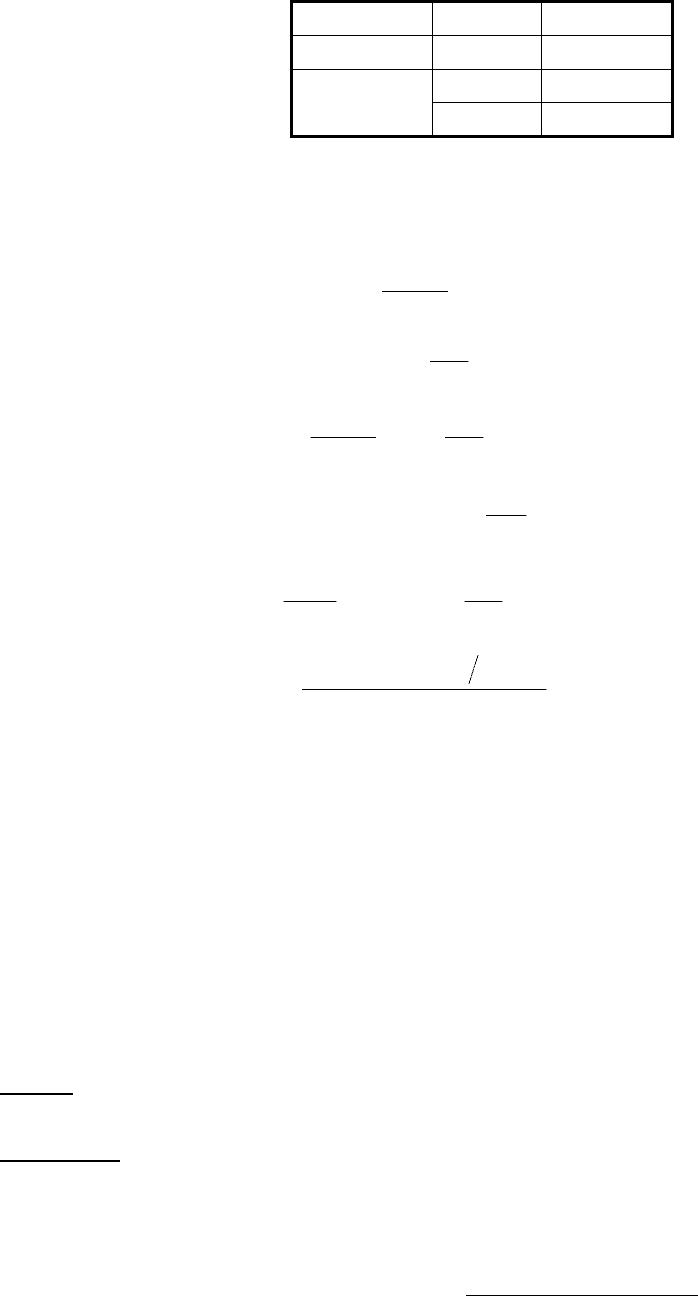
21
Размер частиц влияет на распределение по высоте:
Таблица 2.2
r, см h
½
O
2
в атм. 3·10
-8
5 км
2·10
-7
215 см
золь Au
2·10
-5
2·10
-5
см
Седиментационно-диффузионное равновесие частиц
произвольной формы в центробежном поле
2
cед
mx
iC
B
ω
=
(2.50)
диф
dC
iD
dx
=−
(2.51)
2
mx dC
C
kT dx
ω
=−
(2.52)
с учетом вытесняющей силы
NMm
d
d
mm
ч
ч
ж
ч
/;1 =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−= ,
22
11
2
xC
xC
mdC
xdx
kT C
ω
=−
∫
∫
(2.53)
(
)
()
()
12
22 2
21
2ln
ч
чж
RTd C C
M
x
xdd
=
ω− −
(2.54)
2.4. Осмотическое давление золей
Вводим понятия:
1)
частичная концентрация n (аналог числа молекул) в единице объема;
2)
грамм-частичная концентрация (аналог числу молей) ν = n/N
A
.
Тогда осмотическое давление рассчитывается:
π = νRT (2.55)
Найдем осмотическое давление для коллоидного раствора на примере:
Дано: 0,1% Au-золь, частицы – куб, l = 10
-6
см, d
Au
= 20 г/см
3
π – ?
Решение:
1) m
ч
= v
ч
·d
ч
; m
ч
= 10
-18
·20 = 2·10
-17
г.
2) n – ? 1000 г золя – 1 г Au ⇒ n = 0.5·10
17
частиц
3) ν = 0.5·10
17
/6,02·10
23
≈ 10
-7
моль
4) π = 10
-7
·RT ≈ 22.4·10
-7
атм. (или 0,02 мм. водного столба)
22
Осмотическое давление π очень мало! По этой причине метод не
используется для лиофобных золей.
Вторая причина. Осмотическое давление зависит от размеров частиц
(~ 1/r
3
):
⎟
⎠
⎞
⎜
⎝
⎛
π==
π
π
чч
drm
r
r
3
3
1
3
2
2
1
3
4
Для лиофобных золей r самопроизвольно увеличивается (агрегация
частиц). Таким образом осмотическое давление со временем меняется.
Осмотическое давление растворов ВМС
Осмотическое давление растворов ВМС выше чем для лиофобных
коллоидов вследствие их меньшего размера, достижимости больших
концентраций. Помимо этого, подвижные сегменты макромолекул выступают в
роли частиц, создающих давление.
а) Зависимость от концентрации:
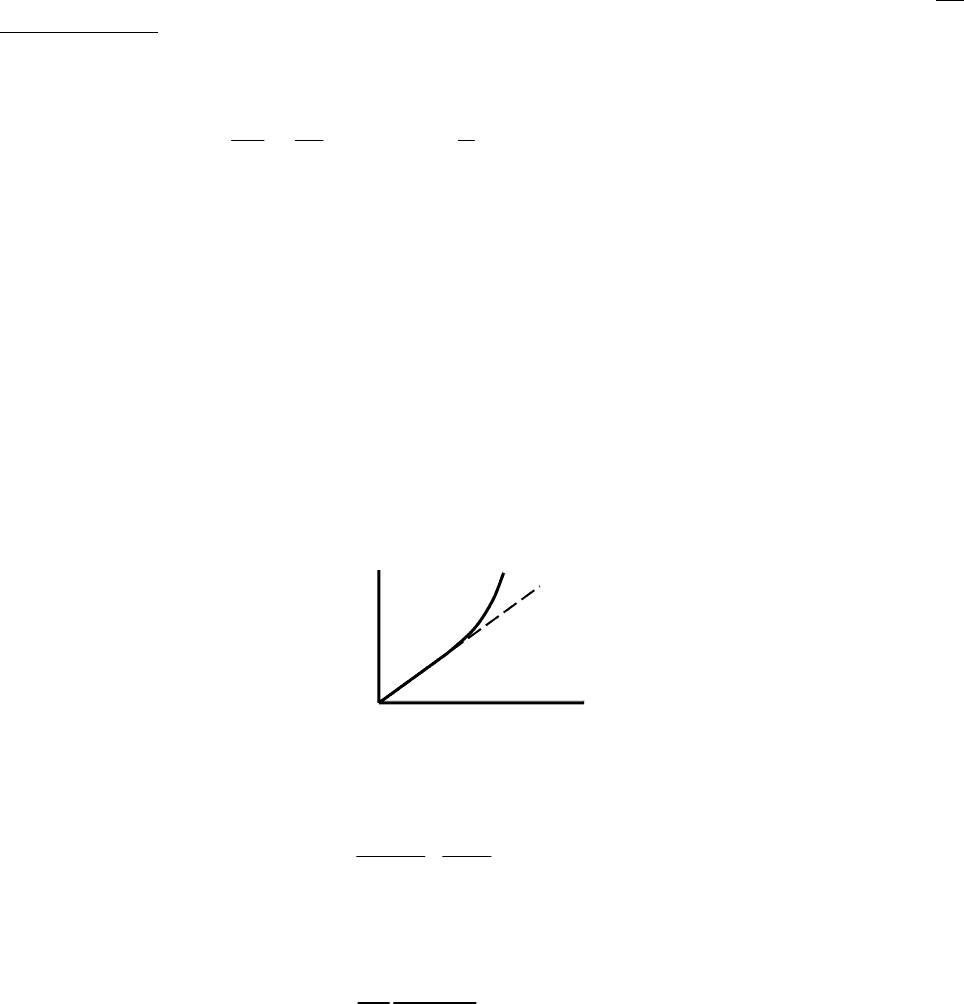
π = CRT для разбавленных растворов. При повышении концентрации
наблюдается отклонение от этой зависимости:
Рис. 2.10. Зависимость осмотического давления ВМС от концентрации.
Увеличение осмотического давления π по сравнению с теоретическим,
связано с сольватацией ВМС (часть растворителя несвободна).
ВМС
ВМС р-ля
mRT
M
V
⎛⎞
π=
⎜⎟
⎝⎠
(2.56)
– для истинных растворов, а для ВМС – поправка на объем связанного
растворителя:
()
mRT
M
Vb
π=
−
(2.57)
π
C
факт. –

23
б) Зависимость от температуры:
π
T
M
2
M
1
t
1
t
2
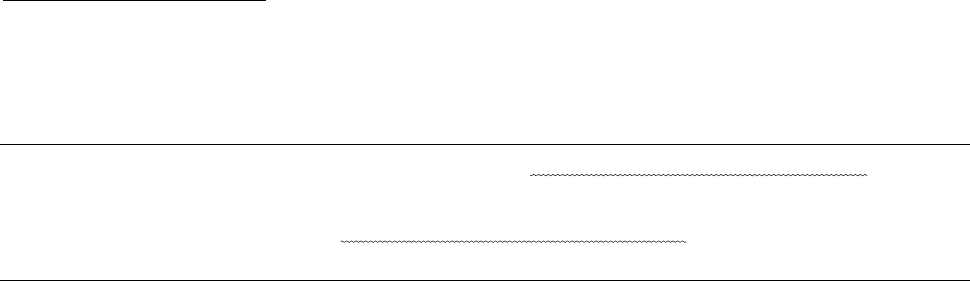
Рис. 2.11. Зависимость осмотического давления от температуры.
t
1
÷ t
2
– область дезагрегации.
2.5. Мембранное равновесие Доннана
Система представляет из себя сосуд, разделенный полупроницаемой
мембраной. По одну сторону (I) имеется раствор полиэлектролита c
концентрацией
c
1
.
NaR
R
–
+ Na
+
R
–
– ВМС, не проходит через мембрану.
По другую сторону (II) находится раствор низкомолекулярного
электролита концентрацией
c
2
(NaCl), который способен проходить через
мембрану.
Пусть
x – концентрация низкомолекулярного электролита перешедшего
по другую сторону мембраны:
Na
+
R
–
Cl
–
Na
+
Cl
–
I II
τ
c
1
c
1
0 c
2
c
2
0
c
1
+x c
1
x
c
2
-x c
2
-x
τ
Рис. 2.12. Схема перераспределения концентраций в сосуде при мембранном
равновесии со временем.
При равновесии, исходя из равенства химических потенциалов NaCl по
обе стороны мембраны, можем записать:
[Na
+
]
I
·[Cl
–
]
I
=[Na
+
]
II
·[Cl
–
]
II
(2.58)
(
c
1
+ x)⋅x = (c
2
– x)
2
(2.58a)
21
2
2
2cc
c
x
+
= (2.59)
Видим, что концентрация NaCl, перешедшего через мембрану x ≠ ½c
2
,
т. е. низкомолекулярный электролит распространяется по обе стороны
мембраны неодинаково.
x
xc
k
−
=
2
(2.60)

24
k – коэффициент распространения.
Подставив (2.59) в (2.60) получаем:
2
21
c
cc
k
+
= (2.60a)
Проанализируем:
а) c
1
<< c
2
; k = 1, x = ½ c
2
; низкомолекулярный электролит распределяется
поровну.
б) c
1
>> c
2
;
2
1
c
c
k = , x – мал.
Из-за разницы концентраций на мембрану действует осмотическое
давление:
π
изм
= π
1
– π
2
(2.61)
π
1
= 2с
1
RT + 2xRT (2.62)
π
2
= 2(с
2
– x)RT (2.63)
π
изм
= 2с
1
RT – 2(с
2
– 2x)RT (2.64)
(с
2
– 2x) выразим из (2.59):
21
21
21
2
2
2
221
21
2
2
22
22
22
2
22
cc
cc
cc
cccc
cc
c
cxc
+
=
+
−+
=
+
−=− (2.65)
(2.64) подставим в (2.63):
2
12 1 12 1 2
11
12 12 12
222
222
изм
cc c cc c c
RT c RT RTc
cc cc cc
⎛⎞
++
π= − = =
⎜⎟
+++
⎝⎠
(2.66)
Т. к. исходное осмотическое давление полиэлектролита π
NaR
= 2RTc
1
,
можем переписать выражение (2.66) в виде:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
π=π
21
21
2cc
cc
NaRизм
(2.67)
Проанализируем:
а) c
1
<< c
2
;
2
NaR
изм
π
=π
б) c
1
>> c
2
;
NaRизм
π=π
Таким образом измеряемое давление меняется от 0,5 π
NaR
до
π
NaR
= 2с
NaR
⋅RT
Это важно для биологических клеток, где концентрация
полиэлектролита ≈ 10% или 1 г-ион/л, вне клетки ≈ 1% = 0,1 г-ион/л
низкомолекулярного электролита. Т. е. c
1
> c
2
; полиэлектролит препятствует
проникновению низкомолекулярного электролита в клетку, поддерживает
стабильный солевой состав клетки при изменении его в окружающей среде.
Однако, в организме условия могут быть далеки от равновесных.
25
Допущения в расчете.
1)
pH и объемы растворов не изменялись,
2)
в I и II – один и тот же ион Na
+
.
Если концентрации ионов по обе стороны не равны, то возникает
мембранный потенциал.
0,9% раствор NaCl – изотонический раствор
, его
π = 7,7атм = π
плазмы крови
. Используют при обезвоживании организма, для
растворения лекарств. Гипертонический раствор
3–5–10% раствор,
применяется наружно в виде компрессов и примочки для лечения гнойных ран.
26
3. ОПТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ
3.1. Рассеяние света
При падении луча света на гетерогенные системы происходят следующие
оптические явления: дифракция и рассеяние света, если размер частиц ≤ 0,5 λ;
отражение света, если r
ч-ц
≥ λ.
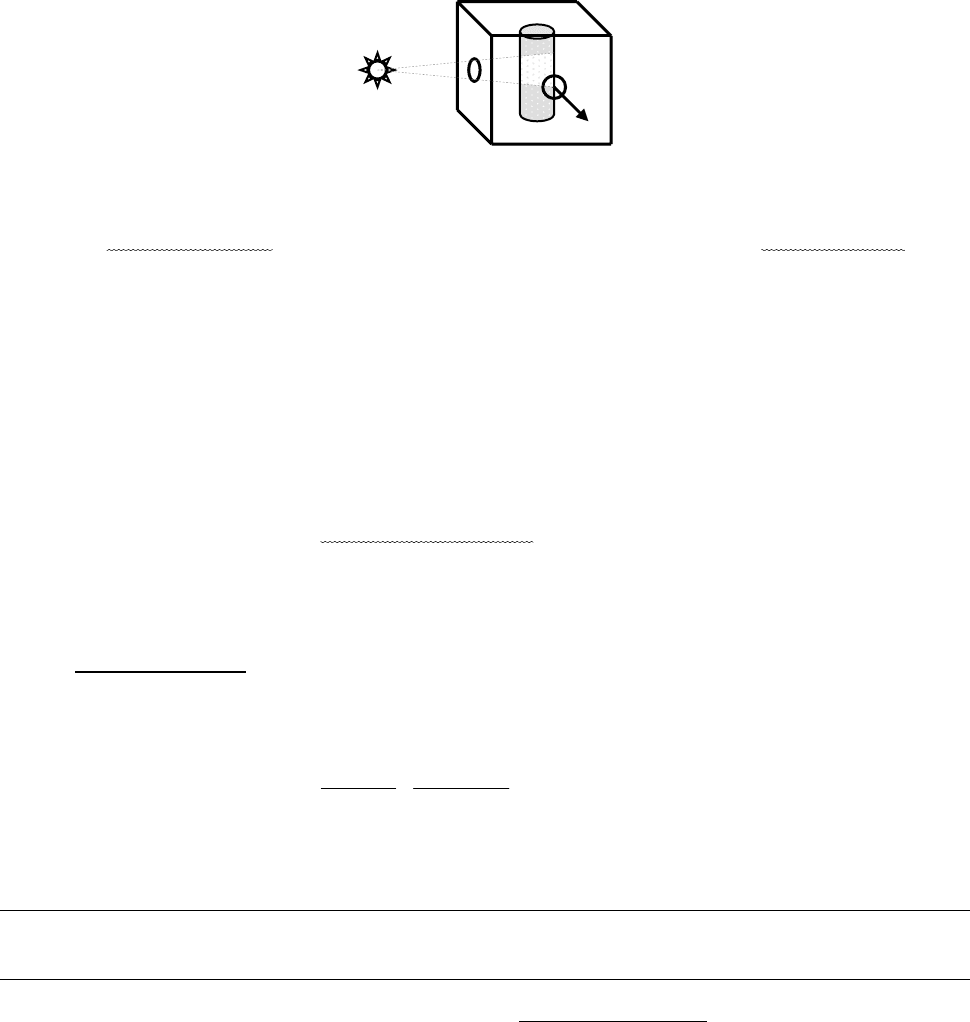
1857 г. Фарадей, 1868 г. Тиндаль наблюдали рассеяние света коллоидными
растворами – в виде светящегося конуса.
Рис. 3.1. Схема для наблюдения конуса Тиндаля.
При этом наблюдается окрашивание красноватым в проходящем свете,
голубой опалесцирует
в отраженном. Такое явление называют дихроизмом.
При прохождении электромагнитной волны через среду, в ней вследствие
поляризации возникает индуцированный дипольный момент, осциллирующий с
той же частотой, что и у световой волны. Осциллирующий диполь, в свою
очередь, также является источником электромагнитной волны. Если среда
сплошная, в результате интерференции остается только исходная световая
волна. Если же имеется дисперсная система,
т. е. есть фаза с отличной
поляризуемостью и, соответственно, показателем преломления (ε = n
2
), то будет
наблюдаться рассеяние света на частицах дисперсной фазы (так истинные
растворы не рассеивают – оптически пусты
).
Таким образом интенсивность рассеянного света должна зависеть от
показателей преломления дисперсной фазы и дисперсионной среды, размеров
частиц, их концентрации и длины волны падающего света.
1871 г. Рэлей
– в предположении, что размер частицы много меньше
длины волны падающего света (однородное электрическое поле внутри
частицы) получил выражение для общего потока рассеянного света от 1 см
3
:
2
32 2 2
0
р 0
422
0
24
2
Vnn
JJ
nn
⎛⎞
πν −
=
⎜⎟
λ+
⎝⎠
(3.1)
где ν – частичная концентрация [ч-ц/см
3
], V – объем одной частицы, n и n
0
–
показатели преломления дисперсной фазы и дисперсионной среды.
Имея уравнение (3.1), докажите, что интенсивность рассеянного света
есть функция (r
ч-цы
)
3
.
Рассеянный свет от 1 частицы имеет характеристики:
1.
интенсивность;
набл.
27
2.
распределение в пространстве;
3.
доля поляризованного излучения.
Для наблюдения под углом θ интенсивность поляризованного излучения:
2
22 22
2
0
,0
22 24
0
9
cos
2
р
nn V
JJ
nn R
θ
⎛⎞
−πν
=θ
⎜⎟
+λ
⎝⎠
(3.2)
R – расстояние до места наблюдения. Это уравнение – поверхность вращения
функции cos
2
θ вокруг оси θ = 0.
Суммарная интенсивность излучения:
()
2
22 22
2
0
0
22 24
0
9
1cos
22
nn V
JJ
nn R
⎛⎞
−πν
=+θ
⎜⎟
+λ
⎝⎠
(3.3)
Сечение этой поверхности называют диаграммой Ми
или индикатрисой
рассеяния неполяризованного падающего луча. В зависимости от размеров
частиц имеем в сечении виды:
а) r = 10
-7
÷10
-6
см
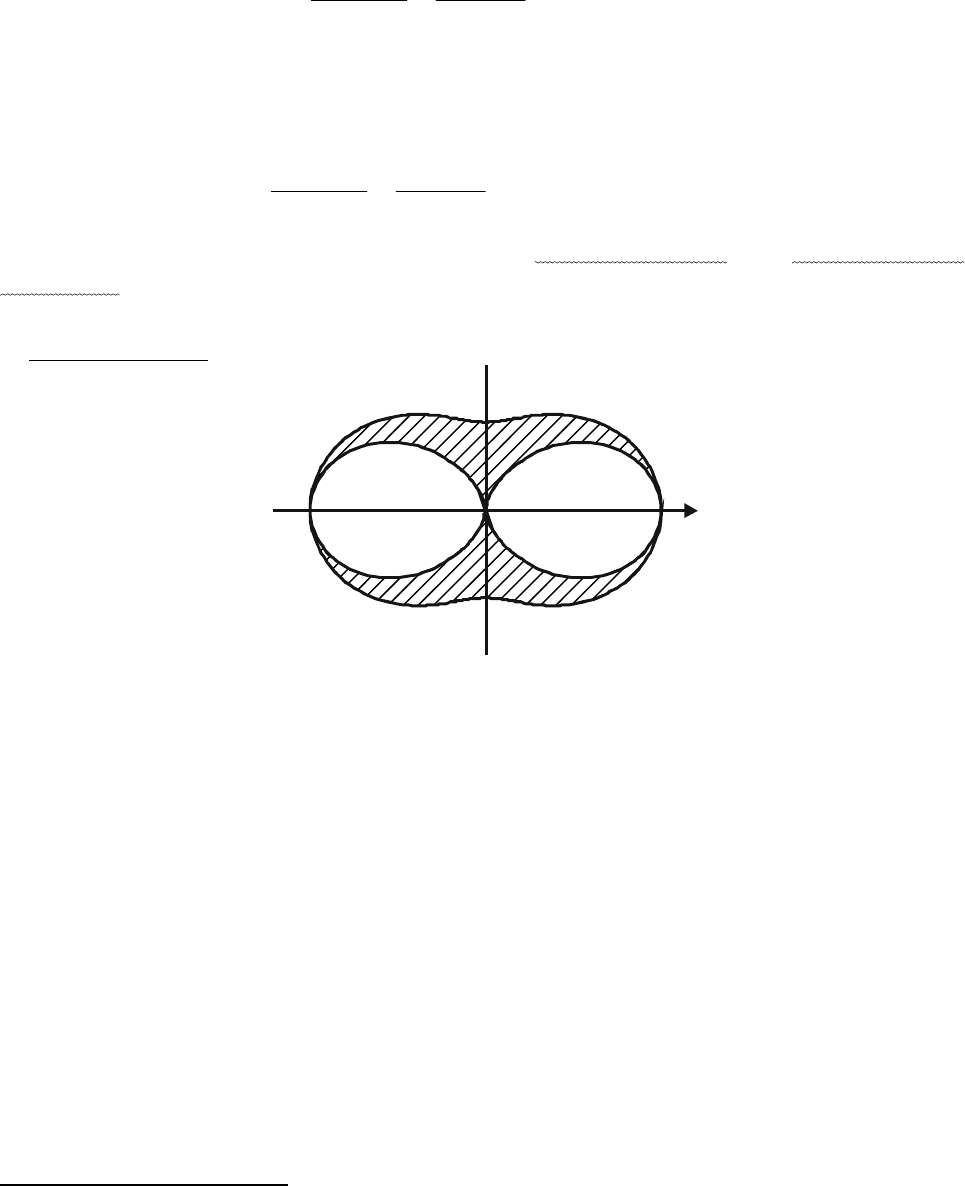
Рис. 3.2. Диаграмма рассеяния Ми для малой частицы (r << λ)
*
.
Стрелкой показано направление падающей световой волны. Внешняя
граница показывает суммарную интенсивность рассеянного света, внутренняя
незаштрихованная – доля неполяризованного света, соответственно
заштрихованная область – доля поляризованного (90° – максимум
поляризованного света 0° и 180° – неполяризованный свет).
Наблюдается симметричное распределение суммарной интенсивности в
пространстве: J
θ
= J
180-θ
.
*
Диаграммы (рис. 3.2 – 3.4) рассчитаны при помощи программы MiePlot © Philip Laven
(http://www.philiplaven.com/mieplot.htm).
28
б) r = 10
-5
см
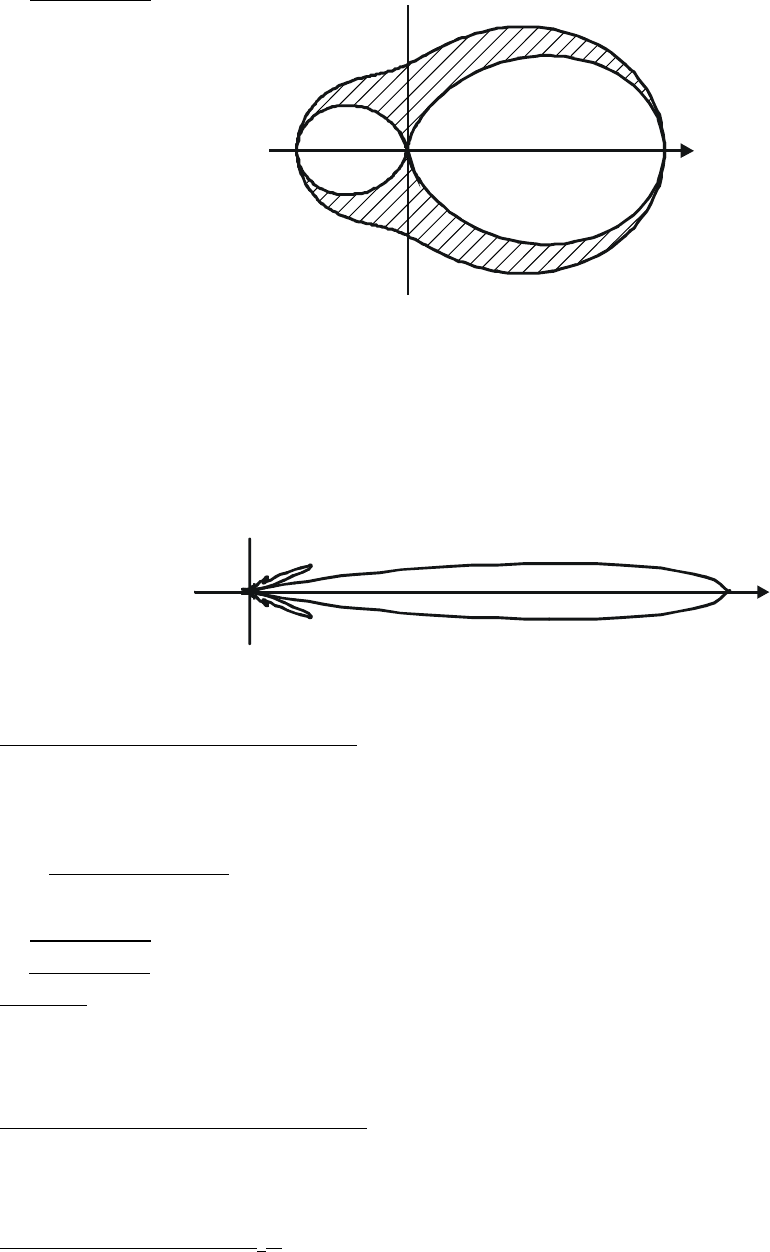
Рис. 3.3. Диаграмма рассеяния Ми для частицы с r = 10
-5
см.
Не описывается уравнением Рэлея, несимметричное распределение
интенсивности в пространстве: J
θ
≠ J
180-θ
.
При дальнейшем увеличении размеров частиц, форма диаграммы
усложняется, при этом сильно увеличивается доля рассеянного света в
направлении падающего луча, например ниже изображена суммарная
интенсивность рассеяния для частиц с r = 10
-4
см:
Рис. 3.4. Диаграмма рассеяния Ми для частицы радиусом r ≈ 2λ.
Зависимость от длины волны.
В уравнении Рэлея интенсивность рассеянного света обратно
пропорциональна длине волны падающего света в четвертой степени, но с
увеличением размеров частиц зависимость будет меняться:
а) r = 10
-6
÷10
-5
см (10 ÷ 100 нм) частицы рассеивают главным образом
фиолетовые и синие лучи (т. к. J
р.
~ λ
–4
);
б) r = 10
-4
см – все лучи рассеиваются одинаково;
в) r > 10
-4
см – отражение (мутность).
Вывод:
с увеличением размера частиц, исчезает зависимость интенсивности
рассеянного света от длины волны падающего излучения, J
р
= f(λ
-4
) → f(λ
0
)
Падающие лучи отражаются от частицы. Глаз человека видит мутный раствор.
Зависимость от концентрации.
С увеличением концентрации происходит многократное рассеяние,
необходимы поправки, поэтому уравнение Рэлея справедливо для C ≤ 1% вес.
Зависимость от (n – n
0
).
С увеличением разницы показателей преломления фазы и среды (n – n
0
),
интенсивность рассеянного света J
р
увеличивается и наоборот, например
глицерин + олеат натрия + CCl
4
⇒ нет рассеяния.

29
Зависимость от природы частиц.
Все сказанное выше справедливо для лиофобных золей с
диэлектрическими частицами:
Рис. 3.5. Зависимость интенсивности рассеяния
от размера частиц для золя BaSO
4
.
Для других диэлектриков зависимость интенсивности рассеяния от
размера частиц аналогичная.
Для металлов зависимость – сложная. У каждого металла свои
зависимости от длины волны и размеров частиц (рассматривается ниже).
Таким образом уравнение Рэлея можно использовать при условиях:
1.
золи неметаллов;
2.
сферическая частица;
3.
r ~ 0,1λ ≈ 10
-6
см;
4.
частицы оптически изотропны;
5.
концентрация ≤ 1% вес., когда расстояние между частицами >> λ;
6.
частицы не поглощают свет.
Рассеяние света и форма частиц
Рассмотрим рассеяние поляризованного света частицами сплющенной и
вытянутой формы. При ориентации частиц в растворе, существует три
возможных направления и два способа поляризации по каждому из
направлений:
r
1 мкм
J
р
0

30
Рис. 3.6. Схема для исследования рассеяния несферическими частицами.
J
1
– J
3
показывают возможные направления падающего луча;
E
а
, E
б
соответствуют двум возможным вариантам направления электрического
вектора световой волны перпендикулярно направлению падающего луча.
Условие рассеяния – электрический вектор падающего луча должен быть
параллелен длине палочкообразной или плоскости сплющенной частицы.
Тогда для шести возможных вариантов падения луча имеем:
1) 1а – 1б –
2) 2а – 2б –
3) 3а – 3б –
Итого:
– 4 раза светятся, – 2 раза светятся.
Таким образом, можно сделать вывод о форме находящихся в растворе
частиц.
3.2. Поглощение света золями
Дихроизм – было рассмотрено выше.
Полихромия
– изменение окраски с изменением размеров частиц.
Рассмотрим на примере золя золота. В зависимости от способа его получения,
золь имеет разную окраску:
1)
HAuCl
4
+ CH
3
COCH
3
→ Au-золь (синий)
2)
HAuCl
4
+ HCOH → Au-золь (вишневый)
3)
HAuCl
4
+ лимонная к-та → Au-золь (зеленый)
r
1
r
2
r
3
40-50 нм
>
20 нм
>
10 нм
λ
max погл
1
λ
2
λ
3
= 590 нм
>
530 нм
>
450 нм
(желтый) (зеленый) (синий)
J
2
J
3
J
1
E
а
E
б
E
а
E
б
E
а
E
б
