Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

вать как множество линии, конгруэнтных

профилю резца.

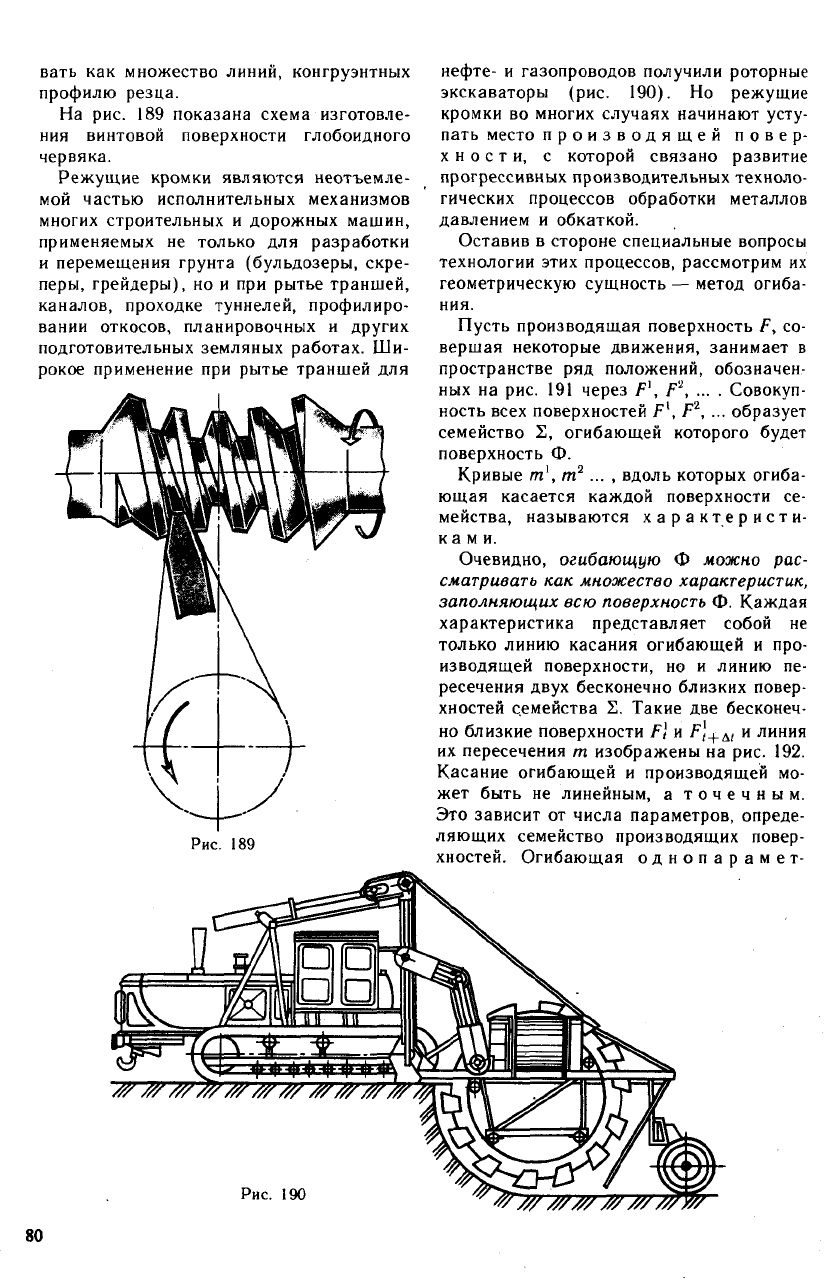
На рис. 189 показана схема изготовле-

ния винтовой поверхности глобоидного

червяка.

Режущие кромки являются неотъемле-

мой частью исполнительных механизмов

многих строительных и дорожных машин,

применяемых не только для разработки

и перемещения грунта (бульдозеры, скре-

перы, грейдеры), но и при рытье траншей,

каналов, проходке туннелей, профилиро-

вании откосов, планировочных и других

подготовительных земляных работах. Ши-

рокое применение при рытье траншей для

Рис. 189

нефте- и газопроводов получили роторные

экскаваторы (рис. 190). Но режущие

кромки во многих случаях начинают усту-

пать место производящей повер-

хности, с которой связано развитие

прогрессивных производительных техноло-

гических процессов обработки металлов

давлением и обкаткой.

Оставив в стороне специальные вопросы

технологии этих процессов, рассмотрим их

геометрическую сущность — метод огиба-

ния.

Пусть производящая поверхность F, со-

вершая некоторые движения, занимает в

пространстве ряд положений, обозначен-

ных на рис. 191 через F\ F... . Совокуп-

ность всех поверхностей F\ F'

, ... образует

семейство Е, огибающей которого будет

поверхность Ф.

Кривые т\ т

... , вдоль которых огиба-

ющая касается каждой поверхности се-

мейства, называются характеристи-

ками.

Очевидно, огибающую Ф можно рас-

сматривать как множество характеристик,

заполняющих всю поверхность Ф. Каждая

характеристика представляет собой не

только линию касания огибающей и про-

изводящей поверхности, но и линию пе-

ресечения двух бесконечно близких повер-

хностей семейства 2. Такие две бесконеч-

но близкие поверхности Fj и fJ+A, и линия

их пересечения m изображены на рис. 192.

Касание огибающей и производящей мо-

жет быть не линейным, а точечным.

Это зависит от числа параметров, опреде-

ляющих семейство производящих повер-

хностей. Огибающая однопарамет-

Рис. 190

/////////////////77//

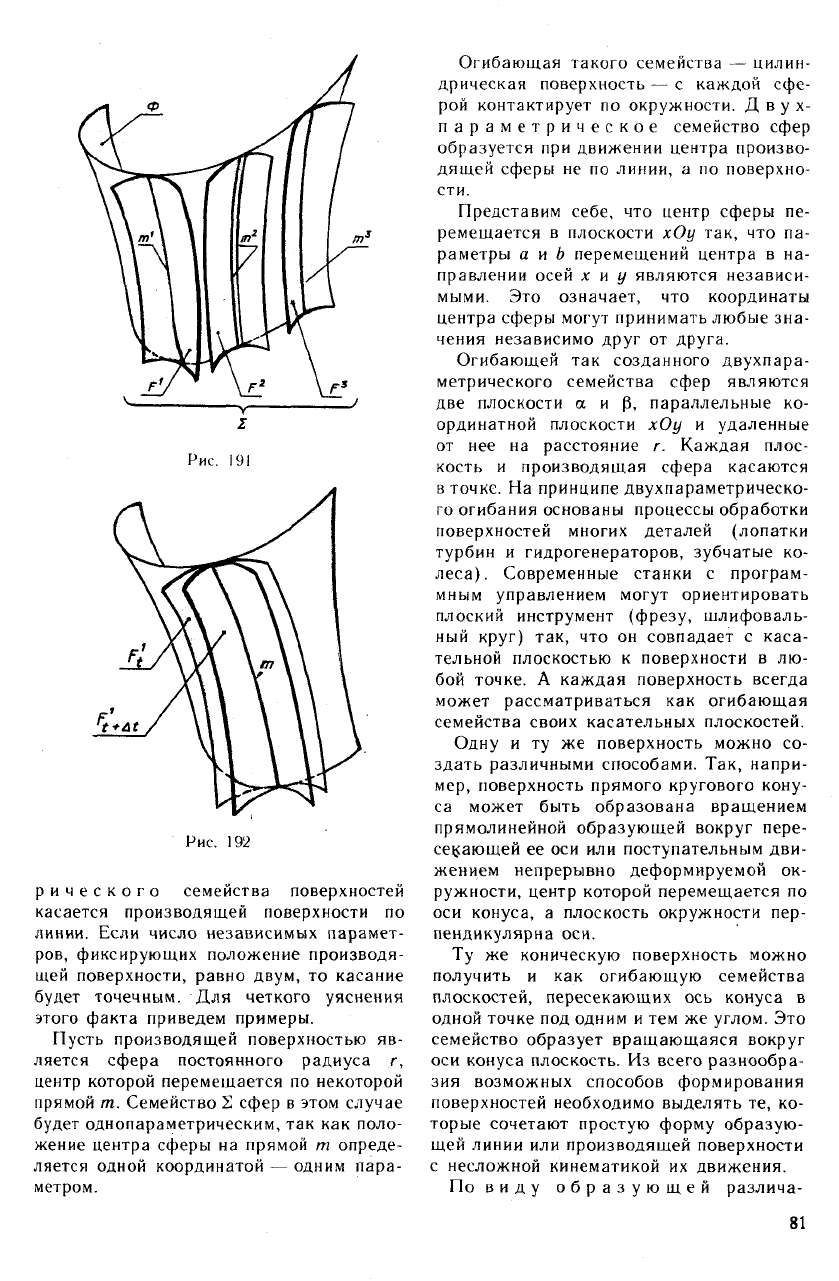
Рис. 191

Рис. 192

рического семейства поверхностей

касается производящей поверхности по

линии. Если число независимых парамет-

ров, фиксирующих положение производя-

щей поверхности, равно двум, то касание

будет точечным. Для четкого уяснения

этого факта приведем примеры.

Пусть производящей поверхностью яв-

ляется сфера постоянного радиуса г,

центр которой перемещается по некоторой

прямой т. Семейство 2 сфер в этом случае

будет однопараметрическим, так как поло-

жение центра сферы на прямой т опреде-

ляется одной координатой — одним пара-

метром.

Огибающая такого семейства — цилин-

дрическая поверхность — с каждой сфе-

рой контактирует по окружности. Д в у х-

параметрическое семейство сфер

образуется при движении центра произво-

дящей сферы не по линии, а по поверхно-

сти.

Представим себе, что центр сферы пе-

ремещается в плоскости хОу так, что па-

раметры а и b перемещений центра в на-

правлении осей х и у являются независи-

мыми. Это означает, что координаты

центра сферы могут принимать любые зна-

чения независимо друг от друга.

Огибающей так созданного двухпара-

метрического семейства сфер являются

две плоскости а и (3, параллельные ко-

ординатной плоскости хОу и удаленные

от нее на расстояние г. Каждая плос-

кость и производящая сфера касаются

в точке. На принципе двухпараметрическо-

го огибания основаны процессы обработки

поверхностей многих деталей (лопатки

турбин и гидрогенераторов, зубчатые ко-

леса). Современные станки с програм-

мным управлением могут ориентировать

плоский инструмент (фрезу, шлифоваль-

ный круг) так, что он совпадает с каса-

тельной плоскостью к поверхности в лю-

бой точке. А каждая поверхность всегда

может рассматриваться как огибающая

семейства своих касательных плоскостей.

Одну и ту же поверхность можно со-

здать различными способами. Так, напри-

мер, поверхность прямого кругового кону-

са может быть образована вращением

прямолинейной образующей вокруг пере-

секающей ее оси или поступательным дви-

жением непрерывно деформируемой ок-

ружности, центр которой перемещается по

оси конуса, а плоскость окружности пер-

пендикулярна оси.

Ту же коническую поверхность можно

получить и как огибающую семейства

плоскостей, пересекающих ось конуса в

одной точке под одним и тем же углом. Это

семейство образует вращающаяся вокруг

оси конуса плоскость. Из всего разнообра-

зия возможных способов формирования

поверхностей необходимо выделять те, ко-

торые сочетают простую форму образую-

щей линии или производящей поверхности

с несложной кинематикой их движения.

По виду образующей различа-

ют поверхности линейчатые и

нелинейчатые. Образующей первых

является прямая линия, а вторых — кри-

вая. Линейчатые поверхности разделяют

на так называемые развертывающиеся по-

верхности, которые можно без складок

и разрывов развернуть на плоскость, и не-

развертывающиеся.

Значительный класс поверхностей фор-

мируется движением окружности посто-

янного или переменного радиуса, Это так

называемые циклические поверхности.

Если же группировать поверхности по

закону движения образующей

линии и производящей повер-

хности, то большинство встречающихся

в технике поверхностей можно разделить

на: поверхности вращения;

винтовые поверхности; повер-

хности с плоскостью парал-

лелизма; поверхности перено-

с а.

Особое место занимают такие нелиней-

чатые поверхности, образование которых

не подчинено никакому кинематическому

закону. Оптимальную форму таких повер-

хностей определяют теми физическими ус-

ловиями, в которых они работают, и уста-

навливают ее (форму) эксперимен-

тально. Примером таких фасонных

поверхностей могут служить поверхности

лопастей турбин и нагнетателей, обшивки

каркасов морских судов, самолетов и авто-

мобилей. Эти поверхности изучают в спе-

циальных курсах в непосредственной свя-

зи с разработкой технологии их изготовле-

ния.

Ниже будут рассмотрены: поверхности

вращения, развертывающиеся, винтовые

поверхности, поверхности с плоскостью

параллелизма, циклические и поверхности

переноса.

При построении чертежей поверхностей

с помощью ЭВМ в условиях автоматизи-

рованных систем проектирования зачас-

тую требуются числовые характеристики,

определяющие положение точек и линий,

принадлежащих данной поверхности.

В ряде случаев это могут быть координаты

точек или векторов.

Ограничимся рассмотрением лишь одно-

го из возможных способов описания по-

верхности, позволяющего сравнительно

просто преобразовать геометрическую ин-

формацию о строении поверхности в циф-

ровую. Весьма удобной формой задания

поверхности является векторная, когда

радиус-вектор R. точки М поверхности

_(рис. 193) определяется вектор-функцией

R (и, у) двух скалярных независимых ар-

гументов и, v, рассматриваемых в некото-

рой области их изменения:

R=~R (u,v)=x (u,v)i+

+ у (u,v)] + z(u,v)~k, (8.1)

где х, у, z — координаты вектор-функции,

также являющиеся функциями и, v.

Заметим, что векторное равенство (8.1)

равносильно трем скалярным х = х (u,v),

у=у (и,v), z = z (u,v), которые являются

параметрическими уравнениями той же

поверхности. В дальнейшем будем пользо-

ваться и вектор-функцией, и ее координа-

тами.

Параметры и и у называются криволи-

нейными координатами поверхности. Каж-

дой паре значений и, v из области их

изменения соответствует точка поверхно-

сти. Если один из параметров принять

постоянным, например задаться v = ui, то

вектор-функция R = R (и, oi) представля-

ет одну из так называемых координатных

линий.

Иными словами, при фиксированном

^начении v и переменном и конец вектора

R = R (u,v\) опишет на поверхности ли-

нию

= const. Переходя к другому значе-

нию v = vn, получим следующую линию

семейства:

= const.

X /Ч/v

A/C /So*

чШ* J

»п \

X N.

Рис. 258

Множество линий, заполняющих повер-

хность

так, что

через каждую точку повер-

хности проходит в общем случае одна

линия этого множества, называется кар-

касом поверхности.

Аналогично, фиксируя и и изменяя и,

можно получить координатную линию и —

= const. Множество линий

= const (и =

Mi,

и=и

...) образует уже другой кар-

кас той же поверхности. Через каждую

точку поверхности можно провести две

координатные линии, которые и показаны

на рис. 193. Линии двух каркасов образу-

ют сеть, наглядной иллюстрацией которой

служат параллели и меридианы на повер-

хности глобуса. Здесь параметрами и и v

являются долгота и широта точки.

Познакомившись с основными способа-

ми образования поверхностей, поставим

перед собой следующие вопросы:

1. Как построить чертеж поверхности,

если известен закон ее образования или

она задана вектор-функцией R = R (u,v)?

2. Существуют ли универсальные мето-

ды решения позиционных задач на повер-

хности — методы, применение которых не

зависит от строения конкретной поверхно-

сти?

Ответы на эти вопросы содержатся в по-

следующих параграфах и связаны с важ-

ными понятиями каркаса и определителя

поверхности.

$ 41. ОПРЕДЕЛИТЕЛЬ

И КАРКАС ПОВЕРХНОСТИ

Для изображения поверхности необхо-

димо иметь данные, позволяющие постро-

ить ее непрерывный или дискретный кар-

кас.

Напомним, что каркасом называется

множество линий, заполняющих повер-

хность

так, что

через каждую точку повер-

хности в общем случае проходит одна

линия каркаса.

Поверхность может быть задана и ко-

нечным множеством точек, которое приня-

то называть точечным каркасом.

В этом случае поверхность в первом при-

ближении аппроксимируется поверхно-

стью многогранника, вписанного в дан-

ную поверхность. Вершины этого многог-

ранника расположены на поверхности,

гранями служат треугольники, образую-

щие триангуляционную сеть.

Рассмотренные в следующем параграфе

примеры покажут, что каркас поверхности

служит основой для создания универсаль-

ных методов решения всех позиционных

задач применительно к произвольной по-

верхности.

Трудами профессоров И. И. Котова,

Н. Н. Рыжова и их последователей созда-

на стройная логическая система, в которой

решение каждой последующей задачи

опирается на методику решения предыду-

щей.

Проекции каркаса могут быть построе-

ны, если задан определитель поверхно-

сти

— совокупность условий, задающих

поверхность в пространстве и на чертеже.

Различают две части определителя — ге-

ометрическую и алгоритми-

ческую.

Геометрическая часть определителя

представляет собой набор постоянных гео-

метрических элементов (точек, прямых,

плоскостей и т.п.), которые могут и не

входить в состав поверхности.

Вторая часть — алгоритмическая (опи-

сательная) — содержит перечень опера-

ций, позволяющих реализовать переход от

фигуры постоянных элементов к непрерыв-

ному каркасу.

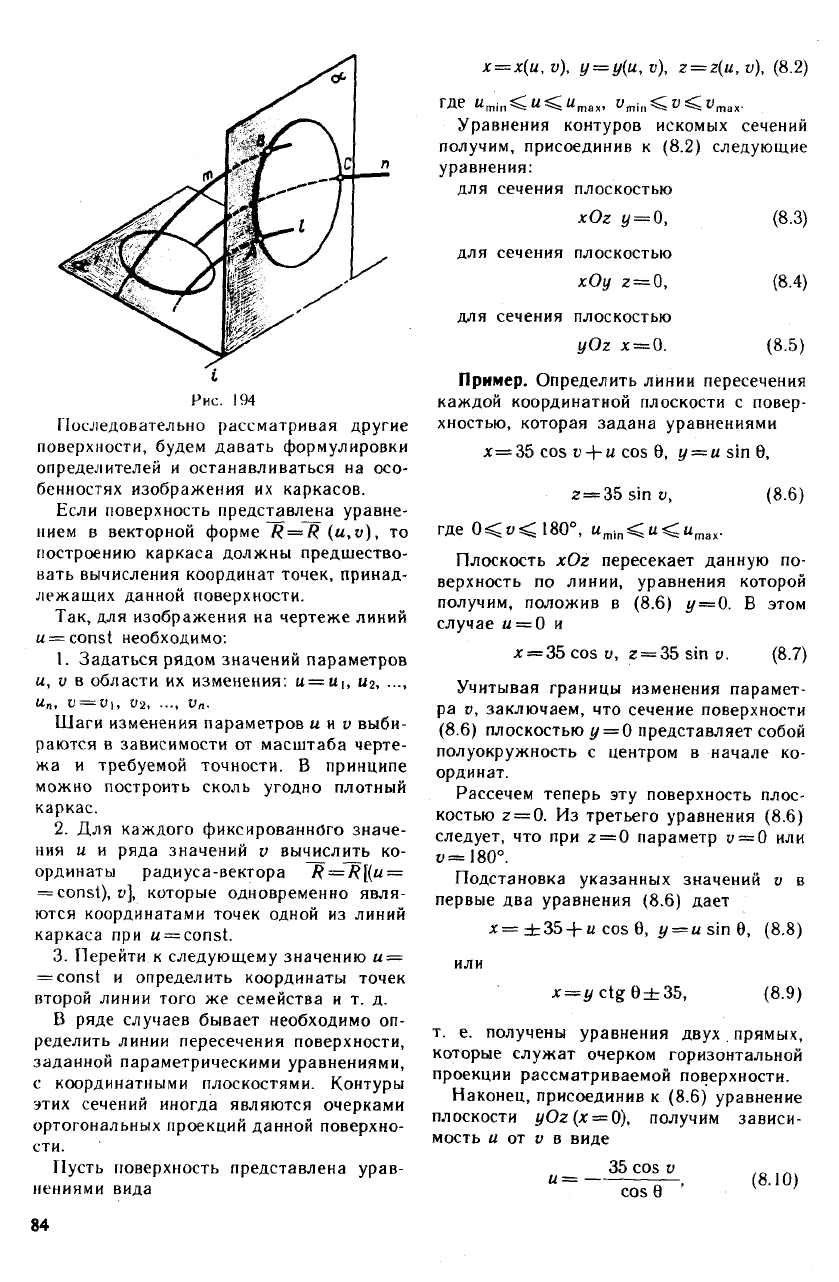
Так, например, циклическая повер-

хность *, каркас которой состоит из ок-

ружностей, может быть Задана следую-

щим образом (рис. 194).

Геометрическая часть определи-

теля:

три направляющие I, т, п;

ось i пучка плоскостей.

Алгоритмическая часть:

выделяем из пучка плоскостей с осью

i одну — плоскость а; находим точки А, В,

С, в которых а пересекает соответственно

направляющие /, т, и;

строим окружность, определяемую тре-

мя найденными точками;

переходим к следующей плоскости

а' того же пучка и повторяем построения,

описанные выше.

* Циклическая поверхность образуется при

движении окружности постоянного или пере-

менного радиуса. Этой поверхности посвящен

$ 46.

x—x(u, v), у = у(и, v), z = z(u, v), (8.2)

Рис. 194

Последовательно рассматривая другие

поверхности, будем давать формулировки

определителей и останавливаться на осо-

бенностях изображения их каркасов.

Если поверхность представлена уравне-

нием в векторной форме R = R (u,v), то

построению каркаса должны предшество-

вать вычисления координат точек, принад-

лежащих данной поверхности.

Так, для изображения на чертеже линий

u = const необходимо:

1. Задаться рядом значений параметров

и, v в области их изменения:

= tti, ы

, ••-,

= VU У

VN•

Шаги изменения параметров и и у выби-

раются в зависимости от масштаба черте-

жа и требуемой точности. В принципе

можно построить сколь угодно плотный

каркас.

2. Для каждого фиксированного значе-

ния и и ряда значений v вычислить ко-

ординаты радиуса-вектора R = R[(u —

= const), и], которые одновременно явля-

ются координатами точек одной из линий

каркаса при

= const.

3. Перейти, к следующему значению и —

= const и определить координаты точек

второй линии того же семейства и т. д.

В ряде случаев бывает необходимо оп-

ределить линии пересечения поверхности,

заданной параметрическими уравнениями,

с координатными плоскостями. Контуры

этих сечений иногда являются очерками

ортогональных проекций данной поверхно-

сти.

Пусть поверхность представлена урав-

нениями вида

где и

т1п

<ы<к

та

„

Уравнения контуров искомых сечений

получим, присоединив к (8.2) следующие

уравнения:

для сечения плоскостью

xOz у = О,

для сечения плоскостью

хОу 2 = 0,

для сечения плоскостью

yOz jc = 0.

(8.3)

(8.4)

(8.5)

Пример. Определить линии пересечения

каждой координатной плоскости с повер-

хностью, которая задана уравнениями

х=35 cos v -\-и cos 9, у—

sin 8,

2 = 35 sin v, (8.6)

где 0<у<180°, u

mln

<и<«„,„.

Плоскость xOz пересекает данную по-

верхность по линии, уравнения которой

получим, положив в (8.6) у —

О.

В этом

случае и = 0 и

л: = 35 cos v, z = 35 sin v. (8.7)

Учитывая границы изменения парамет-

ра v, заключаем, что сечение поверхности

(8.6) плоскостью у — 0 представляет собой

полуокружность с центром в начале ко-

ординат.

Рассечем теперь эту поверхность плос-

костью z = 0. Из третьего уравнения (8.6)

следует, что при 2 = 0 параметр у = 0 или

v =180°.

Подстановка указанных значений v в

первые два уравнения (8.6) дает

*= ±35+и cos в, у =

sin 9, (8.8)

или

х=у ctg 9±35,

(8.9)

т. е. получены уравнения двух. прямых,

которые служат очерком горизонтальной

проекции рассматриваемой поверхности.

Наконец, присоединив к (8.6) уравнение

плоскости y0z(x = 0), получим зависи-

мость и от у в виде

и =

35 cos v

cos в '

(8.10)

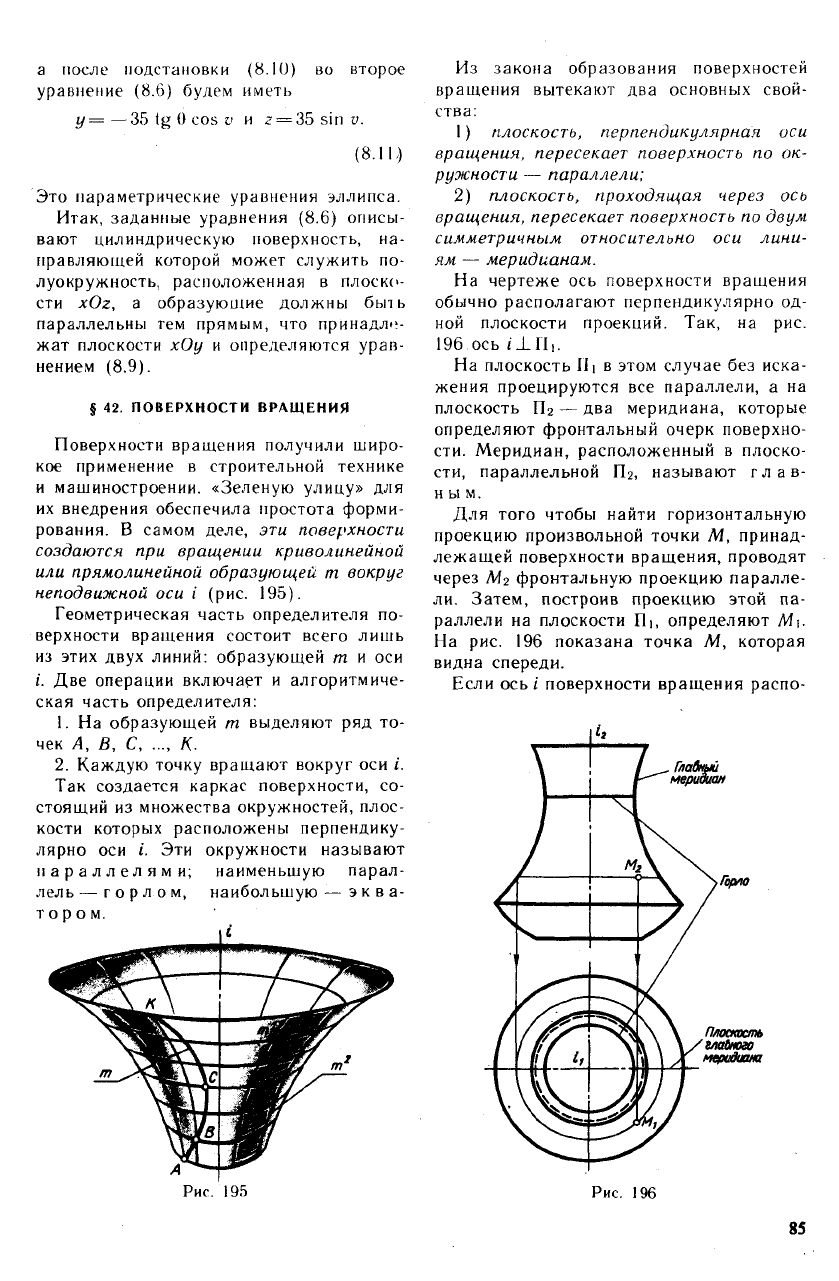
а после подстановки (8.10) во второе

уравнение (8.6) будем иметь

у=

— 35

tg 0 cos v и г =

sin У.

(8.11,)

Это параметрические уравнения эллипса.

Итак, заданные уравнения (8.6) описы-

вают цилиндрическую поверхность, на-

правляющей которой может служить по-

луокружность, расположенная в плоско-

сти xOz, а образующие должны бьпь

параллельны тем прямым, что принадле-

жат плоскости хОу и определяются урав-

нением (8.9).

§ 42. ПОВЕРХНОСТИ ВРАЩЕНИЯ

Поверхности вращения получили широ-

кое применение в строительной технике

и машиностроении. «Зеленую улицу» для

их внедрения обеспечила простота форми-

рования. В самом деле, эти поверхности

создаются при вращении криволинейной

или прямолинейной образующей m вокруг

неподвижной оси i (рис. 195).

Геометрическая часть определителя по-

верхности вращения состоит всего лишь

из этих двух линий: образующей m и оси

i. Две операции включает и алгоритмиче-

ская часть определителя:

1. На образующей m выделяют ряд то-

чек А, В, С, ..., К.

2. Каждую точку вращают вокруг оси г.

Так создается каркас поверхности, со-

стоящий из множества окружностей, плос-

кости которых расположены перпендику-

лярно оси г. Эти окружности называют

параллелями; наименьшую парал-

лель— горлом, наибольшую — эква-

тором.

Рис. 195

Из закона образования поверхностей

вращения вытекают два основных свой-

ства:

1) плоскость, перпендикулярная оси

вращения, пересекает поверхность по ок-

ружности — параллели;

2) плоскость, проходящая через ось

вращения, пересекает поверхность по двум

симметричным относительно оси лини-

ям — меридианам.

На чертеже ось поверхности вращения

обычно располагают перпендикулярно од-

ной плоскости проекций. Так, на рис.

196 ось /±11,.

На плоскость Hi в этом случае без иска-

жения проецируются все параллели, а на

плоскость Пг — два меридиана, которые

определяют фронтальный очерк поверхно-

сти. Меридиан, расположенный в плоско-

сти, параллельной Пг, называют глав-

ным.

Для того чтобы найти горизонтальную

проекцию произвольной точки М, принад-

лежащей поверхности вращения, проводят

через М

фронтальную проекцию паралле-

ли. Затем, построив проекцию этой па-

раллели на плоскости Пь определяют Ми

На рис. 196 показана точка М, которая

видна спереди.

Если ось г поверхности вращения распо-

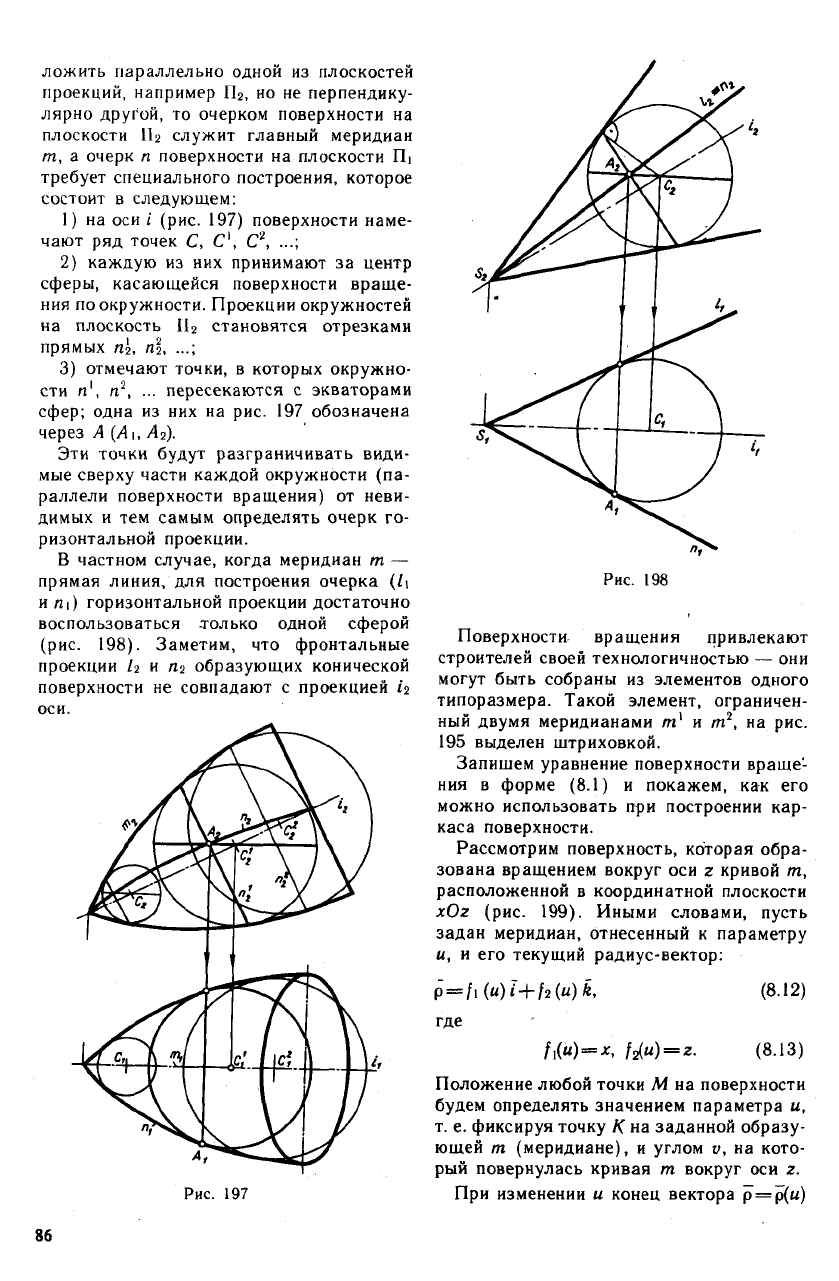
ложить параллельно одной из плоскостей

проекций, например П

, но не перпендику-

лярно другой, то очерком поверхности на

плоскости 1Ь служит главный меридиан

т, а очерк п поверхности на плоскости П]

требует специального построения, которое

состоит в следующем:

1) на оси i (рис. 197) поверхности наме-

чают ряд точек С, С\ С

, ...;

2) каждую из них принимают за центр

сферы, касающейся поверхности враще-

ния по окружности. Проекции окружностей

на плоскость 11

становятся отрезками

прямых n

, "г, ...;

3) отмечают точки, в которых окружно-

сти ft

, ft

, ... пересекаются с экваторами

сфер; одна из них на рис. 197 обозначена

через Л (Л,, Л

Эти точки будут разграничивать види-

мые сверху части каждой окружности (па-

раллели поверхности вращения) от неви-

димых и тем самым определять очерк го-

ризонтальной проекции.

В частном случае, когда меридиан т —

прямая линия, для построения очерка (/i

и ni) горизонтальной проекции достаточно

воспользоваться .только одной сферой

(рис. 198). Заметим, что фронтальные

проекции /

и п

образующих конической

поверхности не совпадают с проекцией i

Поверхности вращения привлекают

строителей своей технологичностью — они

могут быть собраны из элементов одного

типоразмера. Такой элемент, ограничен-

ный двумя меридианами от

и т

, на рис.

195 выделен штриховкой.

Запишем уравнение поверхности враще-

ния в форме (8.1) и покажем, как его

можно использовать при построении кар-

каса поверхности.

Рассмотрим поверхность, которая обра-

зована вращением вокруг оси z кривой т,

расположенной в координатной плоскости

хОг (рис. 199). Иными словами, пусть

задан меридиан, отнесенный к параметру

и, и его текущий радиус-вектор:

р = /,(ф

+Ы")*. (8.12)

где

/,(«)-*. Ш = г. (8.13)

Положение любой точки М на поверхности

будем определять значением параметра и,

т. е. фиксируя точку К на заданной образу-

ющей т (меридиане), и углом v, на кото-

рый повернулась кривая т вокруг оси г.

При изменении и конец вектора р = р(и)

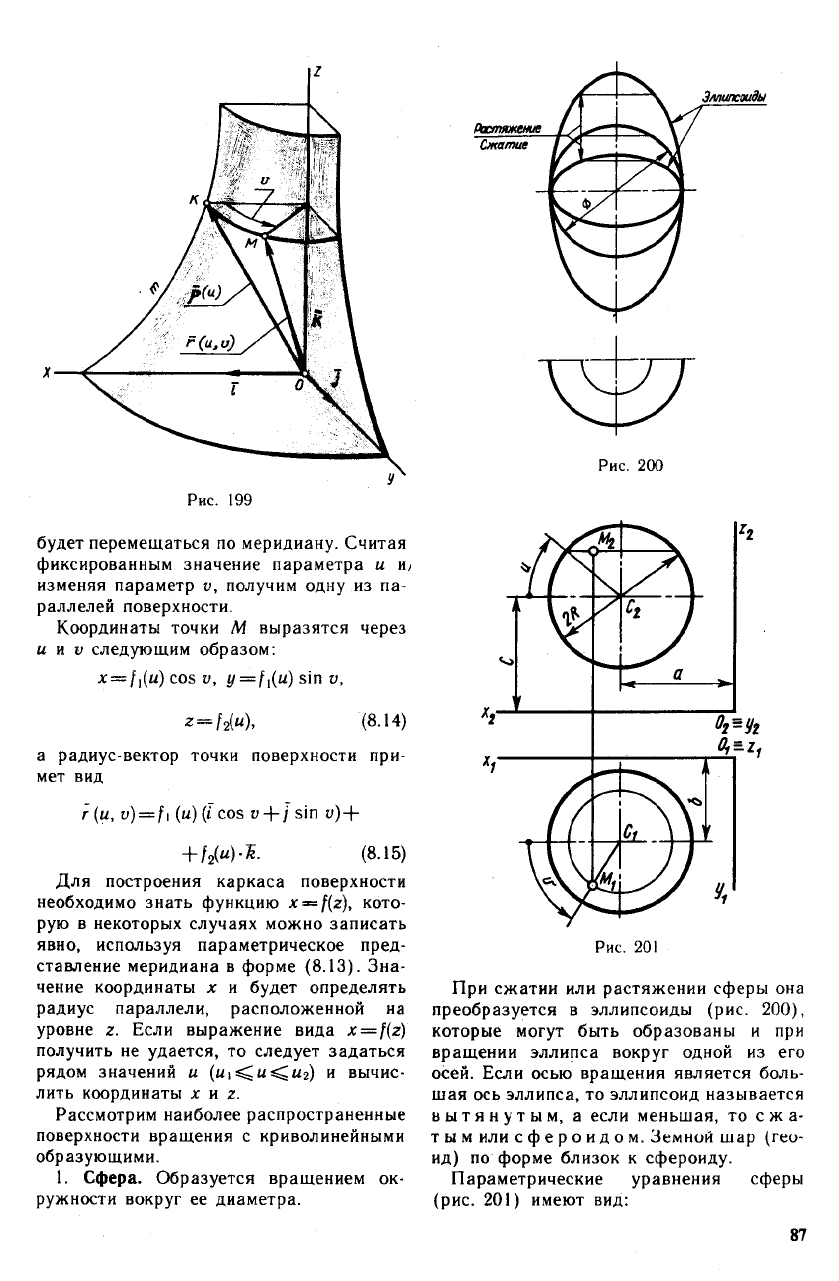
будет перемещаться по меридиану. Считая

фиксированным значение параметра и и,

изменяя параметр v, получим одну из па-

раллелей поверхности.

Координаты точки М выразятся через

и и v следующим образом:

—

f|(ы)

cos v, y=f

(u) sin V,

г = (8-14)

а радиус-вектор точки поверхности при-

мет вид

г (u, v) — f

(u){i cos v + j sin +

+ f

(u)-£. (8.15)

Для построения каркаса поверхности

необходимо знать функцию x = f(z), кото-

рую в некоторых случаях можно записать

явно, используя параметрическое пред-

ставление меридиана в форме (8.13). Зна-

чение координаты х и будет определять

радиус параллели, расположенной на

уровне 2. Если выражение вида x = f(z)

получить не удается, то следует задаться

рядом значений и (MI<U^M2) И вычис-

лить координаты х и г.

Рассмотрим наиболее распространенные

поверхности вращения с криволинейными

образующими.

1. Сфера. Образуется вращением ок-

ружности вокруг ее диаметра.

При сжатии или растяжении сферы она

преобразуется в эллипсоиды (рис. 200),

которые могут быть образованы и при

вращении эллипса вокруг одной из его

осей. Если осью вращения является боль-

шая ось эллипса, то эллипсоид называется

вытянутым, а если меньшая, то сжа-

тым или сфероидом. Земной шар (гео-

ид) по форме близок к сфероиду.

Параметрические уравнения сферы

(рис. 201) имеют вид:

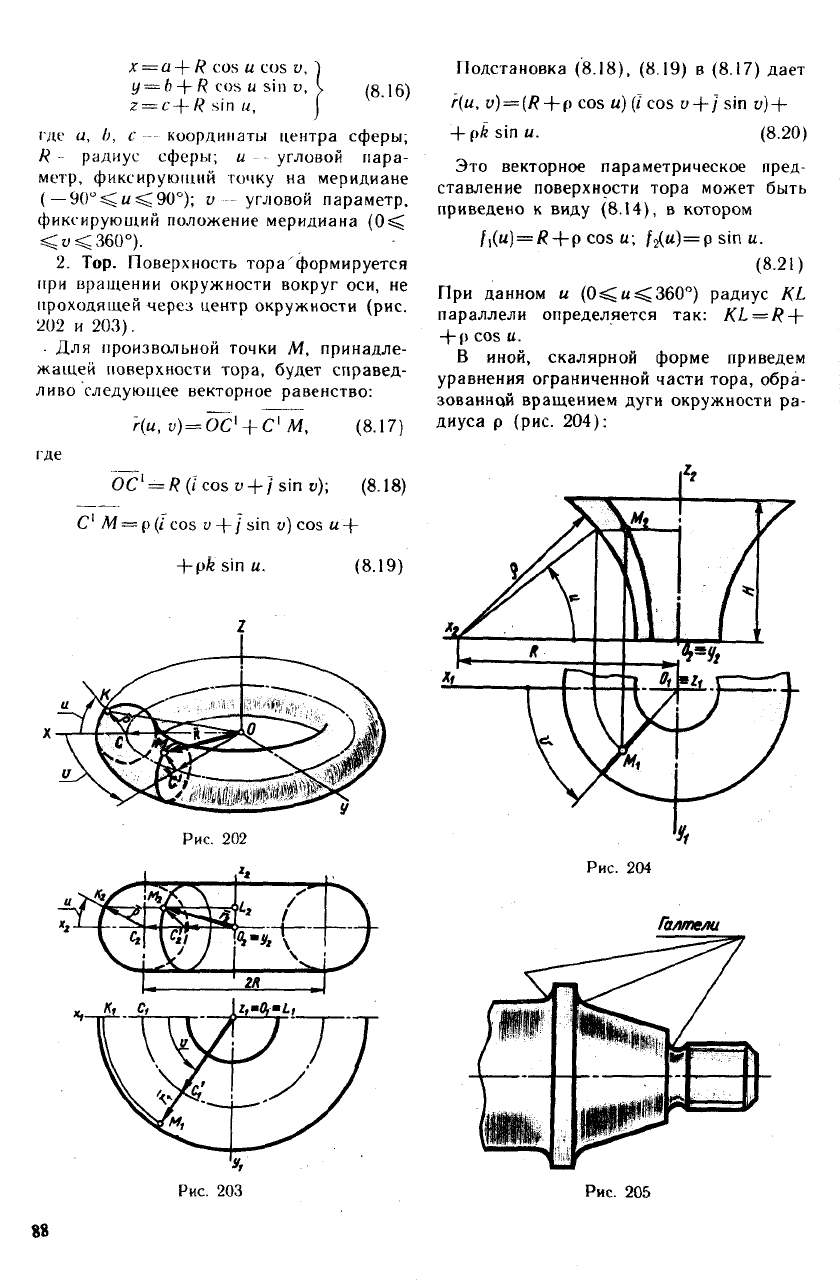
х = а + R cos и cos и, "1

y — b-'rR cos u sin v, ч (816)

= C-\-R sin u, j

где и, l>, с координаты центра сферы;

R радиус сферы; «--угловой пара-

метр, фиксирующий точку на меридиане

( — 90° ^ыг^ 90°); v -- угловой параметр,

фиксирующий положение меридиана (0^

<у<360°).

2. Тор. Поверхность тора формируется

при вращении окружности вокруг оси, не

проходящей через центр окружности (рис.

202 и 203).

• Для произвольной точки М, принадле-

жащей поверхности тора, будет справед-

ливо следующее векторное равенство:

r(u,v) = OC

+ C

M, (8.17)

где

ОС

= R(i cos v + ] sin к); (8.18)

—

()(i cos

+ / sin v) cos

и -f-

-fpfcsin u. (8.19)

Подстановка (8.18), (8.19) в (8.17) дает

r(u, u) = (/?-|-p cos и) (i cos v + / sin u) +

(>k

sin u. (8.20)

Это векторное параметрическое пред-

ставление поверхности тора может быть

приведено к виду (8.14), в котором

]

(u) = R-\-р cos и\

f<£u)

= p sin и.

(8.21)

При данном и (0^«<360°) радиус KL

параллели определяется так: KL=R-j-

+ р cos и.

В иной, скалярной форме приведем

уравнения ограниченной части тора, обра-

зованной вращением дуги окружности ра-

диуса р (рис. 204):

Галтели

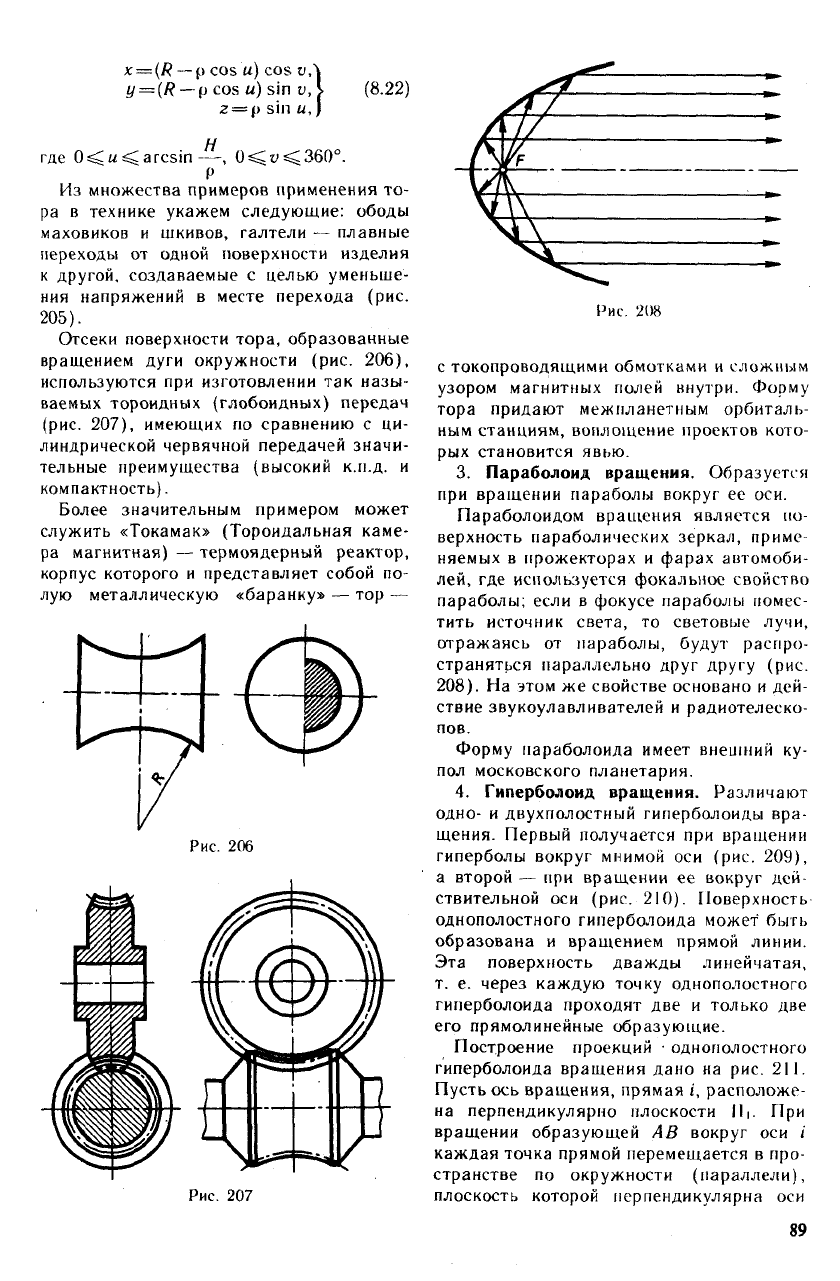
x — (R

—

P cos M) COS U,]

y = (R

— p

cos

z--

is u) cos и Л

os и) sin v, I

z = p sin u,)

(8.22)

Рис. 206

где 0<w<arcsin—, 0<y<360°.

Из множества примеров применения то-

ра в технике укажем следующие: ободы

маховиков и шкивов, галтели — плавные

переходы от одной поверхности изделия

к другой, создаваемые с целью уменьше-

ния напряжений в месте перехода (рис.

205).

Отсеки поверхности тора, образованные

вращением дуги окружности (рис. 206),

используются при изготовлении так назы-

ваемых тороидных (глобоидных) передач

(рис. 207), имеющих по сравнению с ци-

линдрической червячной передачей значи-

тельные преимущества (высокий к.п.д. и

компактность).

Более значительным примером может

служить «Токамак» (Тороидальная каме-

ра магнитная) — термоядерный реактор,

корпус которого и представляет собой по-

лую металлическую «баранку» — тор —

Рис.

258

Рис. 208

с токопроводящими обмотками и сложным

узором магнитных полей внутри. Форму

тора придают межпланетным орбиталь-

ным станциям, воплощение проектов кото-

рых становится явью.

3. Параболоид вращения. Образуется

при вращении параболы вокруг ее оси.

Параболоидом вращения является по-

верхность параболических зеркал, приме-

няемых в прожекторах и фарах автомоби-

лей, где используется фокальное свойство

параболы; если в фокусе параболы помес-

тить источник света, то световые лучи,

отражаясь от параболы, будут распро-

страняться параллельно друг другу (рис.

208). На этом же свойстве основано и дей-

ствие звукоулавливателей и радиотелеско-

пов.

Форму параболоида имеет внешний ку-

пол московского планетария.

4. Гиперболоид вращения. Различают

одно- и двухполостный гиперболоиды вра-

щения. Первый получается при вращении

гиперболы вокруг мнимой оси (рис. 209),

а второй — при вращении ее вокруг дей-

ствительной оси (рис. 210). Поверхность

однополостного гиперболоида может' быть

образована и вращением прямой линии.

Эта поверхность дважды линейчатая,

т. е. через каждую точку однополостного

гиперболоида проходят две и только две

его прямолинейные образующие.

Построение проекций

•

однополостного

гиперболоида вращения дано на рис. 211.

Пусть ось вращения, прямая г, расположе-

на перпендикулярно плоскости П|. При

вращении образующей АВ вокруг оси i

каждая точка прямой перемещается в про-

странстве по окружности (параллели),

плоскость которой перпендикулярна оси