Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

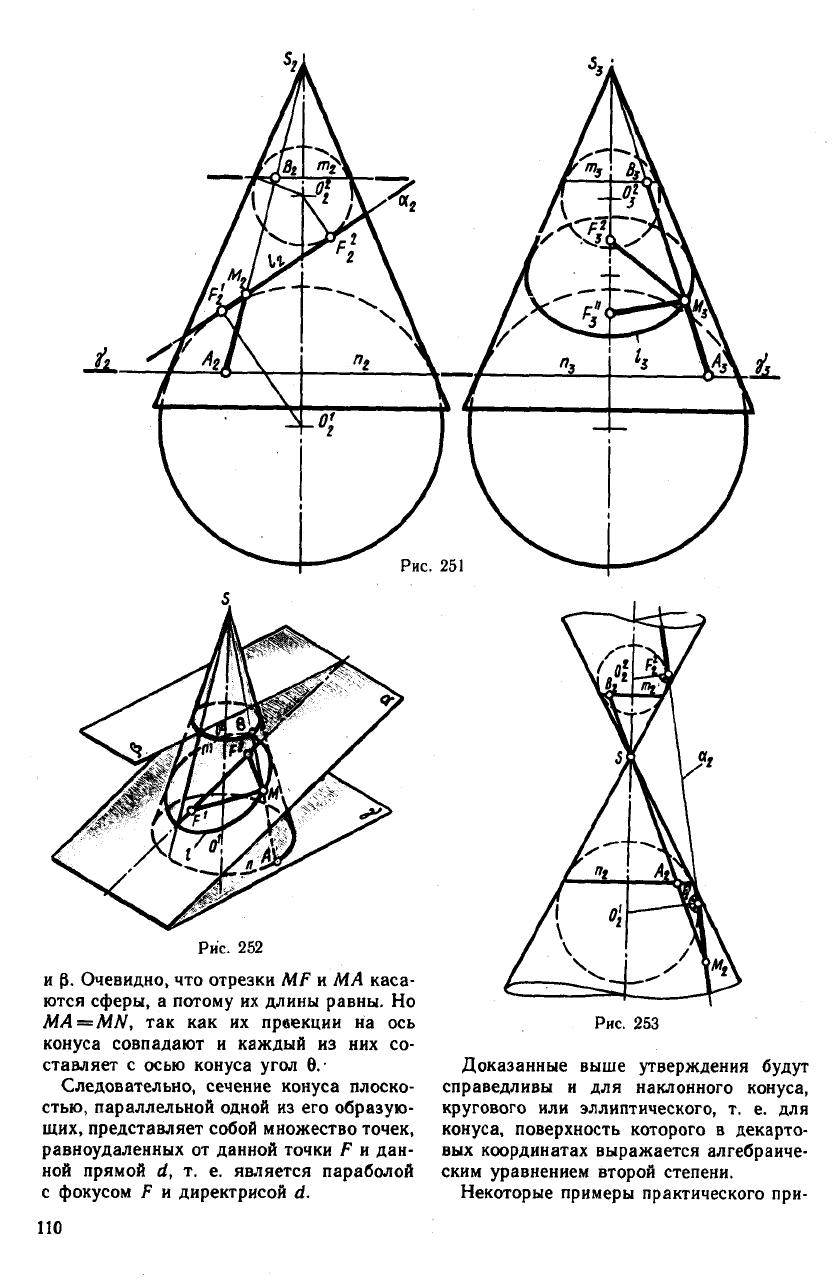
Рис. 252

и р. Очевидно, что отрезки MF и МА каса-

ются сферы, а потому их длины равны. Но

MA=MN, так как их првекции на ось

конуса совпадают и каждый из них со-

ставляет с осью конуса угол 9.

Следовательно, сечение конуса плоско-

стью, параллельной одной из его образую-

щих, представляет собой множество точек,

равноудаленных от данной точки F и дан-

ной прямой d, т. е. является параболой

с фокусом F и директрисой d.

Доказанные выше утверждения будут

справедливы и для наклонного конуса,

кругового или эллиптического, т. е. для

конуса, поверхность которого в декарто-

вых координатах выражается алгебраиче-

ским уравнением второй степени.

Некоторые примеры практического при-

110

менения поверхностей, образующими ко-

торых являются конические сечения, были

приведены в § 42. Построение ортогональ-

ных проекций одного из конических сече-

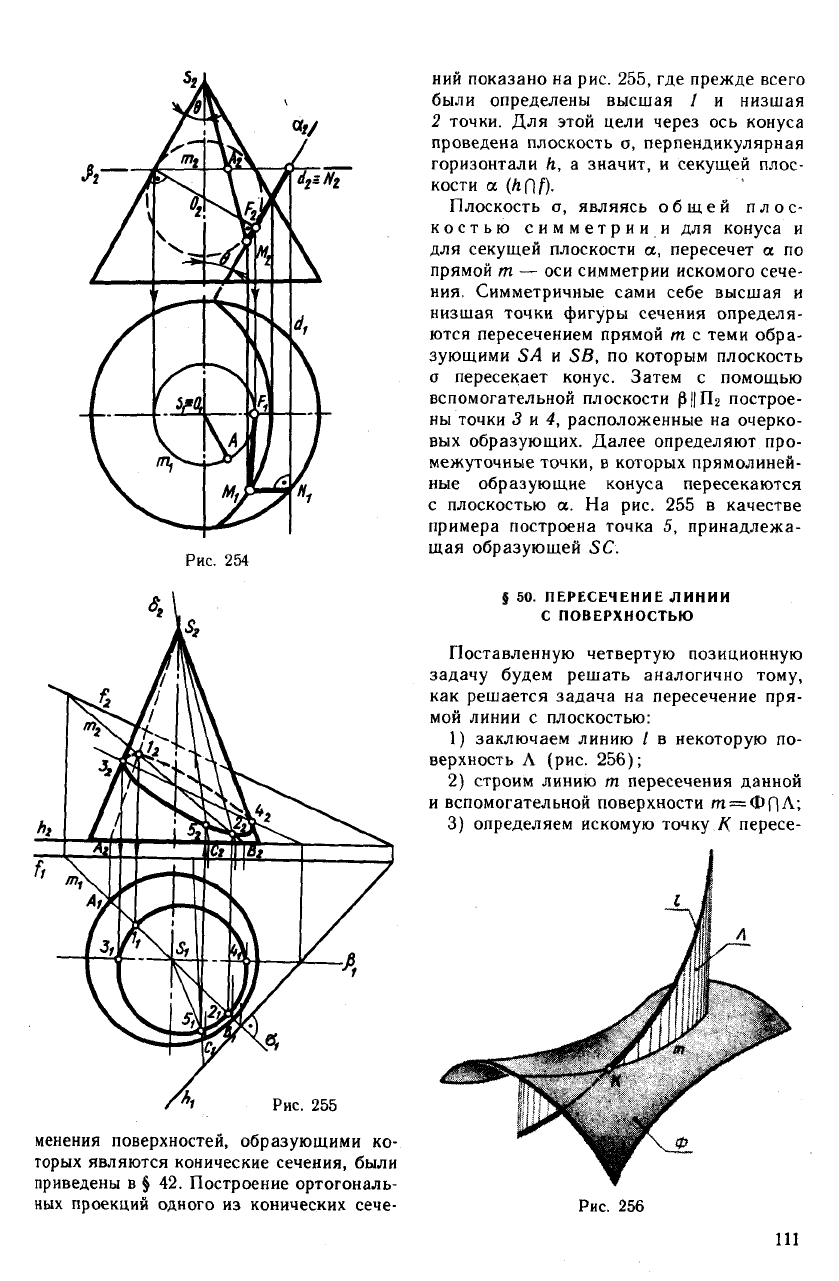
ний показано на рис. 255, где прежде всего

были определены высшая / и низшая

2 точки. Для этой цели через ось конуса

проведена плоскость о, перпендикулярная

горизонтали h, а значит, и секущей плос-

кости а (ЛИ/)-

Плоскость а, являясь общей плос-

костью симметрии.и для конуса и

для секущей плоскости а, пересечет а по

прямой т — оси симметрии искомого сече-

ния. Симметричные сами себе высшая и

низшая точки фигуры сечения определя-

ются пересечением прямой т с теми обра-

зующими S/4 и SB, по которым плоскость

а пересекает конус. Затем с помощью

вспомогательной плоскости р

Пг построе-

ны точки 3 н 4, расположенные на очерко-

вых образующих. Далее определяют про-

межуточные точки, в которых прямолиней-

ные образующие конуса пересекаются

с плоскостью а. На рис. 255 в качестве

примера построена точка 5, принадлежа-

щая образующей SC.

§ 50. ПЕРЕСЕЧЕНИЕ ЛИНИИ

С ПОВЕРХНОСТЬЮ

Поставленную четвертую позиционную

задачу будем решать аналогично тому,

как решается задача на пересечение пря-

мой линии с плоскостью:

1) заключаем линию / в некоторую по-

верхность Л (рис. 256);

2) строим линию т пересечения данной

и вспомогательной поверхности т = Ф("|Л;

3) определяем искомую точку К пересе-

111

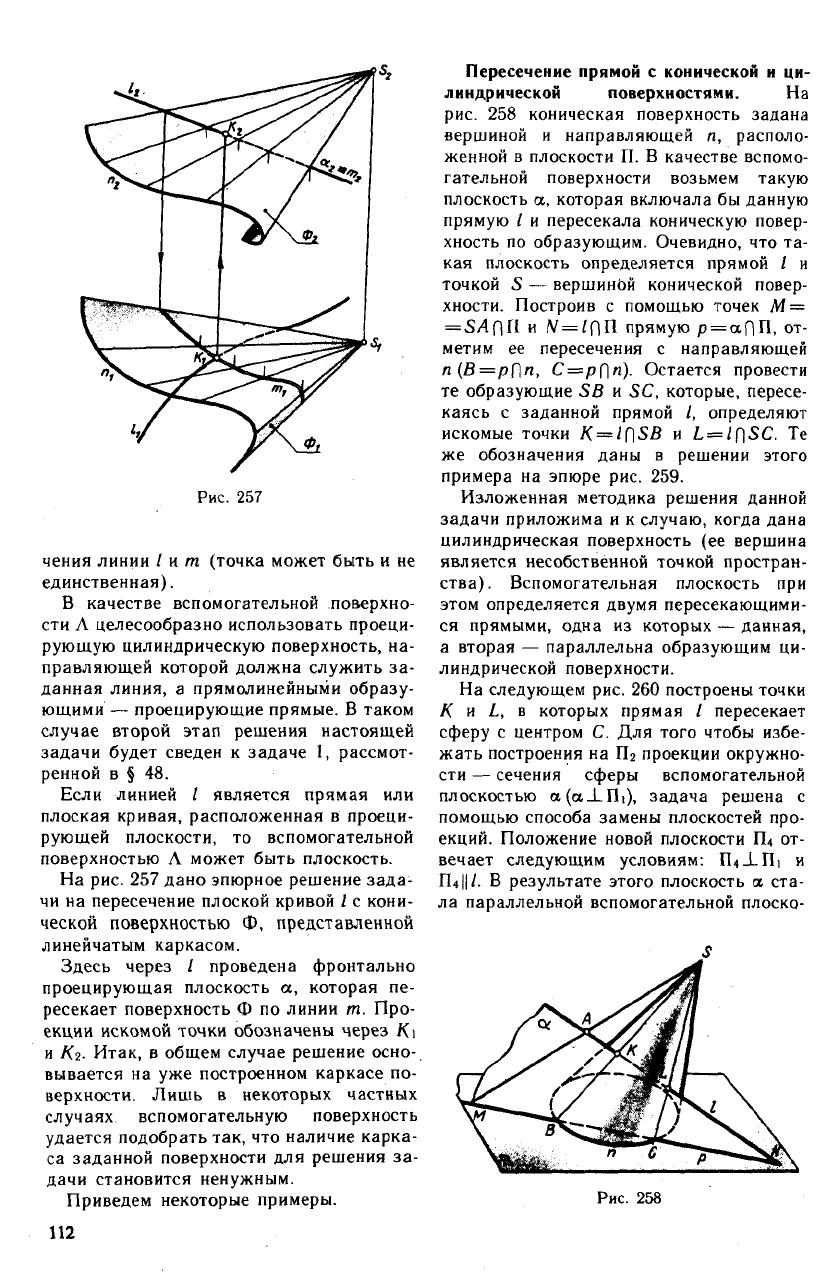
чения линии / и т (точка может быть и не

единственная).

В качестве вспомогательной поверхно-

сти Л целесообразно использовать проеци-

рующую цилиндрическую поверхность, на-

правляющей которой должна служить за-

данная линия, а прямолинейными образу-

ющими — проецирующие прямые. В таком

случае второй этап решения настоящей

задачи будет сведен к задаче 1, рассмот-

ренной в § 48.

Если линией I является прямая или

плоская кривая, расположенная в проеци-

рующей плоскости, то вспомогательной

поверхностью Л может быть плоскость.

На рис. 257 дано эпюрное решение зада-

чи на пересечение плоской кривой I с кони-

ческой поверхностью Ф, представленной

линейчатым каркасом.

Здесь через I проведена фронтально

проецирующая плоскость а, которая пе-

ресекает поверхность Ф по линии т. Про-

екции искомой точки обозначены через Кi

и Кг- Итак, в общем случае решение осно-

вывается на уже построенном каркасе по-

верхности. Лишь в некоторых частных

случаях вспомогательную поверхность

удается подобрать так, что наличие карка-

са заданной поверхности для решения за-

дачи становится ненужным.

Приведем некоторые примеры.

Пересечение прямой с конической и ци-

линдрической поверхностями. На

рис. 258 коническая поверхность задана

вершиной и направляющей п, располо-

женной в плоскости Г1. В качестве вспомо-

гательной поверхности возьмем такую

плоскость а, которая включала бы данную

прямую I и пересекала коническую повер-

хность по образующим. Очевидно, что та-

кая плоскость определяется прямой I и

точкой S — вершиной конической повер-

хности. Построив с помощью точек М =

= S/4fin и N = l(]U прямую р = аПП, от-

метим ее пересечения с направляющей

n(B=pf\n, C = pf\n). Остается провести

те образующие SB и SC, которые, пересе-

каясь с заданной прямой /, определяют

искомые точки K = lf\SB и

= if)SC. Те

же обозначения даны в решении этого

примера на эпюре рис. 259.

Изложенная методика решения данной

задачи приложима и к случаю, когда дана

цилиндрическая поверхность (ее вершина

является несобственной точкой простран-

ства). Вспомогательная плоскость при

этом определяется двумя пересекающими-

ся прямыми, одна из которых — данная,

а вторая — параллельна образующим ци-

линдрической поверхности.

На следующем рис. 260 построены точки

К и L, в которых прямая I пересекает

сферу с центром С. Для того чтобы избе-

жать построения на Пг проекции окружно-

сти — сечения сферы вспомогательной

плоскостью а(о1П|), задача решена с

помощью способа замены плоскостей про-

екций. Положение новой плоскости П

от-

вечает следующим условиям: П

-1_П1 и

||/. В результате этого плоскость а ста-

ла параллельной вспомогательной плоско-

Рис. 258

112

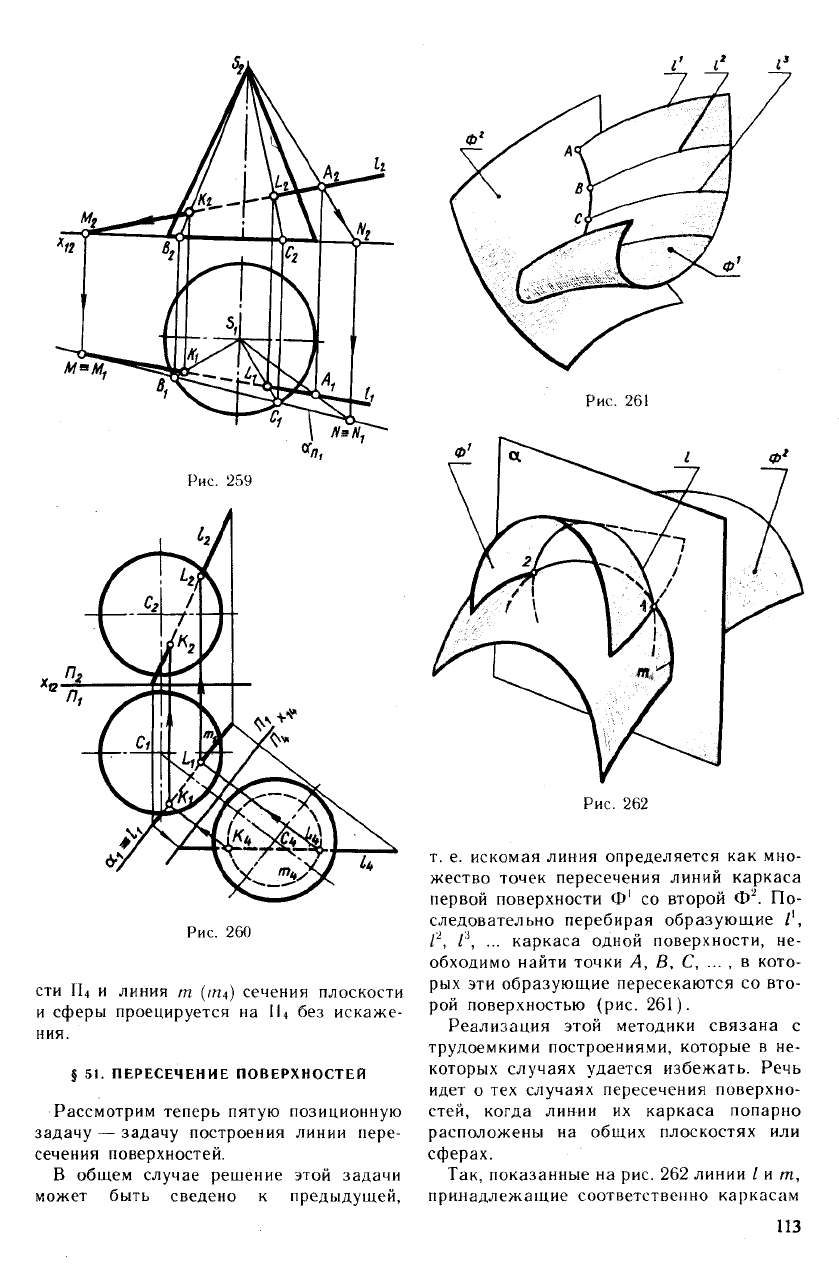
Рис. 260

сти II

и линия т (т

) сечения плоскости

и сферы проецируется на П

без искаже-

ния.

§ 51. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

Рассмотрим теперь пятую позиционную

задачу — задачу построения линии пере-

сечения поверхностей.

В общем случае решение этой задачи

может быть сведено к предыдущей,

т. е. искомая линия определяется как мно-

жество точек пересечения линий каркаса

первой поверхности Ф

со второй Ф

. По-

следовательно перебирая образующие /',

, 1\ ... каркаса одной поверхности, не-

обходимо найти точки А, В, С, ... , в кото-

рых эти образующие пересекаются со вто-

рой поверхностью (рис. 261).

Реализация этой методики связана с

трудоемкими построениями, которые в не-

которых случаях удается избежать. Речь

идет о тех случаях пересечения поверхно-

стей, когда линии их каркаса попарно

расположены на общих плоскостях или

сферах.

Так, показанные на рис. 262 линии / и т,

принадлежащие соответственно каркасам

113

поверхностей Ф

и Ф

, расположены на

одной плоскости а и определяют точки

/ и 2 искомой линии.

Построение таких каркасов легко осу-

ществить в некоторых случаях пересече-

ния линейчатых и циклических поверхно-

стей, которым посвящены следующие два

параграфа.

§ 52. СПОСОБ ПЛОСКИХ СЕЧЕНИЙ

Этот способ рекомендуется применять,

если сечениями заданных поверхностей

одной и той же плоскостью являются пря-

мые линии или окружности. Такая воз-

можность существует в трех случаях:

1. Если образующие (окружности) двух

циклических поверхностей расположены

в общих плоскостях уровня.

2. Если в общих плоскостях уровня ока-

зываются прямолинейные образующие ли-

нейчатой поверхности и окружности цик-

лической.

3. Линейчатые каркасы заданных повер-

хностей принадлежат общим плоскостям

уровня или пучкам плоскостей общего по-

ложения.

Рассмотрим примеры.

Пример I. Пересечение циклических по-

верхностей, образующие которых (окруж-

ности) расположены в общих плоскостях

уровня.

Пусть заданы две поверхности Ф

и Ф

первая из которых коническая *, вторая

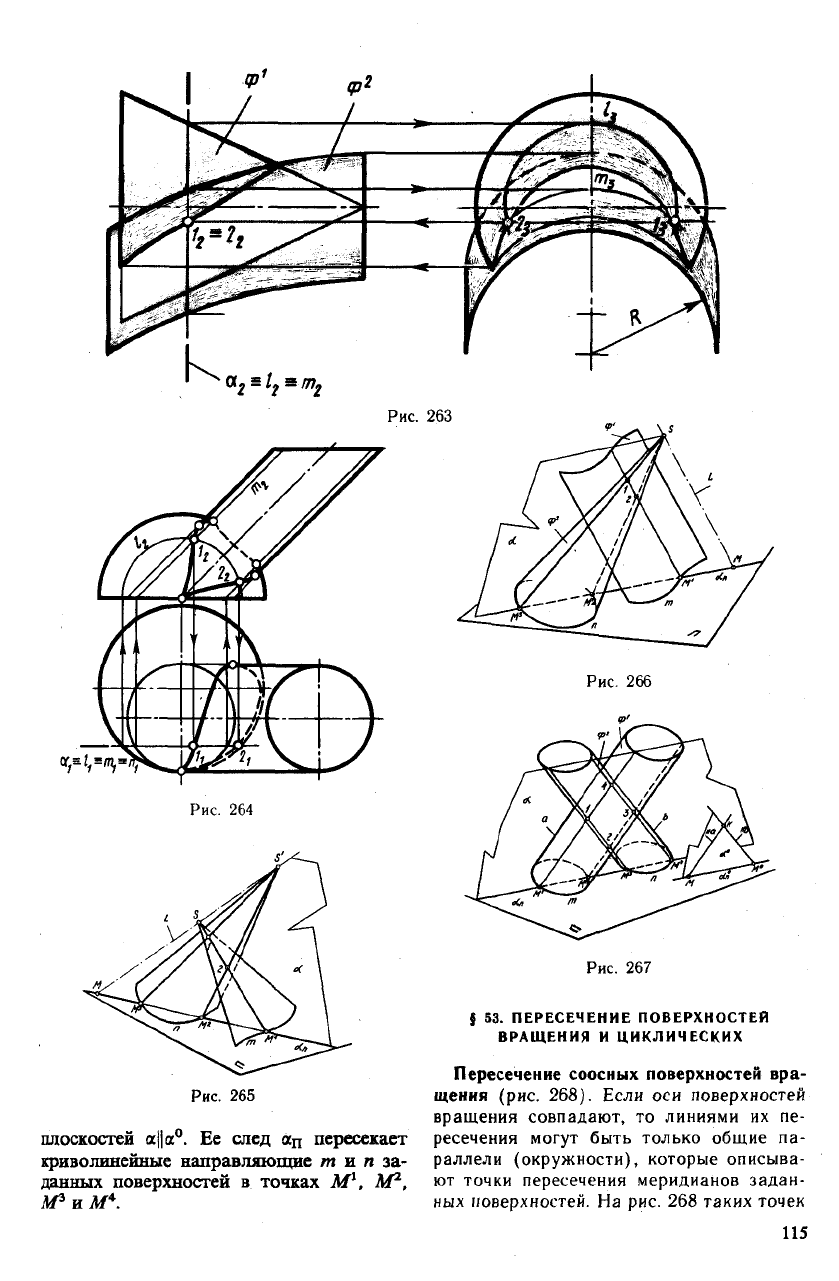
циклическая (рис. 262 и 263). Обе повер-

хности ориентированы так, что окружно-

сти их каркасов расположены в плоско-

стях, параллельных П

На рис. 262 и 263 показана только одна

пара таких окружностей / и т, располо-

женных в плоскости а. Их общие точки

1 и 2 (1 = lf\m, 2 = lf]m) принадлежат ли-

нии пересечения заданных поверхностей.

Переходя к другим парам окружностей,

аналогично получают остальные точки ис-

комой линии.

Пример 2. Пересечение сферы и эллип-

тического цилиндра.

* Коническая поверхность вращения пред-

ставляет собой частный случай циклической.

** На рис. 265 — 267 вспомогательные

секущие плоскости а следует считать прозрач-

ными.

В данном примере вспомогательные

плоскости уровня могут быть параллель-

ными плоскостям П

или IIj. В первом

случае (рис. 264) фронтальные плоскости

пересекают сферу по окружности, а ци-

линдр — по прямолинейным образу-

ющим. Одна из таких плоскостей пред-

ставлена своим горизонтальным следом

а,, а линии ее пересечения с заданными

поверхностями обозначены через 1(1^, /

) и л(л

). Точки

= lf]m

и 2=1 f\n принадлежат искомой кривой.

Нетрудно заметить, что плоскости, па-

раллельные П

пересекали бы каждую

поверхность по окружностям.

Пример 3. Пересечение конических

и цилиндрических поверхностей.

Пусть заданы две конические поверх-

ности, вершинами которых являются точ-

ки S и S

(рис. 265)**, а направляющими

служат соответственно линии лит, рас-

положенные в одной плоскости П. Их

линейчатые каркасы следует создавать

с помощью пучка плоскостей, носителем

которого должна быть прямая /, соединя-

ющая вершины S и S

. Одна из них, плос-

кость а (см. рис. 265), пересекает данные

поверхности по образующим (линиям ка-

ркаса) SM

, S^M

, Б

, точки 1 и 2 пере-

сечения которых и принадлежат искомой

линии.

Аналогично, с помощью пучка плоско-

стей строят и линии каркаса при пересече-

нии конической Ф

и цилиндрической Ф

поверхностей (рис. 266). Ось I пучха

в этом случае проходит через вершину

S конуса параллельно образующим цили-

ндра. Через М

, М

. М

обозначены точ-

ки пересечения следа плоскости осп с кри-

волинейными направляющими тип.

Наконец, если обе поверхности цилинд-

рические, то их линейчатые каркасы со-

здают с помощью плоскостей, параллель-

ных образующим как первой, так и вто-

рой поверхности. Направление следа

п (

=а

П) таких плоскостей устанав-

ливают построением плоскости паралле-

лизма а

(рис. 267), которая определяется

двумя пересекающимися в произвольной

точке К прямыми КМ и КМ

, соответст-

венно параллельными образующим пове-

рхностей Ф

и Ф

. Вспомогательные плос-

кости должны быть параллельны плоско-

]

ста а

. На рис. 267 показана одна из таких

114

^ а

я 1

а т

Рис.

плоскостей а||а°. Ее след а

пересекает

криволинейные направляющие т и п за-

данных поверхностей в точках М

, М

Л/

и М*.

Рис. 266

Рис. 267

§ 53. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

ВРАЩЕНИЯ И ЦИКЛИЧЕСКИХ

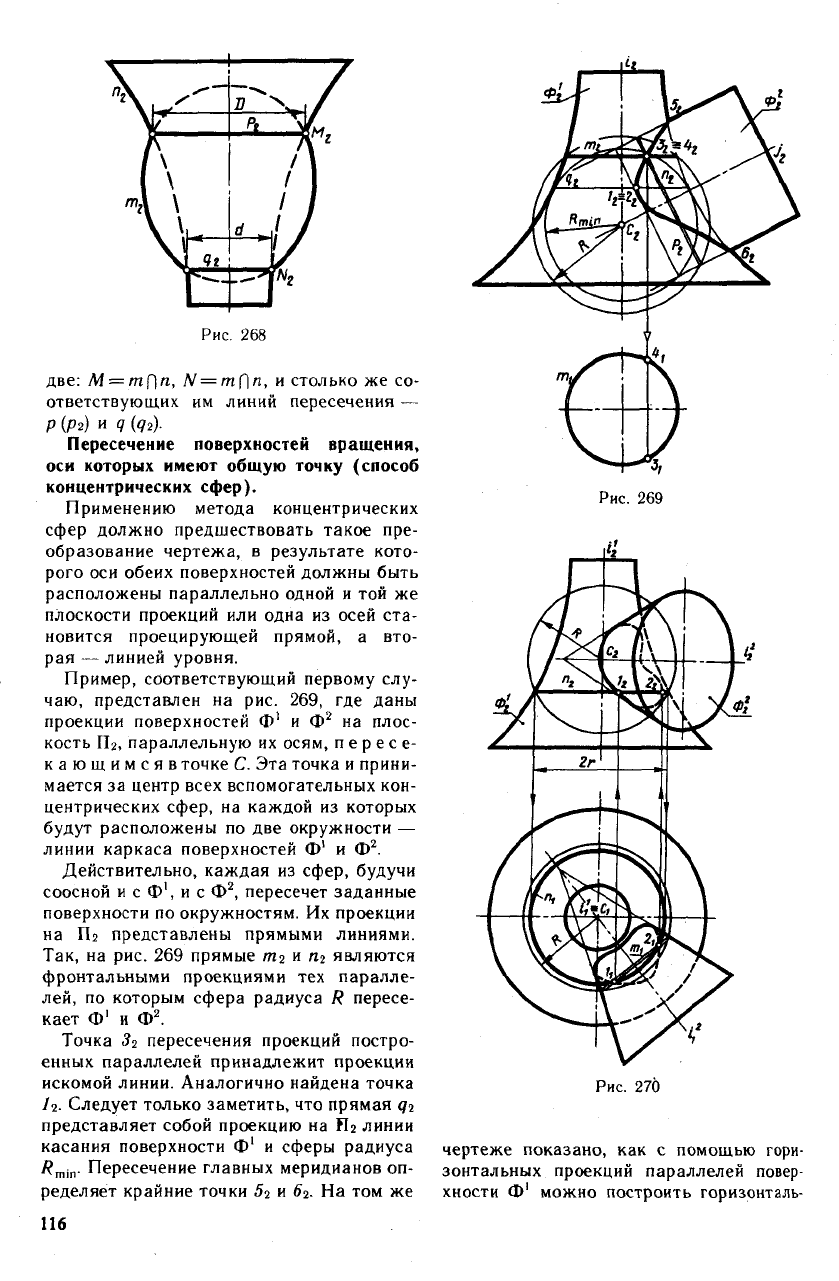
Пересечение соосных поверхностей вра-

щения (рис. 268). Если оси поверхностей

вращения совпадают, то линиями их пе-

ресечения могут быть только общие па-

раллели (окружности), которые описыва-

ют точки пересечения меридианов задан-

ных поверхностей. На рис. 268 таких точек

115

/77,

d J J

Чг

Рис. 268

две: М = тП", N = mfln, и столько же со-

ответствующих им линий пересечения —

Р (Рг) и q Ы-

Пересечение поверхностей вращения,

оси которых имеют общую точку (способ

концентрических сфер).

Применению метода концентрических

сфер должно предшествовать такое пре-

образование чертежа, в результате кото-

рого оси обеих поверхностей должны быть

расположены параллельно одной и той же

плоскости проекций или одна из осей ста-

новится проецирующей прямой, а вто-

рая — линией уровня.

Пример, соответствующий первому слу-

чаю, представлен на рис. 269, где даны

проекции поверхностей Ф

и Ф

на плос-

кость Пг, параллельную их осям, Пересе-

кающимсяв точке С. Эта точка и прини-

мается за центр всех вспомогательных кон-

центрических сфер, на каждой из которых

будут расположены по две окружности —

линии каркаса поверхностей Ф

и Ф

Действительно, каждая из сфер, будучи

соосной и с Ф', и с Ф

, пересечет заданные

поверхности по окружностям. Их проекции

на Пг представлены прямыми линиями.

Так, на рис. 269 прямые т

и п

являются

фронтальными проекциями тех паралле-

лей, по которым сфера радиуса R пересе-

кает Ф

и Ф

Точка 3

пересечения проекций постро-

енных параллелей принадлежит проекции

искомой линии. Аналогично найдена точка

. Следует только заметить, что прямая q

представляет собой проекцию на П

линии

касания поверхности Ф

и сферы радиуса

min

. Пересечение главных меридианов оп-

ределяет крайние точки 5

и 6

. На том же

Рис. 270

чертеже показано, как с помощью гори-

зонтальных проекций параллелей повер-

хности Ф

можно построить горизонталь-

116

ные проекции найденных точек (см. гори-

зонтальные проекции точек 3 и 4).

В качестве второго примера на примене-

ние способа концентрических сфер рас-

смотрим пересечение поверхностей враще-

ния Ф

и Ф

(рис. 270-), ось первой из

которых является горизонтально проеци-

рующей прямой (t'_LIIi), а ось i

кониче-

ской поверхности — линией уровня

Hi).

Точки / и 2 искомой линии построены

с помощью сферы радиуса R с центром

в точке C = t' f]i'

Эта сфера пересекает поверхность Ф

по

окружности л радиуса г, а коническую

поверхность Ф

— по окружности т, кото-

рая показана только на горизонтальной

проекции (прямая т\).

Пересечение горизонтальных проекций

окружностей п.\ и т\ определяют проекции

и 2\ точек искомой линии. Их фронталь-

ные проекции /

и 2г построены на пере-

сечении л 2 с линиями проекционной

связи.

Изменяя радиус R вспомогательной

сферы, создают новые пары окружностей

каркасов заданных поверхностей и анало-

гично определяют остальные точки линии

пересечения.

Пересечение поверхности вращения и

циклической, линия центров которой рас-

положена в общей плоскости симметрии

заданных поверхностей.

Если две циклические поверхности, одна

из которых является поверхностью враще-

ния, имеют общую плоскость симметрии,

включающую линию центров циклической

поверхности, то .линия их пересечения мо-

жет быть построена способом эк-

сцентрических сфер.

Рассмотрим сущность этого способа на

примере пересечения цилиндрической

поверхности Ф

и циклической Ф

(рис. 27Г).

Обе поверхности имеют общую плос-

кость симметрии, в которой расположены

ось цилиндра i, линия центров цикличе-

ской поверхности и точки 1 и 2, принадле-

жащие очерковым линиям.

Покажем, что можно построить сферы,

каждая из которых пересечет заданные

поверхности по окружности.

Прежде всего выделим из каркаса цик-

лической поверхности одну окружность

Рис. 271

(ее фронтальная проекция на рис. 271

обозначена через т

Центры всех сфер, которые можно про-

вести через эту окружность, будут распо-

ложены на прямой р (pi), проходящей че-

рез центр С (С

) рассматриваемой окруж-

ности перпендикулярно ее плоскости а.

Прямая р, находясь в общей плоскости

симметрии, пересечет ось / цилиндра в точ-

ке О (Ог) — центре той вспомогательной

сферы радиуса R, на поверхности которой

окажутся две окружности: выделенная из

каркаса циклической поверхности и па-

раллель л (п

) цилиндра.

Обе окружности, находясь на одной

сфере, в общем случае пересекаются в

двух точках 3 и 4. Их фронтальные проек-

ции 3

и 4

окажутся совмещенными с

точкой пересечения проекций т

и п

ок-

ружностей — линий каркаса поверхностей

Ф' и Ф

Переходя к следующим окружностям

каркаса циклической поверхности и повто-

ряя описанное выше построение, можно

получить множество точек, принадлежа-

щих искомой линии пересечения рассмат-

риваемых поверхностей. Заметим, что цен-

тры всех вспомогательных эксцентриче-

ских сфер будут расположены на оси

поверхности вращения.

§ 54. ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ

ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

Поверхностью второго порядка называ-

ется множество точек пространства, де-

картовы координаты которых удовлетво-

117

ряют алгебраическому уравнению второй

степени.

Это уравнение можно записать в следу-

ющем виде:

а,

,д:

+ а

+ a

+ 2а

xy + 2а,

xz +

-\-2a

yz + a

x-\-a

y-\-a

z + a = 0. (9.1)

Две поверхности второго порядка в об-

щем случае пересекаются по простран-

ственной линии четвертого порядка, кото-

рую называют биквадратной кри-

вой.

В некоторых частных случаях биквад-

ратная кривая распадается на две плоские

кривые второго порядка, причем одна из

них может быть мнимой.

Опуская доказательства *, приведем не-

которые теоремы и примеры, иллюстриру-

ющие их применение.

Теорема 1. Если две поверхности второ-

го порядка пересекаются по одной плоской

кривой, то существует и другая плоская

кривая, по которой они пересекаются.

Рассмотрим пример, к которому прило-

жима эта теорема.

На рис. 272 изображены фронтальные

проекции Ф

сферы Ф и 6г эллиптического

цилиндра в, имеющих общую окружность

m (m

) с центром О (Ог).

Плоскость а, определяемая центром

С сферы и осью i цилиндра, является

плоскостью симметрии заданных повер-

хностей (о

Пг).

Общая окружность радиуса г — это од-

на из плоских кривых второго порядка

распавшейся линии пересечения. Остается

построить вторую кривую, плоскость ct

которой должна быть в условиях данного

примера перпендикулярна плоскости сим-

метрии а, а следовательно, и П

(a -L Пг).

Вторая линия пересечения (окружность)

спроецируется на П

в виде отрезка прямой

. Для его построения следует воспользо-

ваться точками Аг и Вг, принадлежащими

очеркам заданных поверхностей.

Теорема 2 (о двойном касании) **. Если

* С доказательством можно ознакомиться по

книге [20].

** Две поверхности, имеющие в общей точке

общую касательную плоскость, называются с о-

прикасаюшимися. Поверхности, соприка-

сающиеся в двух точках, имеют двойное касание.

две поверхности второго порядка имеют

касание в двух точках А и В,

то

линия их

пересечения распадается на две плоские

кривые второго порядка, плоскости кото-

рых проходят через отрезок прямой АВ,

соединяющей точки касания.

Например, по двум окружностям тип

пересекается сфера Ф с поверхностью эл-

липтического цилиндра 9, изображенные

на рис. 273. Точки касания и касательные

плоскости обозначены соответственно че-

рез А, В, аэЛ, рэВ. Окружности, на

которые распалась линия пересечения по-

верхностей, расположены во фронтально

проецирующих плоскостях уэт и бэя.

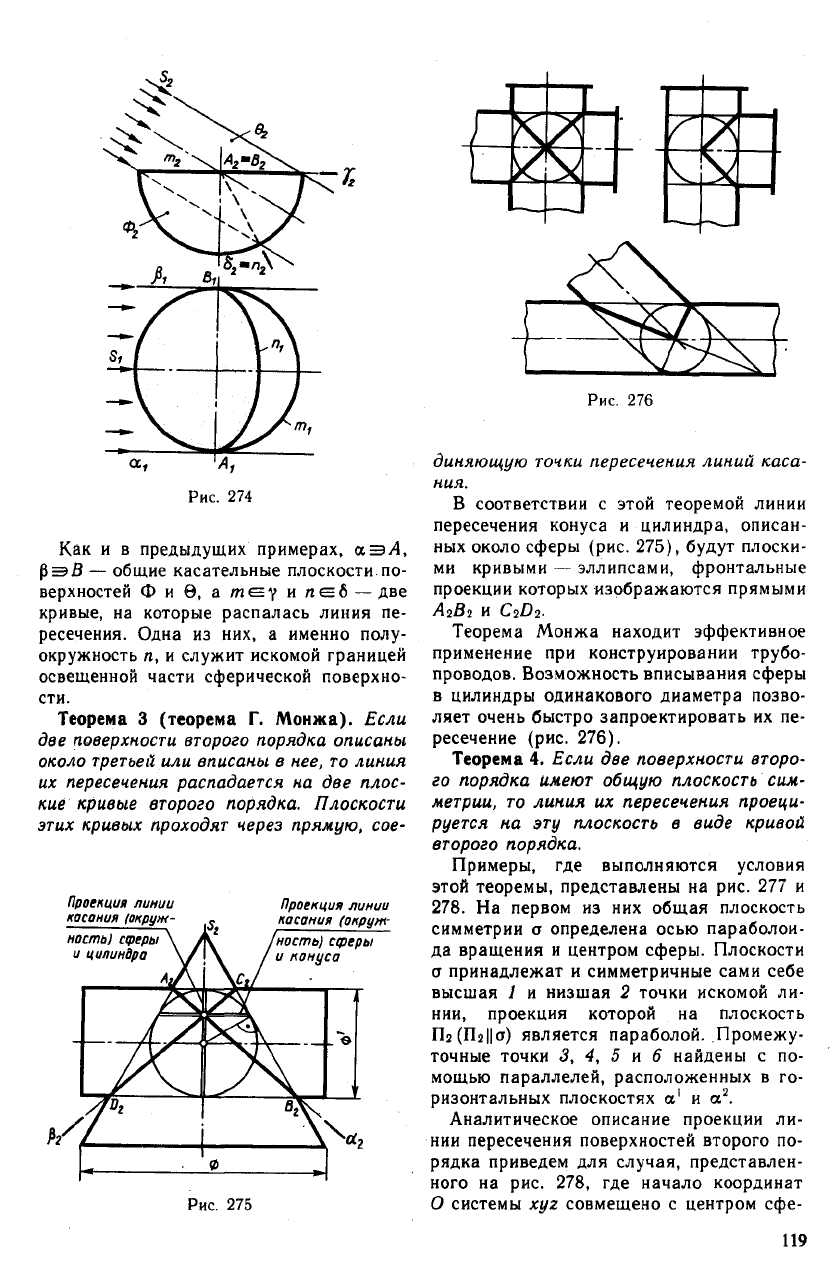
Только что рассмотренному примеру

можно дать иное содержание, поставив

следующую задачу: при заданном направ-

лении световых лучей определить границу

освещенной части внутренней поверхности

Ф сферической чаши (рис. 274).

Световые лучи, проходящие через эква-

тор m сферической чаши, образуют линей-

чатую поверхность эллиптического цилин-

дра в, который касается полусферы Ф

в точках Л и В.

Ф,

Рис. 273

Проекция линии

касания Iокрум-

насты сферы

и цилиндра

Проекция линии

касания (окруж-

ность) сферы

и конуса

Рис. 274

Как и в предыдущих примерах, аЭ/4,

рэВ — общие касательные плоскости по-

верхностей Фив, а те| и neS — две

кривые, на которые распалась линия пе-

ресечения. Одна из них, а именно полу-

окружность л, и служит искомой границей

освещенной части сферической поверхно-

сти.

Теорема 3 (теорема Г. Монжа). Если

две поверхности второго порядка описаны

около третьей или вписаны в нее, то линия

их пересечения распадается на две плос-

кие кривые второго порядка. Плоскости

этих кривых проходят через прямую, сое-

Рис. 258

Рис. 276

диняющую точки пересечения линий каса-

ния.

В соответствии с этой теоремой линии

пересечения конуса и цилиндра, описан-

ных около сферы (рис. 275), будут плоски-

ми кривыми — эллипсами, фронтальные

проекции которых изображаются прямыми

и C

Теорема Монжа находит эффективное

применение при конструировании трубо-

проводов. Возможность вписывания сферы

в цилиндры одинакового диаметра позво-

ляет очень быстро запроектировать их пе-

ресечение (рис. 276).

Теорема 4. Если две поверхности второ-

го порядка имеют общую плоскость сим-

метрии, то линия их пересечения проеци-

руется на эту плоскость в виде кривой

второго порядка.

Примеры, где выполняются условия

этой теоремы, представлены на рис. 277 и

278. На первом из них общая плоскость

симметрии о определена осью параболои-

да вращения и центром сферы. Плоскости

а принадлежат и симметричные сами себе

высшая 1 и низшая 2 точки искомой ли-

нии, проекция которой на плоскость

П2(Пг||а) является параболой. Промежу-

точные точки 3, 4, 5 и 6 найдены с по-

мощью параллелей, расположенных в го-

ризонтальных плоскостях а

и а

Аналитическое описание проекции ли-

нии пересечения поверхностей второго по-

рядка приведем для случая, представлен-

ного на рис. 278, где начало координат

О системы хуг совмещено с центром сфе-

119