Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

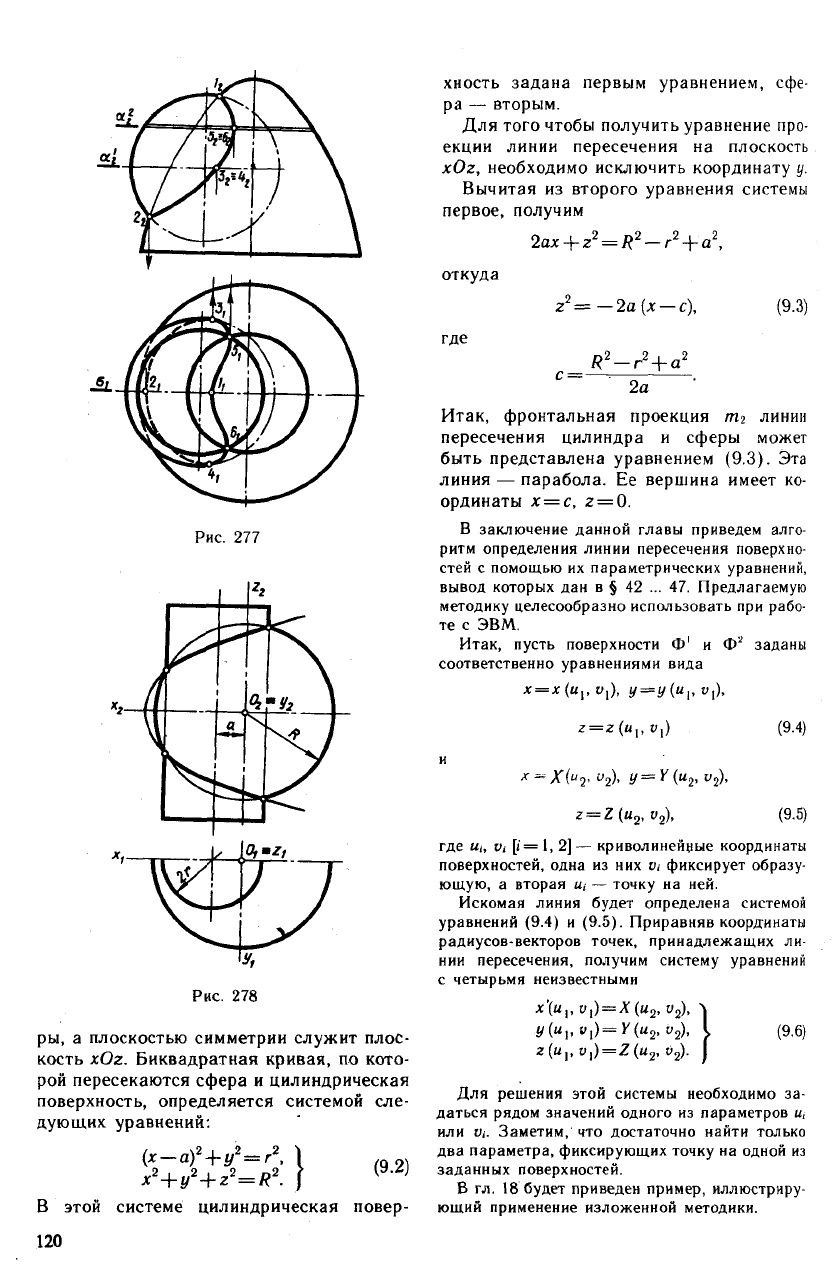
Рис. 277

ры, а плоскостью симметрии служит плос-

кость xOz. Биквадратная кривая, по кото-

рой пересекаются сфера и цилиндрическая

поверхность, определяется системой сле-

дующих уравнений:

(х — af + y

, \

(q<2)

В этой системе цилиндрическая повер-

хность задана первым уравнением, сфе-

ра — вторым.

Для того чтобы получить уравнение про-

екции линии пересечения на плоскость

хOz, необходимо исключить координату у.

Вычитая из второго уравнения системы

первое, получим

2ax + z

= R

— л

+ а

откуда

= -2а (х — с), (9.3)

где

-г

+а

С = : .

2 а

Итак, фронтальная проекция т.2 линии

пересечения цилиндра и сферы может

быть представлена уравнением (9.3). Эта

линия — парабола. Ее вершина имеет ко-

ординаты х = с, z = 0.

В заключение данной главы приведем алго-

ритм определения линии пересечения поверхно-

стей с помощью их параметрических уравнений,

вывод которых дан в § 42 ... 47. Предлагаемую

методику целесообразно использовать при рабо-

те с ЭВМ.

Итак, пусть поверхности Ф

и Ф

заданы

соответственно уравнениями вида

х = х (и,, у,), у = I/ (uj, у,),

z = z(u,,y,) (9.4)

~ XI

2)' У—У (И

, У

z = Z (и

, у

), (9.5)

где Ui, Vi [i= 1, 2]— криволинейные координаты

поверхностей, одна из них у, фиксирует образу-

ющую, а вторая и, — точку на ней.

Искомая линия будет определена системой

уравнений (9.4) и (9.5). Приравняв координаты

радиусов-векторов точек, принадлежащих ли-

нии пересечения, получим систему уравнений

с четырьмя неизвестными

х\и

{

, У,) = *(и

, У

), ^

i/(u

)=K(u

, v

), I (9.6)

z(u,, y,) = Z(u

, У

). j

Для решения этой системы необходимо за-

даться рядом значений одного из параметров Ц;

или Vi. Заметим, что достаточно найти только

два параметра, фиксирующих точку на одной из

заданных поверхностей.

В гл. 18 будет приведен пример, иллюстриру-

ющий применение изложенной методики.

120

Вопросы и задачи

для самоконтроля

1. Перечислите графические операции при

построении плоских сечений любой поверх-

ности.

2. Назовите три этапа решения задачи на

пересечение прямой линии с поверхностью.

3. При каких условиях линия пересечения

поверхностей может быть построена с помощью

концентрических сфер?

4. Перечислите условия, при выполнении ко-

торых можно применять способ эксцентрических

сфер.

5. Что представляет собой множество центров

пучка сфер, под которым понимают сферы, пе-

ресекающиеся по одной окружности?

6. Как построить плоскость, которая проходит

через данную прямую I и пересекает конус вра-

щения по параболе?

7. На поверхности сферы определить точки,

равноудаленные от трех заданных точек, распо-

ложенных вне сферы.

8. При каком условии две поверхности враще-

ния общего вида могут иметь общую плоскость

симметрии?

9. В каких случаях линия пересечения повер-

хностей второго порядка распадается на две

плоские кривые?

10. Как определить точки, удаленные на рас-

стояние а мм от каждой из трех пересекающих-

ся прямых, не принадлежащих одной плоско-

сти?

11. На кривой линии I определить точку,

ближайшую к поверхности вращения (рис.

279).

12. Как на данной прямой определить точки,

удаленные от поверхности вращения на рассто-

ГЛАВА 10

ПЛОСКОСТИ, КАСАТЕЛЬНЫЕ

К КРИВЫМ ПОВЕРХНОСТЯМ

В дифференциальной геометрии доказы-

вается, что касательная плоскость к по-

верхности Ф в точке А представляет собой

множество прямых, касательных к любым

кривым, проходящим по поверхности через

данную точку.

Следовательно, положение плоскости ос,

касательной к поверхности в данной точ-

ке А, можно определить двумя прямыми

а и Ь, каждая из которых является каса-

тельной к кривой, проведенной по повер-

хности через точку А. На рис. 280 прямые

а и b — касательные к кривым /' и f

Примеры, которые будут рассмотрены

ниже, покажут, что плоскость может ка-

саться поверхности либо в точке, либо по

линии (прямой или плоской кривой). Ка-

саясь поверхности в данной точке, плос-

кость может пересекать поверхность по

одной или двум линиям. На поверхности

могут быть точки, в которых либо нельзя

провести касательную плоскость, либо ка-

сательная плоскость не определяется

единственным образом. Такие точки назы-

ваются особыми. К их числу относятся

точки самопересечения поверхности, точки

ребра возврата, заостренные вершины по-

верхностей вращения (когда образующая

пересекает ось вращения не под прямым

углом).

Точки, в которых можно провести един-

ственную касательную плоскость, называ-

ются обыкновенными. Наконец, вве-

дем еще одно понятие — нормаль к по-

121

верхности. Так называется прямая,

перпендикулярная касательной плоскости

и проходящая через точку касания. Оче-

видно, что задачи на построение нормалей

к кривым поверхностям можно свести к

задачам на построение касательных плос-

костей.

f 55. КАСАТЕЛЬНЫЕ ПЛОСКОСТИ

К ЛИНЕЙЧАТЫМ ПОВЕРХНОСТЯМ

Линейчатые поверхности представляют

собой множество прямых линий — образу-

ющих. Плоскость, касательная к линейча-

той поверхности в произвольной точке на

данной образующей, проходит через эту

образующую. Сказанное объясняется тем,

что каждая образующая является своей

собственной касательной.

Рис. 258

122

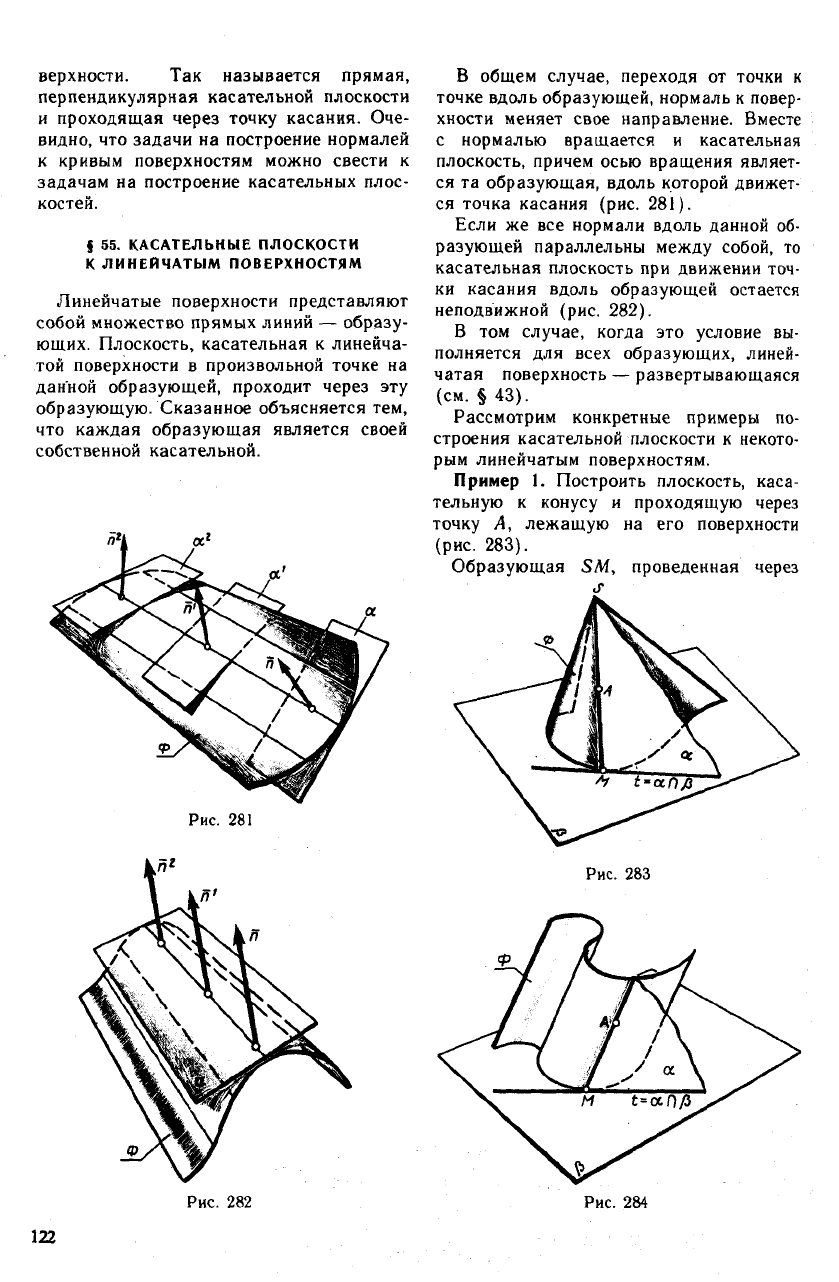
В общем случае, переходя от точки к

точке вдоль образующей, нормаль к повер-

хности меняет свое направление. Вместе

с нормалью вращается и касательная

плоскость, причем осью вращения являет-

ся та образующая, вдоль которой движет-

ся точка касания (рис. 281).

Если же все нормали вдоль данной об-

разующей параллельны между собой, то

касательная плоскость при движении точ-

ки касания вдоль образующей остается

неподвижной (рис. 282).

В том случае, когда это условие вы-

полняется для всех образующих, линей-

чатая поверхность — развертывающаяся

(см. § 43).

Рассмотрим конкретные примеры по-

строения касательной плоскости к некото-

рым линейчатым поверхностям.

Пример 1. Построить плоскость, каса-

тельную к конусу и проходящую через

точку А, лежащую на его поверхности

(рис. 283).

Образующая SM, проведенная через

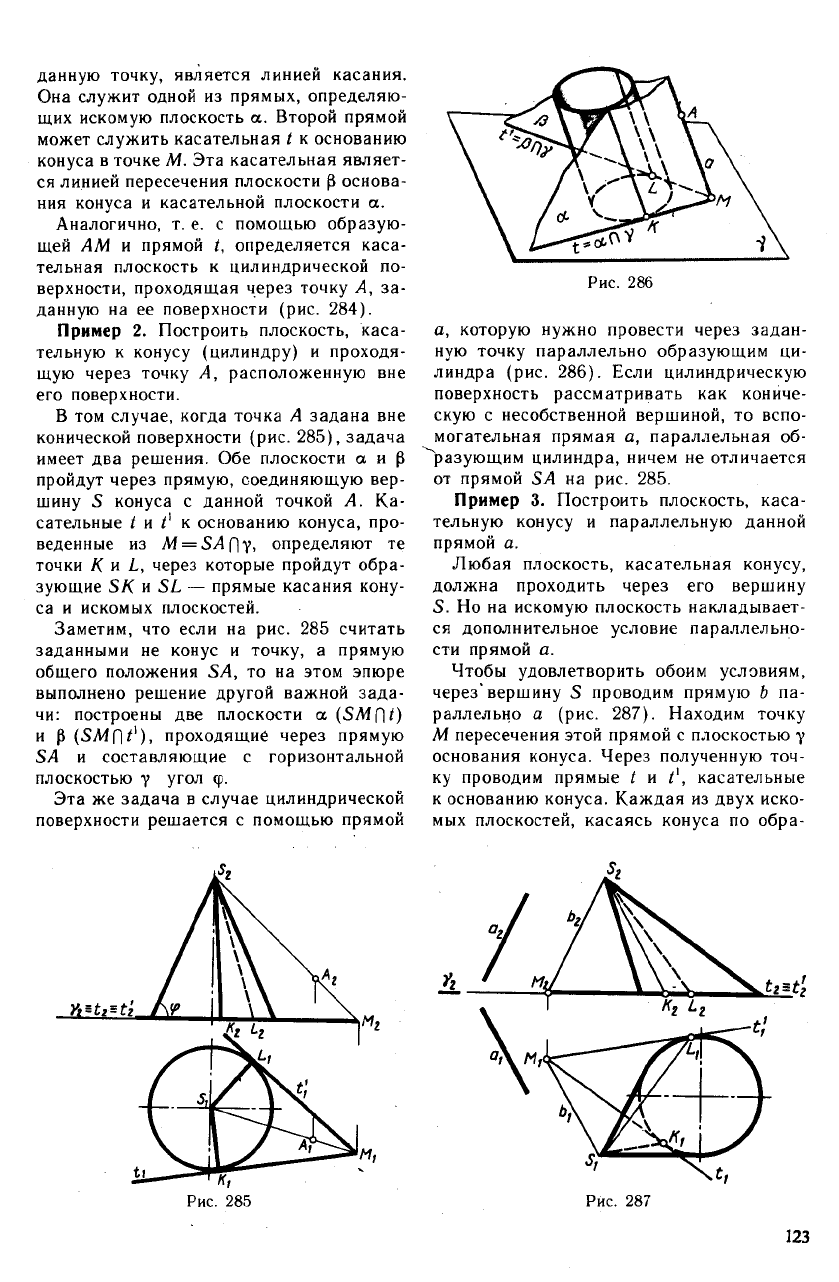
данную точку, является линией касания.

Она служит одной из прямых, определяю-

щих искомую плоскость а. Второй прямой

может служить касательная t к основанию

конуса в точке М. Эта касательная являет-

ся линией пересечения плоскости р основа-

ния конуса и касательной плоскости а.

Аналогично, т. е. с помощью образую-

щей AM и прямой t, определяется каса-

тельная плоскость к цилиндрической по-

верхности, проходящая через точку А, за-

данную на ее поверхности (рис. 284).

Пример 2. Построить плоскость, каса-

тельную к конусу (цилиндру) и проходя-

щую через точку А, расположенную вне

его поверхности.

В том случае, когда точка А задана вне

конической поверхности (рис. 285), задача

имеет два решения. Обе плоскости аир

пройдут через прямую, соединяющую вер-

шину S конуса с данной точкой А. Ка-

сательные t и к основанию конуса, про-

веденные из M = Si4nv. определяют те

точки К и L, через которые пройдут обра-

зующие SK и SL — прямые касания кону-

са и искомых плоскостей.

Заметим, что если на рис. 285 считать

заданными не конус и точку, а прямую

общего положения S/1, то на этом эпюре

выполнено решение другой важной зада-

чи: построены две плоскости a(SMflO

и р (SAtffU

). проходящие через прямую

S-4 и составляющие с горизонтальной

плоскостью у угол ф.

Эта же задача в случае цилиндрической

поверхности решается с помощью прямой

а, которую нужно провести через задан-

ную точку параллельно образующим ци-

линдра (рис. 286). Если цилиндрическую

поверхность рассматривать как кониче-

скую с несобственной вершиной, то вспо-

могательная прямая а, параллельная об-

разующим цилиндра, ничем не отличается

от прямой SJ4 на рис. 285.

Пример 3. Построить плоскость, каса-

тельную конусу и параллельную данной

прямой о.

Любая плоскость, касательная конусу,

должна проходить через его вершину

S. Но на искомую плоскость накладывает-

ся дополнительное условие параллельно-

сти прямой а.

Чтобы удовлетворить обоим условиям,

через'вершину S проводим прямую b па-

раллельно а (рис. 287). Находим точку

М пересечения этой прямой с плоскостью у

основания конуса. Через полученную точ-

ку проводим прямые t и касательные

к основанию конуса. Каждая из двух иско-

мых плоскостей, касаясь конуса по обра-

123

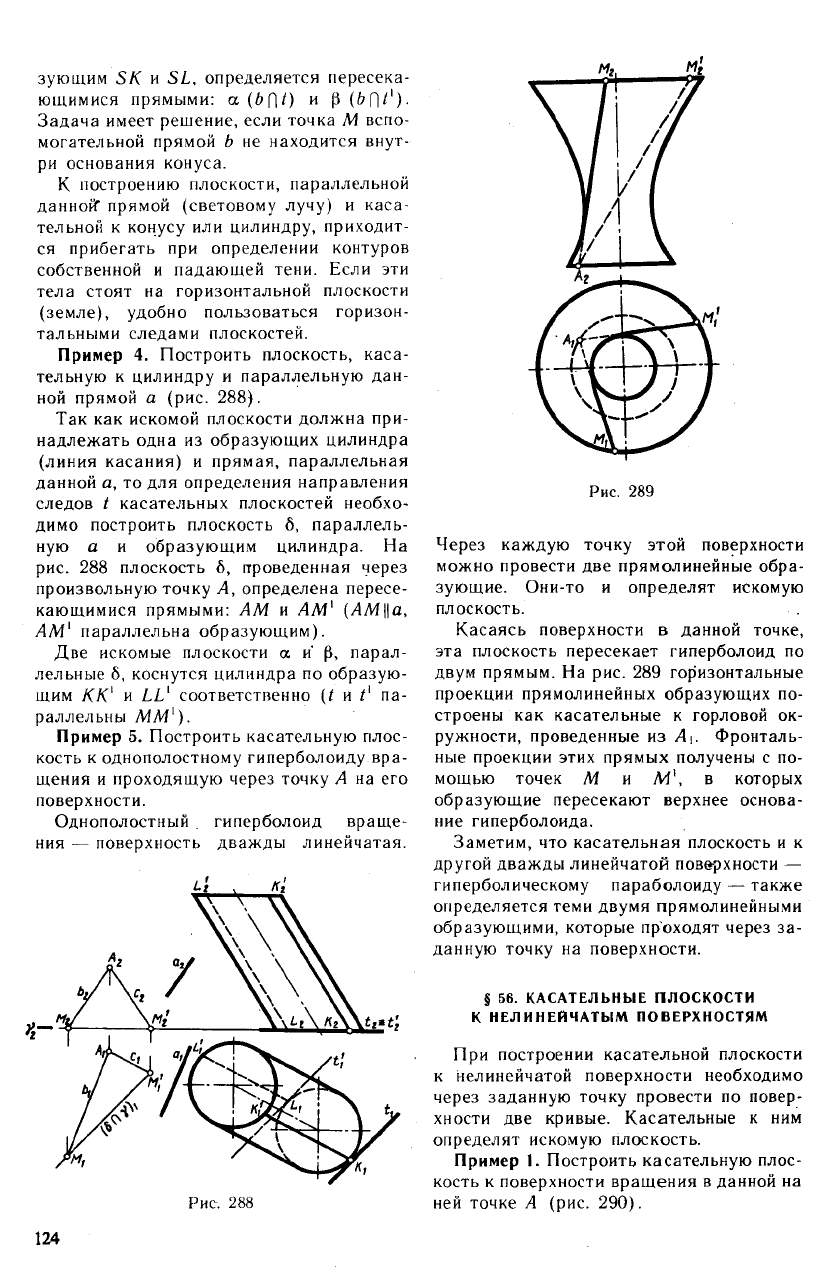
зующим SK и SL, определяется пересека-

ющимися прямыми: a (b[\t) и p(&f|*')-

Задача имеет решение, если точка М вспо-

могательной прямой b не находится внут-

ри основания конуса.

К построению плоскости, параллельной

данной" прямой (световому лучу) и каса-

тельной к конусу или цилиндру, приходит-

ся прибегать при определении контуров

собственной и падающей тени. Если эти

тела стоят на горизонтальной плоскости

(земле), удобно пользоваться горизон-

тальными следами плоскостей.

Пример 4. Построить плоскость, каса-

тельную к цилиндру и параллельную дан-

ной прямой а (рис. 288).

Так как искомой плоскости должна при-

надлежать одна из образующих цилиндра

(линия касания) и прямая, параллельная

данной а, то для определения направления

следов t касательных плоскостей необхо-

димо построить плоскость 6, параллель-

ную а и образующим цилиндра. На

рис. 288 плоскость б, проведенная через

произвольную точку А, определена пересе-

кающимися прямыми: AM и AM

(АМ\\а,

АМ

{

параллельна образующим).

Две искомые плоскости ос и' р, парал-

лельные 6, коснутся цилиндра по образую-

щим КК' и LL' соответственно (t и па-

раллельны ММ

Пример 5. Построить касательную плос-

кость к однополостному гиперболоиду вра-

щения и проходящую через точку А на его

поверхности.

Однополостный . гиперболоид враще-

ния — поверхность дважды линейчатая.

н-

Рис. 288

Рис. 289

Через каждую точку этой поверхности

можно провести две прямолинейные обра-

зующие. Они-то и определят искомую

плоскость.

Касаясь поверхности в данной точке,

эта плоскость пересекает гиперболоид по

двум прямым. На рис. 289 горизонтальные

проекции прямолинейных образующих по-

строены как касательные к горловой ок-

ружности, проведенные из At. Фронталь-

ные проекции этих прямых получены с по-

мощью точек М и М\ в которых

образующие пересекают верхнее основа-

ние гиперболоида.

Заметим, что касательная плоскость и к

другой дважды линейчатой поверхности —

гиперболическому параболоиду — также

определяется теми двумя прямолинейными

образующими, которые проходят через за-

данную точку на поверхности.

§ 56. КАСАТЕЛЬНЫЕ ПЛОСКОСТИ

К НЕЛИНЕЙЧАТЫМ ПОВЕРХНОСТЯМ

При построении касательной плоскости

к нелинейчатой поверхности необходимо

через заданную точку провести по повер-

хности две кривые. Касательные к ним

определят искомую плоскость.

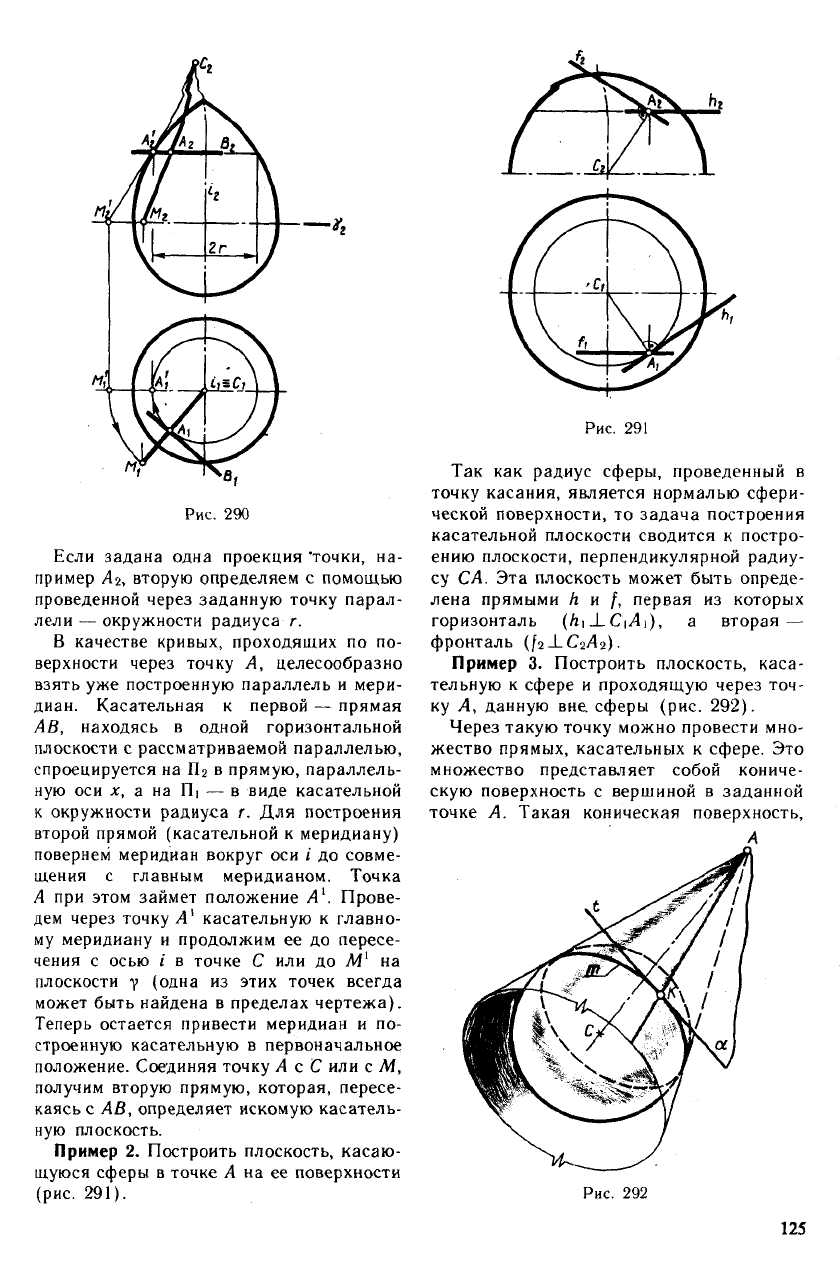
Пример 1. Построить касательную плос-

кость к поверхности вращения в данной на

ней точке А (рис. 290).

124

'г

Zr ,

Рис. 290

Если задана одна проекция "точки, на-

пример Лг, вторую определяем с помощью

проведенной через заданную точку парал-

лели — окружности радиуса г.

В качестве кривых, проходящих по по-

верхности через точку Л, целесообразно

взять уже построенную параллель и мери-

диан. Касательная к первой — прямая

АВ, находясь в одной горизонтальной

плоскости с рассматриваемой параллелью,

спроецируется на Пг в прямую, параллель-

ную оси х, а на

11|

— в виде касательной

к окружности радиуса г. Для построения

второй прямой (касательной к меридиану)

повернем меридиан вокруг оси i до совме-

щения с главным меридианом. Точка

А при этом займет положение Л'. Прове-

дем через точку Л

касательную к главно-

му меридиану и продолжим ее до пересе-

чения с осью i в точке С или до М

на

плоскости у (одна из этих точек всегда

может быть найдена в пределах чертежа).

Теперь остается привести меридиан и по-

строенную касательную в первоначальное

положение. Соединяя точку Л с С или с М,

получим вторую прямую, которая, пересе-

каясь с АВ, определяет искомую касатель-

ную плоскость.

Пример 2. Построить плоскость, касаю-

щуюся сферы в точке Л на ее поверхности

(рис. 291).

Рис. 291

Так как радиус сферы, проведенный в

точку касания, является нормалью сфери-

ческой поверхности, то задача построения

касательной плоскости сводится к постро-

ению плоскости, перпендикулярной радиу-

су СЛ. Эта плоскость может быть опреде-

лена прямыми Ли/, первая из которых

горизонталь (Л1_1_С|Л|), а вторая —

фронталь ^2-1_С

Пример 3. Построить плоскость, каса-

тельную к сфере и проходящую через точ-

ку Л, данную вне сферы (рис. 292).

Через такую точку можно провести мно-

жество прямых, касательных к сфере. Это

множество представляет собой кониче-

скую поверхность с вершиной в заданной

точке Л. Такая коническая поверхность,

Рис. 292

125

описанная вокруг сферы, касается ее по

окружности т. Вместе с тем любая плос-

кость а, касательная к конусу, касается

и сферы. Действительно, у плоскости

а (ЛКПО

сферы имеется только одна

общая точка К — точка касания. Задача,

таким образом, допускает множество ре-

шений.

Искомые плоскости легко построить, ес-

ли прямая, соединяющая точку А и центр

сферы С, перпендикулярна одной из плос-

костей проекций. В случае, когда АС —

прямая общего положения, необходимо

преобразовать эпюр с таким расчетом,

чтобы одна из проекций прямой АС оказа-

лась точкой. Решение завершается постро-

ением плоскости, касательной к вспомога-

тельному прямому круговому конусу.

Вопросы и задачи для самоконтроля

1. Как можно построить касательную плос-

кость к дважды линейчатой поверхности (одно-

полостному гиперболоиду и гиперболическому

параболоиду)?

2. Через прямую линию общего положения

провести плоскость, расположенную под задан-

ным углом к плоскости проекции П]. При каком

соотношении углов наклона прямой и плоскости

к Ш возможно решение этой задачи?

3. Построить плоскость, касательную к сфере

и равнонаклоненную к трем плоскостям проек-

ций.

4. Построить плоскость, касающуюся конуса

и сферы.

5. Как построить плоскость, которая касает-

ся конуса и параллельна данной прямой?

6. Могут ли две линейчатые поверхности,

одна из которых развертывающаяся, а другая

неразвертывающаяся, взаимно касаться по пря-

молинейной образующей?

7. Что называют нормалью к поверхности

в заданной точке ее?

8. Как построить нормаль к поверхности вра-

щения в данной точке ее?

ГЛАВА 11

ПОСТРОЕНИЕ РАЗВЕРТОК

( 57. РАЗВЕРТКИ МНОГОГРАННИКОВ

Разверткой многогранной поверхности

называется плоская фигура, получаемая

последовательным совмещением всех гра-

ней поверхности с одной плоскостью. Так

как все грани многогранной поверхности

изображаются на развертке в натураль-

ную величину, построение ее сводится к

определению величины отдельных граней

поверхности — плоских многоугольников.

1. Развертка пирамиды. Развертка пи-

рамиды осуществляется в следующем по-,

рядке:

а) определяют истинную величину всех

ребер пирамиды любым из известных спо-

собов. На рис. 293 способом вращения

найдена длина боковых ребер и способом

замены плоскостей проекций определено

основание пирамиды;

б) по найденным трем сторонам

(рис. 294) строят какую-либо из боковых

граней, например SoAoflo, пристраивая к

ней следующую SoBoCo, а затем и осталь-

ные грани (масштаб развертки уменьшен);

в) достраивают основание пирамиды

AoBoCoDo.

Точки, расположенные внутри контура

развертки, находятся во взаимно одноз-

начном соответствии с точками поверхно-

сти многогранника. Но каждой точке тех

ребер, по которым многогранник разрезан,

на развертке соответствуют две точки,

принадлежащие контуру развертки. При-

мером первой пары точек на рисунках слу-

жат точки Ко и K^SAD, а иллюстрацией

второго случая являются точки М и Мо.

Для определения точки Ко на развертке

пришлось по ее ортогональным проекциям

(рис. 293) найти длины отрезков AM (спо-

собом замены плоскостей проекций) и SK

(способом вращения). Эти отрезки и были

использованы затем при построении на

развертке сначала прямой SoMo и, нако-

нец, точки Ко-

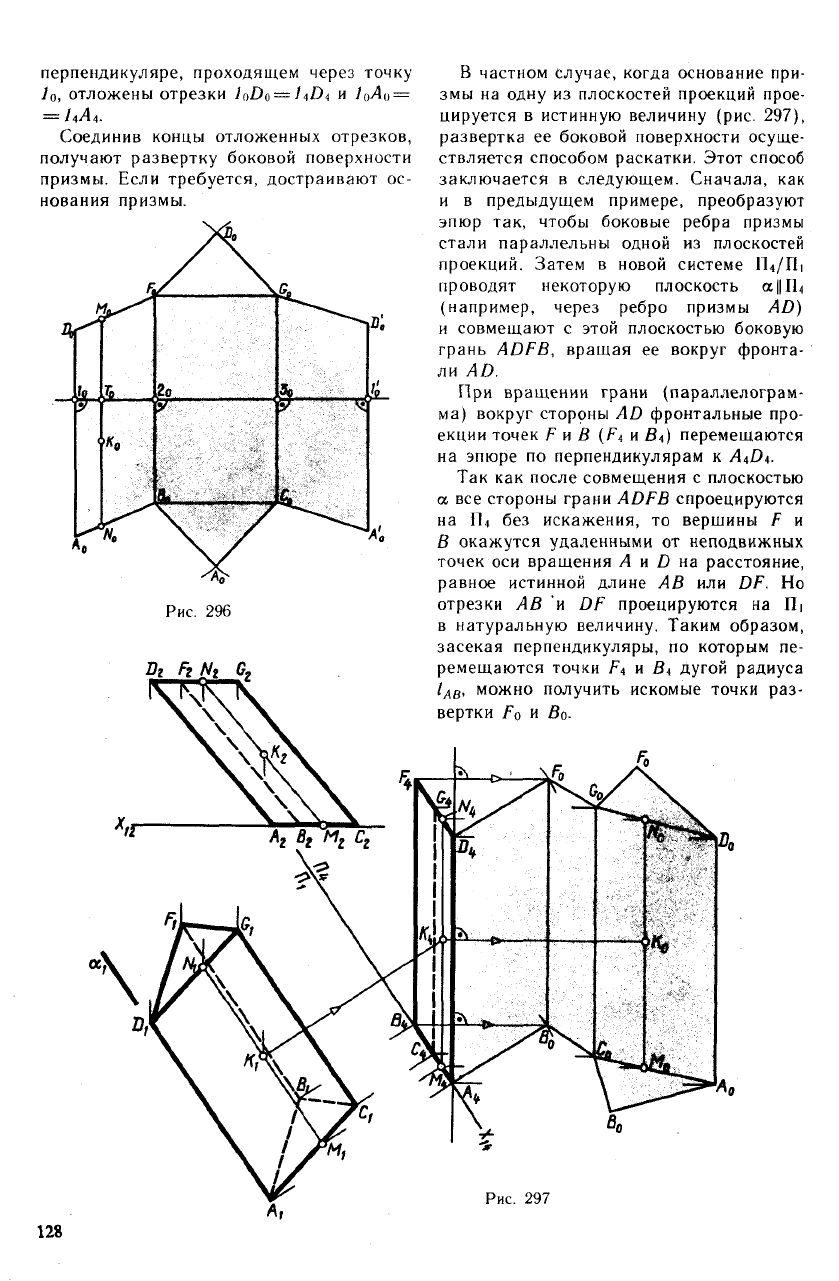
2. Развертка призмы. В общем случае

развертка призмы выполняется следую-

щим образом. Преобразуют эпюр так, что-

бы боковые ребра призмы стали парал-

лельны новой плоскости проекций (рис.

295). Тогда на эту плоскость (в данном

примере на П.») боковые ребра спроециру-

ются в истинную величину.

Пересекая призму вспомогательной

плоскостью а, перпендикулярной ее боко-

вым ребрам, строят проекции фигуры нор-

мального сечения — треугольника I, 2, 3,

а затем определяют истинную величину

этого сечения. На рис. 295 Она найдена

способом вращения.

126

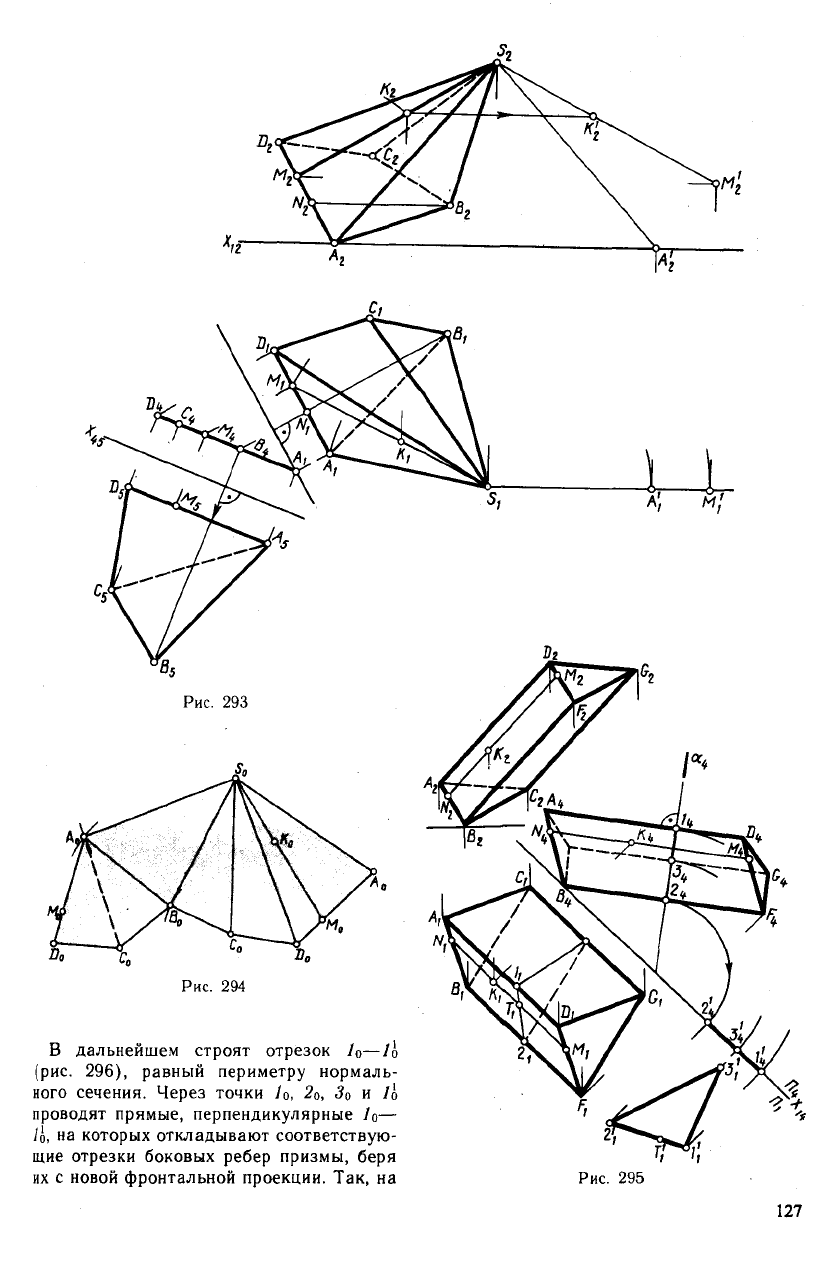
Рис. 293

A; Mj

Рис. 294

В дальнейшем строят отрезок /о—1

(рис. 296), равный периметру нормаль-

ного сечения. Через точки /о, 2

, ЗО и /о

проводят прямые, перпендикулярные 1 о—

1 о, на которых откладывают соответствую-

щие отрезки боковых ребер призмы, беря

их с новой фронтальной проекции. Так, на

Рис. 295

127

перпендикуляре, проходящем через точку

/о, отложены отрезки loDo — 14D4 и /оА> =

= 1

Соединив концы отложенных отрезков,

получают развертку боковой поверхности

призмы. Если требуется, достраивают ос-

нования призмы.

Рг Ft Nt G,

В частном случае, когда основание при-

змы на одну из плоскостей проекций прое-

цируется в истинную величину (рис. 297),

развертка ее боковой поверхности осуще-

ствляется способом раскатки. Этот способ

заключается в следующем. Сначала, как

и в предыдущем примере, преобразуют

эпюр так, чтобы боковые ребра призмы

стали параллельны одной из плоскостей

проекций. Затем в новой системе ГЦ/П,

проводят некоторую плоскость

ос || П4

(например, через ребро призмы AD)

и совмещают с этой плоскостью боковую

грань ADFB, вращая ее вокруг фронта-

ли AD.

При вращении грани (параллелограм-

ма) вокруг сторрны AD фронтальные про-

екции точек F и В (F4 и В

) перемещаются

на эпюре по перпендикулярам к A

D*.

Так как после совмещения с плоскостью

а все стороны грани ADFB спроецируются

на П

без искажения, то вершины F и

В окажутся удаленными от неподвижных

точек оси вращения А и D на расстояние,

равное истинной длине АВ или DF. Но

отрезки АВ и DF проецируются на П|

в натуральную величину. Таким образом,

засекая перпендикуляры, по которым пе-

ремещаются точки F4 и В\ дугой радиуса

Д8

, можно получить искомые точки раз-

вертки Fo и Во-

Рис. 300

128

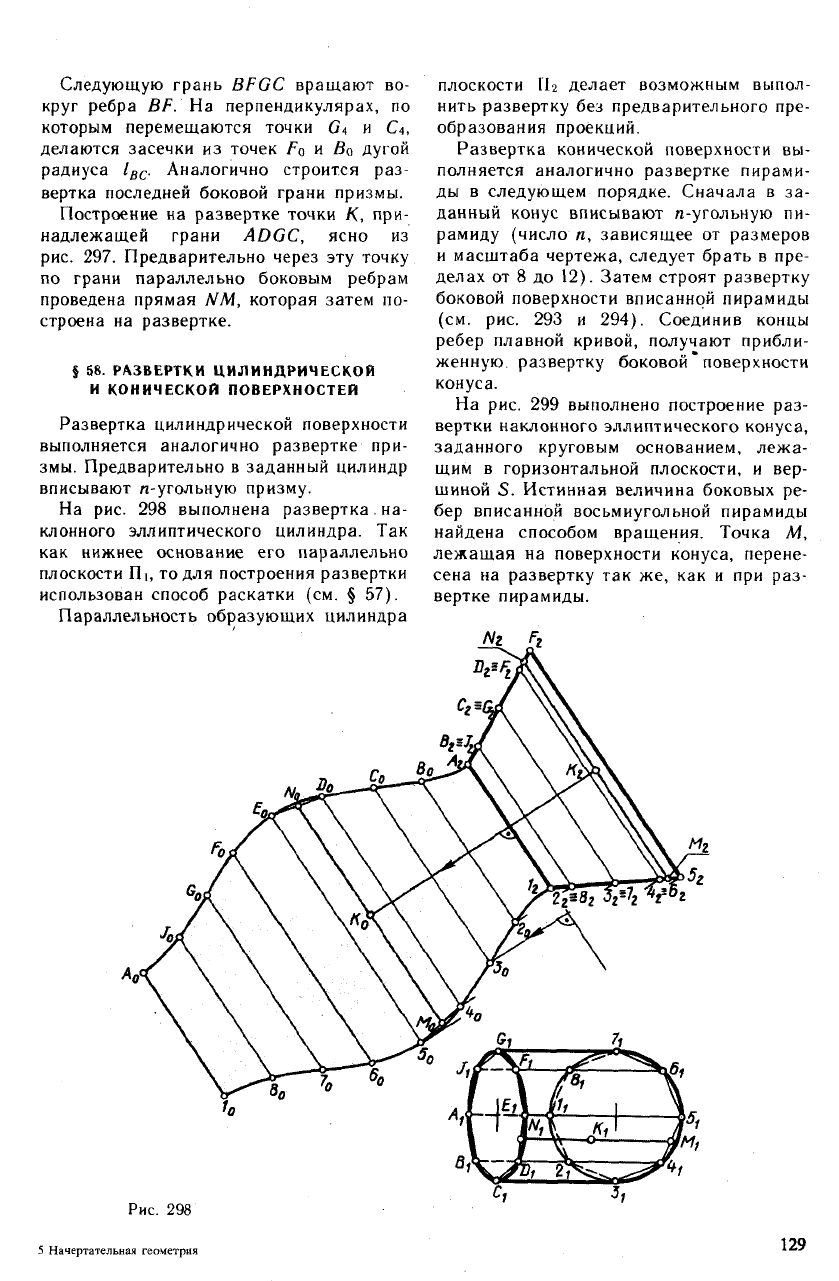
Следующую грань BFGC вращают во-

круг ребра BF. На перпендикулярах, по

которым перемещаются точки G4 и

делаются засечки из точек Fo и Во дугой

радиуса (

вс

. Аналогично строится раз-

вертка последней боковой грани призмы.

Построение на развертке точки К, при-

надлежащей грани ADGC, ясно из

рис. 297. Предварительно через эту точку

по грани параллельно боковым ребрам

проведена прямая NM, которая затем по-

строена на развертке.

§ 58. РАЗВЕРТКИ ЦИЛИНДРИЧЕСКОЙ

И КОНИЧЕСКОЙ ПОВЕРХНОСТЕЙ

Развертка цилиндрической поверхности

выполняется аналогично развертке при-

змы. Предварительно в заданный цилиндр

вписывают n-угольную призму.

На рис. 298 выполнена развертка . на-

клонного эллиптического цилиндра. Так

как нижнее основание его параллельно

плоскости Пь то для построения развертки

использован способ раскатки (см. § 57).

Параллельность образующих цилиндра

плоскости Г1г делает возможным выпол-

нить развертку без предварительного пре-

образования проекций.

Развертка конической поверхности вы-

полняется аналогично развертке пирами-

ды в следующем порядке. Сначала в за-

данный конус вписывают n-угольную пи-

рамиду (число я, зависящее от размеров

и масштаба чертежа, следует брать в пре-

делах от 8 до 12). Затем строят развертку

боковой поверхности вписанной пирамиды

(см. рис. 293 и 294). Соединив концы

ребер плавной кривой, получают прибли-

женную. развертку боковой поверхности

конуса.

На рис. 299 выполнено построение раз-

вертки наклонного эллиптического конуса,

заданного круговым основанием, лежа-

щим в горизонтальной плоскости, и вер-

шиной S. Истинная величина боковых ре-

бер вписанной восьмиугольной пирамиды

найдена способом вращения. Точка М,

лежащая на поверхности конуса, перене-

сена на развертку так же, как и при раз-

вертке пирамиды.

Рис. 298

5 Начертательная геометрия

129