Крылов Н.Н., ред. Начертательная геометрия

Подождите немного. Документ загружается.

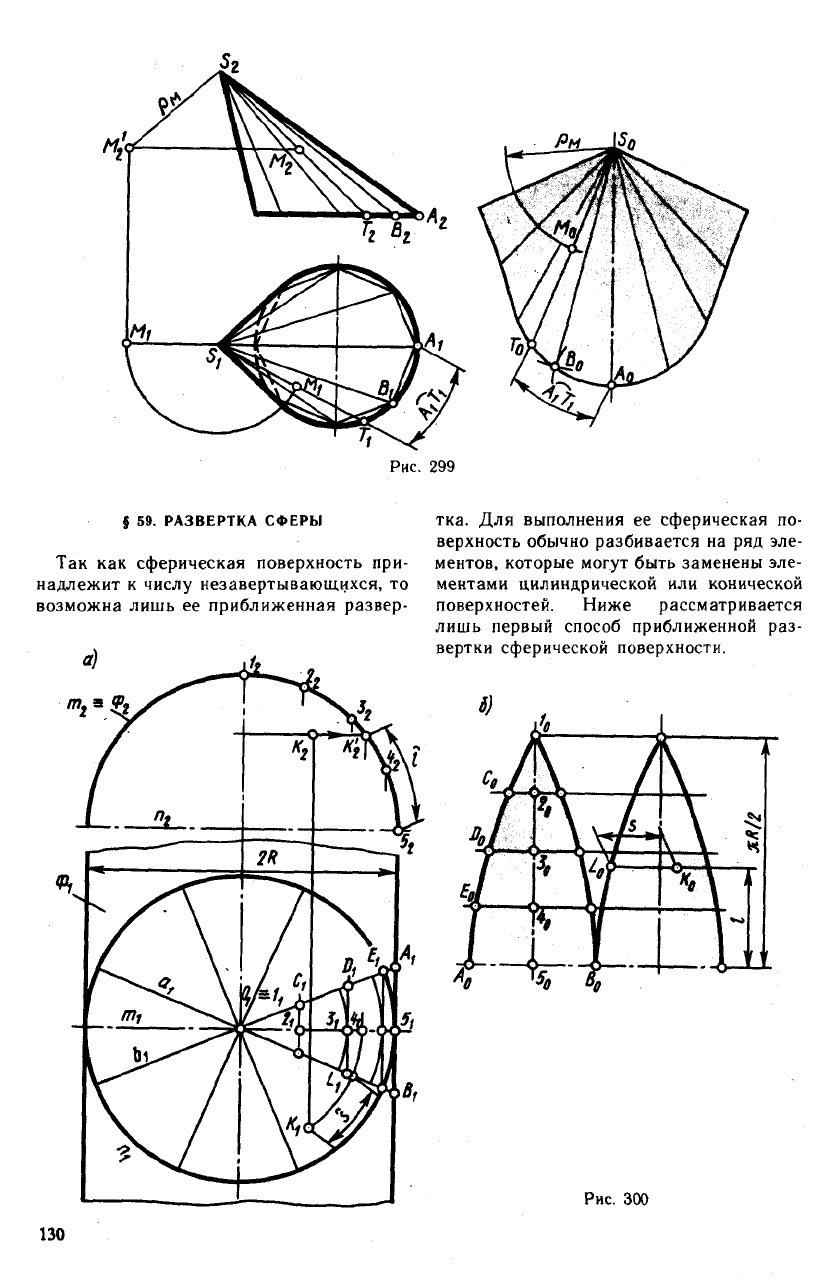
Рис. 299

§ 59. РАЗВЕРТКА СФЕРЫ

Так как сферическая поверхность при-

надлежит к числу незавертывающихся, то

возможна лишь ее приближенная развер-

тка. Для выполнения ее сферическая по-

верхность обычно разбивается на ряд эле-

ментов, которые могут быть заменены эле-

ментами цилиндрической или конической

поверхностей. Ниже рассматривается

лишь первый способ приближенной раз-

вертки сферической поверхности.

Рис. 300

130

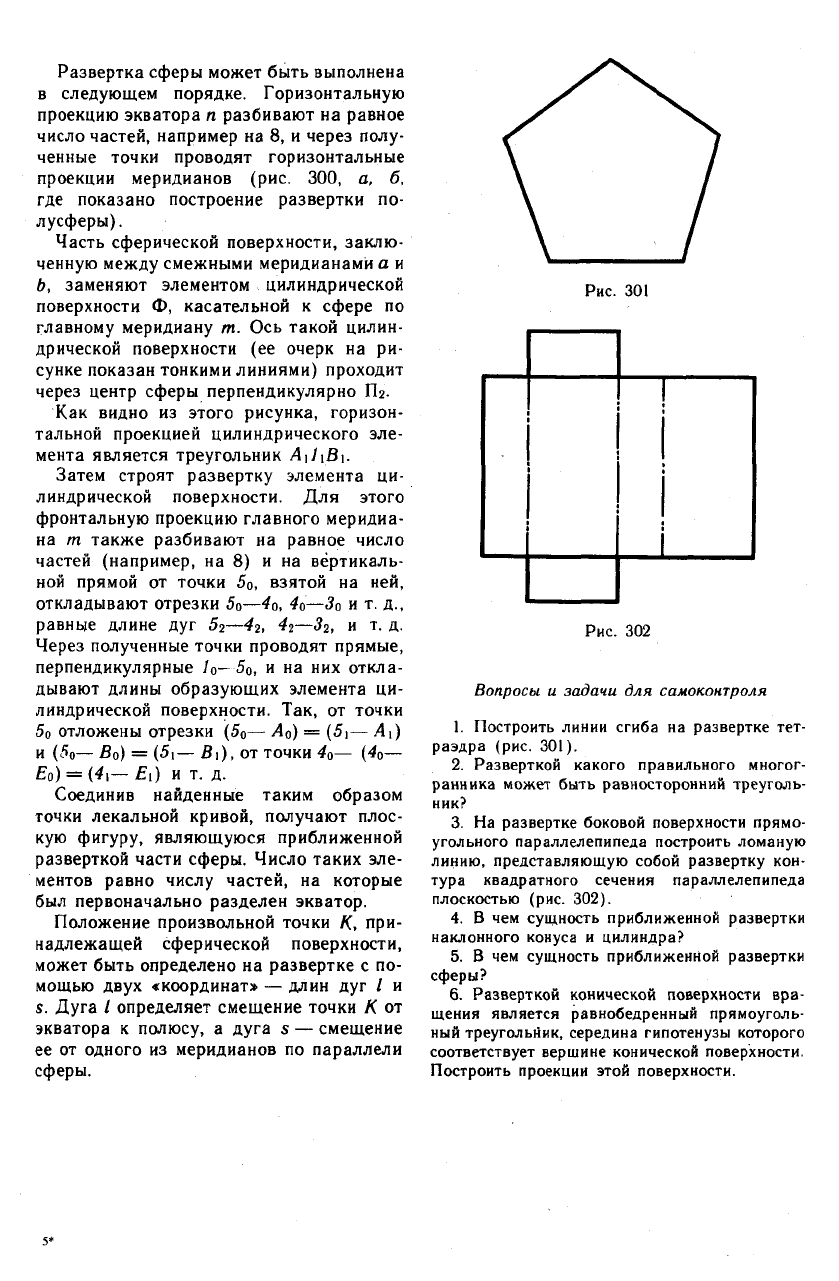
Развертка сферы может быть выполнена

в следующем порядке. Горизонтальную

проекцию экватора п разбивают на равное

число частей, например на 8, и через полу-

ченные точки проводят горизонтальные

проекции меридианов (рис. 300, а, б,

где показано построение развертки по-

лусферы).

Часть сферической поверхности, заклю-

ченную между смежными меридианами а и

Ь, заменяют элементом цилиндрической

поверхности Ф, касательной к сфере по

главному меридиану т. Ось такой цилин-

дрической поверхности (ее очерк на ри-

сунке показан тонкими линиями) проходит

через центр сферы перпендикулярно Пг.

Как видно из этого рисунка, горизон-

тальной проекцией цилиндрического эле-

мента является треугольник А\1\В\.

Затем строят развертку элемента ци-

линдрической поверхности. Для этого

фронтальную проекцию главного меридиа-

на т также разбивают на равное число

частей (например, на 8) и на вертикаль-

ной прямой от точки 5о, взятой на ней,

откладывают отрезки 5о—4о, 4о—Зо и т. д.,

равные длине дуг 5

—4

, 4

—3

, и т. д.

Через полученные точки проводят прямые,

перпендикулярные /о— 5о, и на них откла-

дывают длины образующих элемента ци-

линдрической поверхности. Так, от точки

5о отложены отрезки (5о— Ао) = (51— j4i)

и (5о— Во) = (5i— В]), от точки 4

— (4

—

Ео) = (41— Ei) и т. д.

Соединив найденные таким образом

точки лекальной кривой, получают плос-

кую фигуру, являющуюся приближенной

разверткой части сферы. Число таких эле-

ментов равно числу частей, на которые

был первоначально разделен экватор.

Положение произвольной точки К, при-

надлежащей сферической поверхности,

может быть определено на развертке с по-

мощью двух «координат» — длин дуг I и

s. Дуга / определяет смещение точки К от

экватора к полюсу, а дуга s — смещение

ее от одного из меридианов по параллели

сферы.

Рис. 302

Вопросы и задачи для самоконтроля

1. Построить линии сгиба на развертке тет-

раэдра (рис. 301).

2. Разверткой какого правильного многог-

ранника может быть равносторонний треуголь-

ник?

3. На развертке боковой поверхности прямо-

угольного параллелепипеда построить ломаную

линию, представляющую собой развертку кон-

тура квадратного сечения параллелепипеда

плоскостью (рис. 302).

4. В чем сущность приближенной развертки

наклонного конуса и цилиндра?

5. В чем сущность приближенной развертки

сферы?

6. Разверткой конической поверхности вра-

щения является равнобедренный прямоуголь-

ный треугольник, середина гипотенузы которого

соответствует вершине конической поверхности.

Построить проекции этой поверхности.

РАЗДЕЛ 2

ПРОЕКЦИИ АКСОНОМЕТРИЧЕСКИЕ, ПЕРСПЕКТИВНЫЕ

И С ЧИСЛОВЫМИ ОТМЕТКАМИ

ГЛАВА 12

МЕТОД ПАРАЛЛЕЛЬНОГО

ПРОЕЦИРОВАНИЯ НА ОДНУ

ПЛОСКОСТЬ (АКСОНОМЕТРИЯ)

§ 60. СУЩНОСТЬ МЕТОДА

И ОСНОВНЫЕ понятия

Аксонометрические изображения широ-

ко применяются благодаря хорошей на-

глядности и простоте построений.

Слово «аксонометрия» в переводе с гре-

ческого означает измерение по осям. Аксо-

нометрический метод может сочетаться

и с параллельным, и с центральным прое-

цированием при условии, что предмет про-

ецируется вместе с координатной систе-

мой.

Сущность метода параллельного аксо-

нометрического проецирования заключа-

ется в том,

что

предмет относят к некото-

рой системе координат и затем проециру-

ют параллельными лучами на плоскость

вместе с координатной системой.

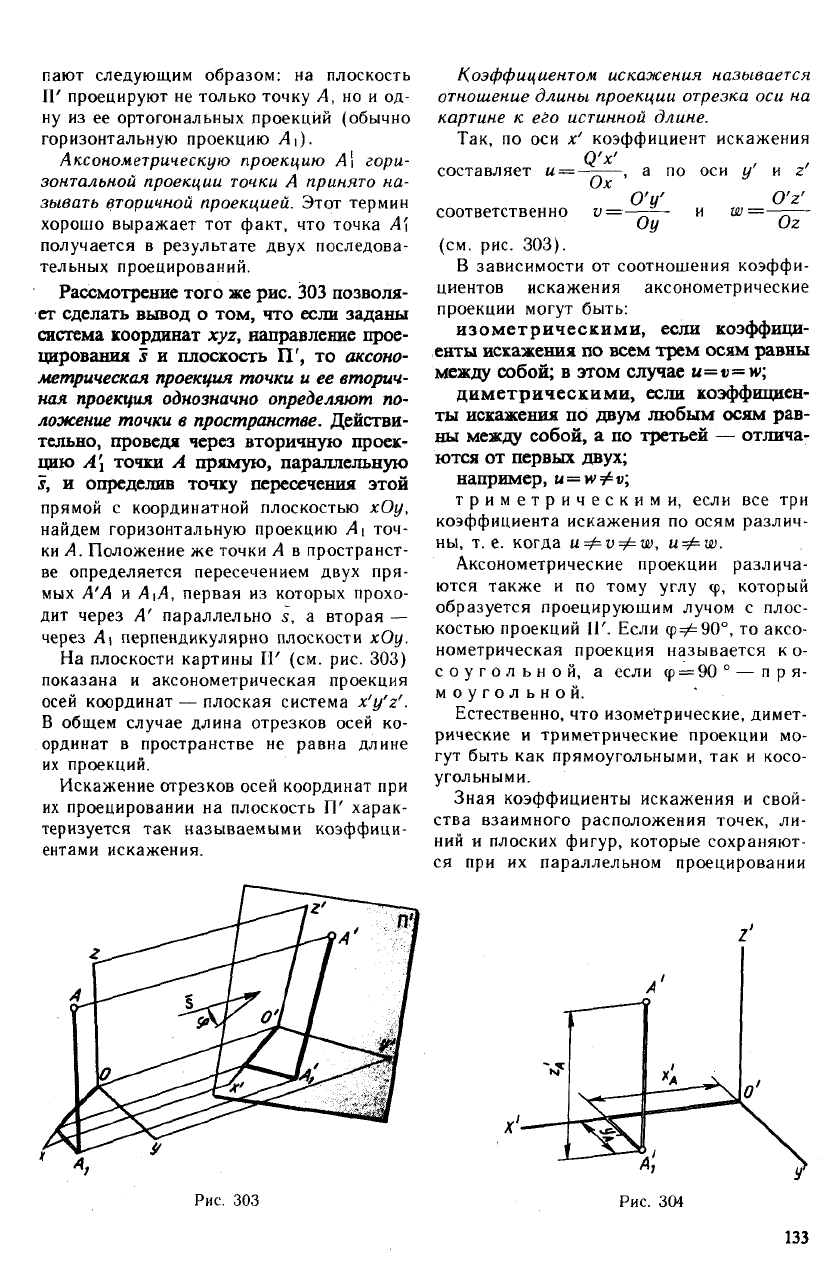
На рис. 303 показана точка А, отнесен-

ная к системе прямоугольных координат

xyz.

Вектор s определяет направление прое-

цирования на картинную плоскость П'

(плоскость проекций).

Для создания аксонометрической * (в

нашем случае параллельной) проекции

точки А проведем через нее проецирую-

щий луч (параллельный вектору s) и най-

дем пересечение его с плоскостью П' в точ-

ке А'. Это построение показывает, что

при заданном направлении проецирования

каждой точке А пространства на плоско-

сти проекций соответствует определенная

точка А'.

Но обратное, как известно, утверждать

нельзя. Действительно, каждой точке А!

на плоскости ГГ соответствует любая точ-

ка проецирующего луча А'А.

Для того чтобы устранить эту неопреде-

ленность и обеспечить взаимную одно-

значность между точками пространст-

ва и точками картинной плоскости, посту-

* В дальнейшем параллельную проекцию бу-

дем называть аксонометрической, помня, одна-

ко, о том, что аксонометрическая проекция мо-

жет быть и центральной.

132

пают следующим образом: на плоскость

1Г проецируют не только точку Л, но и од-

ну из ее ортогональных проекцйй (обычно

горизонтальную проекцию А|).

Аксонометрическую проекцию АI гори-

зонтальной проекции точки А принято на-

зывать вторичной проекцией. Этот термин

хорошо выражает тот факт, что точка А\

получается в результате двух последова-

тельных проецирований.

Рассмотрение того же рис. 303 позволя-

ет сделать вывод о том, что если заданы

система координат xyz, направление прое-

цирования s и плоскость П', то аксоно-

метрическая проекция точки и ее вторич-

ная проекция однозначно определяют по-

ложение точки в пространстве. Действи-

тельно, проведя через вторичную проек-

цию А\ точки А прямую, параллельную

s, и определив точку пересечения этой

прямой с координатной плоскостью хОу,

найдем горизонтальную проекцию А\ точ-

ки А. Положение же точки А в пространст-

ве определяется пересечением двух пря-

мых А'А и А\А, первая из которых прохо-

дит через А' параллельно s, а вторая —

через А\ перпендикулярно плоскости хОу.

На плоскости картины ГГ (см. рис. 303)

показана и аксонометрическая проекция

осей координат — плоская система x'y'z'.

В общем случае длина отрезков осей ко-

ординат в пространстве не равна длине

их проекций.

Искажение отрезков осей координат при

их проецировании на плоскость П' харак-

теризуется так называемыми коэффици-

ентами искажения.

Коэффициентом искажения называется

отношение длины проекции отрезка оси на

картине к его истинной длине.

Так, по оси х' коэффициент искажения

О'х'

составляет и=———, а по оси у' и z'

Ох

О'у' O'z'

соответственно v= „ и ш=—-—

Оу Oz

(см. рис. 303).

В зависимости от соотношения коэффи-

циентов искажения аксонометрические

проекции могут быть:

изометрическими, если коэффици-

енты искажения по всем трем осям равны

между собой; в этом случае u=v=w;

диметрическими, если коэффициен-

ты искажения по двум любым осям рав-

ны между собой, а по третьей — отлича-

ются от первых двух;

например, u=w¥

триметрическими, если все три

коэффициента искажения по осям различ-

ны, т.е. когда ифиф-w, иФ-w.

Аксонометрические проекции различа-

ются также и по тому углу (р, который

образуется проецирующим лучом с плос-

костью проекций II'. Если ф=^90°, то аксо-

нометрическая проекция называется к о-

соугольной, а если

= 90°—пря-

моугольной.

Естественно, что изометрические, димет-

рические и триметрические проекции мо-

гут быть как прямоугольными, так и косо-

угольными.

Зная коэффициенты искажения и свой-

ства взаимного расположения точек, ли-

ний и плоских фигур, которые сохраняют-

ся при их параллельном проецировании

133

(см. § 3), можно построить аксонометри-

ческое изображение точки А. Это изобра-

жение определяется как граничная точка

координатной ломаной, состоящей из от-

резков длиной Х'А, У'А, Z'A, отложенных от

начала аксонометрических осей О' на со-

ответствующих прямых, параллельных

этим осям (рис. 304) или совпадающих

с ними.

Построение координатной ломаной тре-

бует измерения трех прямоугольных" ко-

ординат х, у, z точки перевода их при

помощи коэффицентов искажения в аксо-

нометрические и, наконец, вычерчивания

этой ломаной, при построении которой по-

путно строится и одна из вторичных проек-

ций точки.

$ 61. ОСНОВНАЯ ТЕОРЕМА АКСОНОМЕТРИИ

При построении параллельной проекции

можно произвольно выбрать плоскость

проекций ГГ и направление проецирова-

ния.

Очевидно, любое изменение взаимного

положения осей координат и плоскости

проекций и всякое изменение направления

проецирования вызовет как изменение по-

ложения аксонометрических осей, так и

коэффициентов искажения по ним.

Геометр, прошлого века К. Польке в

1853 г., изучая вопрос о том, в какой

зависимости находятся направления аксо-

нометрических осей и коэффициенты иска-

жения по ним от направления проецирова-

ния и положения плоскости проекций, при-

шел к следующему выводу:

три

произволь-

но выбранных отрезка О'х', О'у', O'z'

(см. рис. 303) на плоскости П', выходя-

щие из одной точки, представляют парал-

лельную проекцию трех равных и взаимно

перпендикулярных отрезков Ох, Оу, Ог,

выходящих из некоторой точки простран-

ства *.

Эта теорема К. Польке имеет сущес-

твенное значение как для теории аксоно-

метрии, так и для многих ее приложений.

На. основании теоремы Польке системы

аксонометрических осей, а также отноше-

* Доказательство теоремы Польке см. в кн.:

Глазунов Е. А., Четверухин Н. Ф. Аксономет-

рия. М„ 1953.

ние коэффициентов искажения по ним мо-

гут быть заданы совершенно произвольно.

Коэффициенты искажения пропорцио-

нальны соответственно отрезкам, изобра-

жающим аксонометрические оси. Действи-

тельно, отрезки О'х', О'у' и O'z', которые

являются числителями дробей, определяю-

щих коэффициенты искажения и, v, w,

могут быть согласно теореме Польке

выбраны произвольно. Но все эти три

произвольно выбранных отрезка служат

параллельной проекцией трех равных и

взаимно перпендикулярных отрезков

пространства. Пусть длина каждого из

них равна т. Составив отношение

О'х' О'у' O'z'

u:v.w=~——: „ :——— и, заменяя Ох,

Ох Оу Oz

Оу, Ог через т, получим

u:v:w = 0'x':0'y':0'z',

что и доказывает пропорциональность ко-

эффициентов искажения соответствую-

щим отрезкам.

$ 62. ЗАВИСИМОСТЬ МЕЖДУ

КОЭФФИЦИЕНТАМИ ИСКАЖЕНИЯ

И УГЛОМ ПРОЕЦИРОВАНИЯ

Между коэффициентами искажения и

углом <р, образованным направлением про-

ецирования с плоскостью П', существует

следующая зависимость:

4V +

= 2 + ctg

cp. (12.1)

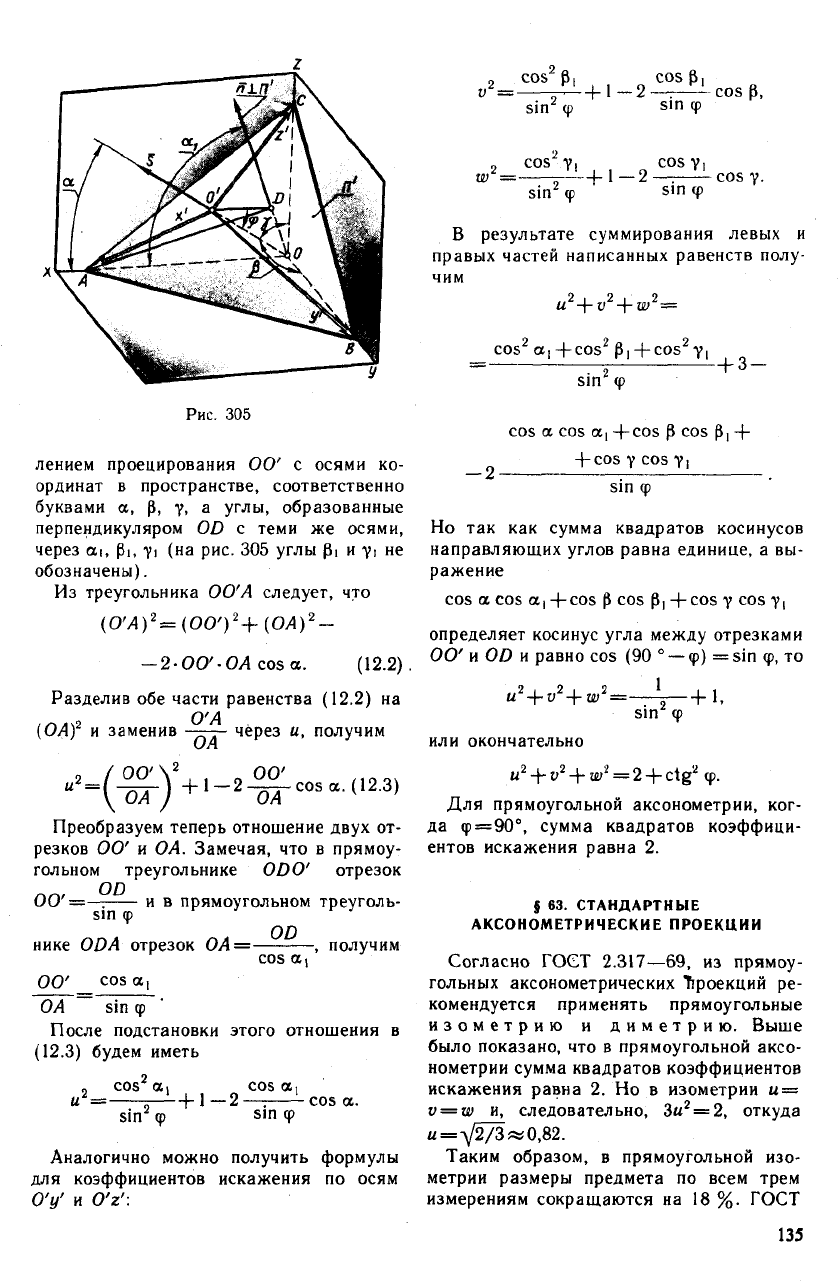
Для доказательства этого равенства об-

ратимся к рис. 305, на котором изображе-

ны прямоугольная система координат хуг

и плоскость аксонометрических проекций

П'. Направление проецирования задано

отрезком 00', причем точка О' является

проекцией начала координат О на плос-

кость П'.

Отрезки О'А, О'В и О'С представляют

собой аксонометрические оси координат.

Угол ф, который образует направление

проецирования с плоскостью проекций II',

измеряется углом OO'D. Сторона O'D это-

го угла служит ортогональной проекцией

направления проецирования 00' на плос-

кость П'. Точка D является, таким обра-

зом, основанием перпендикуляра, опущен-

ного из начала координат О на плоскость

проекций П'.

Обозначим углы, образованные направ-

134

—

•

00'

•

OA cos a.

(12.2)

Разделив обе части равенства (12.2) на

О'А

(OA) и заменив

через и, получим

+ 1-2

00'

cos a. (12.3)

Преобразуем теперь отношение двух от-

резков 00' и OA. Замечая, что в прямоу-

гольном треугольнике ODO' отрезок

пп/

ОО ——; и в прямоугольном треуголь-

sin

<р

нике ODA отрезок ОА=———, получим

cos a,

ОО' _ cos a,

OA sin qj

После подстановки этого отношения в

(12.3) будем иметь

cos a

sin

COS «1

-2—- cos a.

sin ф

Аналогично можно получить формулы

для коэффициентов искажения по осям

О'у' и O'z'.

cos

p, cosp,

1- 1 —2 —: COS P,

- Sin ф

—

Sin ф

cos

VI , , _ COSY,

W = S 1- 1 —2 —

COS Y.

Sin ф

В результате суммирования левых и

правых частей написанных равенств полу-

чим

+1/

+ш

cos

<Х|

+COS

PI + COS

+ 3-

Рис. 305

лением проецирования ОО' с осями ко-

ординат в пространстве, соответственно

буквами а, р, у, а углы, образованные

перпендикуляром OD с теми же осями,

через он, Pi, YI (на рис. 305 углы Pi и Yi не

обозначены).

Из треугольника ОО'А следует, что

(0'А)

=(00')

+ (ОА)

Sin ф

cos a cos a, +cos p cos p,

-j-cos y cos Yi

sin ф

-2

Но так как сумма квадратов косинусов

направляющих углов равна единице, а вы-

ражение

cos a cos a, +cos р cos р, +cos у cos Yi

определяет косинус угла между отрезками

ОО' и OD и равно cos (90 ° —ф) =sin ф, то

+ 1.

Sin ф

или окончательно

-)- у

+ до

= 2 -)- ctg

ф.

Для прямоугольной аксонометрии, ког-

да

= 90°, сумма квадратов коэффици-

ентов искажения равна 2.

§ 63. СТАНДАРТНЫЕ

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

Согласно ГОСТ 2.317—69, из прямоу-

гольных аксонометрических Проекций ре-

комендуется применять прямоугольные

изометрию и диметрию. Выше

было показано, что в прямоугольной аксо-

нометрии сумма квадратов коэффициентов

искажения равна 2. Но в изометрии ц =

v = w и, следовательно, Зи

= 2, откуда

= У273«0,82.

Таким образом, в прямоугольной изо-

метрии размеры предмета по всем трем

измерениям сокращаются на 18 %. ГОСТ

135

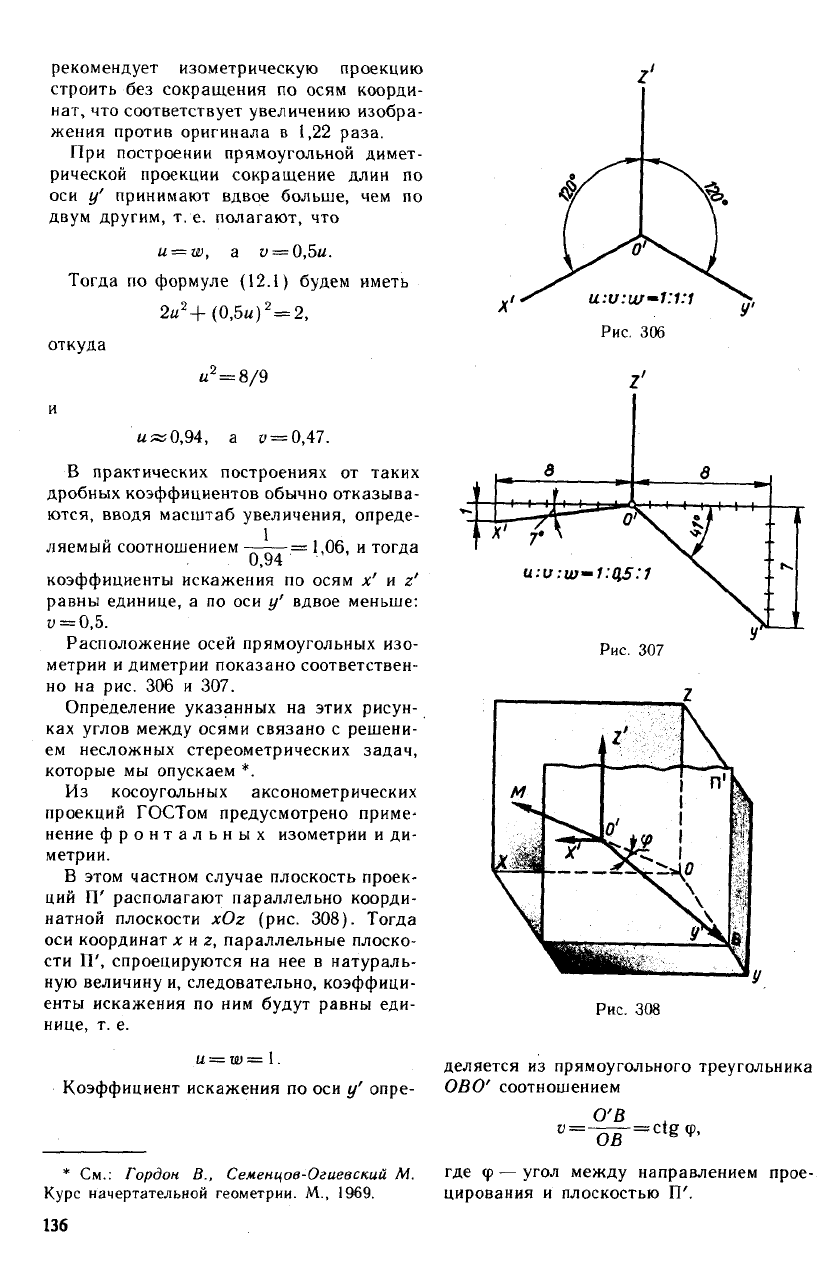
рекомендует изометрическую проекцию

строить без сокращения по осям коорди-

нат, что соответствует увеличению изобра-

жения против оригинала в 1,22 раза.

При построении прямоугольной димет-

рической проекции сокращение длин по

оси у' принимают вдвое больше, чем по

двум другим, т. е. полагают, что

u = w, а у = 0,5 и.

Тогда по формуле (12.1) будем иметь

2 «

+ (0,5и)

= 2,

откуда

=8/9

и яг 0,94, а у = 0,47.

В практических построениях от таких

дробных коэффициентов обычно отказыва-

ются, вводя масштаб увеличения, опреде-

ляемый соотношением —-= 1,06, и тогда

0,94

коэффициенты искажения по осям и z'

равны единице, а по оси у' вдвое меньше:

у = 0,5.

Расположение осей прямоугольных изо-

метрии и диметрии показано соответствен-

но на рис. 306 и 307.

Определение указанных на этих рисун-

ках углов между осями связано с решени-

ем несложных стереометрических задач,

которые мы опускаем *.

Из косоугольных аксонометрических

проекций ГОСТом предусмотрено приме-

нение фронтальных изометрии и ди-

метрии.

В этом частном случае плоскость проек-

ций П' располагают параллельно коорди-

натной плоскости xOz (рис. 308). Тогда

оси координат лиг, параллельные плоско-

сти П', спроецируются на нее в натураль-

ную величину и, следовательно, коэффици-

енты искажения по ним будут равны еди-

нице, т. е.

u = w= 1.

Коэффициент искажения по оси у' опре-

* См.: Гордон В., Семенцов-Огиевский М.

Курс начертательной геометрии. М., 1969.

деляется из прямоугольного треугольника

ОВО' соотношением

О'В

=ctg<p,

где

<р

— угол между направлением прое-

цирования и плоскостью П'.

136

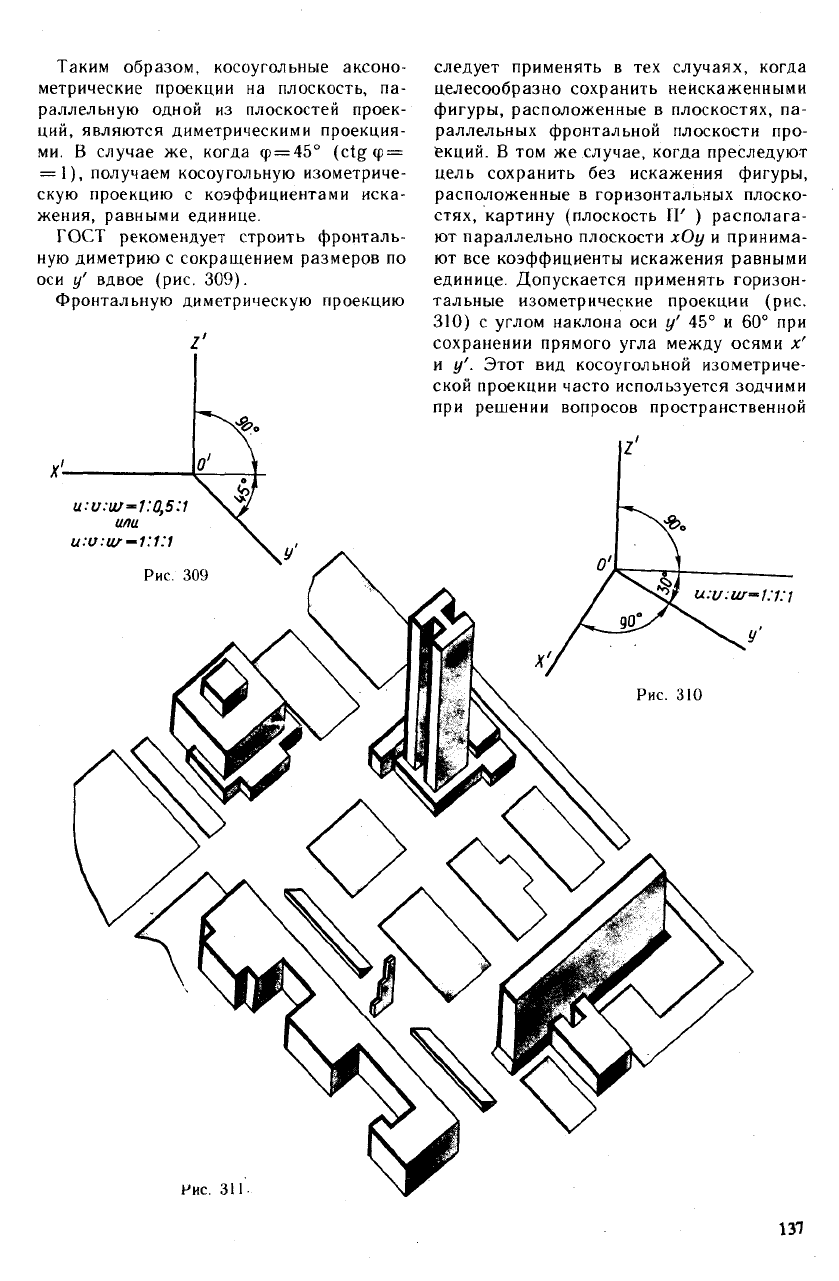
Таким образом, косоугольные аксоно-

метрические проекции на плоскость, па-

раллельную одной из плоскостей проек-

ций, являются диметрическими проекция-

ми. В случае же, когда

= 45° (ctg9 =

= 1), получаем косоугольную изометриче-

скую проекцию с коэффициентами иска-

жения, равными единице.

ГОСТ рекомендует строить фронталь-

ную диметрию с сокращением размеров по

оси у' вдвое (рис. 309).

Фронтальную диметрическую проекцию

и:и:Ш~Г.0,5:1

una

и:и:и/-1:1.1

Рис. 309

следует применять в тех случаях, когда

целесообразно сохранить неискаженными

фигуры, расположенные в плоскостях, па-

раллельных фронтальной плоскости про-

екций. В том же случае, когда преследуют

цель сохранить без искажения фигуры,

расположенные в горизонтальных плоско-

стях, картину (плоскость ГГ ) располага-

ют параллельно плоскости хОу и принима-

ют все коэффициенты искажения равными

единице. Допускается применять горизон-

тальные изометрические проекции (рис.

310) с углом наклона оси у' 45° и 60° при

сохранении прямого угла между осями х'

и у'. Этот вид косоугольной изометриче-

ской проекции часто используется зодчими

при решении вопросов пространственной

137

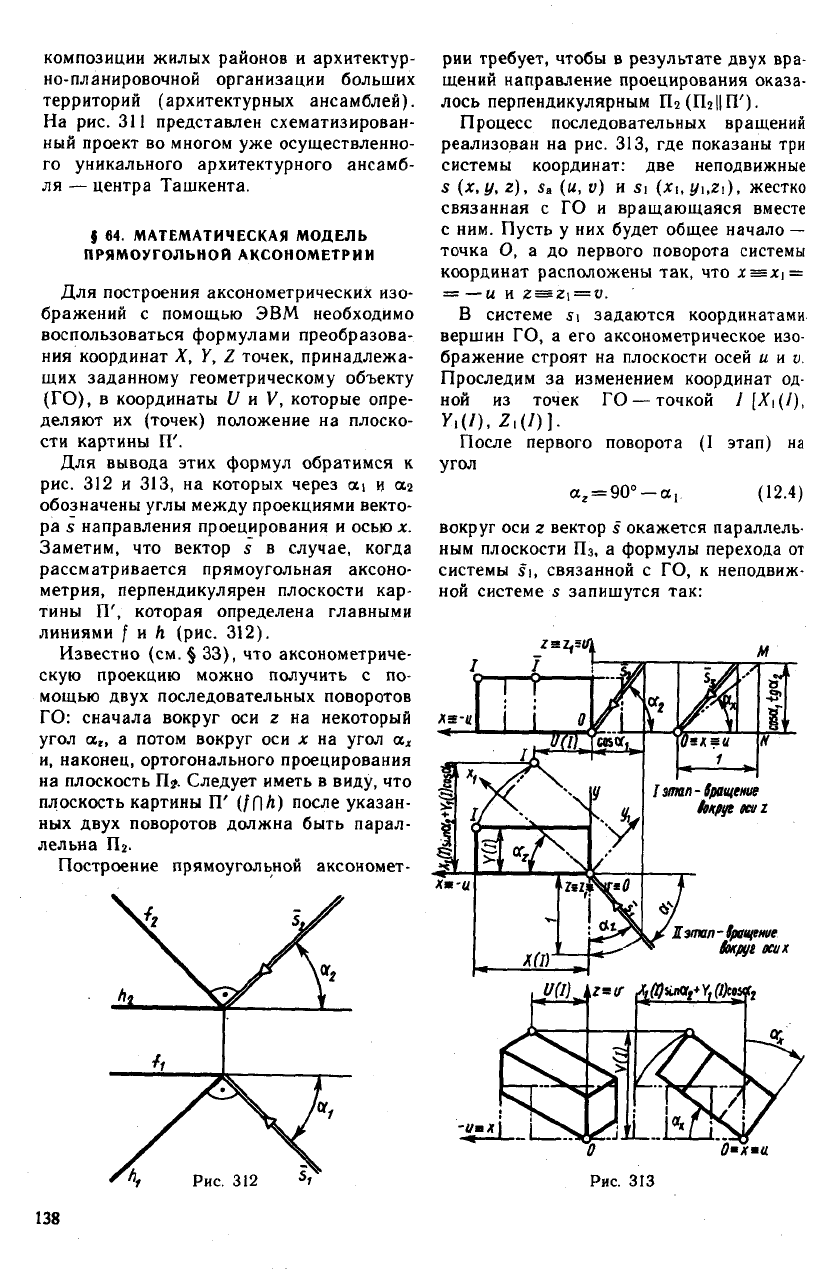
композиции жилых районов и архитектур-

но-планировочной организации больших

территорий (архитектурных ансамблей).

На рис. 311 представлен схематизирован-

ный проект во многом уже осуществленно-

го уникального архитектурного ансамб-

ля — центра Ташкента.

{ «4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

ПРЯМОУГОЛЬНОЙ АКСОНОМЕТРИИ

Для построения аксонометрических изо-

бражений с помощью ЭВМ необходимо

воспользоваться формулами преобразова-

ния координат X, Y, 2 точек, принадлежа-

щих заданному геометрическому объекту

(ГО), в координаты U и V, которые опре-

деляют их (точек) положение на плоско-

сти картины ГГ.

Для вывода этих формул обратимся к

рис. 312 и 313, на которых через он и а

обозначены углы между проекциями векто-

ра s направления проецирования и осью*.

Заметим, что вектор s в случае, когда

рассматривается прямоугольная аксоно-

метрия, перпендикулярен плоскости кар-

тины ГГ, которая определена главными

линиями / и h (рис. 312).

Известно (см. § 33), что аксонометриче-

скую проекцию можно получить с по-

мощью двух последовательных поворотов

ГО: сначала вокруг оси г на некоторый

угол а

, а потом вокруг оси х на угол а

и, наконец, ортогонального проецирования

на плоскость П?. Следует иметь в виду, что

плоскость картины П' (ff]h) после указан-

ных двух поворотов должна быть парал-

лельна Пг.

Построение прямоугольной аксономет-

138

рии требует, чтобы в результате двух вра-

щений направление проецирования оказа-

лось перпендикулярным П

(П

|! П').

Процесс последовательных вращений

реализован на рис. 313, где показаны три

системы координат: две неподвижные

s (х, у, 2), 5А (и, V) и si (Xi, </I,ZI), жестко

связанная с ГО и вращающаяся вместе

с ним. Пусть у них будет общее начало —

точка О, а до первого поворота системы

координат расположены так, что х==х\ =

— —

И Z = ZI = 0.

В системе si задаются координатами

вершин ГО, а его аксонометрическое изо-

бражение строят на плоскости осей инь.

Проследим за изменением координат од-

ной из точек ГО — точкой / [Xi(/),

У.</), -Z,(/)].

После первого поворота (I этап) на

угол

= 90° — а, (12.4)

вокруг оси z вектор s окажется параллель-

ным плоскости Пз, а формулы перехода от

системы si, связанной с ГО, к неподвиж-

ной системе s запишутся так:

= Xi (/) cos а

— Vi (/) sin а

;

Y = X\(I) sin а

(I) cos а

;

Z = Zi (/).

(12.5)

В результате второго вращения

(II этап) вокруг оси х на угол а

вектор

s станет перпендикулярным плоскости 1Ь.

Величину угла а

находим из треугольни-

ка OMN, в котором

tg a

= cos a, tg а

. (12.6)

Для вычисления «аксонометрических»

координат следует воспользоваться

формулами вида:

U (/) = -X, (/) cos а

+ V, (/) sin а

V (/)=[*, (/) sina

+y, (/) X

Xcos a J sin <x

-\-Z

(/) cos a

(12.7)

Формулы (12.7), описывающие линей-

ные преобразования, используются в даль-

нейшем (см. гл. 18) при составлении про-

граммы, реализующей машинное построе-

ние аксонометрических проекций.

Легко убедиться, что для прямоуголь-

ной изометрии ai = a2 = 45°. Для этого

достаточно точке А (1, 1,0) поставить в

соответствие точку А' на картине П' с ко-

ординатами U = 0, V = 0,82 и решить сис-

тему уравнений (12.7) относительно а

и а

, а затем определить ai и аг, используя

равенства (12.4) и (12.6).

Математическая модель параллельного

проецирования позволяет построить

третью проекцию объекта по двум данным.

Так, вид слева можно получить при ai =

= 180° и а

= 0.

§ 65. ОКРУЖНОСТЬ В АКСОНОМЕТРИИ

При параллельном проецировании ок-

ружности на какую-нибудь плоскость ГГ

(см. рис. 176 и 314) получаем ее изобра-

жение в общем случае в виде эллипса.

Как бы ни была расположена плоскость

окружности, сначала целесообразно по-

строить параллелограмм А'В'C'D' — па-

раллельную проекцию квадрата ABCD,

описанного около данной окружности, а

затем с помощью восьми точек и восьми

касательных вписать в него эллипс.

Первые четыре из этих точек — середи-

ны сторон параллелограмма. Остальные

Рис. 314

точки расположены на диагоналях так, что

каждая из них делит полудиагональ в от-

ношении 3:7.

Действительно, на основании свойств

параллельного проецирования можно за-

писать, что

АЕ А'Е'

ЕО Е'О'

Но

АЕ

-л/2-

ЕО

а значит,

А'Е'

Е'О'

Из восьми касательных к эллипсу первые

четыре — это стороны параллелограмма, а

остальные — прямые, параллельные его

диагоналям. Так, касательная F'T' к эл-

липсу параллельна диагонали А'С'.

Объясняется это тем, что F'T' и А'С' явля-

ются проекциями двух параллельных пря-

мых FT и АС.

Графические построения, предшествую-

щие вычерчиванию самого эллипса, пока-

заны на рис. 315. Их целесообразно вы-

полнять в такой последовательности:

1) построить аксонометрическую проек-

цию квадрата — параллелограмм

A'B'C'D' и провести диагонали А'С' и

B'D'\

2) отметить середины сторон паралле-

лограмма — точки /', 2', 3' и 4'\

3) на отрезке /'—В', как на гипотенузе,

построить прямоугольный равнобедренный

треугольник l'LB'\

139